MANAJEMEN KUANTITATIF PROGRAMA LINEAR METODE PRIMAL DUAL PERTEMUAN

MANAJEMEN KUANTITATIF PROGRAMA LINEAR METODE PRIMAL DUAL PERTEMUAN KE 5

METODE PRIMAL DUAL Untuk penyelesaian type Program Linier yang: Fungsi Tujuan → Minimasi Fungsi Pembatas → semuanya bertanda ≥ Primal program asal adalah Fungsi Tujuan Minimasi dengan Fungsi Pembatas ≥, sedangkan Dual merupakan program pasangan nya dengan Fungsi Tujuan Maksimasi dengan Fungsi Pembatas ≤. Metode Primal Dual dpat diselesainakan dengan Simpleks Sederhana (dari program Dualnya) Akan diperoleh Nilai Bayangannya (Shadow Price) dari Program Dual yang merupakan jawaban dari Program Asalnya (program Primal) Pada Program Dual variabel nya menggunakan nama lain “w”

PERUBAHAN PRIMAL MENJADI DUAL PRIMAL DUAL Min Z = CX Max Z = BT W Pembatas AX ≥ B Pembatas ATW ≤ CT C = Koefisien fungsi tujuan CT = Pembatas Dual (tranpose dari C) X = Varriable keputusan Primal W = Variabel keputusan Dual A = Matriks koefisien fungsi pembatas AT = Transpose dari A B = Nilai ruas kanan (pembatas) Primal BT = Transpose dari B

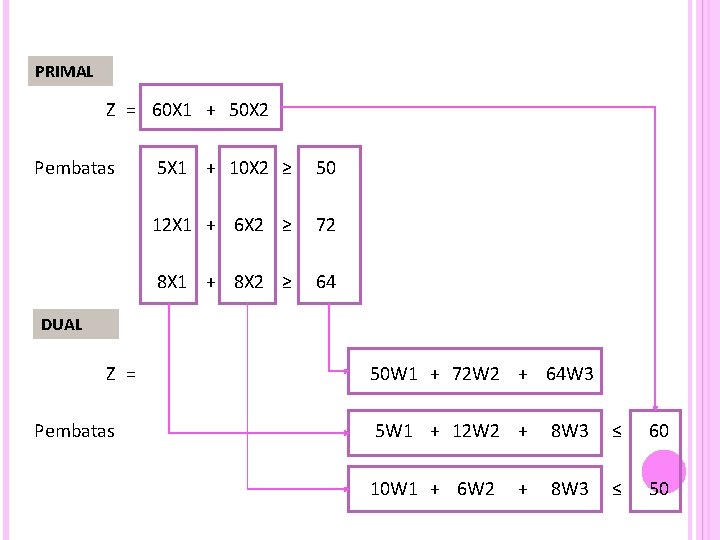
PRIMAL Z = 60 X 1 + 50 X 2 Pembatas 5 X 1 + 10 X 2 ≥ 12 X 1 + 6 X 2 ≥ 8 X 1 + 8 X 2 ≥ 50 72 64 DUAL Z = Pembatas 50 W 1 + 72 W 2 + 64 W 3 5 W 1 + 12 W 2 + 8 W 3 ≤ 10 W 1 + 6 W 2 8 W 3 ≤ + 60 50

CONTOH PRIMAL Max Z = 60 X 1+ S/t 5 X 1 + 12 X 1 + 8 X 1 + 50 X 2 10 X 2 ≥ 50 6 X 2 ≥ 72 8 X 2 ≥ 64 DUAL Min Z = 50 W 1 + 72 W 2 + 64 W 3 S/t 5 W 1 + 12 W 2 + 8 W 3 ≤ 60 10 W 1 + 6 W 2 + 8 W 3 ≤ 50 § Siapkan variabel baru, 3 variabel baru karena ada 3 pembatas § Program baru (dual) dengan 3 variabel dan 2 pembatas diselaikan dengan methode simpleks

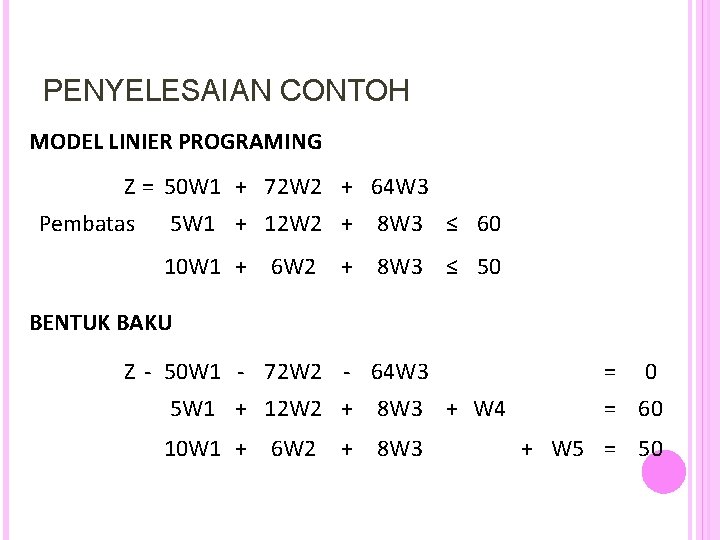
PENYELESAIAN CONTOH MODEL LINIER PROGRAMING Z = 50 W 1 + 72 W 2 + 64 W 3 Pembatas 5 W 1 + 12 W 2 + 8 W 3 ≤ 60 10 W 1 + 6 W 2 8 W 3 ≤ 50 + BENTUK BAKU Z - 50 W 1 - 72 W 2 - 64 W 3 5 W 1 + 12 W 2 + 8 W 3 + W 4 10 W 1 + 6 W 2 8 W 3 + = 0 = 60 + W 5 = 50

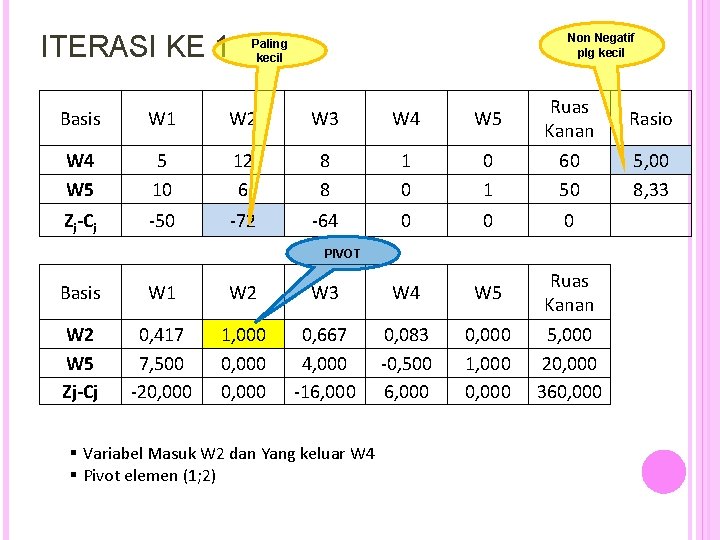
ITERASI KE 1 Non Negatif plg kecil Paling kecil Basis W 1 W 2 W 3 W 4 W 5 Ruas Kanan Rasio W 4 W 5 5 10 12 6 8 8 1 0 0 1 60 50 5, 00 8, 33 Zj-Cj -50 -72 -64 0 0 0 PIVOT Basis W 1 W 2 W 3 W 4 W 5 Ruas Kanan W 2 W 5 Zj-Cj 0, 417 7, 500 -20, 000 1, 000 0, 667 4, 000 -16, 000 0, 083 -0, 500 6, 000 0, 000 1, 000 0, 000 5, 000 20, 000 360, 000 § Variabel Masuk W 2 dan Yang keluar W 4 § Pivot elemen (1; 2)

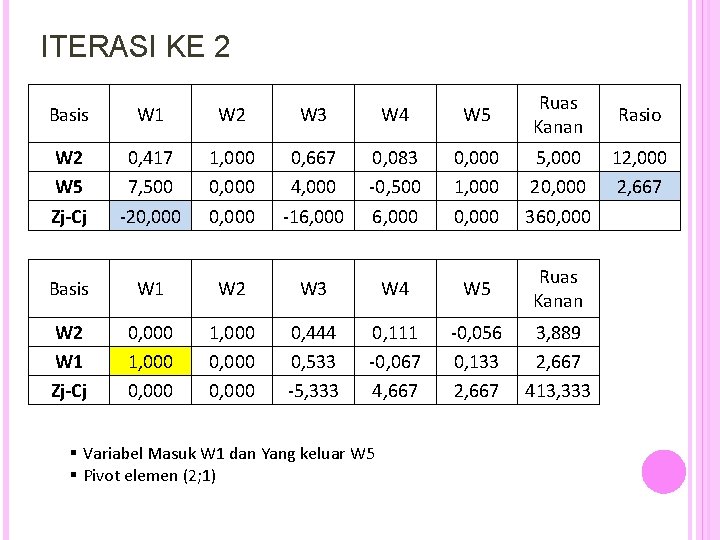
ITERASI KE 2 Basis W 1 W 2 W 3 W 4 W 5 Ruas Kanan Rasio W 2 W 5 Zj-Cj 0, 417 7, 500 -20, 000 1, 000 0, 667 4, 000 -16, 000 0, 083 -0, 500 6, 000 0, 000 1, 000 0, 000 5, 000 20, 000 360, 000 12, 000 2, 667 Basis W 1 W 2 W 3 W 4 W 5 Ruas Kanan W 2 W 1 Zj-Cj 0, 000 1, 000 0, 444 0, 533 -5, 333 0, 111 -0, 067 4, 667 -0, 056 0, 133 2, 667 3, 889 2, 667 413, 333 § Variabel Masuk W 1 dan Yang keluar W 5 § Pivot elemen (2; 1)

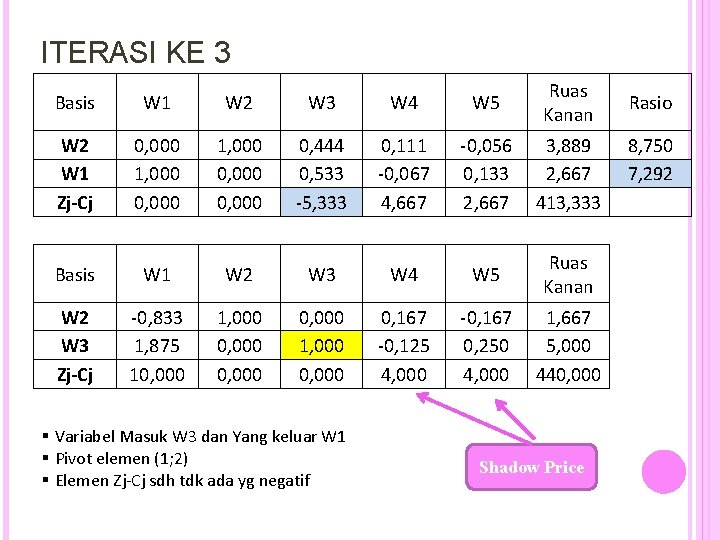
ITERASI KE 3 Basis W 1 W 2 W 3 W 4 W 5 Ruas Kanan Rasio W 2 W 1 Zj-Cj 0, 000 1, 000 0, 444 0, 533 -5, 333 0, 111 -0, 067 4, 667 -0, 056 0, 133 2, 667 3, 889 2, 667 413, 333 8, 750 7, 292 Basis W 1 W 2 W 3 W 4 W 5 Ruas Kanan W 2 W 3 Zj-Cj -0, 833 1, 875 10, 000 1, 000 0, 000 1, 000 0, 167 -0, 125 4, 000 -0, 167 0, 250 4, 000 1, 667 5, 000 440, 000 § Variabel Masuk W 3 dan Yang keluar W 1 § Pivot elemen (1; 2) § Elemen Zj-Cj sdh tdk ada yg negatif Shadow Price

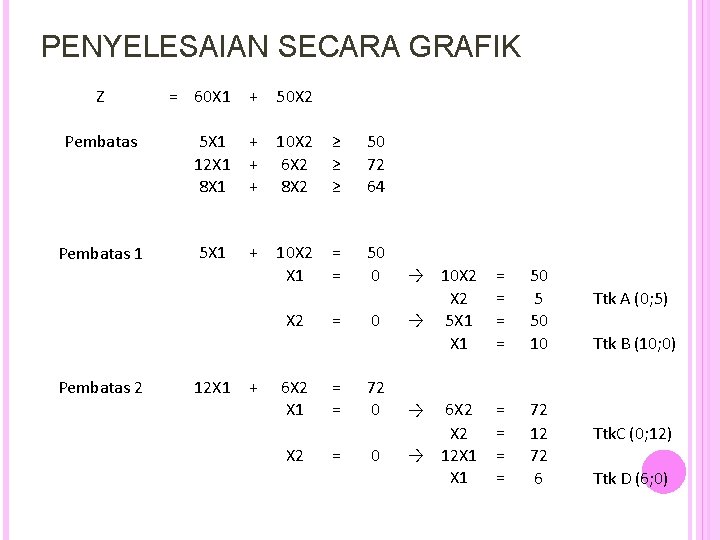
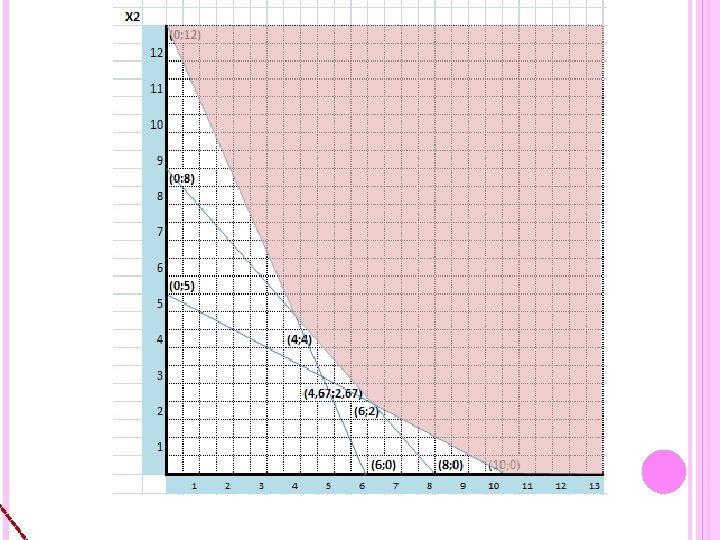
PENYELESAIAN SECARA GRAFIK Z Pembatas 1 = 60 X 1 + 50 X 2 5 X 1 + 12 X 1 + 8 X 1 + 10 X 2 6 X 2 8 X 2 ≥ ≥ ≥ 50 72 64 5 X 1 10 X 2 X 1 = = 50 0 + X 2 Pembatas 2 12 X 1 + 6 X 2 X 1 X 2 = = 0 72 0 0 → 10 X 2 → 5 X 1 = = 50 5 50 10 6 X 2 → 12 X 1 = = 72 12 72 6 → Ttk A (0; 5) Ttk B (10; 0) Ttk. C (0; 12) Ttk D (6; 0)

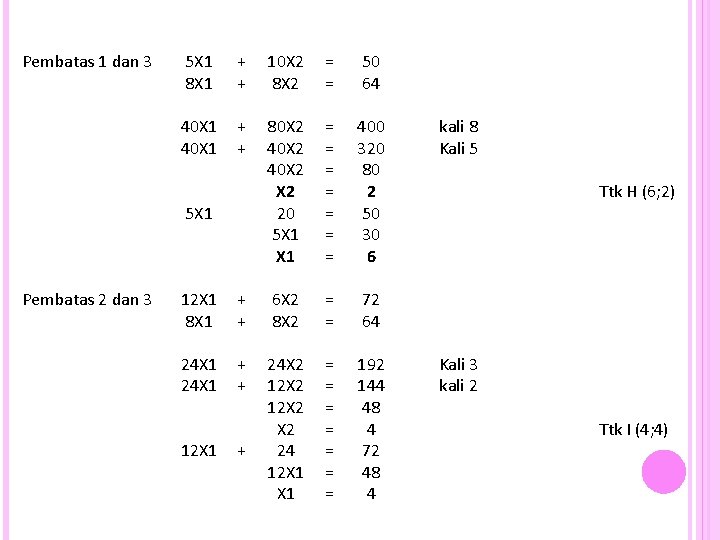
Pembatas 3 8 X 1 + 8 X 2 X 1 X 2 Pembatas 1 dan 2 5 X 1 12 X 1 + + 10 X 2 6 X 2 = = = 64 0 0 = = 50 72 60 X 1 + 120 X 2 = 60 X 1 + 30 X 2 = 90 X 2 = 600 360 240 X 2 5 X 1 = 2, 6667 + 26, 667 = 50 5 X 1 = 23, 333 = 4, 6667 X 1 → 8 X 2 → 8 X 1 = = 64 8 Ttk E (0; 8) Ttk F (8; 0) kali 12 Kali 5 Ttk G (4, 667; 2, 667)

Pembatas 1 dan 3 5 X 1 8 X 1 + + 10 X 2 8 X 2 = = 50 64 40 X 1 + + 80 X 2 40 X 2 20 5 X 1 = = = = 400 320 80 2 50 30 6 5 X 1 Pembatas 2 dan 3 12 X 1 8 X 1 + + 6 X 2 8 X 2 = = 72 64 24 X 1 + + 24 X 2 12 X 2 24 12 X 1 = = = = 192 144 48 4 72 48 4 12 X 1 + kali 8 Kali 5 Ttk H (6; 2) Kali 3 kali 2 Ttk I (4; 4)

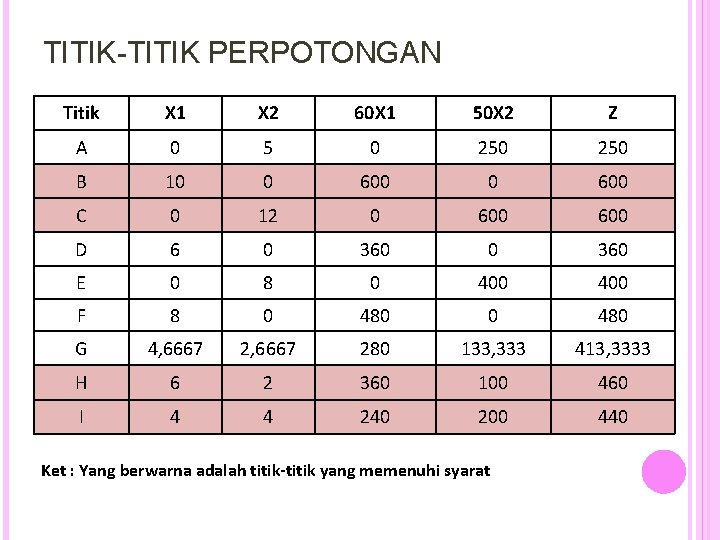
TITIK-TITIK PERPOTONGAN Titik X 1 X 2 60 X 1 50 X 2 Z A 0 5 0 250 B 10 0 600 C 0 12 0 600 D 6 0 360 E 0 8 0 400 F 8 0 480 G 4, 6667 280 133, 333 413, 3333 H 6 2 360 100 460 I 4 4 240 200 440 Ket : Yang berwarna adalah titik-titik yang memenuhi syarat

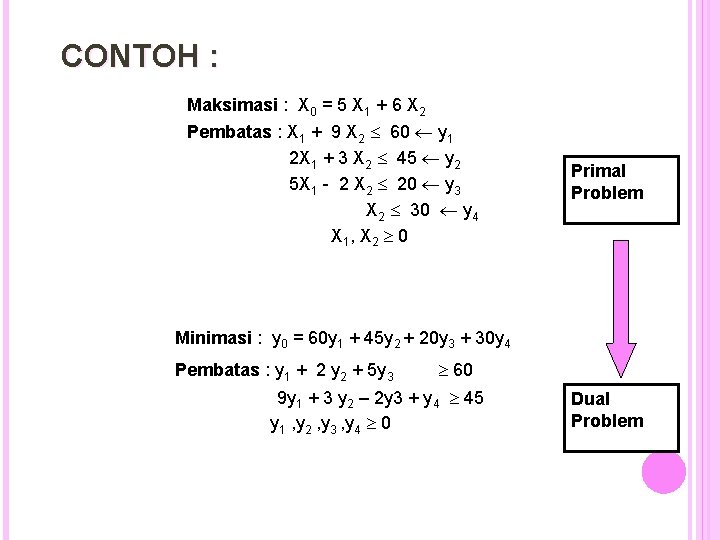
CONTOH : Maksimasi : X 0 = 5 X 1 + 6 X 2 Pembatas : X 1 + 9 X 2 60 y 1 2 X 1 + 3 X 2 45 y 2 5 X 1 - 2 X 2 20 y 3 X 2 30 y 4 X 1, X 2 0 Primal Problem Minimasi : y 0 = 60 y 1 + 45 y 2 + 20 y 3 + 30 y 4 Pembatas : y 1 + 2 y 2 + 5 y 3 60 9 y 1 + 3 y 2 – 2 y 3 + y 4 45 y 1 , y 2 , y 3 , y 4 0 Dual Problem

PENYELESAIAN DUAL SIMPLEX Maksimasi : X 0 = 2 X 1 + X 2 Pembatas : 3 X 1 + X 2 3 4 X 1 + 3 X 2 6 X 1 +2 X 2 3 X 1, X 2 0 Minimasi : X 0 = 2 X 1 + X 2 Pembatas : -3 X 1 - X 2 3 - 4 X 1 - 3 X 2 6 X 1 +2 X 2 3 X 1, X 2 0 Dengan mengubah fungsi obyektif Maksimasi menjadi Minimasi dan fungsi pembatasnya menjadi bertanda , kemudian dibentuk tabel simpleksnya adalah sbb :

PENYELESAIAN DUAL SIMPLEX Metoda Simpleks yang biasa, memberikan hasil didasarkan pada kondisi optimalitas dan layak (feasibility), sebagai berikut : � Kondisi Layak : ‘Leaving Variabel’ adalah variabel basis yang mempunyai nilai paling negatif. � Kondisi Optimalitas : ‘Entering Variabel’ dipilih diantara non-variabel basis dengan cara Rasio dari koefisien fungsi obyektif dengan koefisien pembatas yang terpilih sebagai ‘leaving var’. ‘Entering Var. adalah satu yang mempunyai rasio terkecil untuk problem minimasi, atau nilai terkecil absolut untuk problem maksimasi.

PENYELESAIAN DUAL SIMPLEX Merubah fungsi pembatas dari Ketidaksamaan kedalam bentuk Persamaan Minimasi : X 0 = 2 X 1 + X 2 Pembatas : -3 X 1 - X 2 + S 1 =-3 - 4 X 1 - 3 X 2 + S 2 =-6 X 1 +2 X 2 + S 3 = 3 X 1, X 2 0

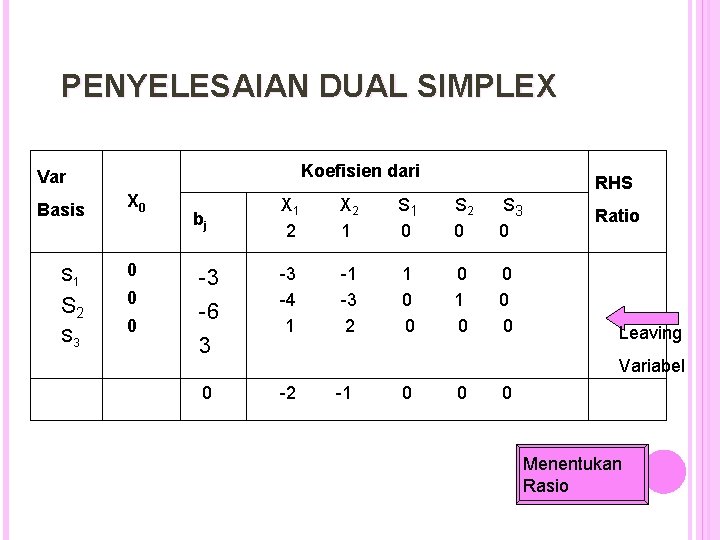
PENYELESAIAN DUAL SIMPLEX Koefisien dari Var Basis S 1 S 2 S 3 X 0 0 bj -3 -6 3 0 RHS X 1 2 X 2 1 S 1 0 S 2 0 S 3 0 -3 -4 1 -1 -3 2 1 0 0 0 0 Ratio Leaving Variabel -2 -1 0 0 0 Menentukan Rasio

UNTUK MENDAPATKAN ENTERING VARIABEL DENGAN MEMILIH NILAI RASIO Variabel X 1 X 2 S 1 S 2 S 3 X 0 – equation -2 -1 0 0 0 S 2 – equation -4 -3 0 1 0 (leaving var) Rasio 1/2 1/3 X 2 terpilih sebagai entering variabel karena merupakan nilai terkecil (minimasi problem) Kembali

PENYELESAIAN DUAL SIMPLEX Koefisien dari Var Basis S 1 X 0 0 X 2 1 S 3 0 bj -1 2 RHS X 1 2 X 2 1 S 1 0 S 2 0 S 3 0 -5/3 4/3 -5/3 0 1 0 0 -1/3 2/3 0 0 1 -2/3 0 0 -1/3 0 Ratio Leaving Variabel Hasil optimal tapi belum feasibel maka dengan cara yang sama seperti iterasi sebelumnya dilakukan perhitungan untuk mendapatkan hasil yang optimal dan feasibel.

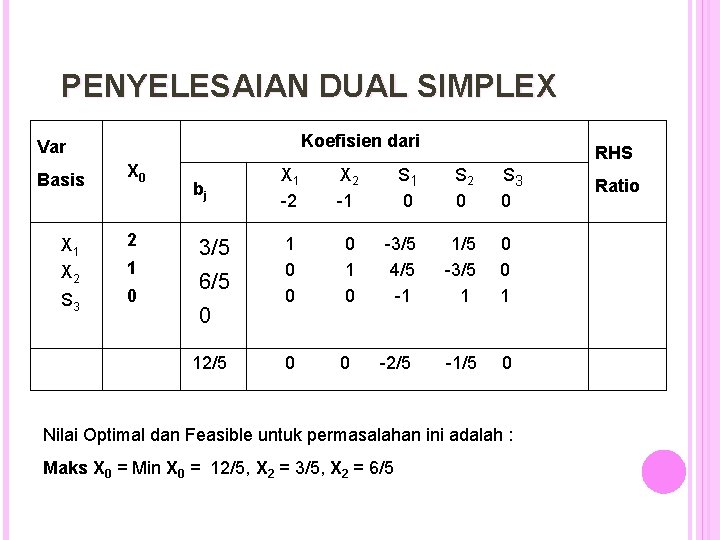
PENYELESAIAN DUAL SIMPLEX Koefisien dari Var Basis X 1 X 0 2 X 2 1 S 3 0 bj 3/5 6/5 0 12/5 RHS X 1 -2 X 2 -1 S 1 0 S 2 0 S 3 0 1 0 0 0 1 0 -3/5 4/5 -1 1/5 -3/5 1 0 0 -2/5 -1/5 0 Nilai Optimal dan Feasible untuk permasalahan ini adalah : Maks X 0 = Min X 0 = 12/5, X 2 = 3/5, X 2 = 6/5 Ratio

CONTOH SOAL : Perusahaan sepatu ‘IDEAL’ membuat 2 macam sepatu. Yang pertama adalah sepatu dengan sol karet (X 1), dan yang kedua adalah sepatu dengan sol dari kulit (x 2). Untuk memproduksi kedua macam sepatu tersebut perusahaan menggunakan 3 jenis mesin. Mesin 1 = Khusus untuk membuat sepatu dari karet, dng kapasitas max. = 8 jam. Mesin 2 = Khusus untuk membuat sepatu dari kulit, dng kapasitas max. = 15 jam. Mesin 3 = Khusus untuk asemblim kedua macam sepatu tsb. , dng kapasitas max. =30 jam Setiap lusin X 1 mula-mula dikerjakan di mesin 1 selam 2 jam, dan selanjutnya menuju mesin 3 selama 6 jam. Sedangkan x 2 dikerjakan oleh mesin 2 selama 3 jam dan langsung ke mesin 3 selama 5 jam. Sumbangan terhadap laba untuk setiap sepatu X 1 = Rp 30. 000, -, sedangkan sepatu x 2 = Rp 50. 000, - Untuk mendapatkan hasil yang optimal, berapakah Sepatu X 1 dan x 2 yang harus diproduksi ?

TABEL PRIMAL-DUAL UNTUK CONTOH DI ATAS Penyajian dalam persamaan Primal – Dual Maksimumkan : Z = 3 X 1+ 5 X 2 Minimumkan : Yo = 8 Y 1+ 15 Y 2 + 30 Y 3 Batasan-batasan : 2 X 1 8 3 X 2 15 6 X 1+ 5 X 2 30 2 Y 1 + 6 Y 3 3 3 Y 2 + 5 Y 3 5 dan X 1, X 2 0 Y 1, Y 2, Y 3 0

TABEL OPTIMAL SIMPLEX-NYA : Solusi Optimalnya - Simplexnya : X 1 = 5/6 X 2 =5 Laba = 27 ½ Dengan cara sama, solusi optimal masalah Dual-nya adalah : Y 1 =0 Y 2 = 5/6 Y 3 =½

Penjelasan : Perhatikan ! Ketiga nilai tersebut sama dengan koefisien slack variabel pada baris pertama (Z) Nilai ini juga menunjukkan kontribusi per satuan sumber I (produk) terhadap laba Contoh : untuk Y 3 = ½ kendala 3 Bila kapasitas mesin 3 ( batasan ke-3) dapat dinaikkan dari 6 X 1 + 5 X 2 30 menjadi 6 X 1 + 5 X 2 31, maka X 1, X 2, dan laba akan berubah menjadi : 6 X 1 + 5 X 2 = 31 x 3 3 X 2 = 15 x 5 ------------------18 X 1 + 15 X 2 = 93 15 X 2 = 75 ------------------18 X 1 = 18 X 1 X 2 =1 =5 Sehingga nilai Z-nya adalah : Z* = 3(1) + 5(5) = 28, naik ½ dibanding sebelumnya.

Tetapi kenaikan ada batasnya ( dalam contoh, max. 19 ), Bagaimana kalau naik 50 ? 6 X 1+ 5 X 2 = 50 x 3 3 X 2 = 15 x 5 -------------18 X 1 + 15 X 2 = 93 15 X 2 ------------------18 X 1 = 75 X 1 = 4 1/6 ini sudah melanggar batasan ke-1, dimana : 2 X 1 8, sehingga X 1 4 Begitu pula dengan kenaikan-kenaikan kapasitas pada batasan lainnya.

ANALISIS SENSITIVITAS Manfaat utama : menghindari perhitungan ulang yang dapat terjadi bila ternyata terjadi perubahan-perubahan pada masalah awal, seperti perubahan : Perubahan pada nilai kanan fungsi batasan � Perubahan pada koefisien fungsi tujuan � Penambahan variabel baru � Penambahan batasan baru � Perubahan pada koefisien yang menunjukkan berapa bagian kapasitas sumber yang di-‘konsumsi’ oleh satuan kegiatan � Perubahan-perubahan tsb. Akan mengakibatkan salah satu dibawah ini : � Penyelesaian optimal tidak berubah � Variabel-variabel dasar mengalami perubahan, tapi nilainya tidak berubah �

TUGAS : SOAL Minimum Z Pembatas 103 • = 40 X 1 + 3 X 1 + 45 X 2 ≥ 12 X 1 + 5 X 2 ≥ Selesaikan soalnya dan gambar grafiknya 114