MANAJEMEN KUANTITATIF MODEL PENUGASAN ASSIGNMENT Pertemuan ke 7

MANAJEMEN KUANTITATIF MODEL PENUGASAN (ASSIGNMENT) Pertemuan ke 7

MODEL PENUGASAN Ø Model Penugasan berhubungan dengan persoalan bagaimana mengalokasikan (mendistribusikan) beberapa tugas ke beberapa pelaksana. Ø Masalah yang berhubungan dengan penugasan optimal dari bermacam-macam sumber yang produktif atau personalia yang mempunyai tingkat efisiensi yang berbeda-beda untuk tugas-tugas yang berbeda-beda pula

TUJUAN MODEL PENUGASAN �Bagaimana menentukan alokasi yang optimal untuk dapat meminimumkan biaya atau mengoptimalkan/memaksimumkan laba/keuntungan

KARAKTERISTIK MODEL PENUGASAN Objek dalam masalah penugasan mempunyai jumlah tertentu 2. Setiap tugas hanya boleh dilakukan oleh satu pelaksana atau sebaliknya 3. Hasil dari setiap penugasan dalam bentuk matrik biaya atau keuntungan 1.

LANGKAH PENYELESAIAN MODEL PENUGASAN DENGAN METODE HUNGARIAN 1. Reduksi baris (pelaksana) Nilai pada setiap baris dikurangi dengan nilai terkecil pada baris tersebut, hasilnya dimasukkan ke dalam tabel baru. 2. Reduksi kolom (tugas) Nilai pada setiap kolom pada tabel yang baru dikurangi dengan nilai terkecil pada kolom tersebut, kemudian dibuat tabel baru 3. Memeriksa tugas dengan menggunakan aturan garis lurus minimum yang melalui nilai nol Buat garis yang melalui angka nol yang ada dalam tabel. Jika jumlah baris garis yang minimum = jumlah baris/kolom, maka penugasan sudah optimal dan dilanjutkan ke langkah 6. Jika penugasan belum optimal, maka akan dilanjutkan ke langkah 4. Modifikasi tabel a. Nilai dalam tabel yang tidak dilalui oleh garis dikurangi dengan nilai terkecil yang tidak dilalui oleh garis. b. Nilai terkecil yang tidak dilalui oleh garis ditambahkan pada nilai yang merupakan perpotongan garis 5. 6. Kembali ke langkah (3) Membuat penugasan optimal Setiap pasangan tunggal baris (pelaksana) dan kolom (tugas) harus memiliki nilai 0

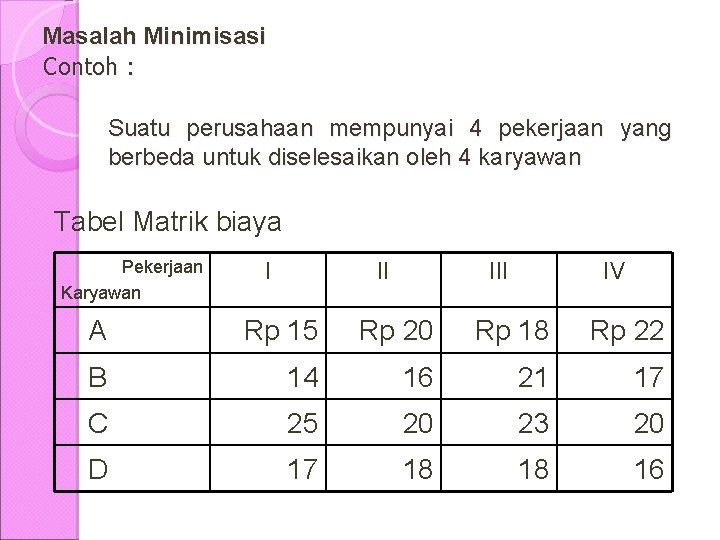
Masalah Minimisasi Contoh : Suatu perusahaan mempunyai 4 pekerjaan yang berbeda untuk diselesaikan oleh 4 karyawan Tabel Matrik biaya Pekerjaan Karyawan I II IV A Rp 15 Rp 20 Rp 18 Rp 22 B 14 16 21 17 C 25 20 23 20 D 17 18 18 16

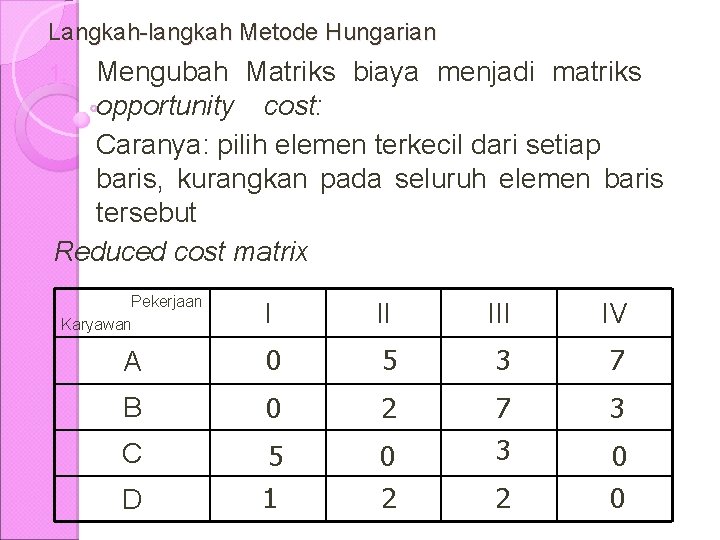
Langkah-langkah Metode Hungarian Mengubah Matriks biaya menjadi matriks opportunity cost: Caranya: pilih elemen terkecil dari setiap baris, kurangkan pada seluruh elemen baris tersebut Reduced cost matrix 1. Pekerjaan Karyawan I II IV A Rp 0 15 Rp 5 20 3 18 Rp 7 22 Rp B 0 14 2 16 3 17 C 5 25 1 17 0 20 2 18 7 21 3 23 D 2 18 0 20 0 16

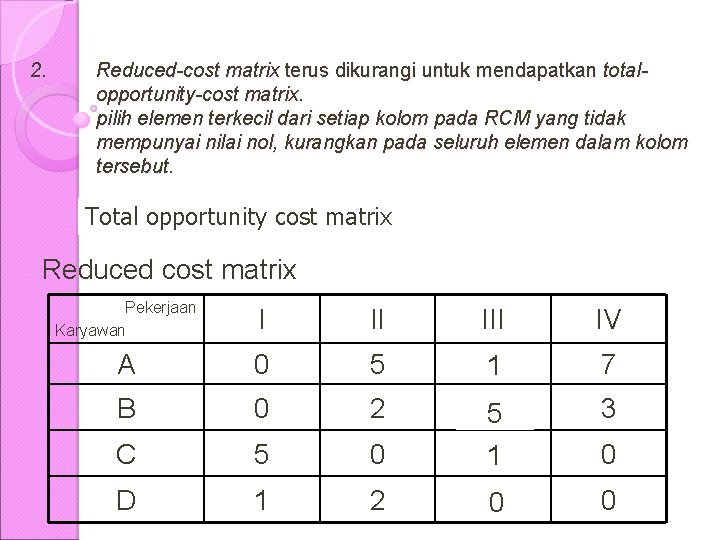
2. Reduced-cost matrix terus dikurangi untuk mendapatkan totalopportunity-cost matrix. pilih elemen terkecil dari setiap kolom pada RCM yang tidak mempunyai nilai nol, kurangkan pada seluruh elemen dalam kolom tersebut. Total opportunity cost matrix Reduced cost matrix Pekerjaan Karyawan I II IV A 0 5 31 7 B 0 2 3 C 5 0 75 31 D 1 2 20 0 0

3. Melakukan test optimalisasi dengan menarik sejumlah minimum garis horisontal dan/atau vertikal untuk meliput seluruh elemen bernilai nol Penugasan optimal adalah feasible jika : jumlah garis = jumlah baris atau kolom Test of optimality Pekerjaan I Karyawan II IV A 0 5 1 7 B 0 2 5 3 C 5 0 1 0 D 1 2 0 0

4. Untuk merevisi total-opportunity matrix, pilih elemen terkecil yang belum terliput garis (1) untuk mengurangi seluruh elemen yang belum terliput Tambahkan jumlah yang sama pada seluruh elemen yang mempunyai dua garis yang saling bersilangan Ulangi langkah 3 Revised matrix dan Test of optimality Pekerjaan I II III Karyawan A 0 B C 0 6 5 D 2 1 IV 45 12 10 4 5 7 6 2 3 0 1 0 2 0 0

Melakukan test optimalisasi dengan menarik sejumlah minimum garis horisontal dan/atau vertikal untuk meliput seluruh elemen bernilai nol Karena jumlah garis = jumlah baris atau kolom maka matrik penugasan optimal telah tercapai Revised matrix dan Test of optimality Pekerjaan Karyawan I II IV A 0 B 10 4 5 7 6 2 3 C 0 6 5 45 12 0 1 0 D 2 1 2 0 0

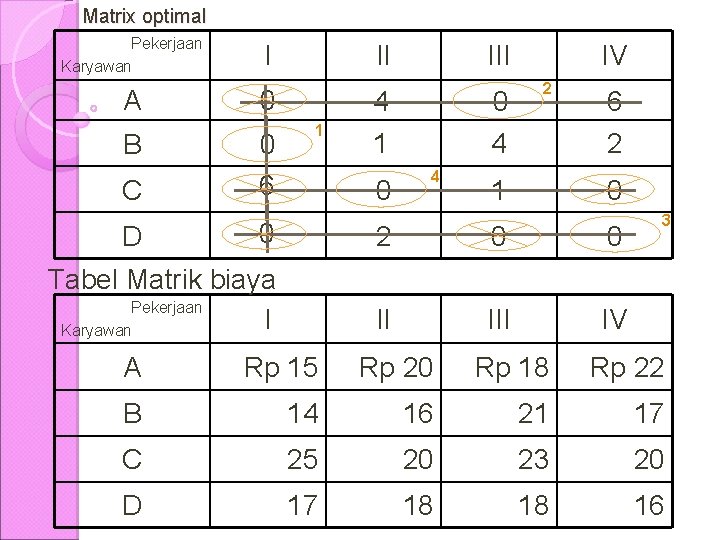
Matrix optimal Pekerjaan Karyawan A B C I II 0 0 6 5 1 III 45 12 0 10 4 5 4 IV 2 1 7 6 2 3 0 0 1 2 0 0 Tabel Matrik biaya Pekerjaan I Karyawan II IV D 3 A Rp 15 Rp 20 Rp 18 Rp 22 B 14 16 21 17 C 25 20 23 20 D 17 18 18 16

Skedul penugasan optimal Skedul penugasan A - III Rp 18 B -I 14 C - II 20 D - IV 16 Rp 68 Karyawan B ditugaskan untuk pekerjaan satu karena baris B hanya mempunyai satu nilai nol

Masalah Maksimisasi Contoh : Suatu perusahaan mempunyai 5 pekerjaan yang berbeda untuk diselesaikan oleh 5 karyawan Tabel Matrik keuntungan Pekerjaan Karyawan I II IV V A Rp 10 Rp 12 Rp 10 Rp 8 Rp 15 B 14 10 9 15 13 C 9 8 7 8 12 D 13 15 8 16 11 E 10 13 14 11 17

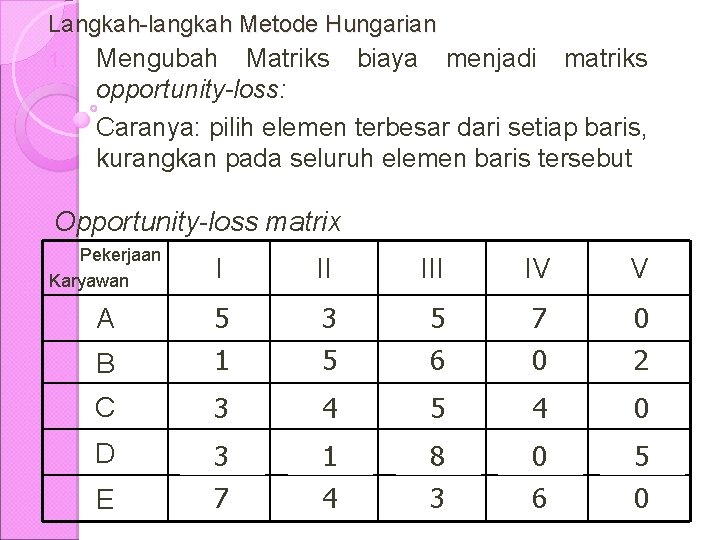
Langkah-langkah Metode Hungarian 1. Mengubah Matriks biaya menjadi matriks opportunity-loss: Caranya: pilih elemen terbesar dari setiap baris, kurangkan pada seluruh elemen baris tersebut Opportunity-loss matrix Pekerjaan Karyawan I II IV V B Rp 5 10 1 14 Rp 3 12 5 10 C 3 9 4 8 5 7 4 8 0 12 D 3 13 7 10 1 15 4 13 8 8 3 14 0 16 6 11 5 11 0 17 A E Rp 5 10 Rp 7 8 Rp 0 15 6 9 0 15 2 13

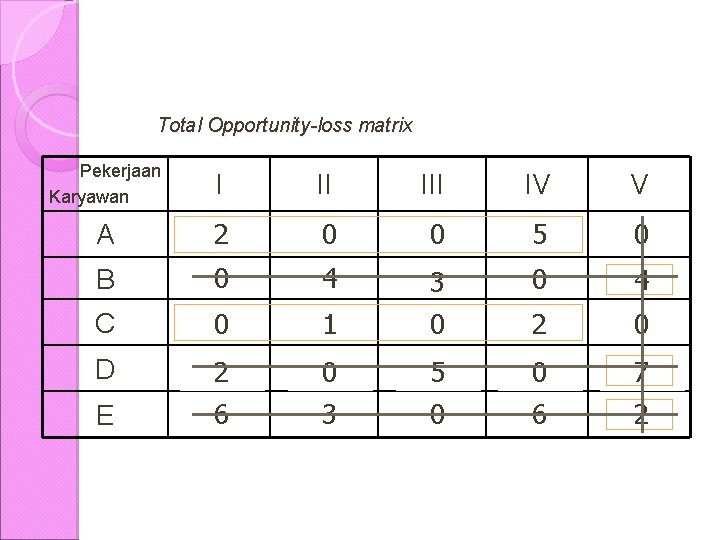
Total Opportunity-loss matrix Pekerjaan Karyawan I II A 2 5 10 Rp 4 3 0 12 Rp 2 B 0 1 14 4 5 10 C 2 0 3 9 D 3 13 2 6 7 10 E III IV V 5 0 10 Rp 7 5 8 Rp 0 15 Rp 2 0 15 2 4 13 4 3 1 8 6 9 3 5 2 0 7 4 2 8 0 12 1 15 0 4 13 3 8 8 5 3 14 0 0 16 5 7 11 0 2 17 6 11

Karena jumlah garis = jumlah baris atau kolom maka matrik penugasan optimal telah tercapai Total Opportunity-loss matrix Pekerjaan Karyawan A B C D E I II 5 4 10 Rp 2 4 0 14 1 0 3 2 9 3 2 13 6 10 7 III 2 3 0 12 Rp 2 4 5 10 4 3 1 8 0 15 1 3 4 13 IV V 5 0 10 Rp 7 5 8 Rp 0 15 Rp 2 6 9 3 5 2 0 7 5 8 8 1 0 3 14 0 15 4 2 8 3 0 16 6 11 2 4 13 5 0 12 5 7 11 2 17 0

SEKIAN