Managing Portfolios Theory Chapter 3 Modern Portfolio Theory

Managing Portfolios: Theory Chapter 3 Modern Portfolio Theory Capital Asset Pricing Model Arbitrage Pricing Theory Lecture #3 All Rights Reserved 1

Learning Objectives n Basics of Investment Theories n Review Efficient Markets Hypothesis (EMH) n Modern Portfolio Theory (MPT) n Application and Implications n Capital Asset Pricing Theory (CAPM) n Application and Implications n Arbitrage Pricing Theory n The “UFO” of Investment Theory Lecture #3 All Rights Reserved 2

Basics of Investment Theories n Investment Returns are a function of Risk n Risk is a function of Uncertainty n The degree of uncertainty may be defined by a probability distribution n The shape of [future] probability distributions are much more art than science n Bottom line: don’t be fooled or led astray by the mathematical elegance of theories to be discussed. Lecture #3 All Rights Reserved 3

Efficient Markets Theory n Efficient Markets Hypothesis (EMH) n Implication: you cannot consistently beat the market n Prices Reflect all information n Past (Weak form efficiency) n Present or New (Semi-Strong form efficiency) n Inside (Strong form efficiency) n Results of Academic Research n Markets mostly weak form efficient n Several Anomalies question semi-strong efficiency n Insiders consistently outperform the market n Best you can do is manage risk n More on EMT/EMH in Chapter 5 Lecture #3 All Rights Reserved 4

Modern Portfolio Theory (Markowitz) n MPT: 2 Sources of Risk n Variation n Covariance n Risk Management Strategy n Hold a diversified portfolio of assets n The more assets, the lower the risk n Assets are considered in terms of the variance and covariance they add to the portfolio Lecture #3 All Rights Reserved 5

Modern Portfolio Theory (Markowitz) n Riskiness of a Two-Asset Portfolio n P 2 = w 12 12 + w 22 22 + 2 w 1 w 2 cov 1, 2 n Subject to: w 1 + w 2 = 1 n Covariance (Correlation [r]) n 2 assets may covary n n n Positively (move in same direction) r > 0 Not at all (zero – no correlation) r = 0 Negatively (move in opposite directions) r < 0 Least risk 2 -asset portfolio? When cov 1, 2 < 0 n Most risky 2 -asset portfolio? When cov 1, 2 > 0 n Lecture #3 All Rights Reserved 6

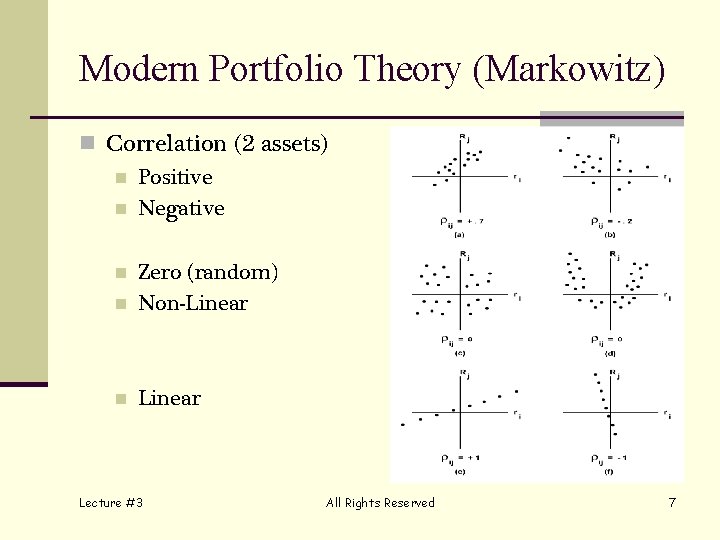
Modern Portfolio Theory (Markowitz) n Correlation (2 assets) n Positive n Negative n Zero (random) Non-Linear n Lecture #3 All Rights Reserved 7

Modern Portfolio Theory (Markowitz) n Return on a Two-Asset Portfolio n E (Rp) = w 1 E(R 1) + w 2 E(R 2) n General Form of MPT E(RP) = S wi E (Ri) n P 2 = S wi 2 + S S wi wj covi, j n Subject to: S wi = 1 n Lecture #3 All Rights Reserved 8

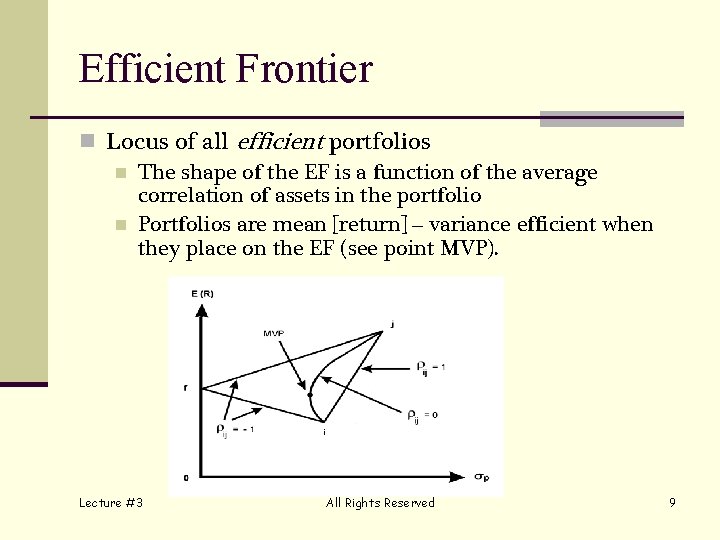
Efficient Frontier n Locus of all efficient portfolios n The shape of the EF is a function of the average correlation of assets in the portfolio n Portfolios are mean [return] – variance efficient when they place on the EF (see point MVP). Lecture #3 All Rights Reserved 9

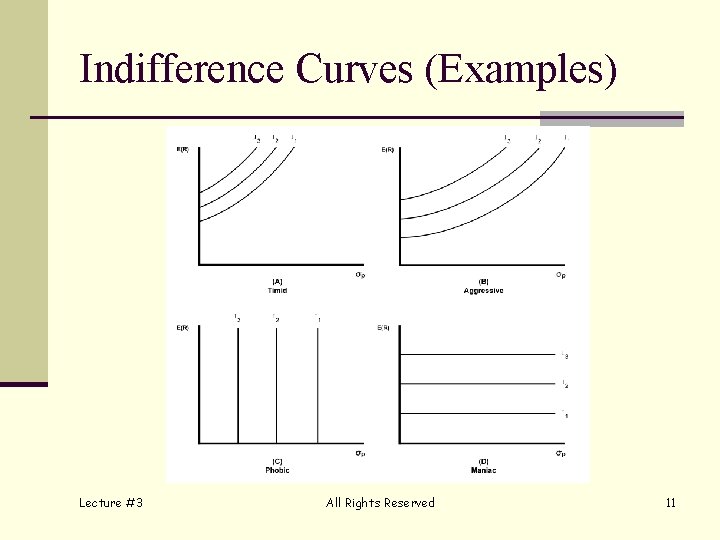
Selecting a Portfolio n Risk Preferences or Indifference n Investors are generally assumed to be risk averse. n n n Prefer less risk to more for a given rate of return Prefer a higher return for a given level of risk Indifference curves tell us something about our utility functions relative to wealth. n n n Lecture #3 How much do we value an additional unit of wealth? How much are we willing to risk to obtain it? See Figure 3 -8 on page 3. 20 All Rights Reserved 10

Indifference Curves (Examples) Lecture #3 All Rights Reserved 11

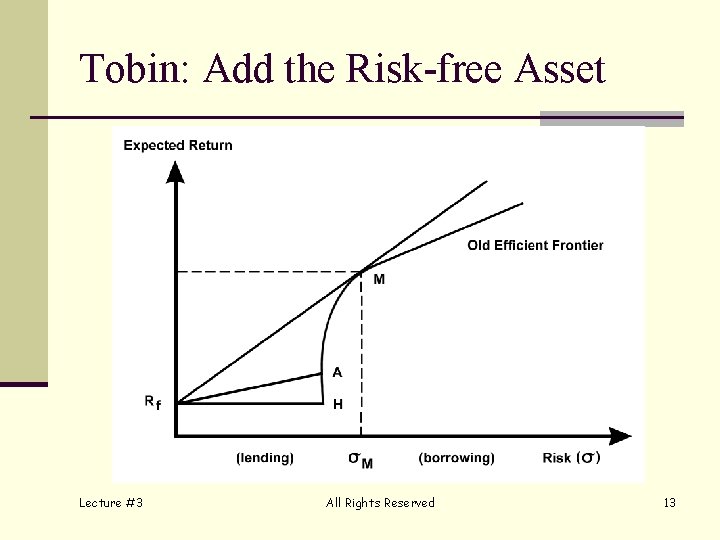
Tobin MPT Extension n Major drawbacks to MPT n Computing Variance-Covariance Matrix n Mathematics for Selecting Assets n James Tobin (1958): suppose we consider a risk-free (RF) asset combined with the EF A straight line EF results n 2 -Asset PF: RF and M (risky [market] portfolio) n See Figure 3 -14 on page 3. 31 n Lend and Borrow at the RF rate n Lecture #3 All Rights Reserved 12

Tobin: Add the Risk-free Asset Lecture #3 All Rights Reserved 13

Market Portfolio as Construct n Hypothetical portfolio representing each investment asset in the world in proportion to its relative weight in the universe of investment assets n Index Construction Value weighted n Equal weighted n Lecture #3 All Rights Reserved 14

Separation Theorem n Return to any efficient portfolio and its risk can be completely described by appropriate weighted average of two assets the risk-free asset n the market portfolio n n Two separate decisions n What risky investments to include in the market portfolio n How one should divide one’s money between the market portfolio and risk-free asset Lecture #3 All Rights Reserved 15

Capital Asset Pricing Theory (Sharpe) n The concept of Beta (b) n Assuming the existence of a mean and variance efficient market portfolio, how can we construct an portfolio of risky assets with a known risk attribute? n More or less risky than M Beta = a measure of asset risk relative to the market portfolio (M). n b = covi, M / M 2 n b = (ri, M i) / M n Lecture #3 All Rights Reserved 16

Capital Asset Pricing Theory (Sharpe) n Implications of Beta Value n Beta < 0: moves opposite to the market n Beta = 0: independent of the market n 0 < Beta < 1: less risky than market n Beta = 1: risk identical to the market n Beta > 1 => more risky than market Lecture #3 All Rights Reserved 17

Capital Asset Pricing Theory (Sharpe) n Estimating Beta (CAPM) n b is a simple OLS regression coefficient n General Form: y = a + bx + e n OLS: Ri = a + b RM n CAPM: E (Ri) = E (RF) + b {E (RM) – E (RF)} n {E (RM) – E (RF)} is defined as the risk premium n B is defined as the amount of risk n b {E (RM) – E (RF)} is the price of risk n ri = rf + (rm – rf) bi n Portfolio Beta = S Wi bi Lecture #3 All Rights Reserved 18

Capital Asset Pricing Theory (Sharpe) n The Capital Market Line (CML) n Graphing CAPM for market portfolio n The Security Market ri = rf + (rm – rf) bi Line (SML) n Graphing CAPM for security i Lecture #3 All Rights Reserved 19

Capital Asset Pricing Theory (Sharpe) n Market Risk vs. Nonmarket Risk i 2 = (beta 2 x M 2 ) + eta 2 Total risk = market risk + nonmarket risk Lecture #3 All Rights Reserved 20

CAPM Issues n What return frequency should we use? n Daily, weekly, monthly, quarterly n What constitutes the market portfolio? n SP 500 as a proxy n Other proxies yield different b estimates n Central tendency characteristic of Beta n Coefficient of Determination (R 2) varies widely for individual securities. Lecture #3 All Rights Reserved 21

Arbitrage Pricing Theory (APT) n Generalized Multi-Factor Pricing Model n Factors are the Eigen values derived from a variance covariance matrix. n Factors are said to “load” on economic/market constructs. n Biggest problem is the nature and reliability of loading. Lecture #3 All Rights Reserved 22

Woerheide's Final Thoughts on Portfolio (Investment) Theories n Uniform Principal and Income Act (1931) n Prudent man rule has evolved to prudent investor n A [poor? ] model is better than no model n Departure point for how we think about what is happening in security markets Lecture #3 All Rights Reserved 23