Managing Flow Variability Process Control Performance Variability All

Managing Flow Variability Process Control

Performance Variability All internal and external performance measures display vary from tome to time. n n External Measurements - customer satisfaction, product rankings, customer complaints. Internal Measurements - flow units cost, quality, and time. No two cars rolling off an assembly line have identical cost. No two customers for identical transaction spend the same time in a bank. The same meal you have had in two different occasions in a restaurant do not taste exactly the same. p Sources of Variability n n Internal: imprecise equipment, untrained workers, and lack of standard operating procedures. External: inconsistent raw materials, supplier delays, consumer taste change, and changing economic conditions. Process Control, A. Asef-Vaziri, Systems & Operations Management. 2

Performance Variability p A discrepancy between the actual and the expected performance often leads to cost↑, flow time↑, quality↓ dissatisfied customers. p Processes with greater variability are judged less satisfactory than those with consistent, predictable performance. p What is the base of the customer judgment the exact unit of product or service s/he gets, not how the average product performs. Customers perceive any variation in their product or service from what they expected as a loss in value. p In general, a product is classified as defective if its cost, quality, availability or flow time differ significantly from their expected values, leading to dissatisfied customers. Process Control, A. Asef-Vaziri, Systems & Operations Management. 3

Quality Management Terms p Quality of Design. How well product specifications aim to meet customer requirements (what we promise consumers ~ in terms of what the product can do). Quality Function Deployment (QFD) is a conceptual framework for translating customers’ functional requirements (such as ease of operation of a door or its durability) into concrete design specifications (such as the door weight should be between 75 and 85 kg. ) p Quality of Conformance. How closely the actual product conforms to the chosen design specifications. Ex. # defects per car, fraction of output that meets specifications. Ex. irline conformance can be measured in terms of the percentage of flights delayed for more than 15 minutes OR the number of reservation errors made in a specific period of time. Process Control, A. Asef-Vaziri, Systems & Operations Management. 4

Cost of Quality Assurance: Appraisal & Prevention Costs p Appraisal Costs. Measuring and monitoring activities related to quality. Checking of incoming material, process setup, and products and compare with expectations. Reviewing and ensuring that the quality system is functioning correctly. Assessment and approval of suppliers of products and services. p Prevention Costs. Prevention costs are incurred to prevent or avoid quality problems. These costs are associated with the design, implementation, and maintenance of the quality management system. They are planned and incurred before actual operation. They could include establishment of specifications, quality planning, and quality assurance for incoming materials, processes, finished products, and services, training workers to perform their jobs according to methods and standards, improving methods, standards, and technology. Process Control, A. Asef-Vaziri, Systems & Operations Management. 5

Cost of Quality Non-Conformance: Internal & External Failure Costs Internal failure costs. Costs to remedy defects discovered before the product or service is delivered to the customer. They include waste of recourses as a result of errors, poor organization, or communication, defective product or material that cannot be repaired, used, or sold, rework to correct defective material or errors. Failure analysis tries to establish the causes of internal product or service failure External failure costs. Costs to remedy defects not detected until after transfer to the customer. They include replace repairs and servicing of failed products. Process Control, A. Asef-Vaziri, Systems & Operations Management. 6

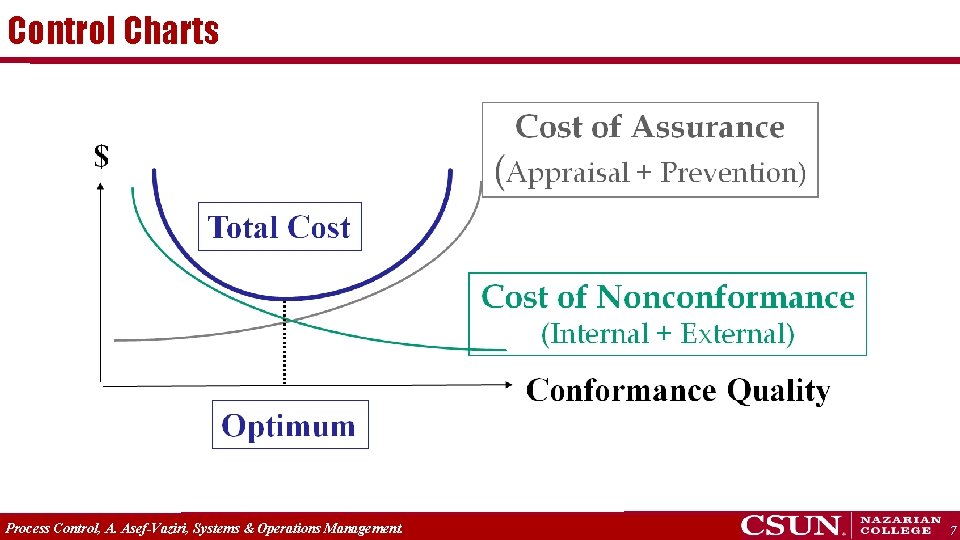
Control Charts Process Control, A. Asef-Vaziri, Systems & Operations Management. 7

The Garage Door Manufacturer According to the sales manager of a high-tech manufacturer of garage doors, while the company has 15% of market share, customers are not satisfied n n Door Quality in terms of safety, durability, and ease of use High Price compared competitors’ process Not on-time orders Poor After Sales Service We can not rely of subjective statements and opinions n n Collect and analyze concrete data –facts- on performance measures that drive customer satisfaction Identify, correct, and prevent sources of future problems Process Control, A. Asef-Vaziri, Systems & Operations Management. 8

Tools for Analysis of Process Variability p Check Sheet. A Table showing the types and frequency of problems. p Pareto Chart. A bar chart of of Check Sheet in non-increasing order. p The 80 -20 Pareto Principle. 20% of problem types account for 80% of all occurrences. p Histogram. A bar plot that displays the frequency distribution. Ex. 14% of the doors weighed about 83 kg, 8% weighed about 81 kg, and so forth. Pareto Chart Histogram Check Sheet Process Control, A. Asef-Vaziri, Systems & Operations Management. 9

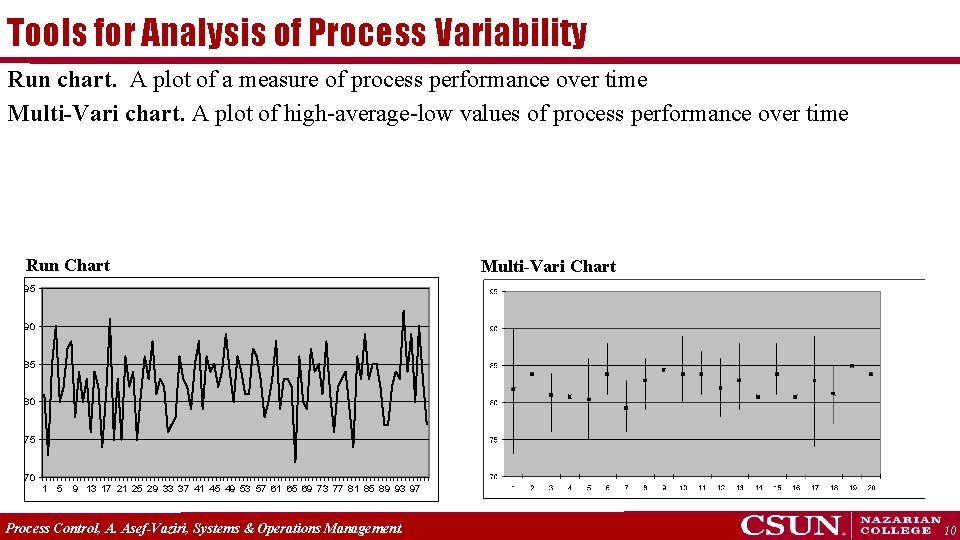
Tools for Analysis of Process Variability Run chart. A plot of a measure of process performance over time Multi-Vari chart. A plot of high-average-low values of process performance over time Run Chart Multi-Vari Chart 95 90 85 80 75 70 1 5 9 13 17 21 25 29 33 37 41 45 49 53 57 61 65 69 73 77 81 85 89 93 97 Process Control, A. Asef-Vaziri, Systems & Operations Management. 10

Comparison Of Process Measure Tools p Pareto Chart. The importance of each item. Quality was the most important item. Quality was then defined as finish, ease of use, and durability. Ease of use and durability which are subjective, must be translated into some thing measurable. We translate them into weight. If weight is high, it cannot operate easily, if weight is low, it will not be durable. A high quality door, based on engineering design must weight 82. 5 lbs. p Histogram. Shows the tendency (mean) and the standard deviation. Ex. For door weight. p Run Chart. Can show trend. p Multi-Vari Chart. Shows average and variability inside the samples and among the samples. Process Control, A. Asef-Vaziri, Systems & Operations Management. 11

Process Control p If observed performance variability is n n Normal - due to random causes - process is in control Abnormal - due to assignable causes - process is out of control p The short run goal is: 1. 2. 3. 4. Estimate normal stochastic variability. Accept it as an inevitable and avoid tampering Detect presence of abnormal variability Identify and eliminate its sources p The long run goal is to reduce normal variability by improving process. Process Control, A. Asef-Vaziri, Systems & Operations Management. 12

Control Limit Policy p How to decide whether observed variability is normal or abnormal? p Control Limit Policy n Control band - A range within which any variation in performance is interpreted as normal due to causes that cannot be identified or eliminated in short run. n Variability outside this range is abnormal. n Lower limit of acceptable mileage, control band for house temperature. p Process control is useful to control any type of process. p Application of control limit policy n Managing inventory, process capacity and flow time. n Cash management - liquidate some assets if cash falls below a certain level. n Stock trading - purchase a stock if and when its price drops to a specific level. p Control limit policy has usage in a wide variety of business in form of critical threshold for taking action Process Control, A. Asef-Vaziri, Systems & Operations Management. 13

Statistical Process Control p Statistical process control involves setting a “range of acceptable variations” in the performance of the process, around its mean. p If the observed values are within this range: n Accept the variations as “normal” n Don’t make any adjustments to the process p If the observed values are outside this range: n The process is out of control n Need to investigate what’s causing the problems – the assignable cause Process Control, A. Asef-Vaziri, Systems & Operations Management. 14

Process Control Charts p Let be the expected value and be the standard deviation of the performance. Set up an Upper Control Limit (UCL) and a Lower Control Limit (LCL). LCL = - z UCL = + z Decide how tightly to monitor and control the process. The smaller the z, the tighter the control Process Control, A. Asef-Vaziri, Systems & Operations Management. 15

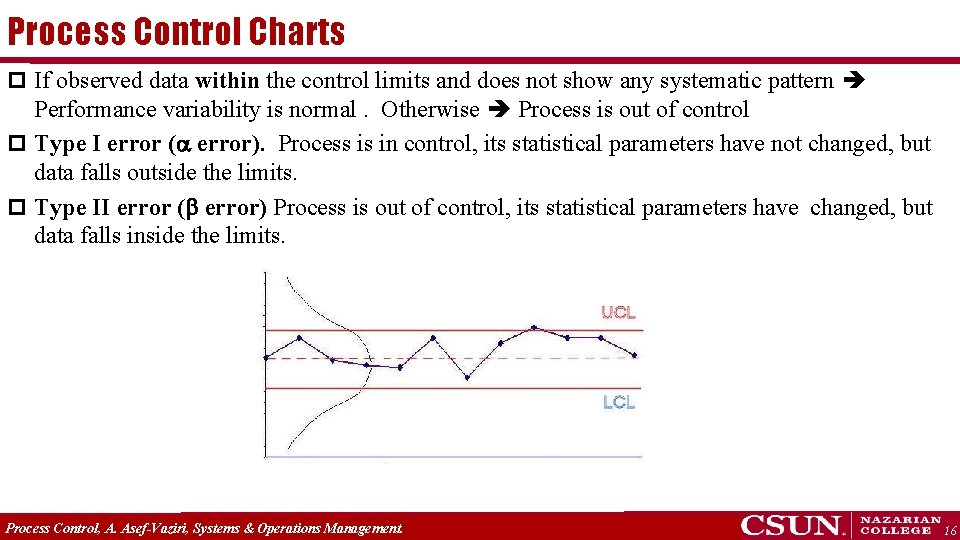
Process Control Charts p If observed data within the control limits and does not show any systematic pattern Performance variability is normal. Otherwise Process is out of control p Type I error ( error). Process is in control, its statistical parameters have not changed, but data falls outside the limits. p Type II error ( error) Process is out of control, its statistical parameters have changed, but data falls inside the limits. Process Control, A. Asef-Vaziri, Systems & Operations Management. 16

Control Charts p Optimal Degree of Control depends on 2 things: n How much variability in the performance measure we consider acceptable n How frequently we monitor the process performance. p Optimal frequency of monitoring is a balance between the costs and benefits p If we set ‘z’ to be too small: We’ll end up doing unnecessary investigation. Incur additional costs. p If we set ‘z’ to be too large: We’ll accept a lot more variations as normal. We wouldn’t look for problems in the process – less costly p In practice, a value of z = 3 is used. 99. 73% of all measurements will fall within the “normal” range p Process Control, A. Asef-Vaziri, Systems & Operations Management. 17

Control Charts Process Control, A. Asef-Vaziri, Systems & Operations Management. 18

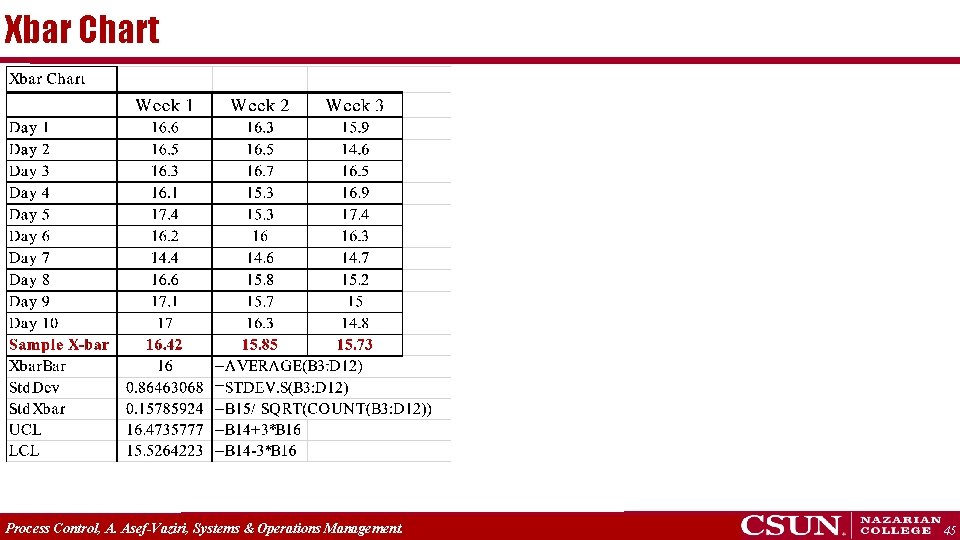
Xbar-Chart We have collected 20 samples, each of size 5, n=5, of our variable of interest X – the door weight in our example. We have 100 pieces of data. We can simple use excel to compute the average and standard deviation of this data. Overall average weight Standard deviation Variance A higher value of the average indicates a shift in the entire distribution to the right, so that all doors produced are consistently heavier. An increase in the value of the standard deviation means a wider spread of the distribution around the mean, implying that many doors are much heavier or lighter than the overall average weight. Process Control, A. Asef-Vaziri, Systems & Operations Management. 19

Xbar-Chart If we compute the average of the random variable X, in each sample of n, in our example 5, and show it by Process Control, A. Asef-Vaziri, Systems &Education Operations Management. Copyright © 2013 Pearson Inc. publishing as 20

Xbar-Chart Therefore, if we compute the average weight door 68. 26% of all doors will weigh within 82. 5 + (1)(1. 88), 95. 44% of doors will weight within 82. 5 + (2)(1. 88), and 99. 73% of door weights will be within 82. 5 + (3)(1. 88), or between and 76. 86 and 88. 14. UCL LCL Process Control, A. Asef-Vaziri, Systems &Education Operations Management. Copyright © 2013 Pearson Inc. publishing as 21

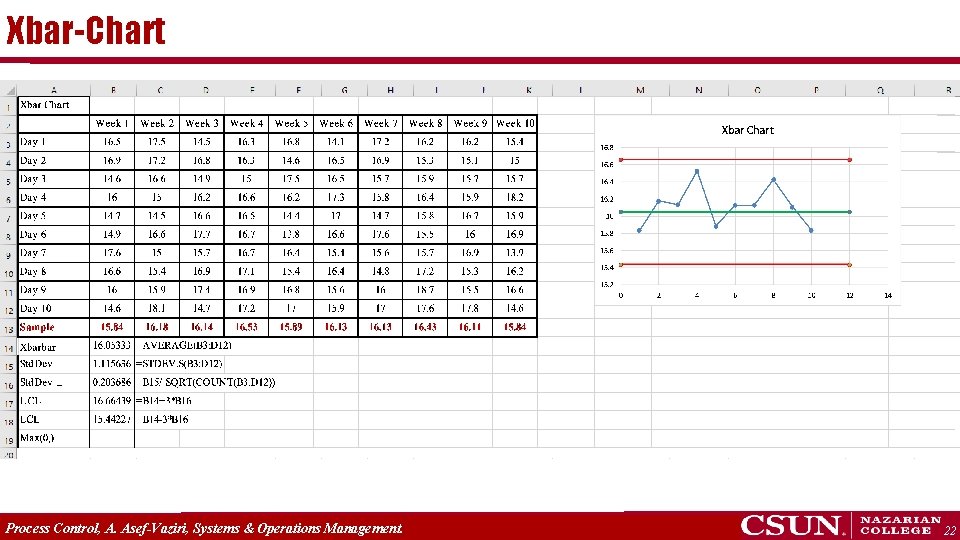
Xbar-Chart Process Control, A. Asef-Vaziri, Systems & Operations Management. 22

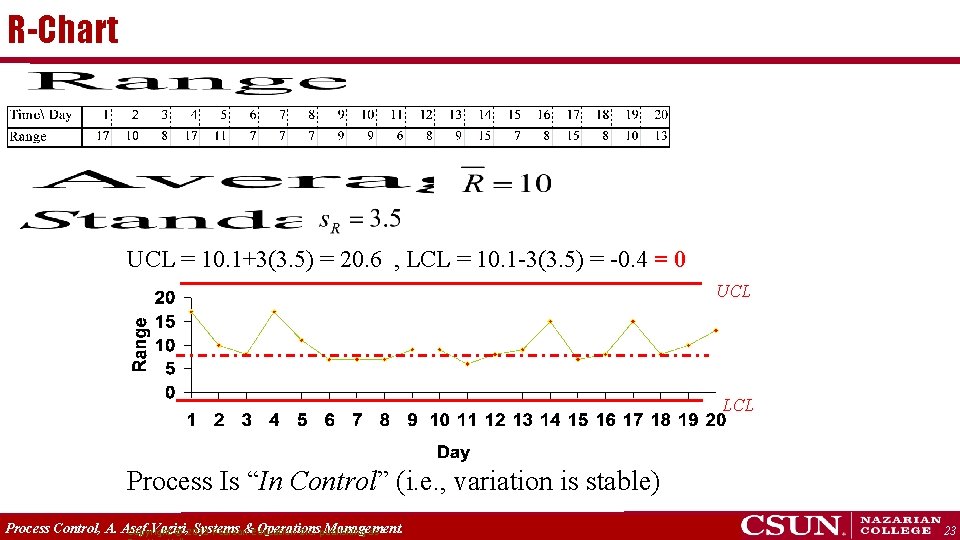
R-Chart UCL = 10. 1+3(3. 5) = 20. 6 , LCL = 10. 1 -3(3. 5) = -0. 4 = 0 UCL LCL Process Is “In Control” (i. e. , variation is stable) Process Control, A. Asef-Vaziri, Systems &Education Operations Management. Copyright © 2013 Pearson Inc. publishing as 23

Fraction Defective - P-Chart p Instead of analysis of Average, Range, etc. we may choose to classify each flow unit as p p defective or nondefective. If we take a single flow unit, probability of being defective is p and not being defective is (1 -p). If we take a random sample of n flow units, then the number of defectives D in the sample will have binomial distribution , which has mean np and variance np(1 – p). The fraction defective of this sample P = D/n will then have mean np/n = p and variance np(1 – p)/n 2. = p(1 – p)/n. To estimate the true fraction defective pbar, we take N samples, each containing n flow units, observe proportion defective in each and compute the average fraction defective. The fraction defective (or p) chart shows control limits on the observed fraction of defective units p Process Control, A. Asef-Vaziri, Systems & Operations Management. 24

P-Chart we classify each garage door as defective or good, depending on its overall quality such as fit and finish, dimensions, weight. Based on 20 samples of 5 doors each, the number of defective doors D in each sample is 1, 0, 0, 2, 1, 1, 0, 1, 2, 1, 0, 3, 0, 1, 0. Dividing each by 5 gives fraction defective in each sample as 0. 2, 0, 0, 0. 4, 0. 2, 0, 0. 2, 0. 4, 0. 2, 0, 0. 6, 0, 0. 2, 0. The average proportion defective is then = 0. 2. With z = 3, If the observed fraction defective is less than 0. 7366, we conclude the process is in control, as is the case above. Process Control, A. Asef-Vaziri, Systems & Operations Management. 25

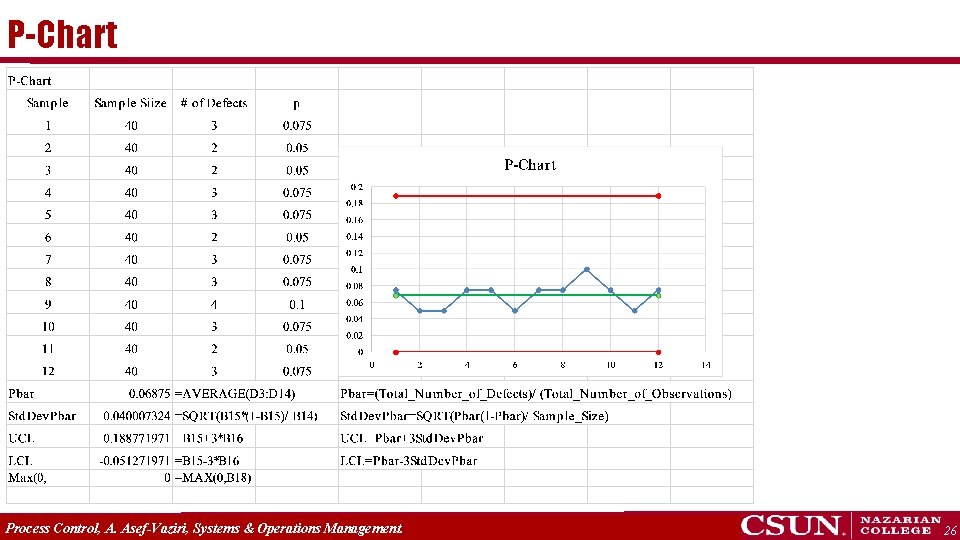
P-Chart Process Control, A. Asef-Vaziri, Systems & Operations Management. 26

Number of Defects – C-Chart n =# of opportunities for defects/errors in a single flow unit p = Probability of a defect/error occurrence in each m = Number of defects/errors per flow unit. Number of typos/page, equipment breakdowns/shift, power outages/year, customer complaints/month, defects/car, accounting errors/thousand transactions, bags lost/thousand flown, . m follows Binomial (n, p) with mean np, variance np(1 -p) If n is large and p is small, then we can assume m follows Poisson distribution with cbar = np. cbar is mean and also variance. If the observed number of errors exceeds the UCL, it indicates degradation in performance. If it is less than the LCL, it indicates better‑than‑expected performance. Process Control, A. Asef-Vaziri, Systems &Education Operations Management. Copyright © 2013 Pearson Inc. publishing as 27

Number of Defects – C-Chart Consider the number of order processing errors that occur per month at Garage Door Operations. If they process several orders per month and the chance of making an error on each order is small, then the number of errors per month follows Poisson distribution. Suppose they have tracked order processing errors over the past 12 months and found them to be 3, 1, 0, 4, 6, 2, 1, 2, 0, 1, 3, and 2. Then the average number of errors per month is 2. 083 Since all observed processing errors are less than 6. 413 (even though we made 6 order processing errors in month 5), we conclude that the order processing process is in control. Process Control, A. Asef-Vaziri, Systems &Education Operations Management. Copyright © 2013 Pearson Inc. publishing as 28

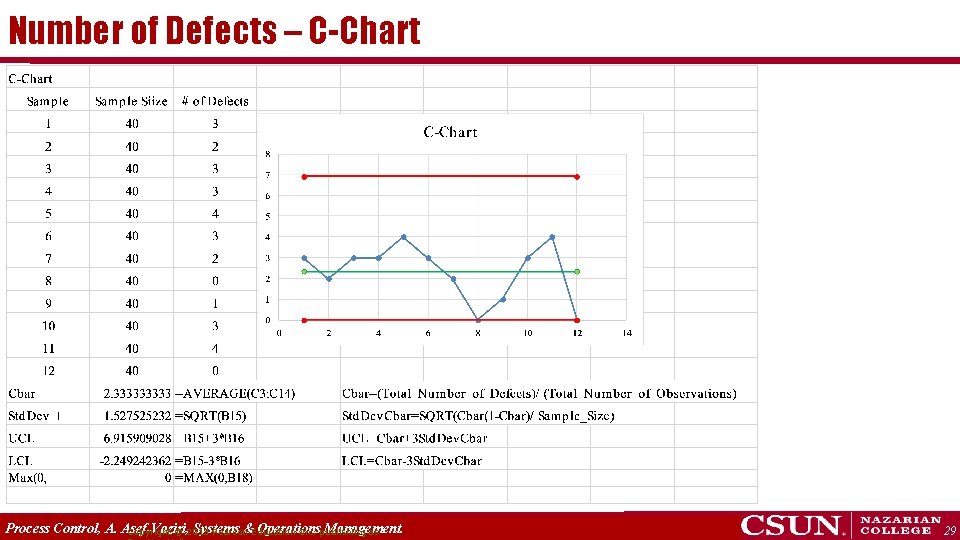
Number of Defects – C-Chart Process Control, A. Asef-Vaziri, Systems &Education Operations Management. Copyright © 2013 Pearson Inc. publishing as 29

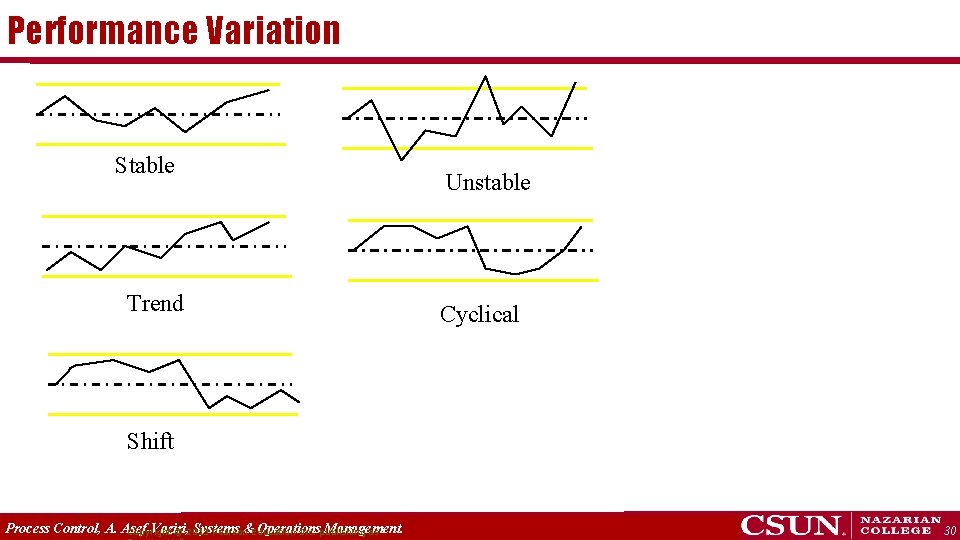
Performance Variation Stable Trend Unstable Cyclical Shift Process Control, A. Asef-Vaziri, Systems &Education Operations Management. Copyright © 2013 Pearson Inc. publishing as 30

Analysis of Variability To analyze and improve variability there are diagnostic tools to help us: 1. Monitor the actual process performance over time 2. Analyze variability in the process 3. Uncover root causes 4. Eliminate those causes 5. Prevent them from recurring in the future Process Control, A. Asef-Vaziri, Systems & Operations Management. 31

The Garage Door Manufacturer Quality planning: Creation of plans for quality, reliability, operations, production, and inspection Quality assurance: Creation and maintenance of the quality system Training: Development, preparation, and maintenance of programs Process Control, A. Asef-Vaziri, Systems & Operations Management. 32

Process Management (Process Planning & Process Control p Process planning’s goal is to produce and deliver products that satisfy targeted customer needs. n n n Structuring the process Designing operating procedures Developing key competencies such as process capability, flexibility, capacity, and cost efficiency p Process control’s goal is to ensure that actual performance conforms to the planned performance. n n Tracking deviations between the actual and the planned performance and taking corrective actions to identify and eliminate sources of these variations. There could be various reasons behind variation in performance. Process Control, A. Asef-Vaziri, Systems & Operations Management. 33

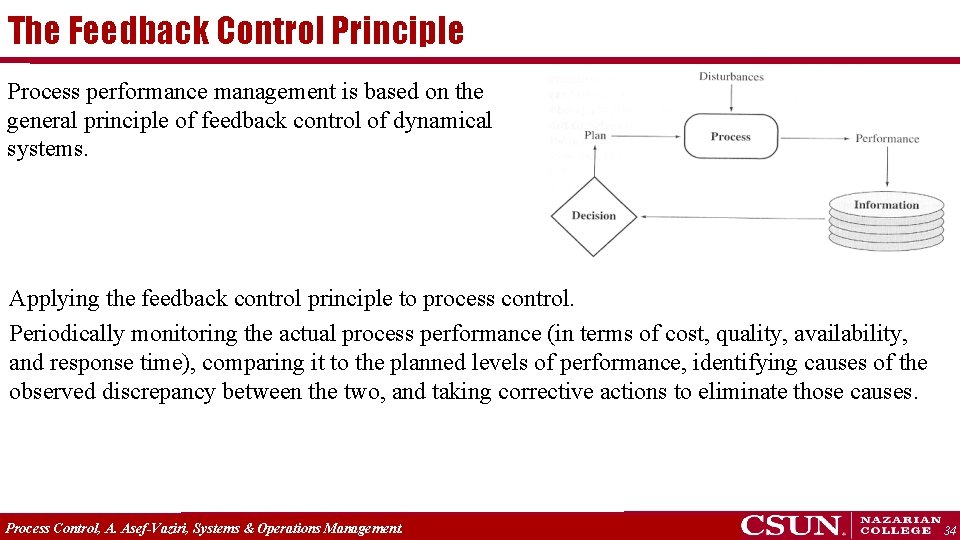
The Feedback Control Principle Process performance management is based on the general principle of feedback control of dynamical systems. Applying the feedback control principle to process control. Periodically monitoring the actual process performance (in terms of cost, quality, availability, and response time), comparing it to the planned levels of performance, identifying causes of the observed discrepancy between the two, and taking corrective actions to eliminate those causes. Process Control, A. Asef-Vaziri, Systems & Operations Management. 34

Plan-Do-Check-Act (PDCA) p Process planning and process control are similar to the Plan-Do-Check-Act (PDCA) cycle. Performed continuously to monitor and improve the process performance. p Problems in Process Control n n n Performance variances are determined by comparison of the current and previous period’s performances. Decisions are based on results of this comparison. Some variances may be due to factors beyond a worker’s control. p According to W. Edward Deming, incentives based on factors that are beyond a worker’s control is like rewarding or punishing workers according to a lottery. Process Control, A. Asef-Vaziri, Systems & Operations Management. 35

Two categories of performance variability p Normal Variability. Is statistically predictable and includes both structural variability and stochastic variability. Cannot be removed easily. Is not in worker’s control. Can be removed only by process re-design, more precise equipment, skilled workers, better material, etc. p Abnormal variability. Unpredictable and disturbs the state of statistical equilibrium of the process by changing parameters of its distribution in an unexpected way. Implies that one or more performance affecting factors may have changed due to external causes or process tampering. Can be identified and removed easily therefore is worker’s responsibility. Process Control, A. Asef-Vaziri, Systems & Operations Management. 36

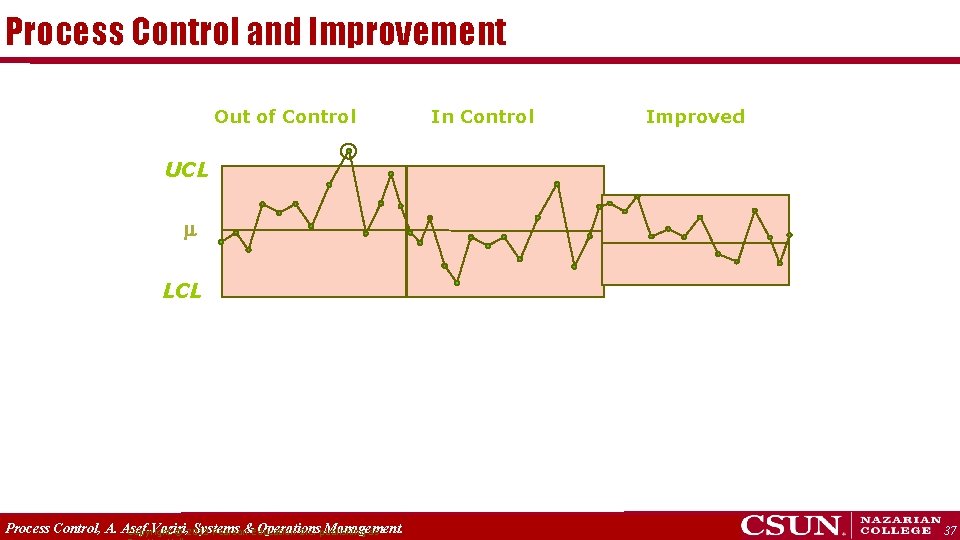
Process Control and Improvement Out of Control In Control Improved UCL LCL Process Control, A. Asef-Vaziri, Systems &Education Operations Management. Copyright © 2013 Pearson Inc. publishing as 37

Control Chart p Continuous Variables: Garage Door Weights, Costs, Waiting Time n Use Normal distribution p Discrete Variables: number of customer complaints, whether a flow unit is defective, number of defects per flow unit produced n Use Binomial or Poisson distribution Process Control, A. Asef-Vaziri, Systems & Operations Management. 38

Cause – Effect Analysis: 5 Why are these doors so heavy? Because the Sheet Metal was too ‘thick’. Why was the sheet metal too thick? Because the rollers at the steel mill were set incorrectly. Why were the rollers set incorrectly? Because the supplier is not able to meet our specifications. Why did we select this supplier? Because our Project Supervisor was too busy getting the product out – didn’t have time to research other vendors. Why did he get himself in this situation? Because he gets paid by meeting the production quotas. Process Control, A. Asef-Vaziri, Systems & Operations Management. 39

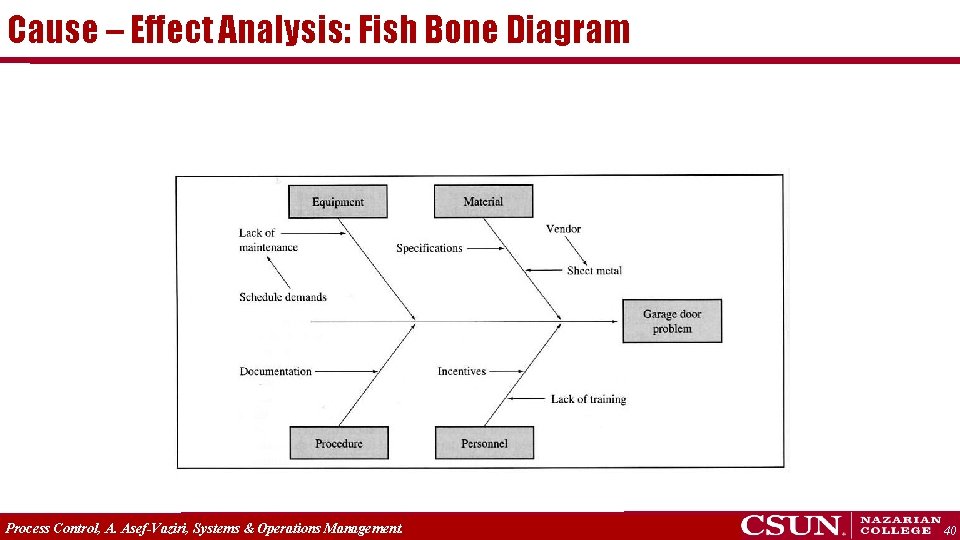
Cause – Effect Analysis: Fish Bone Diagram Process Control, A. Asef-Vaziri, Systems & Operations Management. 40

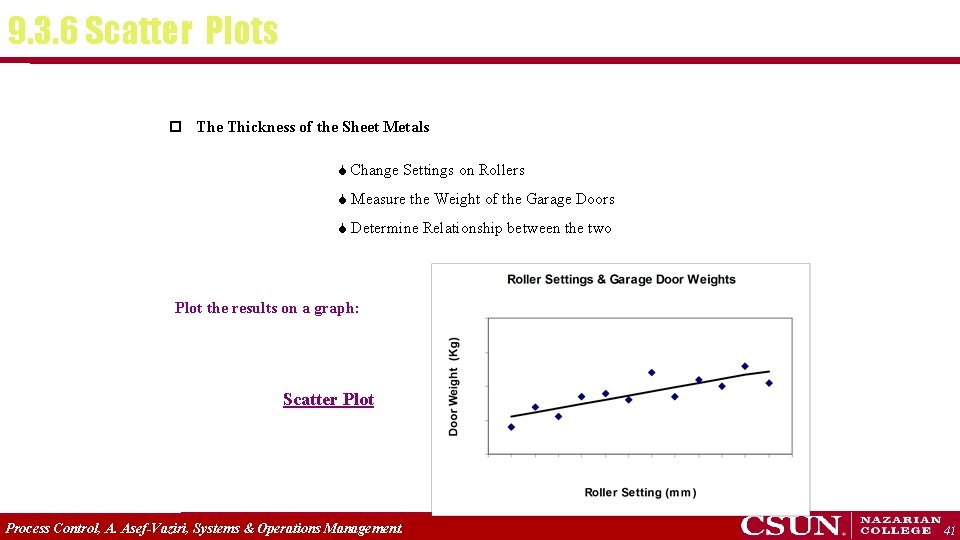
9. 3. 6 Scatter Plots p The Thickness of the Sheet Metals Change Settings on Rollers Measure the Weight of the Garage Doors Determine Relationship between the two Plot the results on a graph: Scatter Plot Process Control, A. Asef-Vaziri, Systems & Operations Management. 41

3 -Sigma & 6 -Sigma Capability p Mean output +/- 3 standard deviations falls within the design specification p It means that 0. 26% of output falls outside the design specification and is unacceptable. p The result: a 3 -sigma capable process produces 2600 defects for every million units produced p Six sigma capability assumes the process is capable of producing output where the mean +/- 6 standard deviations fall within the design specifications p The result: only 3. 4 defects for every million produced p Six sigma capability means smaller variation and therefore higher quality Process Control, A. Asef-Vaziri, Systems & Operations Management. 42

Types of Control Charts Control chart for variables are used to monitor characteristics that can be measured, e. g. length, weight, diameter, time, etc. p Control charts for attributes are used to monitor characteristics that have discrete values and can be counted, e. g. % defective, number of flaws in a shirt, number of broken eggs in a box, etc. p Process Control, A. Asef-Vaziri, Systems & Operations Management. 43

Constructing a X-bar Chart: Process Control, A. Asef-Vaziri, Systems & Operations Management. 44

Xbar Chart Process Control, A. Asef-Vaziri, Systems & Operations Management. 45

Control Charts for Attributes –P-Charts & C-Charts p Use P-Charts for quality characteristics that are discrete and involve yes/no or good/bad decisions n n Percent of leaking caulking tubes in a box of 48 Percent of broken eggs in a carton p Use C-Charts for discrete defects when there can be more than one defect per unit n n Number of flaws or stains in a carpet sample cut from a production run Number of complaints per customer at a hotel Process Control, A. Asef-Vaziri, Systems & Operations Management. 46

Constructing a P-Chart: A Production manager for a tire company has inspected the number of defective tires in five random samples with 20 tires in each sample. The table below shows the number of defective tires in each sample of 20 tires. Sample Size (n) Number Defective 1 20 3 2 20 2 3 20 1 4 20 2 5 20 1 Process Control, A. Asef-Vaziri, Systems & Operations Management. 47

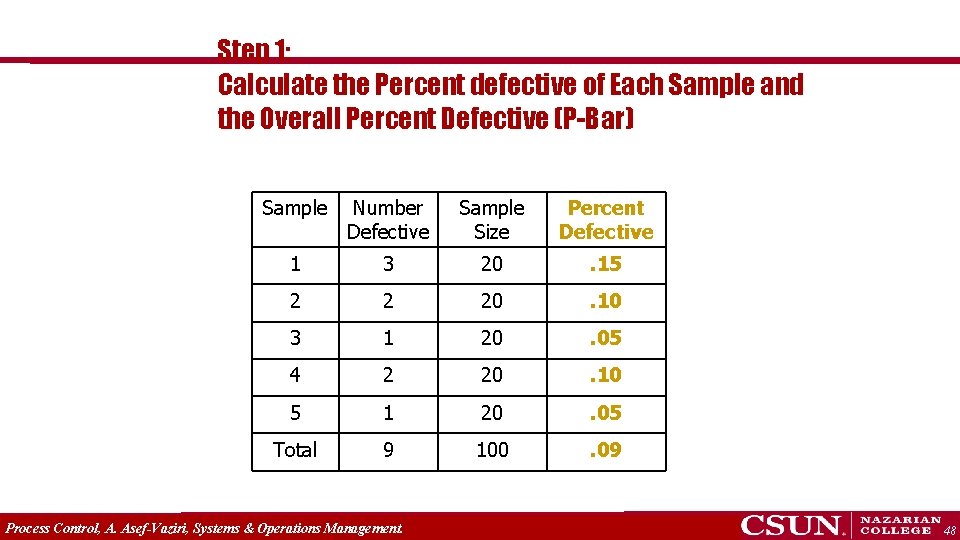
Step 1: Calculate the Percent defective of Each Sample and the Overall Percent Defective (P-Bar) Sample Number Defective Sample Size Percent Defective 1 3 20 . 15 2 2 20 . 10 3 1 20 . 05 4 2 20 . 10 5 1 20 . 05 Total 9 100 . 09 Process Control, A. Asef-Vaziri, Systems & Operations Management. 48

Step 2: Calculate the Standard Deviation of P. Process Control, A. Asef-Vaziri, Systems & Operations Management. 49

Step 3: Calculate CL, UCL, LCL n Center line (p bar): n Control limits for ± 3σ limits: Process Control, A. Asef-Vaziri, Systems & Operations Management. 50

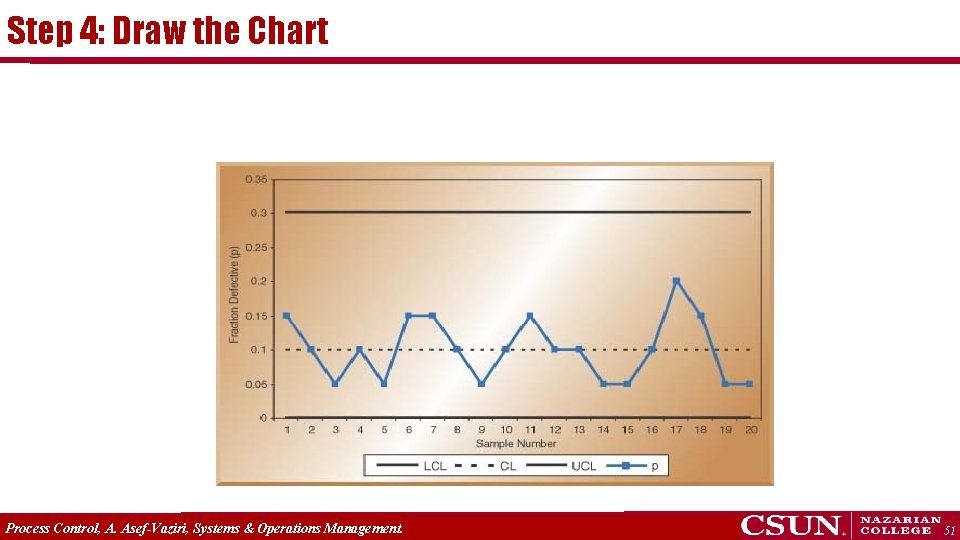
Step 4: Draw the Chart Process Control, A. Asef-Vaziri, Systems & Operations Management. 51

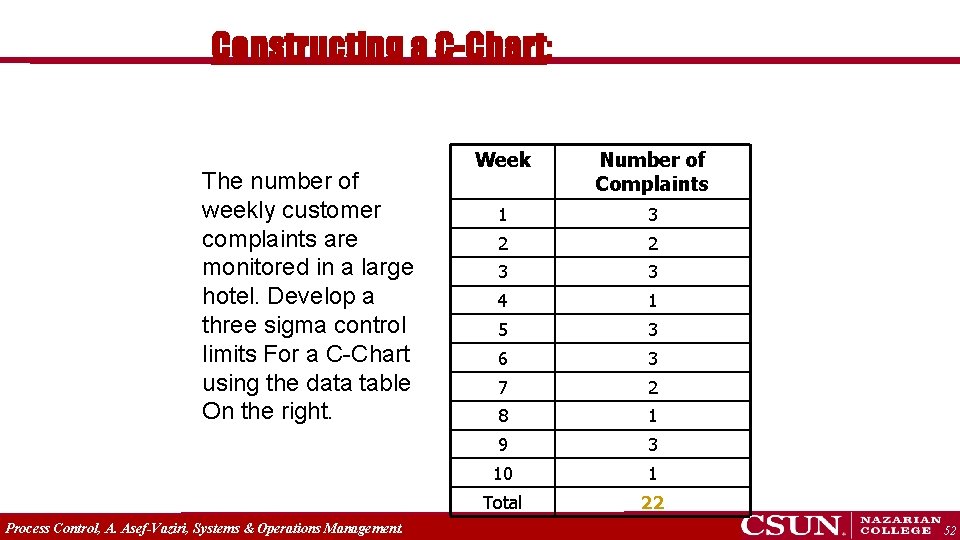
Constructing a C-Chart: The number of weekly customer complaints are monitored in a large hotel. Develop a three sigma control limits For a C-Chart using the data table On the right. Process Control, A. Asef-Vaziri, Systems & Operations Management. Week Number of Complaints 1 3 2 2 3 3 4 1 5 3 6 3 7 2 8 1 9 3 10 1 Total 22 52

Calculate CL, UCL, LCL n Center line (c bar): n Control limits for ± 3σ limits: Process Control, A. Asef-Vaziri, Systems & Operations Management. 53

SQC in Services p Service Organizations have lagged behind manufacturers in the use of statistical quality control p Statistical measurements are required and it is more difficult to measure the quality of a service n Services produce more intangible products n Perceptions of quality are highly subjective p A way to deal with service quality is to devise quantifiable measurements of the service element n Check-in time at a hotel n Number of complaints received per month at a restaurant n Number of telephone rings before a call is answered n Acceptable control limits can be developed and charted Process Control, A. Asef-Vaziri, Systems & Operations Management. 54

Homework Ch. 6 Problems: 1, 4, 6, 7, 8, 10. Process Control, A. Asef-Vaziri, Systems & Operations Management. 55