MANAGERIAL ECONOMICS ECON 5133 Lesson Nine ARC MARGINALS









- Slides: 13

MANAGERIAL ECONOMICS ECON 5133, Lesson Nine ARC MARGINALS Computing difference quotients for a linear function Conclusion for linear functions Copyright © 2005 by George A. Collier Jr.

I. Marginals A. Introduce the math of change 1. Marginals express the rate of change of one variable w. r. t another variable. 2. Ex: speed (mph) expresses the instantaneous rate of change of distance w. r. t. time. P S Click the green loudspeaker to start an audio explanation, the P to pause/restart, or the S to stop the audio.

B. Two types: approximate & true 1. approximate marginal type Termed an “arc marginal” Measures the Average rate of change of one variable w. r. t. another variable total(whatever) Arc M(? ) = another variable a “difference quotient” P S Click the green loudspeaker to start an audio explanation, the P to pause/restart, or the S to stop the audio.

2. The “true” marginal is the Instantaneous rate of change of one variable w. r. t. another variable: change in one variable change in another var. (as this change nears zero) Mathematically: a derivative of a total (? ) w. r. t. another(? ) P S Click the green loudspeaker to start an audio explanation, the P to pause/restart, or the S to stop the audio.

3. both marginal concepts give the same results (if linear functions) Simplify analysis by assigning values B M E EM wish to eliminate. to variables. Ryou ER Ex: Advertising’s influence Let Px = $400, Py = $500 H = 40, 000 I = $20, 000 then Qx = 29000 +. 02 A P S Click the green loudspeaker to start an audio explanation, the P to pause/restart, or the S to stop the audio.

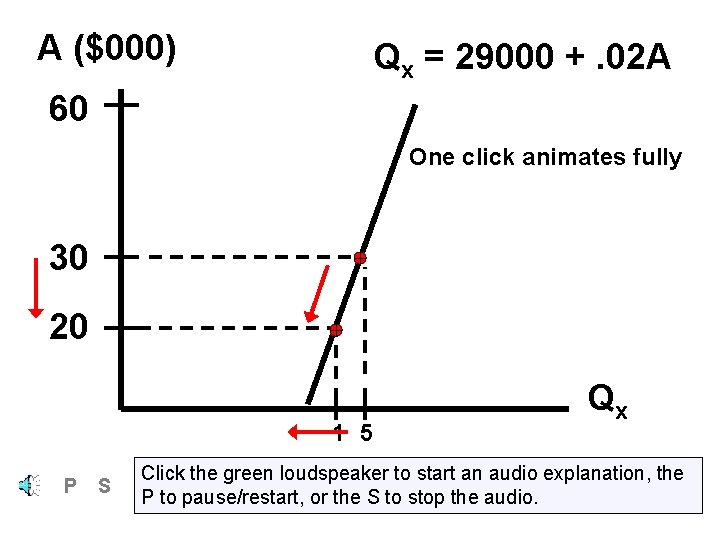
4. consider arc marginal demand w. r. t. advertising expenditures: Qx A Let A range: 20000 A 30000 move 30000 toward 20000, computing a new difference quotient after each move P S Click the green loudspeaker to start an audio explanation, the P to pause/restart, or the S to stop the audio.

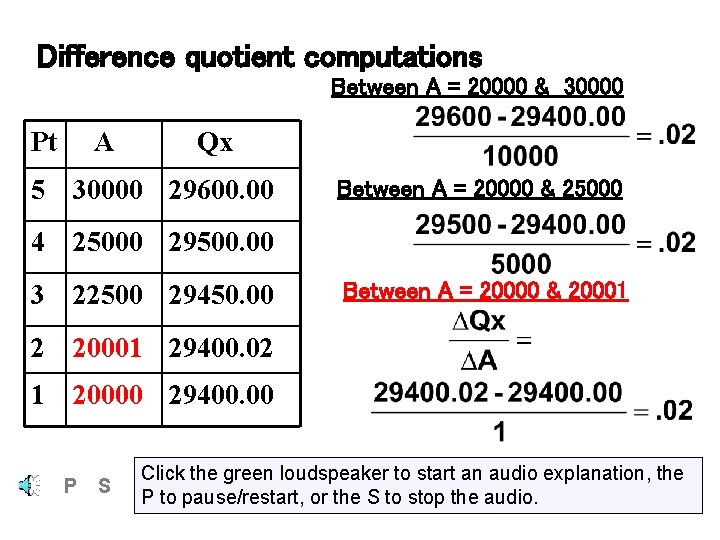
Difference quotient computations (when Qx = 29000 +. 02 A) Pt A Qx Between A = 20000 & 30000 5 30000 29600. 00 4 25000 29500. 00 3 22500 29450. 00 2 20001 29400. 02 1 20000 29400. 00 P S Click the green loudspeaker to start an audio explanation, the P to pause/restart, or the S to stop the audio.

A ($000) Qx = 29000 +. 02 A 60 One click animates fully 30 20 1 5 P S Qx Click the green loudspeaker to start an audio explanation, the P to pause/restart, or the S to stop the audio.

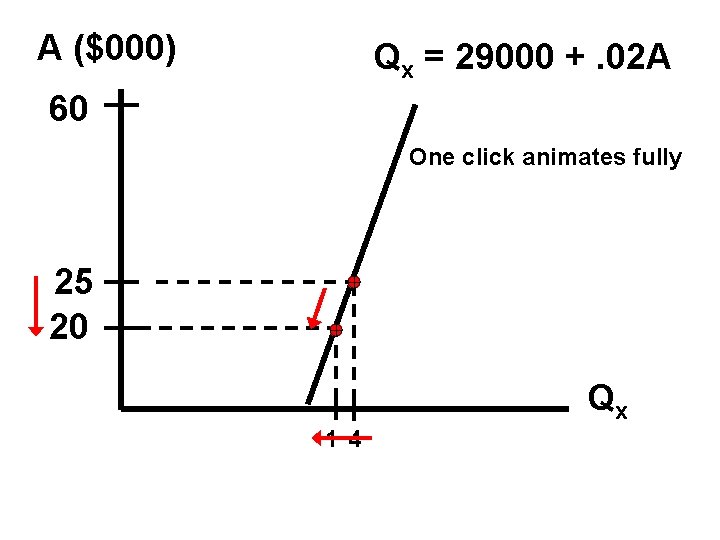
Difference quotient computations Between A = 20000 & 30000 Pt A Qx 5 30000 29600. 00 4 25000 29500. 00 Between A = 20000 & 25000 3 22500 29450. 00 2 20001 29400. 02 1 20000 29400. 00 P S Click the green loudspeaker to start an audio explanation, the P to pause/restart, or the S to stop the audio.

A ($000) Qx = 29000 +. 02 A 60 One click animates fully 25 20 Qx 1 4

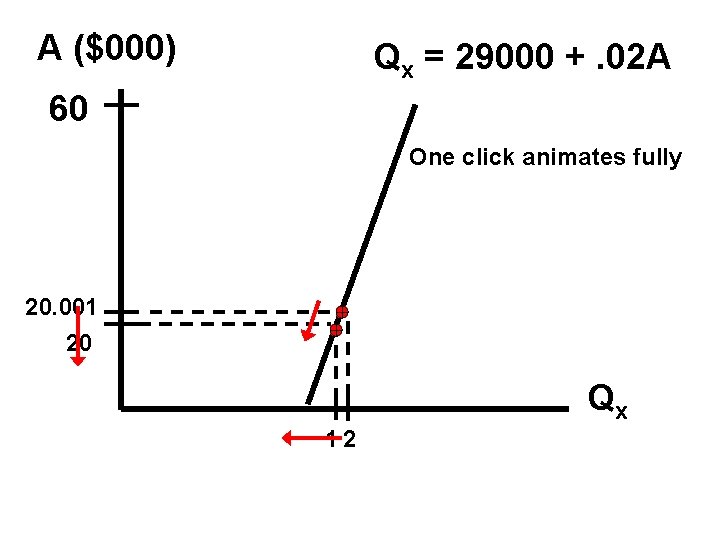
Difference quotient computations Between A = 20000 & 30000 Pt A Qx 5 30000 29600. 00 Between A = 20000 & 25000 4 25000 29500. 00 3 22500 29450. 00 Between A = 20000 & 20001 29400. 02 1 20000 29400. 00 P S Click the green loudspeaker to start an audio explanation, the P to pause/restart, or the S to stop the audio.

A ($000) Qx = 29000 +. 02 A 60 One click animates fully 20. 001 20 Qx 12

5. conclusion (for linear functions) Qx =. 02 (no matter how small A is) Formally stated: limit Qx A 0 A =. 02 calculation is called: “arc marginal advertising” P S Click the green loudspeaker to start an audio explanation, the P to pause/restart, or the S to stop the audio.