Managerial Decision Modeling Cliff Ragsdale 6 edition Chapter

Managerial Decision Modeling Cliff Ragsdale 6. edition Chapter 6 Integer Linear Programming BØK 350 OPERASJONSANALYSE Rasmussen 1

Introduksjon Når en eller flere variabler i et LP problem må anta heltallsverdier har vi et heltallsproblem, Integer Linear Programming (ILP) problem. ILP problemer er ganske vanlige: Fordele arbeidsstyrke Produsere fly Heltallsvariabler gjør oss også i stand til å lage mer nøyaktige modeller for en mengde økonomiske problemer. BØK 350 OPERASJONSANALYSE Rasmussen 2

Heltallsrestriksjoner Max 350 X 1 + 300 X 2 S. T. : Dekningsbidrag 1 X 1 + 1 X 2 <= 200 Pumper 9 X 1 + 6 X 2 <= 1566 Arbeid 16 X 2 2880 Rør 12 X 1 X 2 <= >= 0 Ikke-negativitet Heltallsbetingelser er enkle å angi, men problemet blir ofte mye vanskeligere (og noen ganger umulig) å løse. BØK 350 OPERASJONSANALYSE Rasmussen 3

Forenkling Opprinnelig ILP problem: Forenklet LP problem: Max 2 X 1 + 3 X 2 S. T. : 1 X 1 + 3 X 2 <= 8, 25 2, 5 X 1 + 1 X 2 <= 8, 75 X 1 X 2 >= 0 Heltallsbetingelsene utelates. I forenklingen ser en ganske enkelt bort fra heltallsbetingelsene. BØK 350 OPERASJONSANALYSE Rasmussen 4

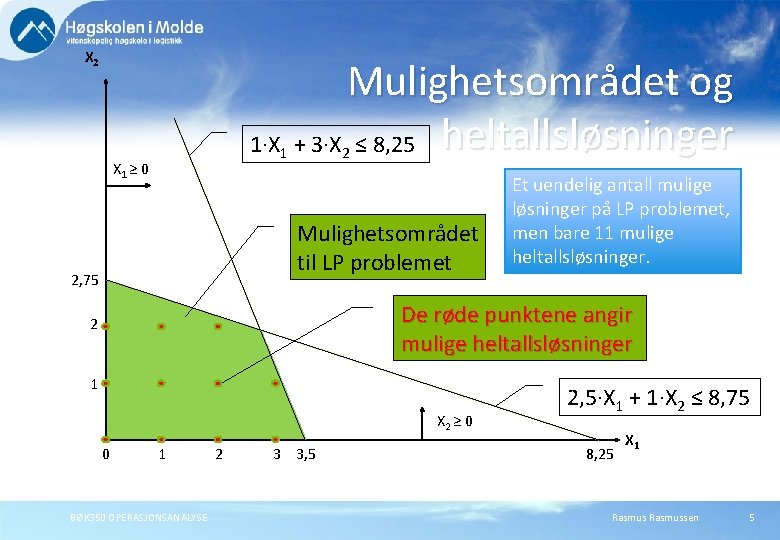
X 2 Mulighetsområdet og 1·X + 3·X ≤ 8, 25 heltallsløsninger 1 X 1 ≥ 0 2 Mulighetsområdet til LP problemet 2, 75 Et uendelig antall mulige løsninger på LP problemet, men bare 11 mulige heltallsløsninger. De røde punktene angir mulige heltallsløsninger 2 1 X 2 ≥ 0 0 1 BØK 350 OPERASJONSANALYSE 2 3 3, 5 2, 5·X 1 + 1·X 2 ≤ 8, 75 8, 25 X 1 Rasmussen 5

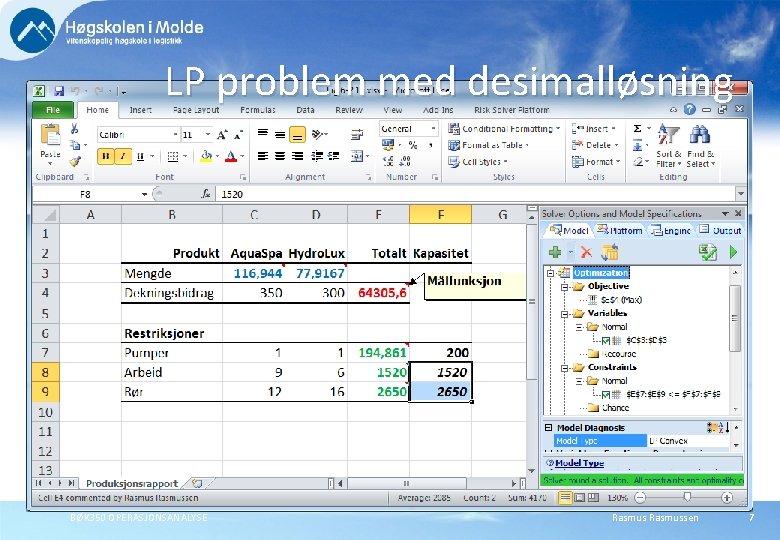
Løsning av ILP problemer Når en løser et LP-forenklet heltallsproblem, kan en noen ganger være heldig å få en optimal heltallsløsning. Det var tilfellet i det opprinnelige Blue Ridge Hot Tubs problemet i tidligere kapitler. Men hva hvis vi reduserer tilgjengelig arbeidstid til 1520 timer og tilgjengelig mengde rør til 2650 dm ? BØK 350 OPERASJONSANALYSE Rasmussen 6

LP problem med desimalløsning BØK 350 OPERASJONSANALYSE Rasmussen 7

Grenser Den optimale løsningen til et LP-forenklet heltallsproblem gir oss en grense for den optimale verdien på målfunksjonen. For maksimerings problemer er den optimale forenklede maksimerings målfunksjonen en øvre grense for den optimale heltallsløsningen. For minimerings problemer er den optimale forenklede minimerings målfunksjonen en nedre grense for den optimale heltallsløsningen. BØK 350 OPERASJONSANALYSE Rasmussen 8

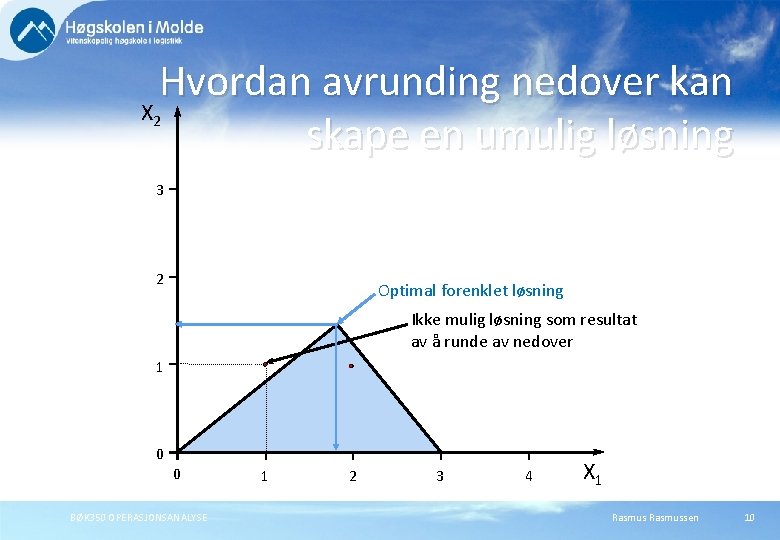
Avrunding Det er fristende å ganske enkelt avrunde en desimalløsning til nærmeste heltallsløsning. Generelt vil dette ikke virke tilfredsstillende: Den avrundede løsningen kan være umulig. Den avrundede løsningen kan være suboptimal. BØK 350 OPERASJONSANALYSE Rasmussen 9

Hvordan avrunding nedover kan X skape en umulig løsning 2 3 2 Optimal forenklet løsning Ikke mulig løsning som resultat av å runde av nedover 1 0 0 BØK 350 OPERASJONSANALYSE 1 2 3 4 X 1 Rasmussen 10

Branch-and-Bound (B&B) algoritmen kan brukes for å løse ILP problemer. Krever løsning av en serie med LP problemer kalt ”kandidat problemer”. Teoretisk kan dette løse et hvilket som helst ILP. I praksis krever det ofte enormt mye regnekraft (og tid). BØK 350 OPERASJONSANALYSE Rasmussen 11

Stoppe - regler Fordi B&B tar så lang tid, tillater de fleste ILP pakker å angi en suboptimalitets toleranse faktor. Den lar deg stoppe straks en heltallsløsning er funnet som er innenfor en gitt % av den globale optimale løsningen. Grenser oppnådd fra LP-forenklingen er her nyttige. F. eks. LP forenklingen har optimal verdi på målfunksjonen lik $64. 306. 95% av $64. 306 er $61. 090. En heltallsløsning med verdi på målfunksjonen lik $61. 090 eller må derfor ligge innenfor 5% av den optimale løsningen. BØK 350 OPERASJONSANALYSE Rasmussen 12

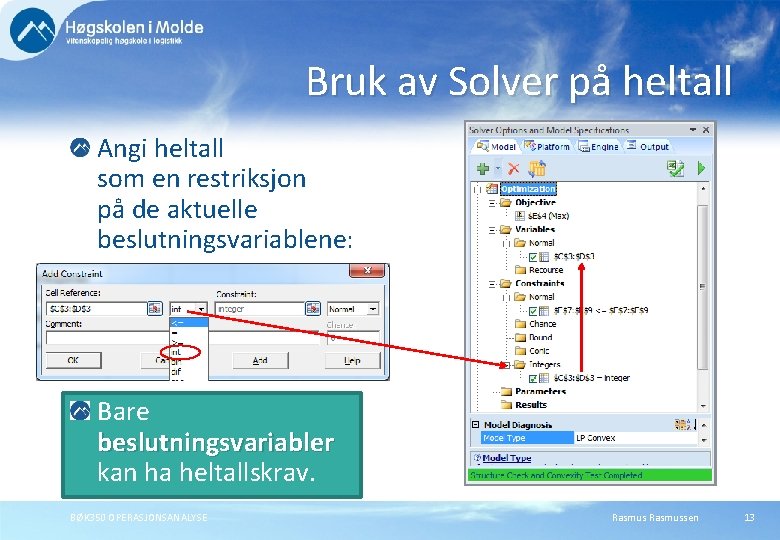
Bruk av Solver på heltall Angi heltall som en restriksjon på de aktuelle beslutningsvariablene: Bare beslutningsvariabler kan ha heltallskrav. BØK 350 OPERASJONSANALYSE Rasmussen 13

Integer Tolerance Under Engine tab i Task Pane, Integer Tolerance. I den nye Solver (V 9 osv. ) er standard Integer Tolerance = 0 Forbedret B&B algoritmer (strong branching) gjør at Solver raskere finner gode heltallsløsninger. BØK 350 OPERASJONSANALYSE Rasmussen 14

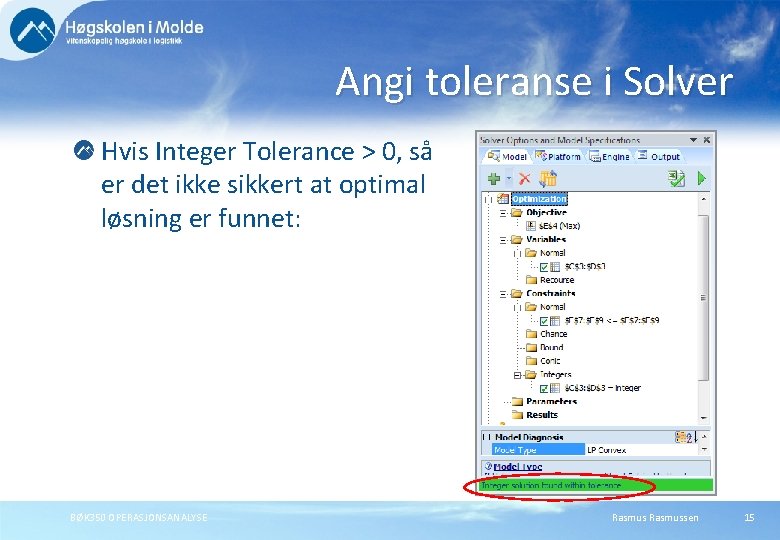
Angi toleranse i Solver Hvis Integer Tolerance > 0, så er det ikke sikkert at optimal løsning er funnet: BØK 350 OPERASJONSANALYSE Rasmussen 15

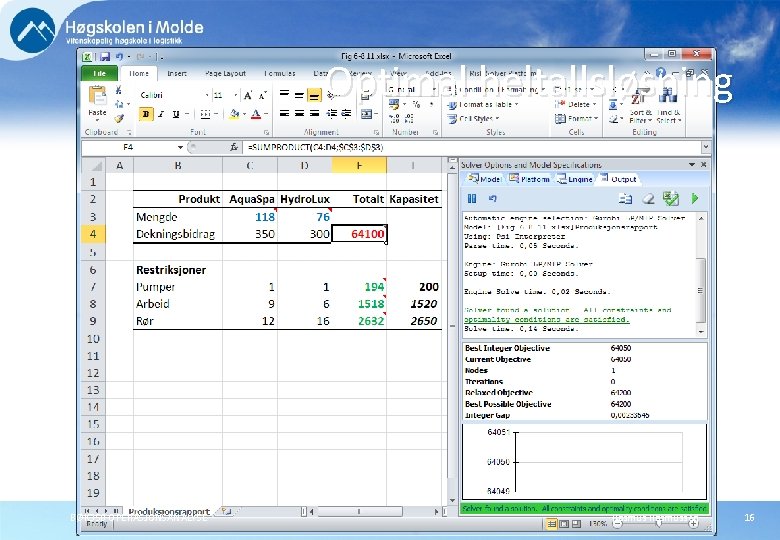
Optimal heltallsløsning BØK 350 OPERASJONSANALYSE Rasmussen 16

Et skiftplanleggingsproblem: Dag Behov Skift 1 Skift 2 Skift 3 Skift 4 Skift 5 Skift 6 Skift 7 Mandag 27 Fri Tirsdag 22 Onsdag 26 Torsdag 25 Fredag 21 Lørdag 19 Søndag 18 Fri Lønn 680 Fri Fri Fri 705 705 680 655 Behovet for antall ansatte varierer med ukedagene. Lønn pr. ansatt pr. uke er lavest for de som har fri i helgene (lørdag og søndag). BØK 350 OPERASJONSANALYSE Rasmussen 17

Definer beslutningsvariablene X 1 = antall arbeidere tildelt skift 1 X 2 = antall arbeidere tildelt skift 2 X 3 = antall arbeidere tildelt skift 3 X 4 = antall arbeidere tildelt skift 4 X 5 = antall arbeidere tildelt skift 5 X 6 = antall arbeidere tildelt skift 6 X 7 = antall arbeidere tildelt skift 7 BØK 350 OPERASJONSANALYSE Rasmussen 18

Definer målfunksjonen Lønnen er $131 pr. dag, med tillegg $25 pr. dag for helg (lørdag og søndag). De som jobber 5 ukedager har ukelønn 131 5 = 655 De som i tillegg jobber en helgedag har 655 + 25 = 680 De som jobber to helgedager har 655 + 25 2 = 705. Minimer totale lønnskostnader: MIN: 680 X 1 +705 X 2 +705 X 3 +705 X 4 +705 X 5 +680 X 6 +655 X 7 BØK 350 OPERASJONSANALYSE Rasmussen 19

Definere restriksjonene Behov for arbeidere hver ukedag: 0 X 1 + 0 X 2 + 1 X 3 + 1 X 4 + 1 X 5 + 1 X 6 + 1 X 7 >= 27 } Mandag 1 X 1 + 0 X 2 + 0 X 3 + 1 X 4 + 1 X 5 + 1 X 6 + 1 X 7 >= 22 } Tirsdag 1 X 1 + 1 X 2 + 0 X 3 + 0 X 4 + 1 X 5 + 1 X 6 + 1 X 7 >= 26 } Onsdag 1 X 1 + 1 X 2 + 1 X 3 + 0 X 4 + 0 X 5 + 1 X 6 + 1 X 7 >= 25 } Torsdag 1 X 1 + 1 X 2 + 1 X 3 + 1 X 4 + 0 X 5 + 0 X 6 + 1 X 7 >= 21 } Fredag 1 X 1 + 1 X 2 + 1 X 3 + 1 X 4 + 1 X 5 + 0 X 6 + 0 X 7 >= 19 } Lørdag 0 X 1 + 1 X 2 + 1 X 3 + 1 X 4 + 1 X 5 + 1 X 6 + 0 X 7 >= 18 } Søndag Ikke-negativitets-betingelsene: Xi >= 0 for alle i BØK 350 OPERASJONSANALYSE Rasmussen 20

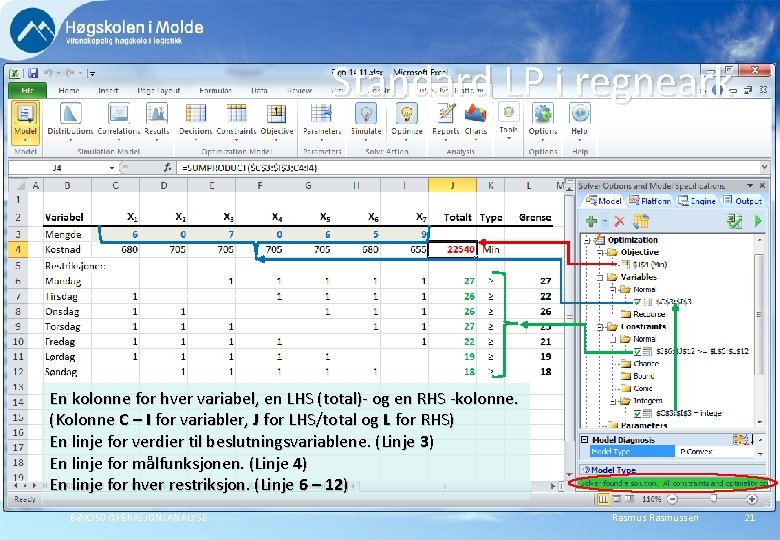
Standard LP i regneark En kolonne for hver variabel, en LHS (total)- og en RHS -kolonne. (Kolonne C – I for variabler, J for LHS/total og L for RHS) En linje for verdier til beslutningsvariablene. (Linje 3) En linje for målfunksjonen. (Linje 4) En linje for hver restriksjon. (Linje 6 – 12) BØK 350 OPERASJONSANALYSE Rasmussen 21

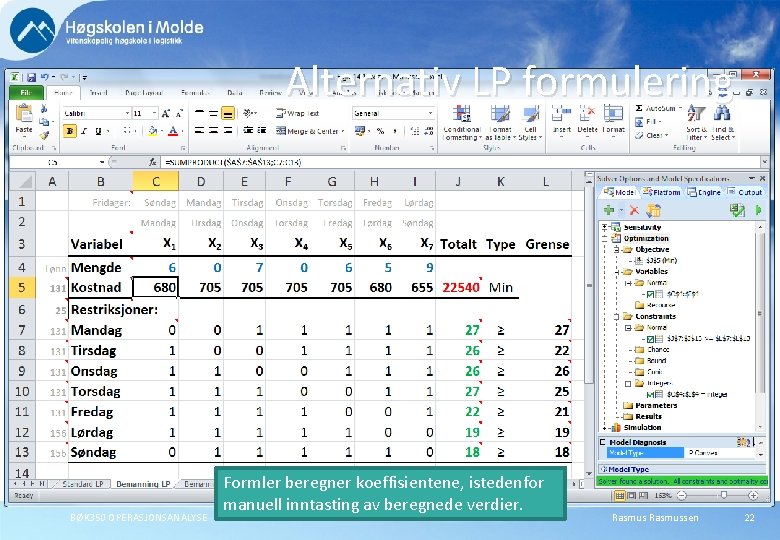
Alternativ LP formulering BØK 350 OPERASJONSANALYSE Formler beregner koeffisientene, istedenfor manuell inntasting av beregnede verdier. Rasmussen 22

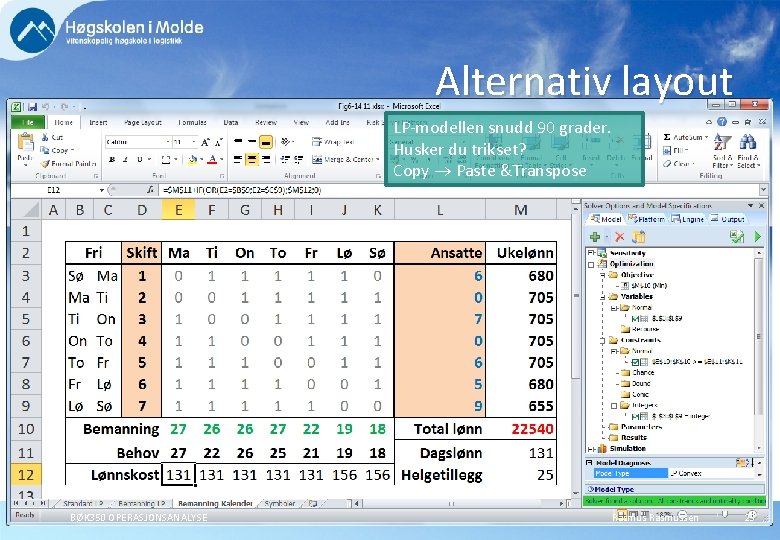
Alternativ layout LP-modellen snudd 90 grader. Husker du trikset? Copy Paste &Transpose BØK 350 OPERASJONSANALYSE Rasmussen 23

Binær -variabler Binære variabler er heltallsvariabler som bare kan anta to verdier: 0 eller 1 Slike variabler kan være meget nyttige i en mengde praktiske modelleringssituasjoner. BØK 350 OPERASJONSANALYSE Rasmussen 24

Et kapitalbudsjetteringsproblem: Forventet NPV Prosjekt (i $000) 1 $141 2 $187 3 $121 4 $83 5 $265 6 $127 Kapital (i $000) som trengs i År 1 År 2 År 3 År 4 $75 $20 $15 $90 $35 $0 $0 $60 $15 $15 $30 $20 $10 $5 $100 $25 $20 $50 $20 $10 $30 År 5 $10 $30 $15 $5 $20 $40 Selskapet har $250, 000 disponibelt år 1 til å investere i nye prosjekter. Det har budsjettert $75, 000 til fornyet dekning til disse prosjektene i år 2. Og det er budsjettert inntil $50, 000 per år for årene 3, 4, og 5. BØK 350 OPERASJONSANALYSE Rasmussen 25

Definere beslutningsvariablene Vi kan altså investere i prosjektene 1 – 6, men bare i hele prosjekter. Vi kan heller ikke investere i mer enn ett prosjekt av samme type, dvs. prosjektene kan ikke dupliseres. BØK 350 OPERASJONSANALYSE Rasmussen 26

Definere målfunksjonen Maksimer total netto nåverdi av de valgte prosjektene. MAX: 141 X 1 + 187 X 2 + 121 X 3 + 83 X 4 + 265 X 5 + 127 X 6 Merk at de prosjektene som ikke velges «nulles» ut. BØK 350 OPERASJONSANALYSE Rasmussen 27

Definere restriksjonene Kapitalrestriksjoner 75 X 1 + 90 X 2 + 60 X 3 + 30 X 4 + 100 X 5 + 50 X 6 <= 250} år 1 25 X 1 + 35 X 2 + 15 X 3 + 20 X 4 + 25 X 5 + 20 X 6 <= 75} år 2 20 X 1 + 0 X 2 + 15 X 3 + 10 X 4 + 20 X 5 + 10 X 6 <= 50} år 3 15 X 1 + 0 X 2 + 15 X 3 + 5 X 4 + 20 X 5 + 30 X 6 <= 50} år 4 10 X 1 + 30 X 2 + 15 X 3 + 5 X 4 + 20 X 5 + 40 X 6 <= 50} år 5 Binærrestriksjoner Xi <= 1, i = 1, 2, . . . , 6 Xi >= 0, i = 1, 2, . . . , 6 Alle Xi må være heltall BØK 350 OPERASJONSANALYSE Rasmussen 28

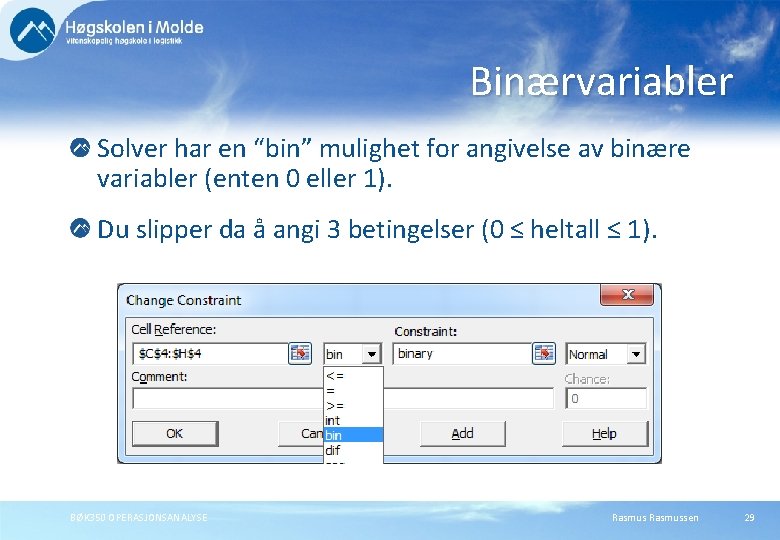
Binærvariabler Solver har en “bin” mulighet for angivelse av binære variabler (enten 0 eller 1). Du slipper da å angi 3 betingelser (0 ≤ heltall ≤ 1). BØK 350 OPERASJONSANALYSE Rasmussen 29

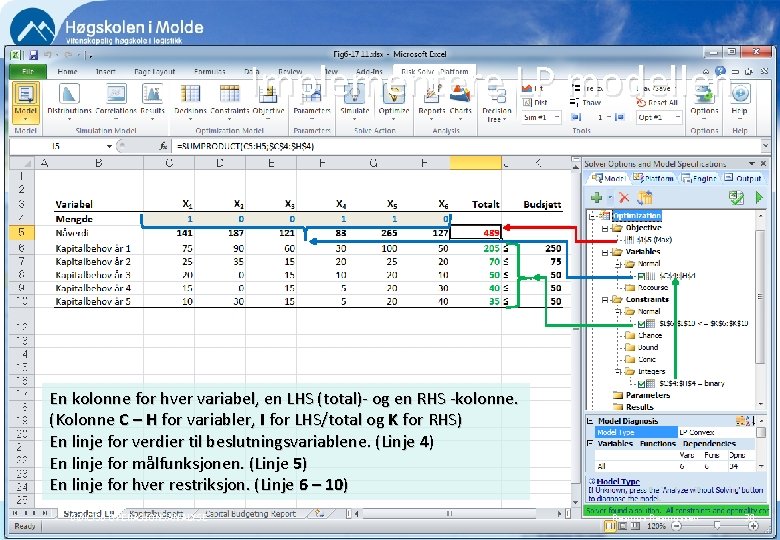
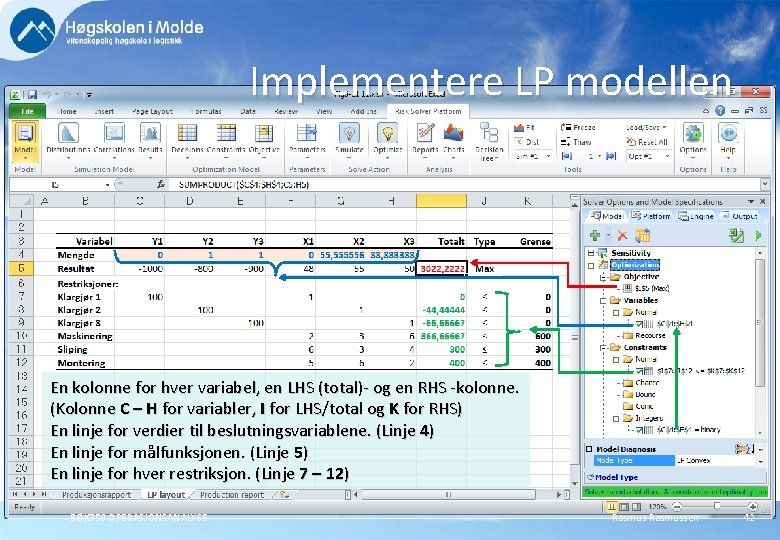
Implementere LP modellen En kolonne for hver variabel, en LHS (total)- og en RHS -kolonne. (Kolonne C – H for variabler, I for LHS/total og K for RHS) En linje for verdier til beslutningsvariablene. (Linje 4) En linje for målfunksjonen. (Linje 5) En linje for hver restriksjon. (Linje 6 – 10) BØK 350 OPERASJONSANALYSE Rasmussen 30

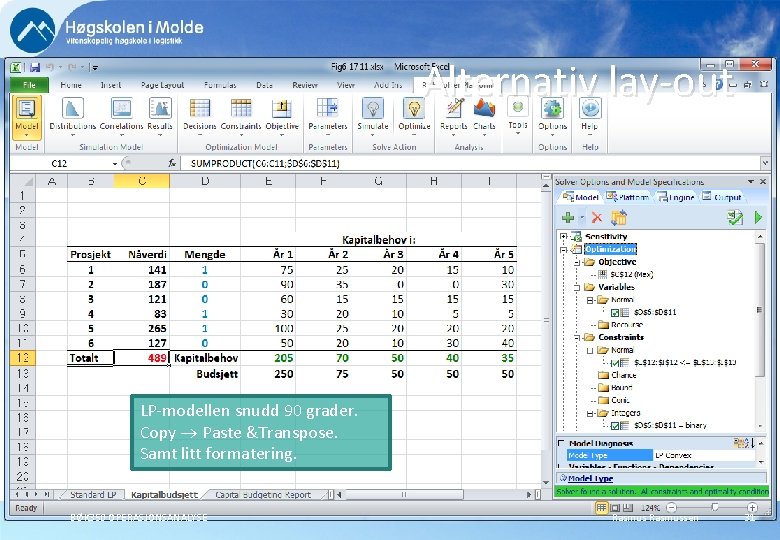
Alternativ lay-out LP-modellen snudd 90 grader. Copy Paste &Transpose. Samt litt formatering. BØK 350 OPERASJONSANALYSE Rasmussen 31

Binære Variabler & Logiske Betingelser Binære variabler er også nyttige ved modellering av en rekke logiske betingelser. Av prosjektene 1, 3 & 6, kan maksimalt ett velges: X 1 + X 3 + X 6 <= 1 Av prosjektene 1, 3 & 6, må nøyaktig ett velges: X 1 + X 3 + X 6 = 1 Prosjekt 4 kan ikke velges med mindre også prosjekt 5 velges: X 4 <= X 5 eller X 4 – X 5 <= 0 BØK 350 OPERASJONSANALYSE Rasmussen 32

Faste kostnader Mange beslutninger medfører at faste kostnader endres: l l Kostnad ved leasing, leie eller kjøp av utstyr som kreves hvis et spesielt alternativ velges. Klargjøringskostnader som er nødvendige for å forberede en maskin eller et produksjonsutstyr til å produsere en annen type produkt. Kostnaden ved å konstruere nytt produksjonsutstyr som kreves hvis en bestemt beslutning fattes. Kostnader ved å ansette mer personale som vil bli nødvendig hvis en bestemt beslutning tas. BØK 350 OPERASJONSANALYSE Rasmussen 33

Eksempel med faste kostnader : Operasjon Prod. 1 Prod. 2 Prod. 3 Maskinering 2 3 6 Sliping 6 3 4 Montering 5 6 2 DB pr. Stk. $48 $55 $50 Klargjøringskost $1000 $800 $900 Timer tilgjengelig 600 300 400 Tabellen viser produktenes tidsforbruk og tilgjengelig tid i de tre produksjonsavdelingene. Den viser også produktenes dekningsbidrag pr. stk, samt klargjøringskostnader før en produksjonsserie. BØK 350 OPERASJONSANALYSE Rasmussen 34

Definere beslutningsvariablene Yi angir om vi har klargjort til produksjon av produkt Xi. Yi = binærvariabel. Xi = kvantum av produkt i som skal produseres, i = 1, 2, 3 Xi = standard kontinuerlig variabel (delbar, ikke-negativ). BØK 350 OPERASJONSANALYSE Rasmussen 35

Definere målfunksjonen Maksimere total fortjeneste: MAX: – 1000 Y 1 – 800 Y 2 – 900 Y 3 + 48 X 1 + 55 X 2 + 50 X 3 Faste klargjøringskostnader oppstår når binærvariablene Yi = 1. BØK 350 OPERASJONSANALYSE Rasmussen 36

Definere restriksjonene Ressursrestriksjoner 2 X 1 + 3 X 2 + 6 X 3 <= 600 6 X 1 + 3 X 2 + 4 X 3 <= 300 5 X 1 + 6 X 2 + 2 X 3 <= 400 } maskinering } sliping } montering Binær-restriksjoner Yi <= 1, i = 1, 2, 3 Yi >= 0, i = 1, 2, 3 Alle Yi må være heltall Ikke-negativitetsrestriksjoner Xi >= 0, i = 1, 2, 3 BØK 350 OPERASJONSANALYSE Er det noe som mangler? Rasmussen 37

Definere restriksjonene (forts. ) Koble restriksjonene (med “Big M”) X 1 <= M 1 Y 1 eller X 1 - M 1 Y 1 <= 0 X 2 <= M 2 Y 2 eller X 2 - M 2 Y 2 <= 0 X 3 <= M 3 Y 3 eller X 3 - M 3 Y 3 <= 0 Hvis Yi = 0 så vil disse restriksjonene tvinge Xi til å bli lik 0. Hvis Yi = 1 så tillater disse restriksjonene Xi å være 0 eller større. Men hvis Xi = 0 vil målsettingen da medføre at også Yi settes til 0, for å spare kostnader. Merk at Mi angir en øvre grense for Xi. Vi må velge en tilstrekkelig stor men ikke for stor verdi til Mi. BØK 350 OPERASJONSANALYSE Rasmussen 38

Finne rimelige verdier for M 1 Betrakt ressursrestriksjonene 2 X 1 + 3 X 2 + 6 X 3 <= 600 6 X 1 + 3 X 2 + 4 X 3 <= 300 5 X 1 + 6 X 2 + 2 X 3 <= 400 } maskinering } sliping } montering Hva er maksimum verdi X 1 kan anta? La X 2 = X 3 = 0 X 1 = MIN(600/2, 300/6, 400/5) = MIN(300, 50, 80) = 50 Maximum verdier for X 2 & X 3 kan finnes på samme måte. BØK 350 OPERASJONSANALYSE Rasmussen 39

Sammendrag av modellen MAX: - 1000 Y 1 - 800 Y 2 - 900 Y 3 + 48 X 1 + 55 X 2 + 50 X 3 Slik at: 2 X 1 + 3 X 2 + 6 X 3 <= 600 6 X 1 + 3 X 2 + 4 X 3 <= 300 5 X 1 + 6 X 2 + 2 X 3 <= 400 X 1 <= 50 Y 1 X 2 <= 67 Y 2 X 3 <= 75 Y 3 Yi <= 1, i = 1, 2, 3 Yi >= 0, i = 1, 2, 3 Alle Yi må være heltall Xi >= 0, i = 1, 2, 3 BØK 350 OPERASJONSANALYSE } maskinering } sliping } montering kobling binær-restriksjoner } ikke-negativitet Rasmussen 40

Mulige feller Ikke bruk IF( ) funksjonen til å modellere IF( ) sammenhengen mellom Xi og Yi. Anta celle A 5 representerer X 1 Anta celle A 6 representerer Y 1 Du ønsker å lage A 6 = IF(A 5>0; 1; 0) Dette vil skape store problemer for Solver! La Yi være som en hvilken som helst variabel. Gjør dem til binære beslutningsvariabler. Bruk koblingsrestriksjoner til å skape de nødvendige sammenhengene mellom Xi og Yi. BØK 350 OPERASJONSANALYSE Rasmussen 41

Implementere LP modellen En kolonne for hver variabel, en LHS (total)- og en RHS -kolonne. (Kolonne C – H for variabler, I for LHS/total og K for RHS) En linje for verdier til beslutningsvariablene. (Linje 4) En linje for målfunksjonen. (Linje 5) En linje for hver restriksjon. (Linje 7 – 12) BØK 350 OPERASJONSANALYSE Rasmussen 42

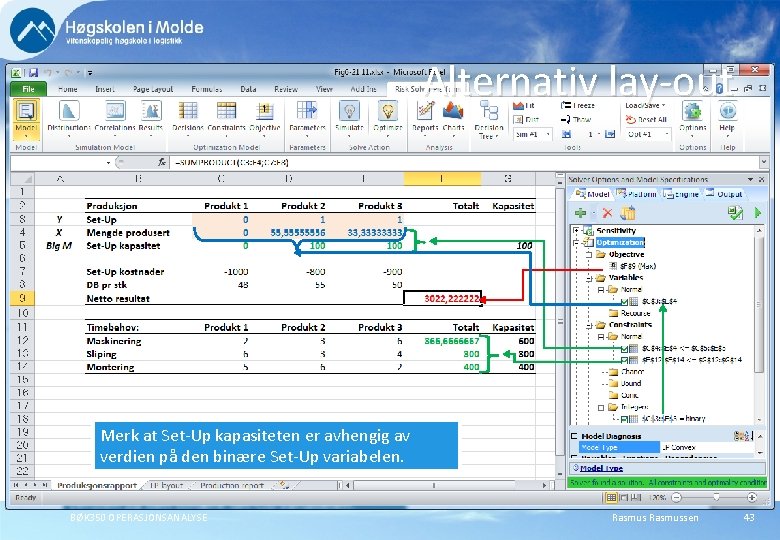
Alternativ lay-out Merk at Set-Up kapasiteten er avhengig av verdien på den binære Set-Up variabelen. BØK 350 OPERASJONSANALYSE Rasmussen 43

Minimum ordre størrelse Anta at Remington ikke ønsker å produsere noe av produkt 3 uten at det blir produsert minst 40 enheter. Vurder følgende: X 3 <= M 3 Y 3 X 3 >= 40 Y 3 BØK 350 OPERASJONSANALYSE Rasmussen 44

Kvantumsrabatter Max 350 X 1 + 300 X 2 S. T. : Dekningsbidrag 1 X 1 + 1 X 2 <= 200 Pumper 9 X 1 + 6 X 2 <= 1566 Arbeid 16 X 2 <= 2880 Rør >= 0 Og heltall 12 X 1 X 2 Kvantumsrabatter: Ved produksjon over 75 stk. X 1 oppnås rabatter slik at dekningsbidraget økes til 375$ pr. enhet. Ved produksjon over 50 stk. X 2 oppnås rabatter slik at dekningsbidraget økes til 325$ pr. enhet. BØK 350 OPERASJONSANALYSE Rasmussen 45

LP modell med rabatter Uten rabatt Med rabatt Max 350 X 1 U + 375 X 1 M + 300 X 2 U + 325 X 2 M S. T. : Dekningsbidrag 1 X 1 U + 1 X 1 M + 1 X 2 U + 1 X 2 M <= 200 Pumper 9 X 1 U + 9 X 1 M + 6 X 2 U + 6 X 2 M <= 1566 Arbeid 12 X 1 U + 12 X 1 M + 16 X 2 U + 16 X 2 M <= 2880 Rør I tillegg må vi ha følgende betingelser: X 1 M <= M 1 MY 1 M } kan ikke produsere med rabatt X 1 U >= 75 Y 1 M } før vi ha produsert 75 uten. X 2 M <= M 2 MY 2 M } kan ikke produsere med rabatt X 2 U >= 50 Y 2 M } før vi ha produsert 50 uten. Y 1 M, Y 2 M binærvariabler; Xij ikke-negative heltall. BØK 350 OPERASJONSANALYSE Rasmussen 46

Revidert LP modell med rabatter Max S. T. : 350 X 1 U + 375 X 1 M + 300 X 2 U + 325 X 2 M Dekningsbidrag 1 X 1 U + 1 X 1 M + 1 X 2 U + 1 X 2 M <= 200 Pumper 9 X 1 U + 9 X 1 M + 6 X 2 U + 6 X 2 M <= 1566 Arbeid 12 X 1 U + 12 X 1 M + 16 X 2 U + 16 X 2 M <= 2880 Rør X 1 U X 1 M -75 Y 1 M >= 0 -200 Y 1 M <= 0 -50 Y 2 M >= 0 -200 Y 2 M <= 0 >= 0 X 2 U X 2 M X 1 U X 1 M X 2 U X 2 M Y 1 M BØK 350 OPERASJONSANALYSE Y 2 M Og heltall Binærvariabler Rasmussen 47

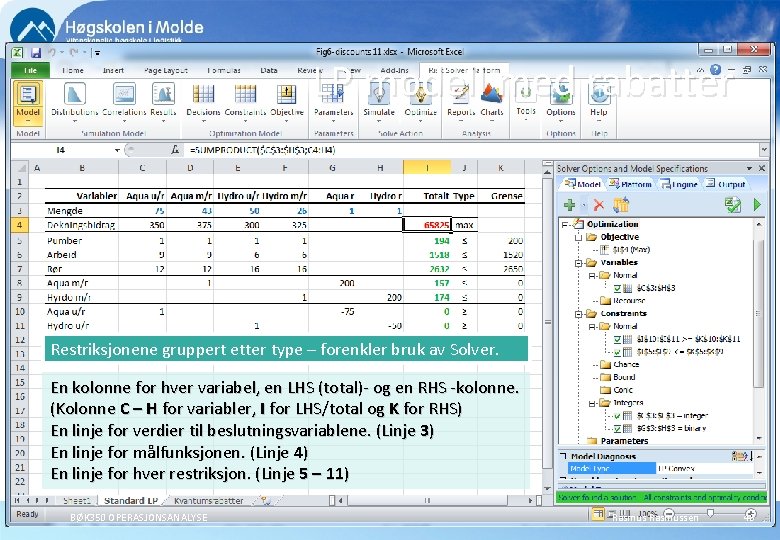
LP modell med rabatter Restriksjonene gruppert etter type – forenkler bruk av Solver. En kolonne for hver variabel, en LHS (total)- og en RHS -kolonne. (Kolonne C – H for variabler, I for LHS/total og K for RHS) En linje for verdier til beslutningsvariablene. (Linje 3) En linje for målfunksjonen. (Linje 4) En linje for hver restriksjon. (Linje 5 – 11) BØK 350 OPERASJONSANALYSE Rasmussen 48

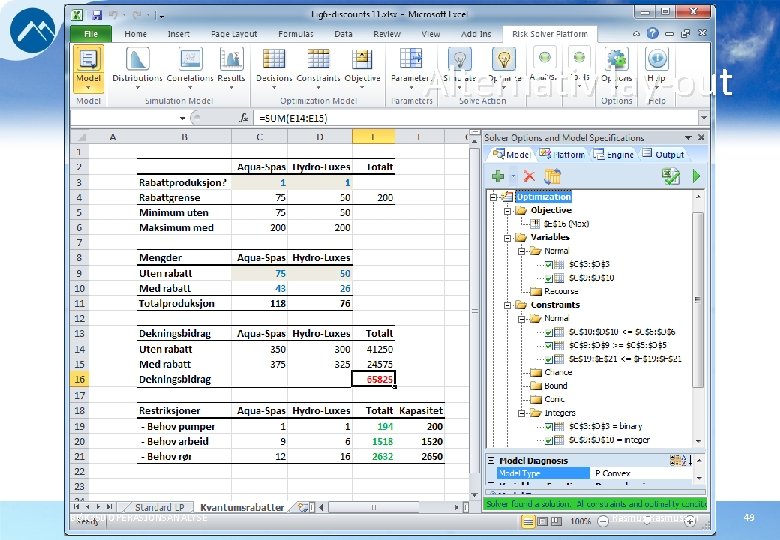
Alternativ lay-out BØK 350 OPERASJONSANALYSE Rasmussen 49

Et kontraktstildelingsproblem: Selskap 1 2 3 Behov Kostnad pr levert tonn sement Prosjekt 1 Prosjekt 2 Prosjekt 3 Prosjekt 4 $120 $115 $130 $125 $100 $150 $110 $105 $140 $95 $145 $165 450 tonn 275 tonn 300 tonn 350 tonn Kapasitet 525 tonn 450 tonn 550 tonn Selskap 1 leverer bare ordrer på minst 150 tonn. Selskap 2 kan levere ordrer på over 200 tonn bare for ett prosjekt. Selskap 3 leverer totalt bare i kvanta på 200, 400 eller 550 tonn. BØK 350 OPERASJONSANALYSE Rasmussen 50

Definere beslutningsvariablene Xij = tonn sement kjøpt fra selskap i til prosjekt j i = 1, 2, 3; j = 1, 2, 3, 4 BØK 350 OPERASJONSANALYSE Rasmussen 51

Definere målfunksjonen Minimere totale kostnader: MIN: 120 X 11 + 115 X 12 + 130 X 13 + 125 X 14 + 100 X 21 + 150 X 22 + 110 X 23 + 105 X 24 + 140 X 31 + 95 X 32 + 145 X 33 + 165 X 34 BØK 350 OPERASJONSANALYSE Rasmussen 52

Definere restriksjonene Kapasitetsrestriksjoner X 11 + X 12 + X 13 + X 14 <= 525 X 21 + X 22 + X 23 + X 24 <= 450 X 31 + X 32 + X 33 + X 34 <= 550 } Selskap 1 } Selskap 2 } Selskap 3 Etterspørselsrestriksjoner X 11 + X 21 + X 31 = 450 X 12 + X 22 + X 32 = 275 X 13 + X 23 + X 33 = 300 X 14 + X 24 + X 34 = 350 } Prosjekt 1 } Prosjekt 2 } Prosjekt 3 } Prosjekt 4 Ikke-negativitetsrestriksjoner Xij >= 0, i = 1, 2, 3; j = 1, 2, 3, 4 BØK 350 OPERASJONSANALYSE Rasmussen 53

Definere restriksjonene (forts. ) Selskap 1 leverer bare ordrer på minst 150 tonn X 1 j <= 525 Y 1 j X 1 j >= 150 Y 1 j j = 1, 2, 3, 4 Selskap 2 kan levere over 200 tonn bare for ett prosjekt X 2 j <= 200 + 250 Y 2 j j = 1, 2, 3, 4 Y 21 + Y 22 + Y 23 + Y 24 <= 1 Selskap 3 leverer totalt bare 200, 400 eller 550 tonn X 31 + X 32 + X 33 + X 34 = 200 Y 31 + 400 Y 32 + 550 Y 33 Y 31 + Y 32 + Y 33 <= 1 BØK 350 OPERASJONSANALYSE Rasmussen 54

Sammendrag av modellen MIN: 120 X 11 + 115 X 12 + 130 X 13 + 125 X 14 + 100 X 21 + 150 X 22 + 110 X 23 + 105 X 24 + 140 X 31 + 95 X 32 + 145 X 33 + 165 X 34 slik at: X 11 + X 12 + X 13 + X 14 <= 525 X 21 + X 22 + X 23 + X 24 <= 450 X 31 + X 32 + X 33 + X 34 <= 550 X 11 + X 21 + X 31 = 450 X 12 + X 22 + X 32 = 275 X 13 + X 23 + X 33 = 300 X 14 + X 24 + X 34 = 350 BØK 350 OPERASJONSANALYSE } Selskap 1 } Selskap 2 } Selskap 3 } Prosjekt 1 } Prosjekt 2 } Prosjekt 3 } Prosjekt 4 Rasmussen 55

Sammendrag av modellen (forts. ) X 1 j <= 525 Y 1 j j = 1, 2, 3, 4 X 1 j >= 150 Y 1 j j = 1, 2, 3, 4 X 2 j <= 200 + 250 Y 2 j j = 1, 2, 3, 4 Y 21 + Y 22 + Y 23 + Y 24 <= 1 X 31 + X 32 + X 33 + X 34 = 200 Y 31 + 400 Y 32 + 550 Y 33 Y 31 + Y 32 + Y 33 <= 1 Xij >= 0, i = 1, 2, 3; j = 1, 2, 3, 4 Yij =binær-variabel; i = 1, 2, 3; j = 1, 2, 3, 4 BØK 350 OPERASJONSANALYSE Rasmussen 56

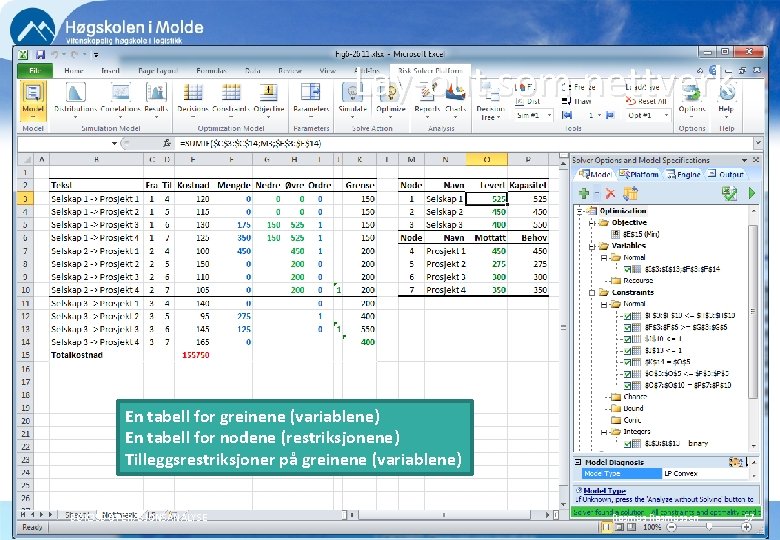
Lay-out som nettverk En tabell for greinene (variablene) En tabell for nodene (restriksjonene) Tilleggsrestriksjoner på greinene (variablene) BØK 350 OPERASJONSANALYSE Rasmussen 57

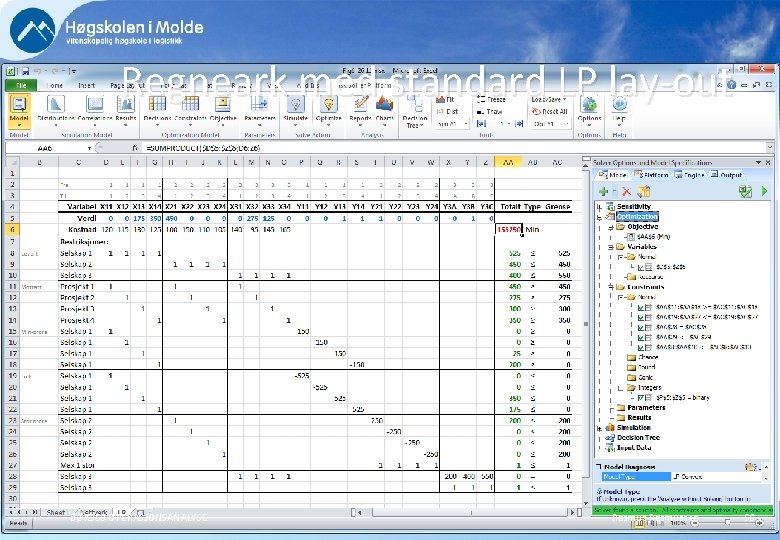
Regneark med standard LP lay-out BØK 350 OPERASJONSANALYSE Rasmussen 58

Branch-And-Bound algoritmen Opprinnelig ILP problem: Max 2 X 1 + 3 X 2 S. T. : 1 X 1 + 3 X 2 <= 8, 25 2, 5 X 1 + 1 X 2 <= 8, 75 X 1 X 2 BØK 350 OPERASJONSANALYSE >= 0 Heltall Rasmussen 59

X 2 Mulighetsområdet og 1·X + 3·X ≤ 8, 25 heltallsløsninger 1 2 Optimal Relaxed løsning X 1 = 2, 769, X 2=1, 826 Målfunksjon = 11, 019 2, 75 2 1 2, 5·X 1 + 1·X 2 ≤ 8, 75 0 1 BØK 350 OPERASJONSANALYSE 2 3 3, 5 8, 25 X 1 Rasmussen 60

Branch-And-Bound algoritmen Problem I: Problem II: Max 2 X 1 + 3 X 2 S. T. : 1 X 1 + 3 X 2 <= 8, 25 2, 5 X 1 + 1 X 2 <= 8, 75 X 1 <= 2 X 1 >= 3 X 1 >= 0 X 2 X 1 X 2 BØK 350 OPERASJONSANALYSE Heltall X 2 X 1 X 2 Heltall Rasmussen 61

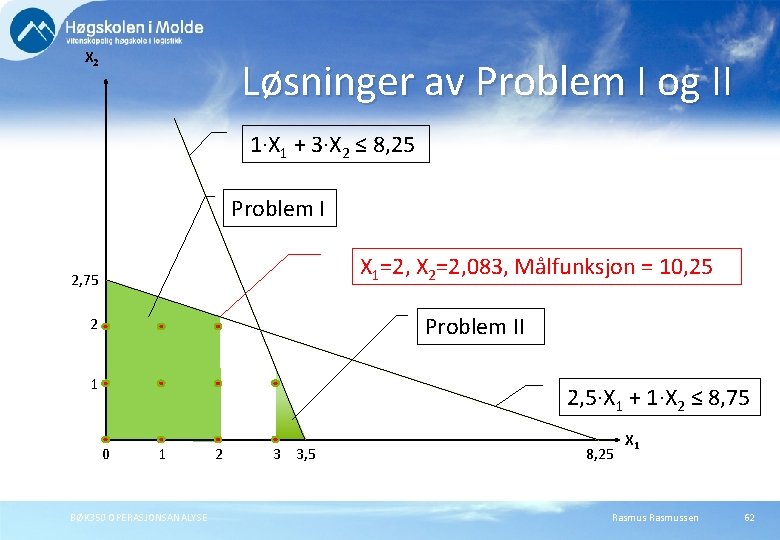
X 2 Løsninger av Problem I og II 1·X 1 + 3·X 2 ≤ 8, 25 Problem I X 1=2, X 2=2, 083, Målfunksjon = 10, 25 2, 75 Problem II 2 1 2, 5·X 1 + 1·X 2 ≤ 8, 75 0 1 BØK 350 OPERASJONSANALYSE 2 3 3, 5 8, 25 X 1 Rasmussen 62

Branch-And-Bound algoritmen Problem III: Problem IV: Max 2 X 1 + 3 X 2 S. T. : 1 X 1 + 3 X 2 <= 8, 25 2, 5 X 1 + 1 X 2 <= 8, 75 X 1 X 2 BØK 350 OPERASJONSANALYSE <= 2 >= 0 Heltall Max 2 X 1 + 3 X 2 S. T. : 1 X 1 + 3 X 2 <= 8, 25 2, 5 X 1 + 1 X 2 <= 8, 75 X 1 X 2 <= 2 >= 3 >= 0 Heltall Rasmussen 63

X 2 Løsninger av Problem II og III 1·X 1 + 3·X 2 ≤ 8, 25 Problem III X 1=2, X 2=2, Målfunksjon = 10 2, 75 X 1=3, X 2=1, 25, Målfunksjon = 9, 75 2 Problem II 1 2, 5·X 1 + 1·X 2 ≤ 8, 75 0 1 BØK 350 OPERASJONSANALYSE 2 3 3, 5 8, 25 X 1 Rasmussen 64

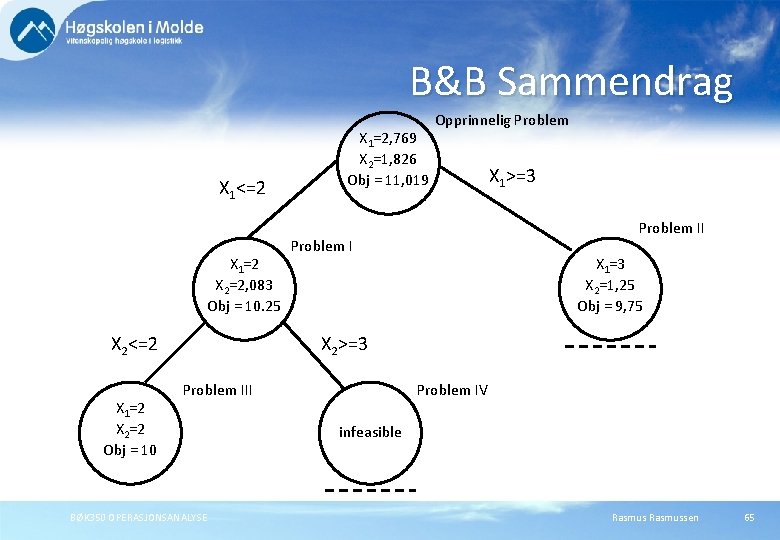
B&B Sammendrag X 1<=2 X 1=2 X 2=2, 083 Obj = 10. 25 X 2<=2 X 1=2 X 2=2 Obj = 10 X 1=2, 769 X 2=1, 826 Obj = 11, 019 Opprinnelig Problem X 1>=3 Problem II Problem I X 1=3 X 2=1, 25 Obj = 9, 75 X 2>=3 Problem III BØK 350 OPERASJONSANALYSE Problem IV infeasible Rasmussen 65

Slutt på kapittel 6 BØK 350 OPERASJONSANALYSE Rasmussen 66