Management Information System Comprehensive and Organized Chapter 1

Management Information System Comprehensive and Organized Chapter 1 Data, Information and System

Chapter Highlights • Data, Information and System • Attributes of Information Quality • System and category • Management function wise application of IS • System integration • IS resources • Computing categories • Number system • Logic gates

Data, Information and System • Data is the representation of concepts or other entities, fixed in or on a medium in a form suitable for communication, interpretation, or processing by human beings or by automated systems • Data is a symbol set that is qualified or quantified • Data is defined as a body of facts or figures gathered systematically for one or more specific purposes

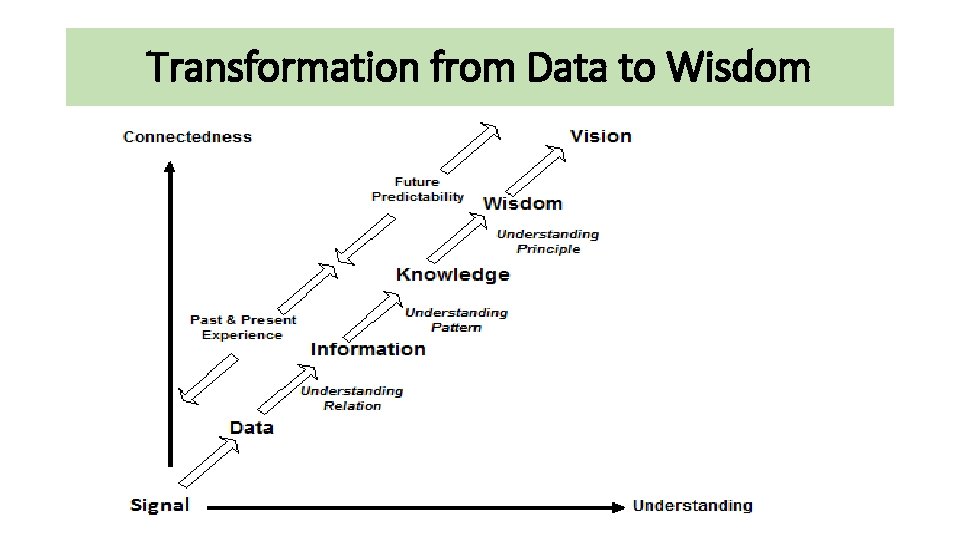
Transformation from Data to Wisdom

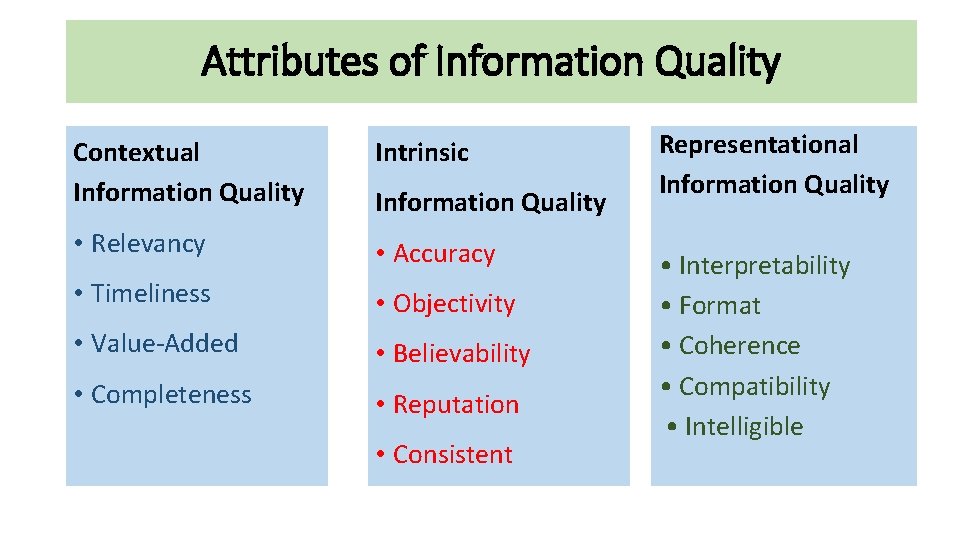
Attributes of Information Quality Contextual Information Quality Intrinsic • Relevancy • Accuracy • Timeliness • Objectivity • Value-Added • Believability • Completeness • Reputation Information Quality • Consistent Representational Information Quality • Interpretability • Format • Coherence • Compatibility • Intelligible

System and its Category • Open System & Closed System • Stationary and non-stationary • Conceptual and Empirical • Subsystems and super systems • Social, People-Machine & Machine • Adaptive and Non adaptive System • Natural and Manufactured • Deterministic System and probabilistic system • Permanent and temporary

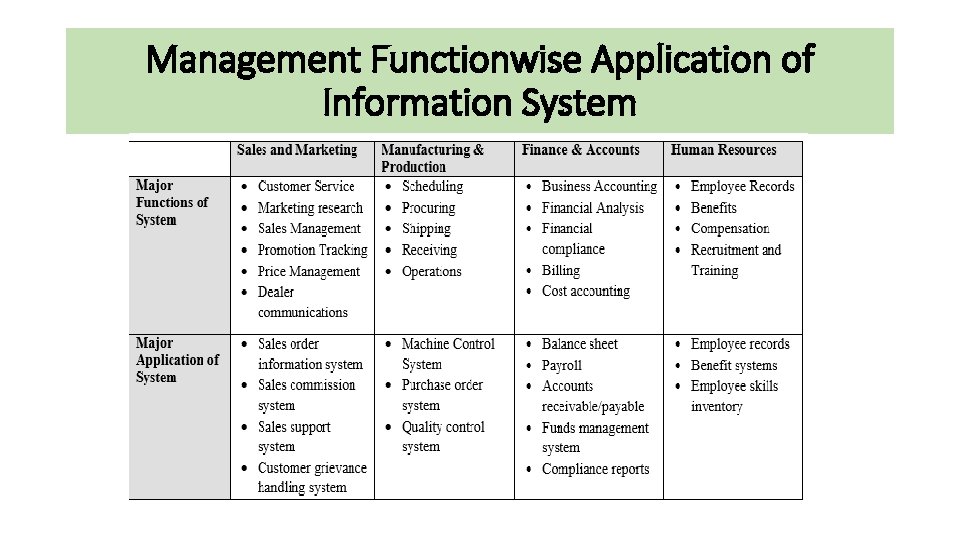
Management Functionwise Application of Information System

System Integration Vertical Integration • Subsystems are integrated according to their functionality by creating "silos" of functional entities, beginning with the bottom basic function upward (vertical). • For example, integration of financial, marketing, production and HR subsystems is vertical integration. Horizontal Integration • Also known as Enterprise Service Bus (ESB). • Here, a specialized subsystem is focused on communication between the remaining subsystems. • An enterprise service bus (ESB) implements a communication system between mutually interacting software applications in a service-oriented architecture (SOA).

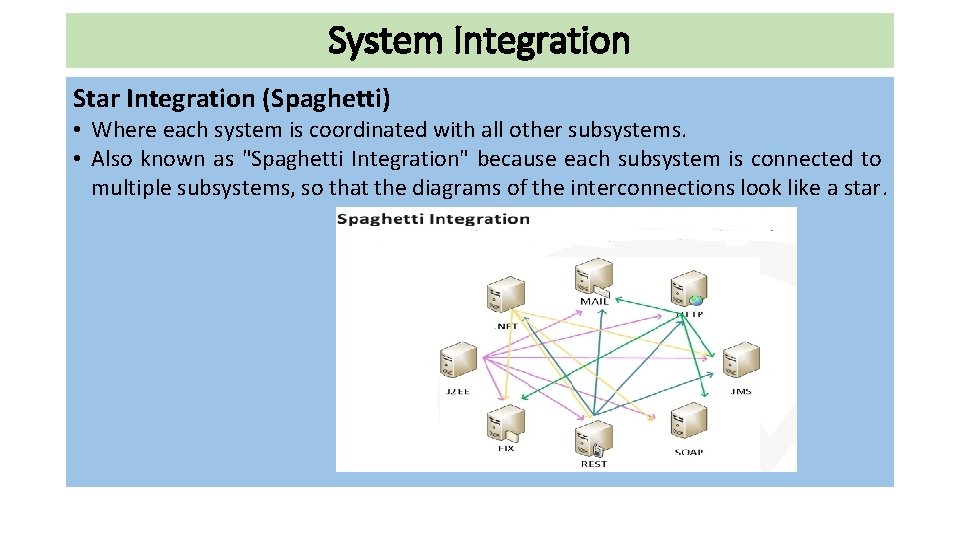
System Integration Star Integration (Spaghetti) • Where each system is coordinated with all other subsystems. • Also known as "Spaghetti Integration" because each subsystem is connected to multiple subsystems, so that the diagrams of the interconnections look like a star.

Information System Resources Hardware Resources • Server, Desktop, Laptop, i. Pad, Smartphone, Printer, Plotter, Scanner, Primary and Secondary Storage devices Software Resources • Systems software, Application software (including tools Middleware, Groupware), Programming language. Data Resources • Forms and Reports, Text/Numeric Data Files, Video and Audio files, Database, Messages Network Resources • Bridge, Switch, Routers, Firewall, Hub, Cables Human Resources • Project Manager, System analyst, Application Architect, Programmer, Tester, Data entry operator

Computing Categories • Hard computing, i. e. , conventional computing requires a precisely stated analytical model and often a lot of computation time. Many analytical models are valid for ideal cases. Real world problems exist in a non-ideal environment. The premises and guiding principles of hard Computing are precision, certainty, and rigor. • Many contemporary problems do not lend themselves to precise solutions such as recognition problems (handwriting, speech, objects, images, mobile robot coordination, forecasting etc. This is where soft computing comes to its rescue. • Soft computing differs from conventional (hard) computing in that, unlike hard computing, it is tolerant of imprecision, uncertainty, partial truth, and approximation. In effect, the role model for soft computing is the human mind. The principal constituents, i. e. , tools, techniques, of Soft Computing are: • • • Fuzzy Logic Neural Networks Support Vector Machines Evolutionary Computation Machine Learning and Probabilistic Reasoning

Number System Decimal System • The number system used commonly is the decimal number system. • Decimal number system has base 10 as it uses 10 digits from 0 to 9. Example of Decimal System (5× 1000) + (6× 100) + (7× 10) + (8× 1) (5× 103) + (6 × 102) + (7 × 101) + (8 × 100) 5000 + 600 + 70 + 8 5678

Number System Binary Numeral System – Base-2 In base two, the columns or “places” for 20 = 1, 21 = 2, 22 = 4, 23 = 8, 24 = 16, and so forth. Binary Number 23 = 8; 22 = 4; 21= 2; 20= 1 Decimal Equivalent 0001 (0× 23) + (0× 22) + (0× 21) + (1× 20) 1 0010 (0× 23) + (0× 22) + (1× 21) + (0× 20) 2 0011 (0× 23) + (0× 22) + (1× 21) + (1× 20) 3 0100 (0× 23) + (1× 22) + (0× 21) + (0× 20) 4 0101 (0× 23) + (1× 22) + (0× 21) + (1× 20) 5 0110 (0× 23) + (1× 22) + (1× 21) + (0× 20) 6 0111 (0× 23) + (1× 22) + (1× 21) + (1× 20) 7 1000 (1× 23) + (0× 22) + (0× 21) + (0× 20) 8 1001 (1× 23) + (0× 22) + (0× 21) + (1× 20) 9 1010 (1× 23) + (0× 22) + (1× 21) + (0× 20) 10

Binary Arithmetic – Binary Addition Binary addition works in the same way, except that only 0’s and 1’s can be used, instead of the whole spectrum of 0 -9. This actually makes binary addition much simpler than decimal addition, as we only need to remember the following: Rules of Binary Addition 0+0=0 0+1=1 1+0=1 1 + 1 = 0 and carry 1 to the next significant digit As an example of binary addition we have, Binary Decimal 1 1 (Carry) 00011010 26 00001100 +12 -----------00100110 38

Boolean Algebra and Logic Gate • Boolean algebra is the foundation of the digital (logic) circuits. • It uses only the binary numbers i. e. 0 and 1, better known as Binary Algebra or logical Algebra. Boolean algebra was invented by George Boole in 1854. Rules in Boolean Algebra Following are the important rules used in Boolean algebra. • Variable used can have only two values. • Binary 1 for HIGH and Binary 0 for LOW. • Complement of a variable is represented by an overbar (-). • Thus, complement of variable B is represented as • ORing of the variables is represented by a plus (+) sign between them. For example ORing of A, B, C is represented as A + B + C. • Logical ANDing of the two or more variable is represented by writing a dot between them such as A. B. C. Sometime the dot may be omitted like ABC.

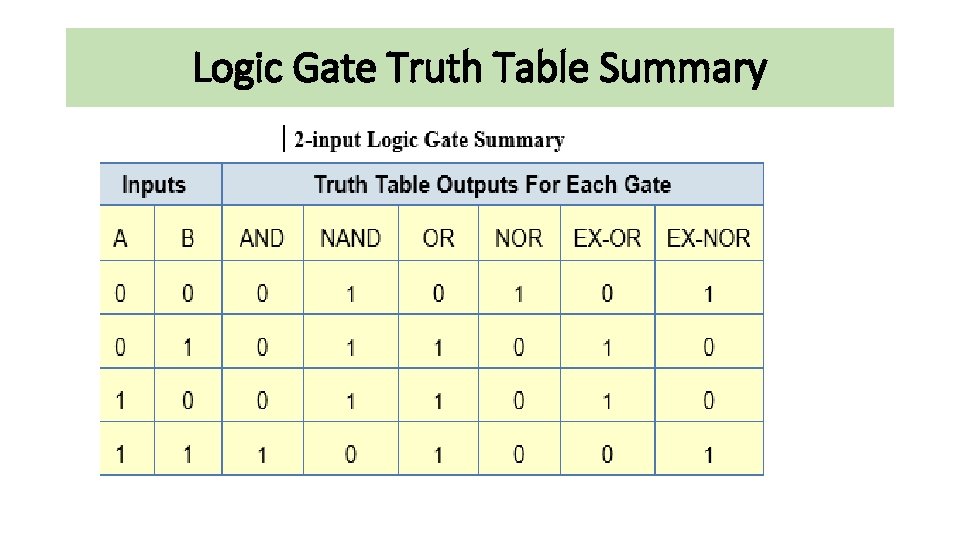
Logic Gate Truth Table • For example, consider a single 2 -input logic circuit with input variables labelled as A and B. • There are “four” possible input combinations or 22 of “OFF” and “ON” for the two inputs. • However, when dealing with Boolean expressions and especially logic gate truth tables, we do not general use “ON” or “OFF” but instead give them bit values which represent a logic level “ 1” or a logic level “ 0” respectively. • Then the four possible combinations of A and B for a 2 -input logic gate is given as: • • Input Combination 1. – “OFF” or ( 0, 0 ) Input Combination 2. – “OFF” – “ON” or ( 0, 1 ) Input Combination 3. – “ON” – “OFF” or ( 1, 0 ) Input Combination 4. – “ON” or ( 1, 1 )

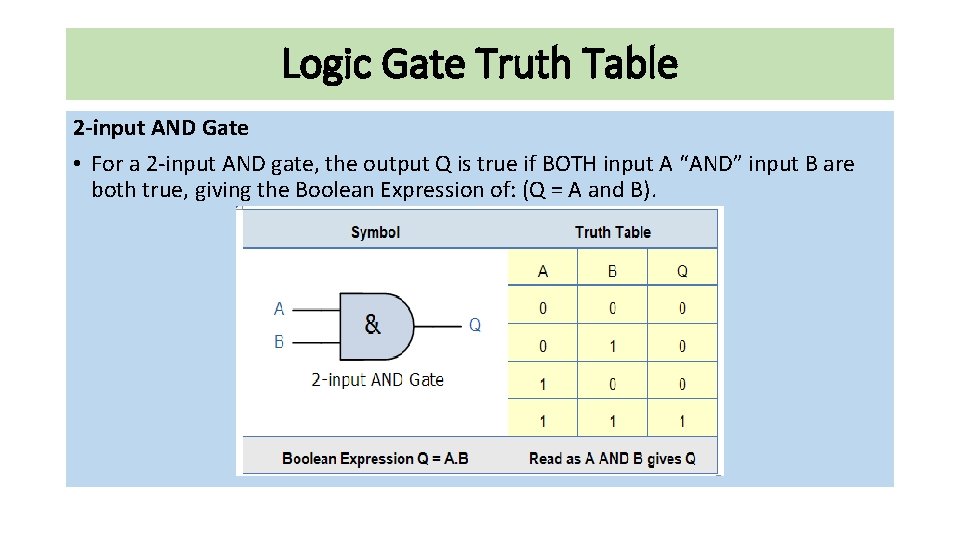
Logic Gate Truth Table 2 -input AND Gate • For a 2 -input AND gate, the output Q is true if BOTH input A “AND” input B are both true, giving the Boolean Expression of: (Q = A and B).

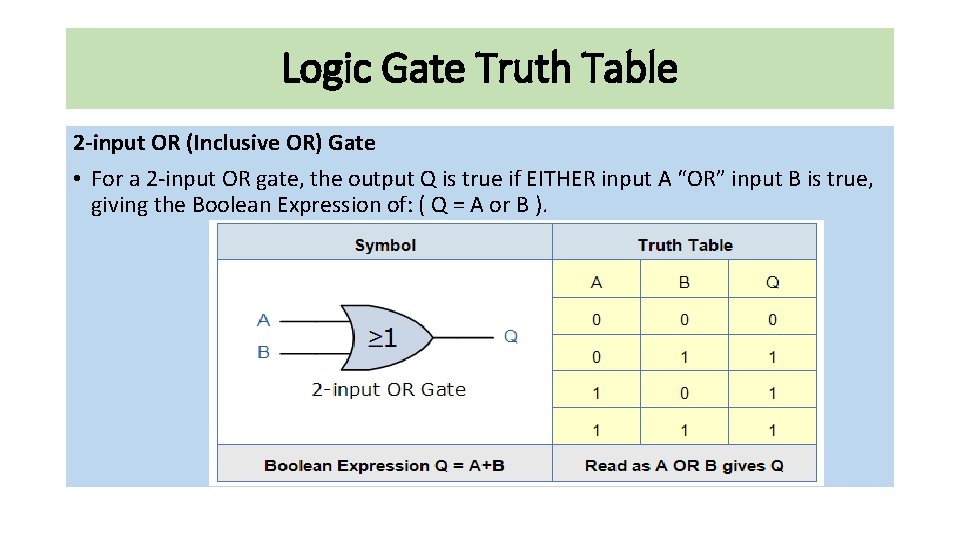
Logic Gate Truth Table 2 -input OR (Inclusive OR) Gate • For a 2 -input OR gate, the output Q is true if EITHER input A “OR” input B is true, giving the Boolean Expression of: ( Q = A or B ).

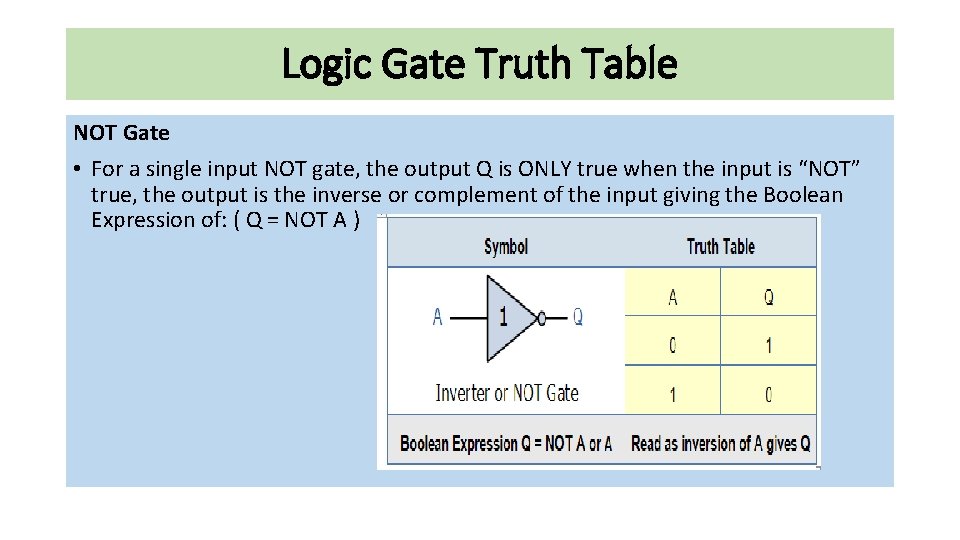
Logic Gate Truth Table NOT Gate • For a single input NOT gate, the output Q is ONLY true when the input is “NOT” true, the output is the inverse or complement of the input giving the Boolean Expression of: ( Q = NOT A )

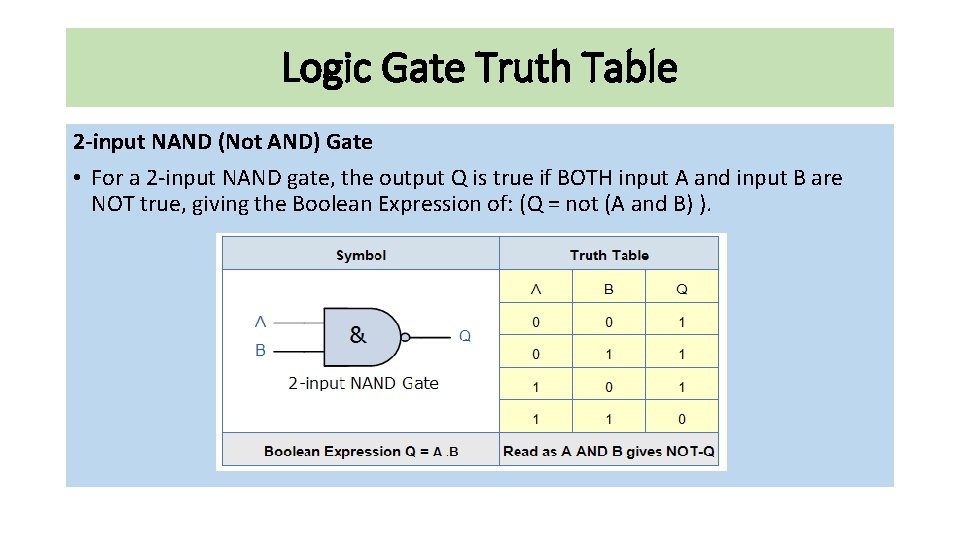
Logic Gate Truth Table 2 -input NAND (Not AND) Gate • For a 2 -input NAND gate, the output Q is true if BOTH input A and input B are NOT true, giving the Boolean Expression of: (Q = not (A and B) ).

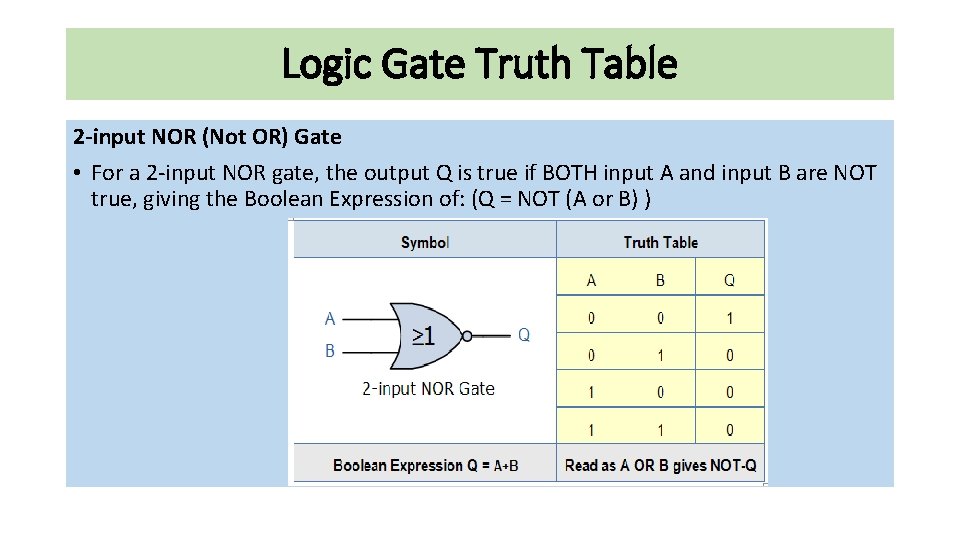
Logic Gate Truth Table 2 -input NOR (Not OR) Gate • For a 2 -input NOR gate, the output Q is true if BOTH input A and input B are NOT true, giving the Boolean Expression of: (Q = NOT (A or B) )

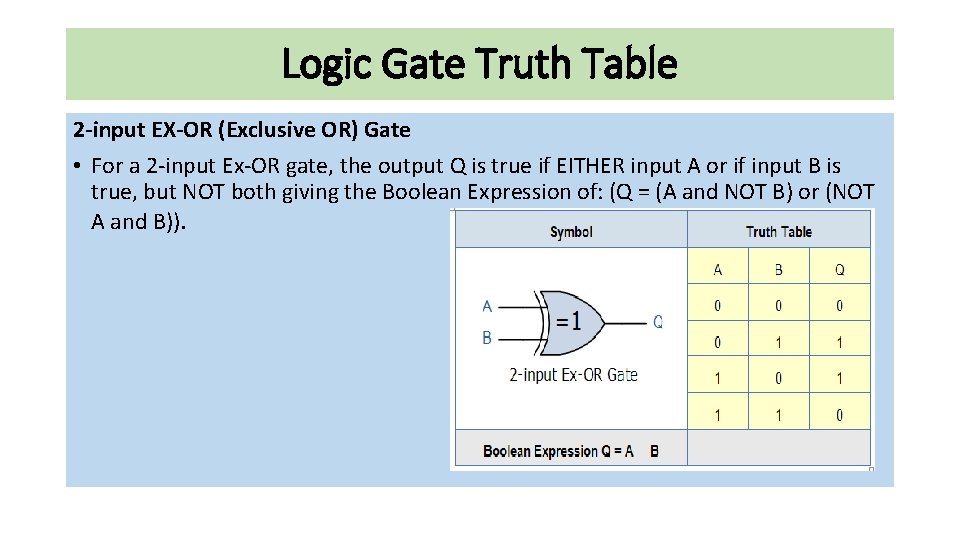
Logic Gate Truth Table 2 -input EX-OR (Exclusive OR) Gate • For a 2 -input Ex-OR gate, the output Q is true if EITHER input A or if input B is true, but NOT both giving the Boolean Expression of: (Q = (A and NOT B) or (NOT A and B)).

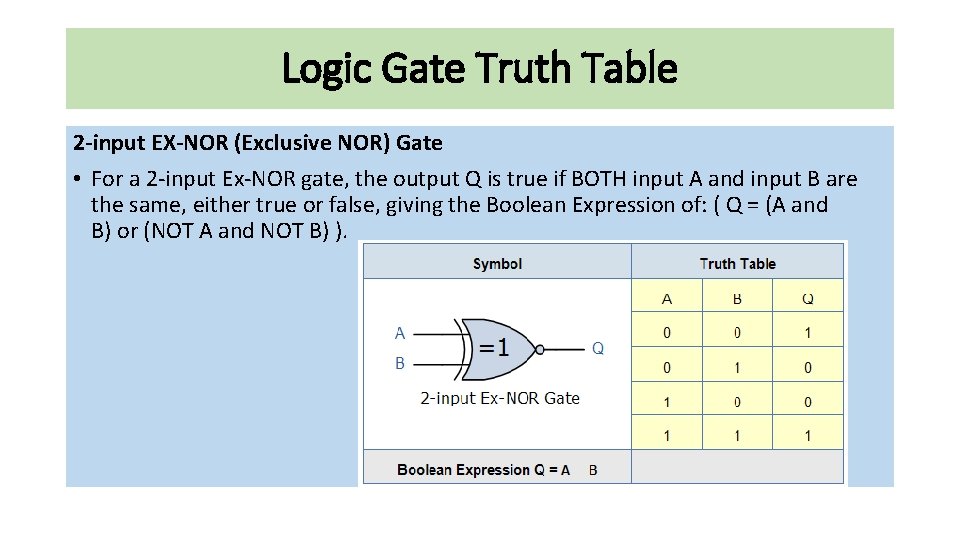
Logic Gate Truth Table 2 -input EX-NOR (Exclusive NOR) Gate • For a 2 -input Ex-NOR gate, the output Q is true if BOTH input A and input B are the same, either true or false, giving the Boolean Expression of: ( Q = (A and B) or (NOT A and NOT B) ).

Logic Gate Truth Table Summary

Questions 1. 2. 3. 4. 5. Explain the transformation process from data to knowledge What are the attributes of information quality? Discuss List the categories of systems with examples What is the difference between decimal system and binary system? Describe with proper diagrams different logic gates

Data, Information and System End of Chapter 1 Thank you