Maliyet Hacim Kr Analizleri 2 letme Genelinde MHK

Maliyet Hacim Kâr Analizleri 2

İşletme Genelinde MHK Analizleri Önceki MHK analizlerinden işletmenin tek tür mamul ürettiğini varsaymıştık. Bütün mamulleri bir arada ele almak suretiyle yürütülecek bu tür bir analizin tek tip üreten bir işletmeden ayrıldığı temel nokta, burada çeşitli mamullerin söz konusu olması nedeniyle, satış hacminin toplam satış miktarı ile ölçülememesi ve toplam net satışlardan hareket etme zorunluluğu ile karşılaşılmasıdır.

Örn: A, B ve C adlı üç tip mamul üzerinde çalışan X Sanayi İşletmesinin gelecek hesap dönemine ilişkin maliyet ve gelir tahminleri aşağıda gösterildiği gibidir. Syf 458

BBN = 200. 000 /%40 = 500. 000 TL’lik satış hacminde gerçekleşecektir. Bu analizi çeşitli soruları yanıtlayacak biçimde genişletmek olanaklıdır. Örn: İşletmenin gelecek hesap döneminde 200. 000 TL’lik bir kâr sağlayabilmesi için gerekli satış hacmini belirleyelim. Gerekli Satış Tutarı = ( 200. 000 + 200. 000 ) / %40 = 1. 000 TL

Örn: Önceki örneğimizde maliyetler ve satış tutarının aynı olduğu ancak mamul satış oranlarını %30, %40, %30 yerine %40, %20 ve %40 olduğunu varsayarsak yani A mamulünden 40. 000 birim, B mamulünden 20. 000 birim ve C mamulünden 40. 000 satılmış olsa bu durumda ilgili değerler şu şekilde olacaktır.

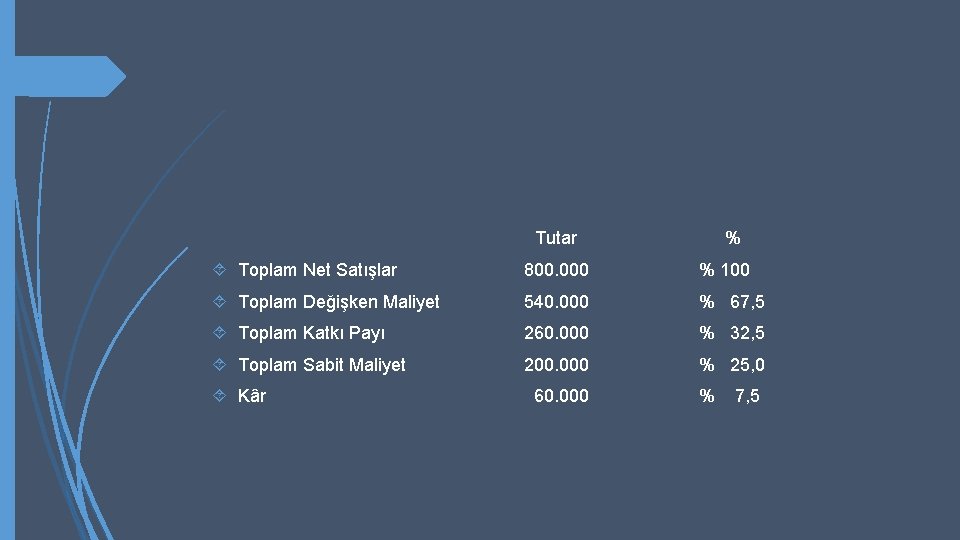
Tutar % Toplam Net Satışlar 800. 000 % 100 Toplam Değişken Maliyet 540. 000 % 67, 5 Toplam Katkı Payı 260. 000 % 32, 5 Toplam Sabit Maliyet 200. 000 % 25, 0 Kâr 60. 000 % 7, 5

Görülüyor ki, satış tutarı değişmediği halde, kâr ve kâr marjı yarıya inmiştir. BBN Satış Tutarı = 200. 000/ %32, 5 = 615. 384 TL 115. 384 TL’lik bir artış göstermiştir. Bu olumsuz değişmelerin nedeni, mamul karması içerisinde katkı oranı en yüksek olan B mamulünden diğer mamullere doğru bir kaymanın meydana gelmesidir.

Söz konusu üç mamulün katkı oranları hesaplarsak; A Mamulü Katkı Oranı = (10 – 6 ) / 10 = % 40 B Mamulü Katkı Oranı = ( 8 – 3 ) / 8 = % 62, 5 C Mamulü Katkı Oranı = ( 6 – 6 ) / 6 = % 0 Planlanan durumuna göre 40. 000 birim satılması umulan %62, 5 katkı oranına sahip B mamulünden ancak 20. 000 birim satılması; geri kalan 20. 000 birimin yarısının %40 katkı oranına sahip A mamulüne, diğer yarısının da katkı oranı %0 olan C mamulüne gitmesi nedeniyle meydana gelmiştir.

Mamul Bazında MHK Analizleri

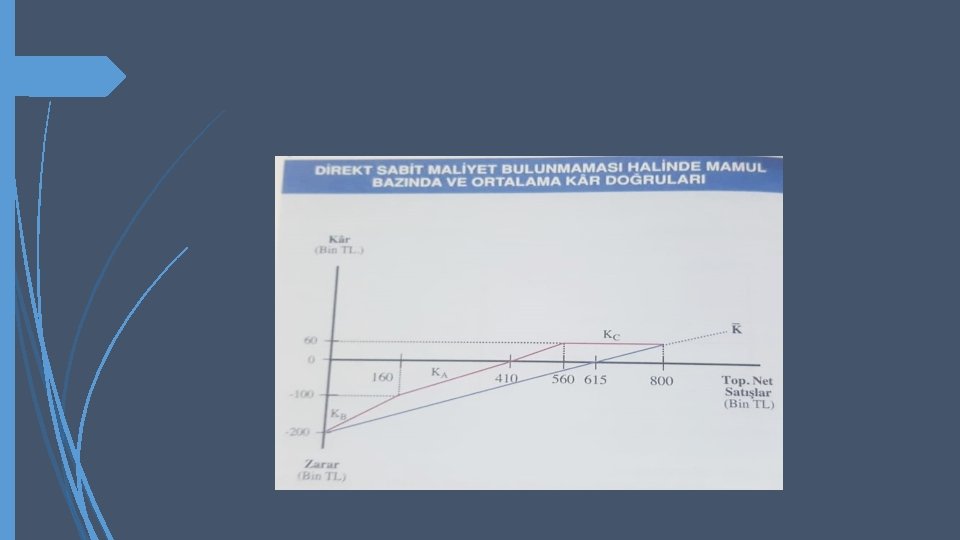
Tüm mamullerin bir arada gösterildiği dördüncü grafikte kâr doğrusu, katkı oranı en yüksek olan B mamulünden başlatılmıştır. B mamulünün direk sabit maliyeti (125. 000 TL) ile ortak sabit maliyetin (20. 000 TL) toplamı kadar (145. 000 TL) zarardan başlayan kâr doğrusu, B mamulünün satış hacmi olan 160. 000 TL de bu mamulün sağladığı 160. 000 x %62, 5 = 100. 000 TL’lik katkı sayesinde 45. 000 TL zarara inmektedir. Ancak, bu noktada A mamulünün devreye girmesi ve bu mamulün 40. 000 TL direkt sabit maliyetinin eklenmesi nedeniyle, zarar 85. 000 TL’ye yükseltmektedir.

A mamulünün 400. 000 TL olan fiili satış hacmine ulaşıldığında, işletmenin toplam satışları 400. 000 + 160. 000 = 560. 000 TL, kârı ise A mamulünün sağladığı 400. 000 x %40 = 160. 000 TL’lik katkı sayesinde -85. 00 + 160. 000 = 75. 000 TL olmaktadır. Buna C mamulünün kâr doğrusu da eklendiğinde, bir önceki kesimde son örnekte verilen 60. 000 TL’lik kâra ulaşılmaktadır.

En Uygun Mamul Karmasının Saptanması Çeşitli mamullerin kârlılık durumları konusundaki MHK analizlerinden elde edilecek bilgiler, üretim ve satış koşulları ile birlikte değerlendirilmek suretiyle, en uygun mamul karmasının saptanmasında kullanılabilir.

Örn: Yıllık toplam sabit maliyeti 150. 000 TL olan bir işletmede satış fiyatları sırasıyla 20 TL ve 10 TL birim değişken maliyetler ise 14 TL ve 6 Tl olan A ve B mamulü üretmektedir. İşletmenin Yıllık toplam makine kapasitesi 150. 000 saat olup, makinelerin hepsi hem A, hem de B mamulünün üretiminde kullanılabilmektedir. A mamulünün her birimi için 3 saatlik, B mamulünün için de 1 saatlik makine çalışmasına gerek vardır. Talep analizleri, şimdiki satış fiyatlarında A mamulünden yılda en çok 100. 000, B biriminden ise 75. 000 birim satılabileceğini ortaya koymuştur.

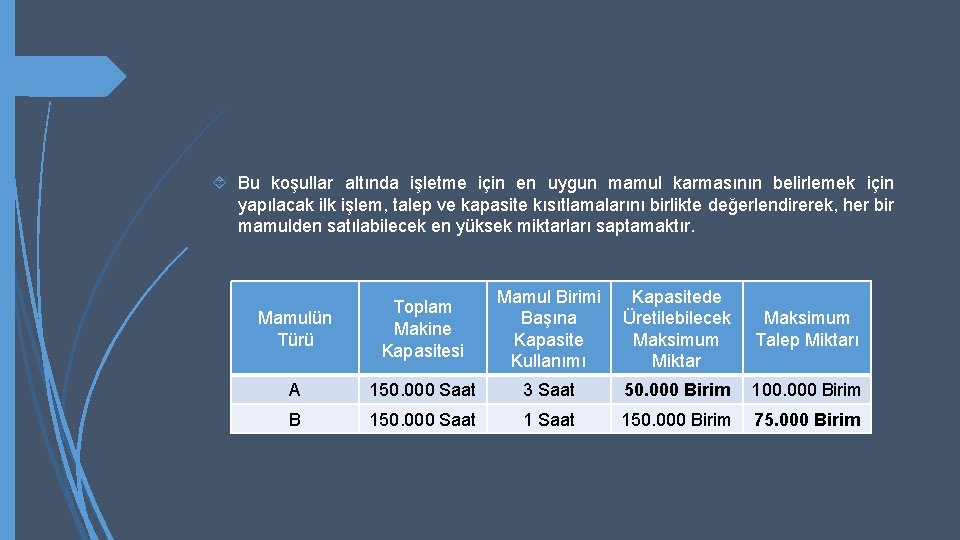
Bu koşullar altında işletme için en uygun mamul karmasının belirlemek için yapılacak ilk işlem, talep ve kapasite kısıtlamalarını birlikte değerlendirerek, her bir mamulden satılabilecek en yüksek miktarları saptamaktır. Mamulün Türü Toplam Makine Kapasitesi Mamul Birimi Başına Kapasite Kullanımı Kapasitede Üretilebilecek Maksimum Miktar Maksimum Talep Miktarı A 150. 000 Saat 3 Saat 50. 000 Birim 100. 000 Birim B 150. 000 Saat 150. 000 Birim 75. 000 Birim

Görüldüğü üzere, her ne kadar A mamulüne olan yıllık talep 100. 000 birim ise de, mevcut makinelerle bu mamulden en fazla 50. 000 birim üretilebilmektedir. Kapasitenin tümü A mamulüne yöneltilse bile satışları 50. 000 birim yukarı çıkma olasılığı yoktur. Bu yüzden 50. 000 birim kalın yazılmıştır. B mamulünden ise mevcut makinelerle yılda 150. 000 birim üretim yapma imkanımız vardır. Ama bütün makineler B mamulü üretirse, ürünlerin yarısı elimizde kalacaktır. Bu yüzden 75. 000 birim kalın yazılmıştır.

Maksimum satış miktarlarını esas alarak yalnız A ve yalnız B mamulünün üretilmesi durumunda sağlanacak kârlar; Kâr = Katkı Payı x Satış Miktarı – Sabit Maliyet Kâr ( A ) = ( 20 – 14 ) x 50. 000 – 150. 000 = 150. 000 Kâr ( B ) = ( 10 – 6 ) x 50. 000 – 150. 000 = 150. 000

Görülüyor ki, her iki mamulde aynı derecek kârlı bulunmaktadır. A mamulünden kullanılmaktadır. 50. 000 birim üretildiğinde mevcut kapasitenin tümü B mamulünden 75. 000 birim üretildiğinde ise yarısı kullanılmaktadır. Bu kalan boş kapasiteyi A mamulünün üretiminde kullanılırsa 75. 000 / 3 = 25. 000 birim üretilecektir. Bu da 150. 000 TL’lik ek kâr sağlayarak, toplam kâr 300. 000 TL olur. Bu durumda işletme öncelikle B mamulünü tercih edecek, geri kalan boş kapasiteyi ise A mamulüne yöneltecektir.

B Mam. Top. Katkı Payı ( 4 x 75. 000) 300. 000 A Mam. Top. Katkı Payı ( 6 x 25. 000) 150. 000 İşletmenin Top. Katkı Payı 450. 000 Toplam Sabit Maliyet 150. 000 Kâr 300. 000 İşletme için optimum mamul karması 75. 000 birim B mamulü ve 25. 000 birim A mamulüdür.

Doğrusal programlama tekniği: Mevcut kapasite (makine saati) ve talep kısıtları altında amaç, toplam katkı payının maksimizasyonu olacak şekilde model kurulabilir.

Eğrisel Fonksiyonlarda MHK Analizleri MHK analizlerinin dayandığı varsayımlardan iki tanesi de satış fiyatı ile birim değişken maliyette herhangi bir değişiklik olmaksızın işletmenin kapasiteye kadar satış yapabileceği idi.

Örn: x = satış miktarını göstermek üzere C işletmesinin toplam maliyet ve toplam gelir fonksiyonları aşağıdaki şekilde saptanmıştır. TG = -x² + 2. 000 x TM = x² + 320. 000

Başabaş Noktası Bu fonksiyonlardan hareket ederek; TG – TM = 0 (-x² + 2. 000 x) – (x² + 320. 000) = 0 -2 x² + 2. 000 x – 320. 000 = 0 Son denklem ax² - bx + c = 0 genel ikinci derece denkleminin özel bir şeklidir. Bu denklemin köklerini veren formül ise;

İkinci dereceden eğrisel fonksiyonların kullanılması halinde, başabaş noktası iki tane olmalıdır. Bunlardan küçük olanı (200 birim) kâra geçiş noktası, büyük olanı (800 birim) ise zarara geçiş noktasıdır.

Sağlanabilecek En Yüksek Kârı Veren Satış Hacmi Ekonomiye göre, bir işletme marjinal maliyetinin marjinal gelirine eşit olduğu üretim ve satış miktarında denge noktasına, yani en yüksek kâra ulaşır. Matematiksel yönden bakılırsa, marjinal maliyet, toplam maliyet eğrisinin eğimi, marjinal gelir ise toplam gelir eğrisinin eğimi olarak tanımlanabilir. Bu fonksiyonun eğimi ise türevi alınmak suretiyle bulunur. Toplam maliyet ve toplam gelir fonksiyonlarının türevlerini alıp birbirine eşitledikten sonra x’e göre çözersek, en yüksek kârı veren satış miktarını hesaplamış oluruz.

İşletme 500 birim üretip satmak suretiyle kârını maksimum kılacaktır.

En Yüksek Kârı Getiren Satış Fiyatı Maksimum kârı veren satış miktarı saptandıktan sonra sıra, bu miktarda satış yapabilmek için konulması gereken satış fiyatının belirlenmesine gelmektedir. Bu amaçla; Toplam Gelir = Satış Fiyatı x Satış Miktarı eşitliğinden satış fiyatını yalnız bırakırsak; Satış Fiyatı = Toplam Gelir / Satış Miktarı

500 birimlik satış sağlayan satış fiyatı şu halde işletmenin 5000 birimde elde edeceği toplam gelirin 500 birime bölümü kadar olacaktır. Toplam gelir fonksiyonunda ‘x’ e 500 değeri verilerek formül uygulanırsa; Satış Fiyatı = = -(500)² + 2. 000(500) 500 -250. 000 + 1. 000 500 = 1. 500 TL İşletme 1. 500 TL fiyat koyarsa 500 birimlik optimum satış hacmine erişecektir.

Sağlanabilecek En Yüksek Kâr Şimdi sağlanabilecek maksimum kâr miktarı kolaylıkla saptanabilir. Toplam Gelir = Toplam Maliyet = Maksimum Kâr = 500 birim x 1. 500 TL = 750. 000 TL (500)² + 320. 000 TL = 570. 000 TL 180. 000 TL

Kâr Fonksiyonundan hesaplarsak; K = TG – TM = (-2² + 2. 000 x) – (x² + 320. 000) K = -2 x² + 2. 000 x – 320. 000 Burada x’e 500 değeri verilir. K = (-2) (500)² + (2. 000) (500) – 320. 000 = -500. 000 + 1. 000 – 320. 000 = 180. 000 TL

Belirsizlik Halinde MHK Analizleri Önceki analizlerimizde gelecekteki koşulların genellikle tahmin edilebildiği varsayımından hareket etmiştik. Belirsizlik hali analize dahil edilmemişti. Belirsizlik halinin analizlerde göz önüne alınmaması bu analizlerden sağlanacak yararı büyük ölçüde azaltabilir.

Örnek üzerinden gidersek; Bir işletmede boş kapasite var olup, yönetim bu boşluğu doldurmak için yeni iki mamul üzerinde düşünmektedir. Her iki mamul de yıllık sabit maliyeti 400. 000 TL arttıracaktır. Her iki mamulün satış fiyatları ve birim değişken maliyetleri birbirine eşit olup, sırasıyla 10 TL ve 8 TL’dir. Her iki mamulde aynı miktarda kapasite kullanımı gerektirmektedir. Bu verilere göre her iki mamul için başabaş noktasının 200. 000 birim olduğunu hesaplayabiliriz.

MHK analizi geleneksel şekliyle bundan öte bilgi verememektedir. İki mamul arasında seçim yapabilmek için bu mamullerin beklenen satış hacimlerini bilmemiz gerekir. Diyelim ki, talep tahminleri A mamulünün yıllık satışlarının 300. 000, B mamulünün ise 350. 000 olacağını göstermektedir. Bu durumda işletme B mamulünü seçecektir.

Her iki mamulün beklenen yıllık satışlarının 300. 000 birim olduğunu düşünelim. Bu durumda işletme yönetimi A ve B mamulleri arasında kayıtsız mı kalacaktır? Bu iki mamule ait satış tahminleri belirsiz olduğu sürece, bu mamullere ilişkin göreceli risklerin analizde göz önünde tutulması, alınacak kararlar üzerinde olumlu etki yapacaktır. İşte bu kesimde MHK analizlerine istatistiksel olasılık kavramının uygulanması yoluyla bu analizlerin daha yararlı bir hale nasıl getirilebileceği incelenecektir.

Önceki verilen örnekte, alınacak karar üzerinde rol oynayan etkenler, satış fiyatı, birim değişken maliyet, toplam sabit maliyet ve her bir mamulün beklenen satış hacimleri idi. Karar almayı gerektiren bu tür problemlerde bu dört etkenin hepsi belirsiz olabilmektedir.

Ancak beklenen satış miktarına oranla satış fiyatları ve maliyetler oldukça belirli bulanabilir. Böyle bir durumda yönetici bu etkenleri kesin olarak alıp, analizlerini beklenen satışlar üzerinden yürütebilir ki, böyle bir tutum analizleri büyük ölçüde kolaylaştıracaktır. Biz de burada bu yolu izleyecek ve satış hacmi dışındaki etkenleri biliniyor kabul edeceğiz. Üzerinde duracağımız teknikler istenildiğinde diğer etkenlere de aynı şekilde uygulanabilir.

Önceki örneğimizde satış hacmi tesadüfi bir değişken olarak ele alınmıştır. İstatistikte tesadüfi değişken, miktarı bilinmeyen herhangi bir değişkendir. Örneğimizde diğer değişkenler (etkenler) bilindiğine göre, alınacak kararın doğruluğu tesadüfi değilken olan satış hacimlerine bağlıdır. Belirsizlik halini göz önünde bulunduran karar şekillerinden biri ise, tesadüfi değişkenin alabileceği çeşitli değerlere ilişkin olasılıkların tahminidir. Böyle bir tahmin sübjektif olasılık dağılımı adını alır. Bundan sonra yapılacak iş, en yüksek beklenen değere sahip alternatifin seçilmesidir.

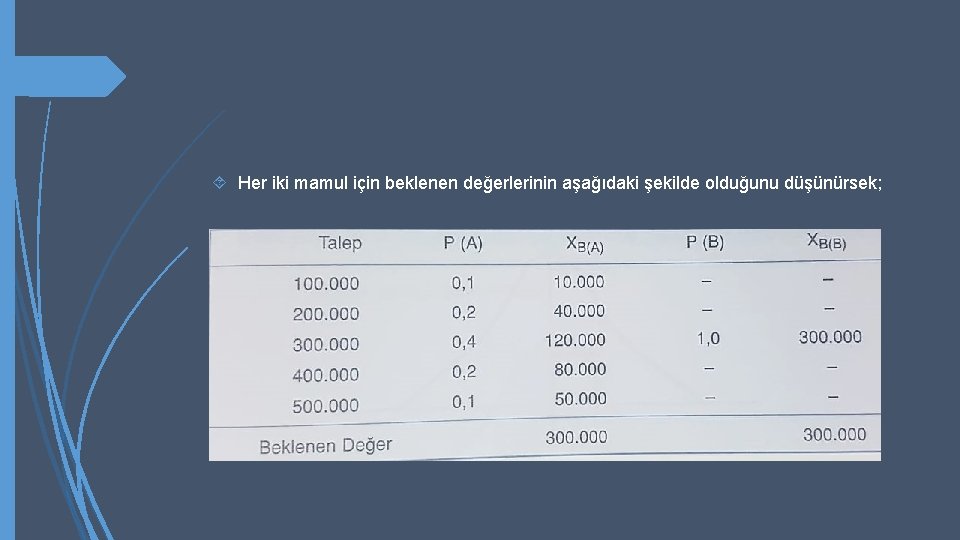
Tesadüfi değişkenin yani her mamule ilişkin satış hacimlerinin beklenen değeri, bu satış hacimlerinin hizalarındaki olasılıklarla çarpılması suretiyle bulunur. Diğer bir deyişle, beklenen değer ağırlıklı bir ortalamadır. A ve B mamullerinin beklenen değeri şu şekilde hesaplanabilir.

Beklenen değerden hareket edilirse, işletme yönetimi B mamulünü seçmelidir. A ve B mamullerinin beklenen kârları (Kb) ise aşağıdaki gibidir. A mamulü: Kb = 2 (300. 000) – 400. 000 = 200. 000 TL B mamulü: Kb = 2 (305. 000) – 400. 000 = 210. 000 TL

Her bir talep düzeyine tekabül eden olasılıklar, A ve B mamullerinin benzeri mamullere ait geçmişteki talep durumlarından yararlanılarak saptanabileceği gibi, geçişe ait talep verilerin mevcut olmaması halinde tamamen sübjektif olarak da belirlenebilir. Bu son durumda bile beklenen değer yaklaşımı yararlı sonuçlar verebilmektedir.

Her iki mamul için beklenen değerlerinin aşağıdaki şekilde olduğunu düşünürsek;

Tablodan görüldüğü gibi, her iki mamul için beklenen satış değerleri birbirine eşittir. Bu durumda beklenen değerden hareket etmek yanlış olur. A mamulü satışları 0, 1(%10) olasılıkla 100. 000 olabilmektedir. Ki bu durumda işletme 200. 000 ( 2 TL x 100. 000 – 400. 000) zarar edecektir. Öte yandan, bu mamul için satışların 300. 000 birimin üzerinde olması 0, 3 olasılığa sahiptir ve dolayısıyla A mamulünün B mamulünden daha fazla kâr getirme olanağı bulunmaktadır. Bu durumda alınacak karar, işletme yönetiminin tutucu (B mamulü) veya serüvenci ( A mamulü) oluşuna göre değişecektir.

Normal Dağılım Önceki kesimdeki tablolarda sıralanman talep düzeyleri, ortaya çıkması olası tüm talepleri yansıtmamaktadır. Örneğin 150. 000 veya 223. 500 birimlik talebin ortaya çıkma olanağı bulunmadığı varsayılmıştır. Bu nedenle ‘kesikli’ bir olasılık dağılımı yerine ‘sürekli’ bir dağılımın kullanılması daha gerçekçi olur. İstatistikte binom, poisson ve normal sürekli dağılımlar mevcuttur. Burada, hem en yaygın kullanılan dağılım olması, hem de hesaplama şekillerinin diğerlerine göre çok daha kolaylık sağlaması nedeniyle, normal dağılım esas alınacaktır.

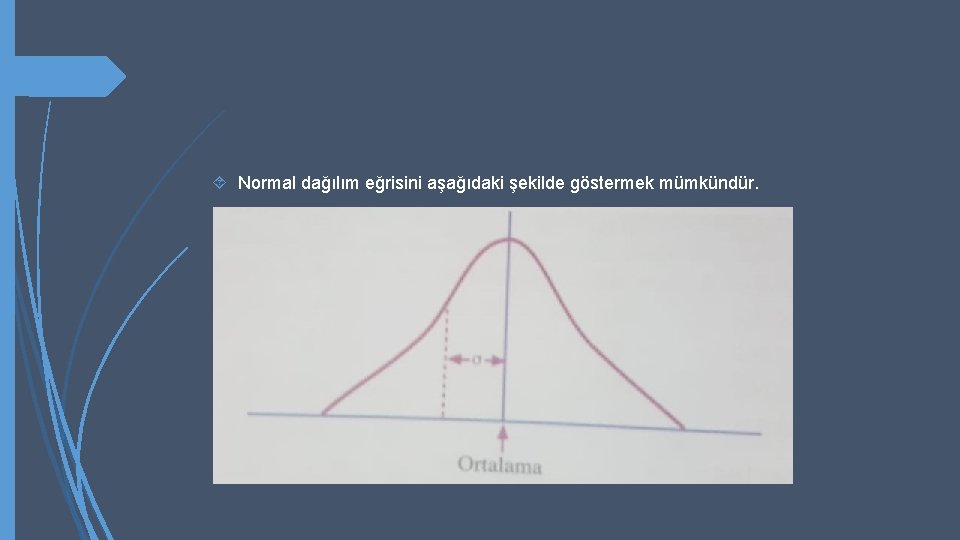
Normal dağılım; çan şeklinde simetrik ve sürekli bir eğri olup, bu eğrinin altında kalan 1’e eşittir. ( Önceki kesimde olasılıklar toplamının 1 olduğunu hatırlayalım. ) Bu eğri ortalamasında en yüksek değerine ulaşır ve altındaki alanın yarısı ortalamanın bir yanında, diğer yarısı da öteki yanında bulunur.

Normal dağılım eğrisini aşağıdaki şekilde göstermek mümkündür.

Yatay eksende tesadüfi değişkenin (beklenen satışlar) değerleri gösterilir. Herhangi normal olasılık dağılımı kolaylıkla saptanabilir. Bunun için ortalama ve standart sapmanın bilinmesi yeterlidir. Standart Sapma (σ), ortalama çevresindeki dağılımının ölçüsüdür. Her normal dağılım eğrisinin altındaki alan 1’e eşit olmakla birlikte, bir normal dağılım diğerinden daha geniş bir bölgeye yayılmış olabilir.

Örneğin, aşağıdaki iki normal dağılım altındaki alanlar ve ortalamalar birbirine eşittir.

Bu iki dağılımı birbirinden standart sapmalar ayırmaktadır. Standart sapma büyüdükçe, normal dağılım genişler. Şurası yanlış anlaşılmamalıdır ki, standart sapma bir alan değil, bir uzaklık ölçüsüdür. Kesikli yerine sürekli bir dağılım kullanıldığı zaman belirli bir değerin ortaya çıkma olasılığı grafitken okunamaz. Olasılıklar dağılım eğrisinin altında kalanla ifade edildiğinden, örneğin 100. 000 birimlik talep olasılığı değil de 99. 000 – 101. 000 arasında talep söz konusudur. Çünkü birinci halde alan mevcut değildir.

Şimdi şöyle bir örnek düşünelim: Bir işletmede pazarlama yönetici gelecek aydaki ortalama satışların 10. 000 birim olacağını tahmin etmektedir. İlgili dağıtım grafiği

Bu grafikten şu sonuçları çıkarabiliriz: 1 - Gerçek satışların 10. 000 – 11. 000 birim arasında bulunma olasılığı %20’dir. Bu ‘C’ alanında görülmektedir. Eğrinin simetrik olması nedeniyle satışların 9. 000 – 10. 000 birim arasında kalması olasılığı da %20’dir (B alanı). 2 - Gerçek satışların 11. 000’den fazla olması olasılığı %30’dur (D alanı). 3 - Satışların 9. 000 birimden fazla olması olasılığı %70’dir (B + C + D alanları).

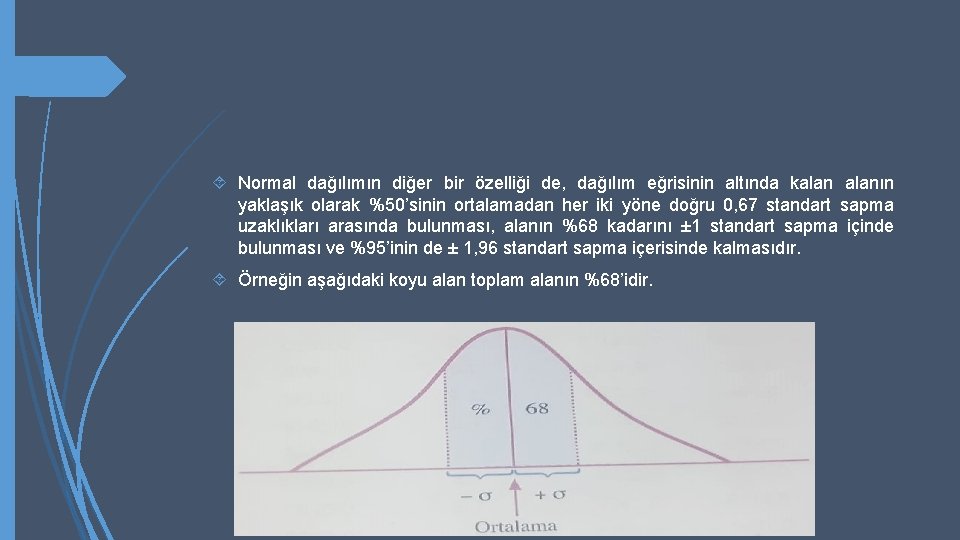
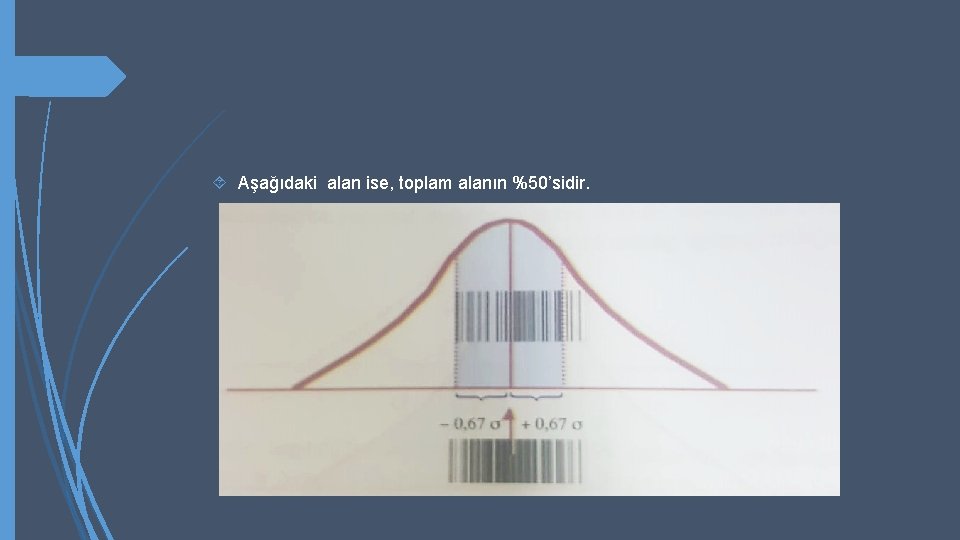
Normal dağılımın diğer bir özelliği de, dağılım eğrisinin altında kalanın yaklaşık olarak %50’sinin ortalamadan her iki yöne doğru 0, 67 standart sapma uzaklıkları arasında bulunması, alanın %68 kadarını ± 1 standart sapma içinde bulunması ve %95’inin de ± 1, 96 standart sapma içerisinde kalmasıdır. Örneğin aşağıdaki koyu alan toplam alanın %68’idir.

Aşağıdaki alan ise, toplam alanın %50’sidir.

Normal dağılım olasılıkları, bu amaçla düzenlenmiş bir tablodan öğrenilebilir. Böyle bir tablo aşağıda verilmiştir. Bu tablo, normal dağılım grafiğinde ortalamanın sağ yanını temsil etmektedir. Tablo, tesadüfi (rassal) değişkenin ‘Ortalama + Z standart sapma’ değerlerinden daha büyük değerler alma olasılığını ortaya koymaktadır.

Örneğin tesadüfi değişkenin ‘ortalama + 0, 35 standart sapma’ değerinden daha fazla bir değer alması olasılığı 0, 3632 (%36, 32) dir. Yine tesadüfi değişkenin ortalamadan bir standart sapma fazla olan değerden daha yüksek bir değer alması olasılığı 0, 1587 (%15, 87) dir.

Daha önce verdiğimiz örneği tablodan yararlanarak tekrar incelersek; dağılım ortalaması 10. 000 birim, satışların 11. 000 birimden fazla olması olasılığı (D alanı) %30 idi. Son tabloyu incelersek, bir tesadüfi değişkenin ortalama + 0, 5 standart sapmadan daha fazla bir değere sahip olması olasılığının 0, 3085 olduğunu görürüz. Dolayısıyla 11. 000 – 10. 000 birim yaklaşık olarak 0, 5 standart sapmaya karşılık demektir. Buradan 1 standart sapma = 2. 000 birim sonucunu çıkartabiliriz.

Standart sapmanın 2. 000 olduğu bilinince, buradan hareketle D alanını [P (satışlar > 11. 000)] hesaplayabiliriz. Tablo bize ortalama artı Z standart sapmadan daha büyük değerlerin olasılığını verdiğine göre Z’yi şu şekilde hesaplayabiliriz. Z = (Gerçek Satışlar – Ortalama Satışlar) / Standart Sapma Z = (11. 000 – 10. 000) / 2. 000 = 0, 5 Standart sapma

Satışların 11. 000’den fazla olması olasılığı ise tabloda 0, 5 standart sapmaya tekabül eden 0, 3085 veya yuvarlak olarak %30’dur ki bu D alanıdır. Normal dağılım eğrisi simetrik olduğundan, yukarıdaki tabloyu ortalamanın sol yanı içinde kullanmak olanaklıdır.

Örneğin, satışların 9. 000 birimden fazla olması olasılığı şu şekilde bulanabilir; Satışların 9. 000 birimden az olması olasılığı 11. 000 fazla olması olasılığı ile aynı olduğundan, 0, 30’dur (tabloda 0, 3085). Eğrinin altındaki alan 1’e eşit olduğundan; P (Satışlar > 9. 000) = 1 – P (Satışlar < 9. 000) P (Satışlar > 9. 000) = 1 – 0, 30 = 0, 70 Satışların 9. 000 – 10. 000 arasında olması olasılığı ise; P (9. 000 < Satışlar < 10. 000) = 1 – P (Satışlar > 10. 000) – P (Satışlar < 9. 000) = 1 – 0, 50 – 0, 30 = 0, 20

Normal Dağılım ve MHK Analizleri Analizde satış hacmi bir tesadüfi değişken olarak alınmıştır. Diyelim ki, analizin yapıldığı işletme tek bir mamul üretmek ve adedini 3. 000 TL’ye satmaktadır. Toplam sabit maliyet yılda 5. 800. 000 TL, birim başına değişken maliyet ise 1. 750 TL’dir. Bu durumda başabaş noktası; Xbb = 5. 800. 000 / (3. 000 – 1. 750) = 4. 640 birim olacaktır.

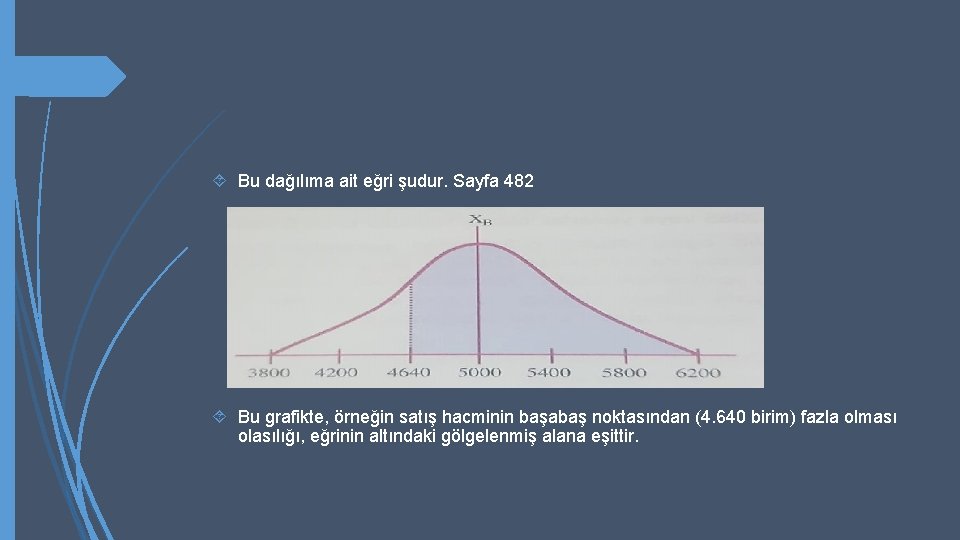
Şimdi satış yöneticisinin beklenen ortalama satış hacminin 5. 000 birim olacağını ve gerçek satışların bu miktarın altında veya üzerinde olma şansının eşit bulunduğunu tahmin ettiğini düşünelim. Satış yöneticisi aynı zamanda, gerçek satışların 2/3 (%67) olasılıkla beklenen ortalama etrafında her iki yönde 400’er birimlik bir değişim aralığı içerisinde bulunacağını düşünmektedir. Bu sübjektif tahminler normal bir olasılık dağılımı şekline dönüştürülebilir. Bu normal dağılım ortalaması Xb = 5. 000 birim, standart sapması ise: σ = 400 birimdir.

Bu dağılıma ait eğri şudur. Sayfa 482 Bu grafikte, örneğin satış hacminin başabaş noktasından (4. 640 birim) fazla olması olasılığı, eğrinin altındaki gölgelenmiş alana eşittir.

Satış fiyatı, birim başına değişken maliyet ve toplam sabit maliyetin kesinlikle bilindiği varsayılırsa, beklenen kâr şu şekilde bulunur.

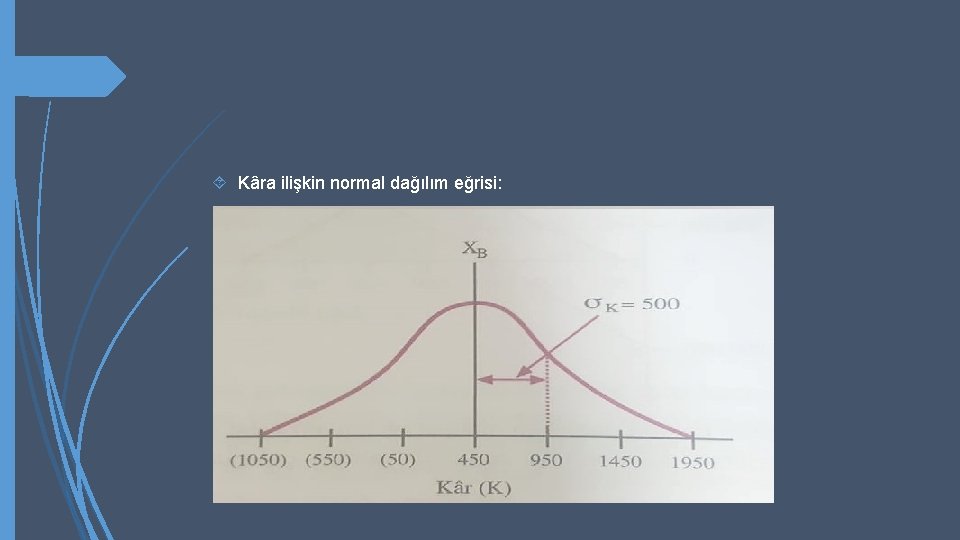
Beklenen ortalama kâr 450. 000 TL olarak hesaplanmıştı. Önceki eğrinin satışlara ait standart sapması σx = 400 birimdi. Bu sapmayı katkı payı ile çarparak kâra ilişkin standart sapmayı buluruz. σk = (σx) x KP σk = 400 x 1. 250 = 500. 000 TL

Kâra ilişkin normal dağılım eğrisi:

Önceki olasılık dağılıma göre ve daha önce verdiğimiz ‘Normal Dağılım Eğrisi Altında Kalan Alan’ tablosunu kullanarak şu olasılıkları hesaplayabiliriz. 1 - Zarar etmeme olasılığı: Bu kârların sıfırdan büyük olması olasılığıdır ve sıfır kâr noktasının sağ tarafındaki alana eşittir. Eğrinin tümünün altındaki alan 1 olduğundan, zarar etmeme olasılığı P (K > 0) = 1 – zarar etme olasılığı [P (K < 0)] şeklinde hesaplanabilir. Dağılım simetrik olduğundan, tablo ortalamanın sol yanı içinde kullanılabilir.

Hangi noktada zararların başladığını standart sapma türünden şu şekilde hesaplarız. Z = (Ortalama Kâr – Gerçek Kâr) / Standart Sapma Z = (450 – 0 ) / 500 = 0, 9 Yorumlarsak, ortalamanın 0, 9 standart sapma kadar solundan itibaren işletme zarar etmeye başlamakta ve daha sola gidildikçe zararlar artmaktadır. P (K < Ortalamadan 0, 9 standart sapma) = 0, 184 Dolayısıyla; P ( K >0 ) 1 – 0, 184 = 0, 816

2 - 200. 000 TL’den fazla bir kâr sağlama olasılığı yine aynı şekilde hesaplanır. P(K > 200) = 1 – P ( K < ( 450 – 200 ) / 500 σ = 1 – P (K < Ortalamadan 0, 5σ) = 1 – 0, 3085 = 0, 692

3 - 300. 000 TL’den fazla bir zarara uğrama olasılığı; P ( Z > 300) = P(K < 450 – (300) / 500 σ = P (Z > Ortalamadan 1, 5 σ) = 0, 067

Yönetici, başabaş satış hacminin 4. 640 birim, beklenen satışların 5. 000 birim ve beklenen kârın 450. 000 TL olduğunu bilmekle birlikte, özet olarak verilen şu bilgiler de karar almasına yardımcı olacaktır. 1 - Başabaş noktasına ulaşabilme olasılığı %81, 6’dır 2 - En azından 200. 000 TL kâr sağlama olasılığı %69, 2’dir 3 - En azından 450. 000 TL kâr sağlama olasılığı %50’dir 4 - Başabaş noktasına ulaşamama olasılığı %18, 4’dür. 5 - 300. 000 TL veya daha fazla bir zarara uğrama olasılığı %18, 4’dür.