Making a Scientific Graph The Basics Identifying Variables

Making a Scientific Graph The Basics.

Identifying Variables • Independent Variable (manipulated variable) – the thing the scientist is changing – gets plotted along the x axis – A control group is usually tested which gets none of the independent variable • Dependent Variable (responding variable) – the thing responding to the change – gets plotted on the y axis • Example: – Adding Miracle*Gro to help tomato plants grow

Independent & Dependent Variables • Your Turn • Joe wants to see if adding sugar to water will affect the density of the water. He designs an experiment where he measures the density of pure water, then dissolves 5 grams of sugar in and measures the density again. Next, 5 more grams of sugar are added and the density is determined yet again. This is repeated until no more sugar dissolves. • Identify the independent and dependent variable in Joe’s experiment.

Components of a Graph • Axis Labels – Each variable should be clearly labeled with the type of measurement (Mass, Volume, Length, etc) – The units used are put in parenthesis

Components of a Graph • Title –Minimum title: Y vs X • Examples –mass vs volume –Must always include both variables –Better titles are a little more descriptive • The effect of (ind variable) on (dep variable) of (object) • Examples –The effect of percentage sugar on density of water –The effect of Mass of Miracle*Gro on the height of tomato plants –“Effect” is the noun, “Affect” is the verb

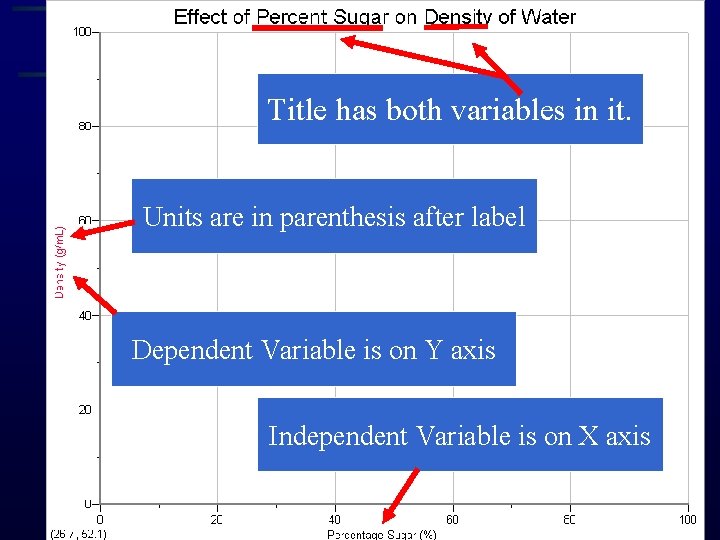
Components of a Graph • Axis Labels Title has both variables in it. – Show example graphs here • Units are in parenthesis after label Dependent Variable is on Y axis Independent Variable is on X axis

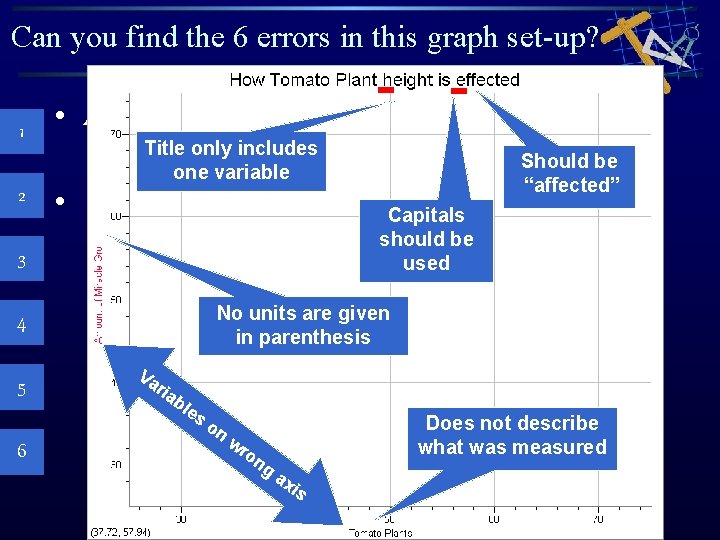
Can you find the 6 errors in this graph set-up? 1 2 • Axis Labels • Title only includes – Show example graphs here one variable Capitals should be used 3 No units are given in parenthesis 4 5 Va ria bl e s 6 Should be “affected” on wr on g Does not describe what was measured ax is

Your Turn • Use your graph paper to include a proper title and axis labels for this experiment.

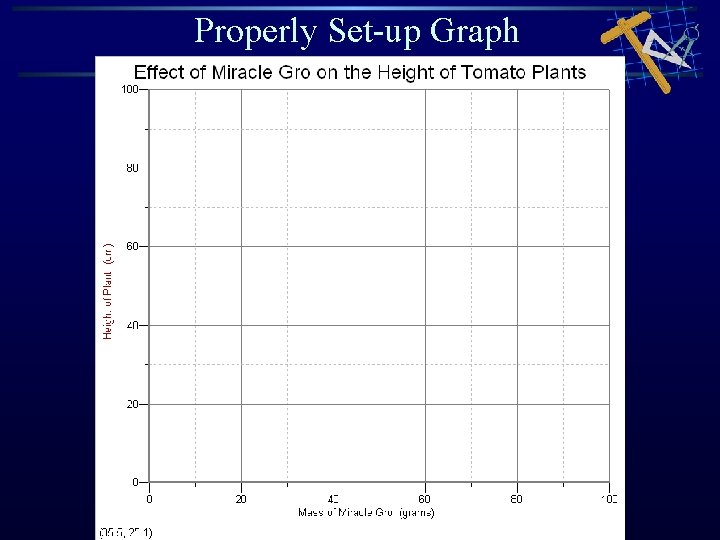
Properly Set-up Graph

Components of a Graph • Scale – In a Scientific Graph, the scale is zoomed in so that the graph “fills the paper” – to set scale, look at the range of your data for each variable – Put lowest value near bottom edge of graph and highest value near top – This span should cover at least 75% of graph – Scale does not have to start at 0, 0 – Try to make every block equal to a “nice” number • 1, 2, 4, 5 or any division of 10 of these (0. 2, . 05, 400. etc) – Stay away from ‘ugly’ scales • Every block = 3, 7, 9, etc

Identifying Variables - Example Let’s say we were making a graph of the relationship the between the temperature and the volume of a balloon. If we did this by changing the temperature and recording what the consequent volume was, then the _____ would be the independent variable, and the ______ would be the dependent variable.

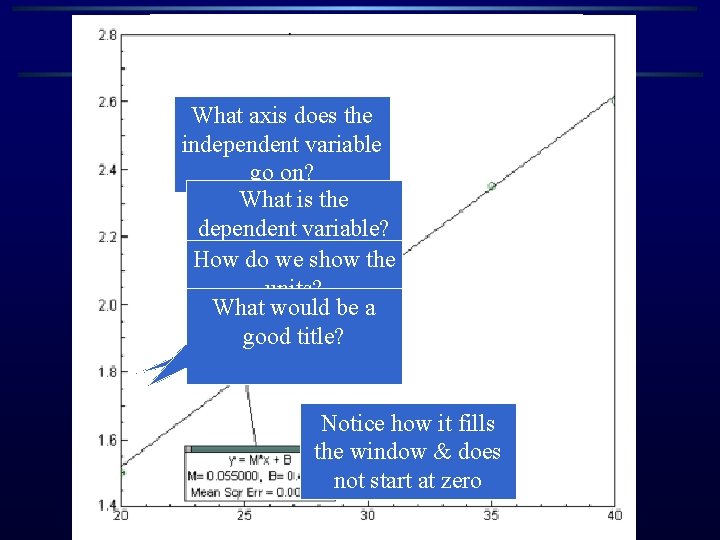
What axis does the independent variable go on? What is the dependent variable? How do we show the units? What would be a good title? Notice how it fills the window & does not start at zero

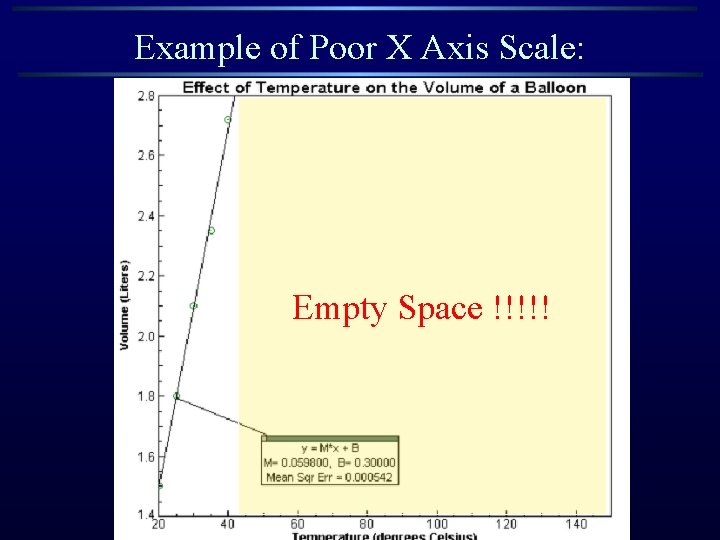
Example of Poor X Axis Scale: Empty Space !!!!!

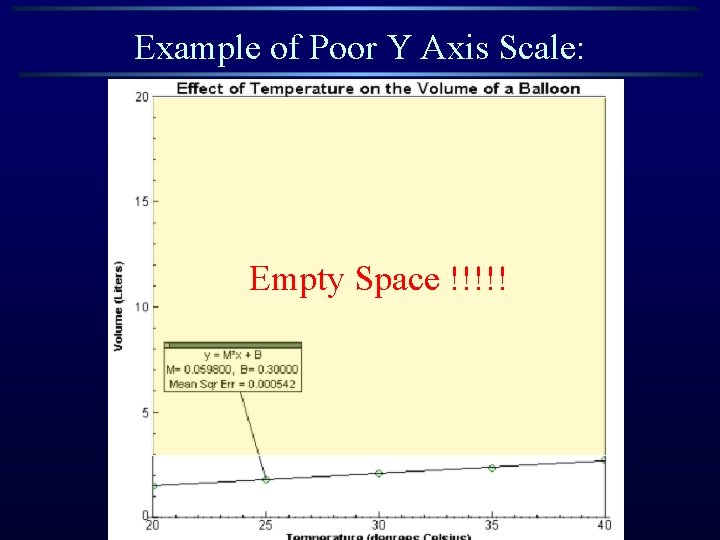
Example of Poor Y Axis Scale: Empty Space !!!!!

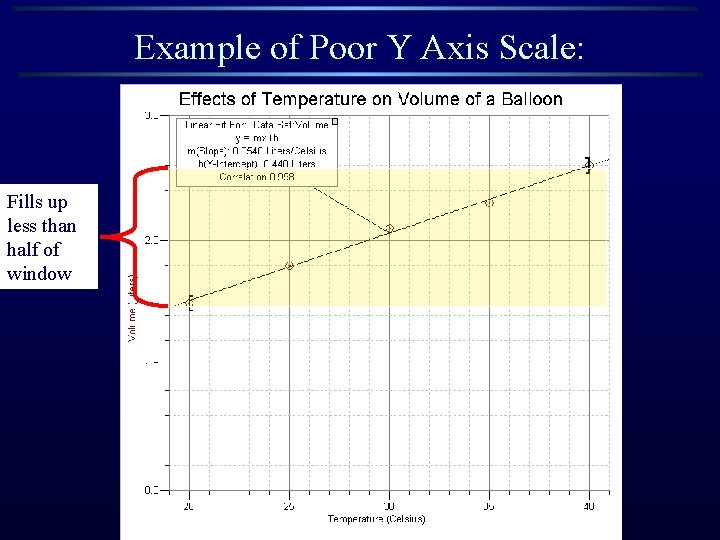
Example of Poor Y Axis Scale: Fills up less than half of window

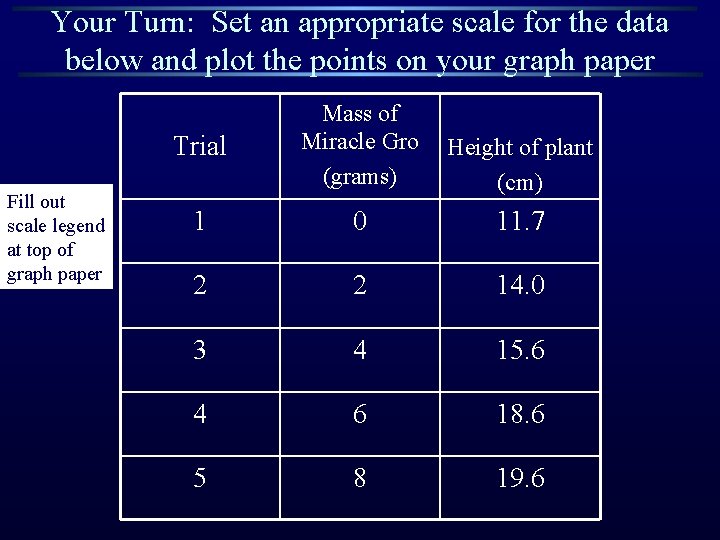
Your Turn: Set an appropriate scale for the data below and plot the points on your graph paper Fill out scale legend at top of graph paper Trial Mass of Miracle Gro (grams) Height of plant (cm) 1 0 11. 7 2 2 14. 0 3 4 15. 6 4 6 18. 6 5 8 19. 6

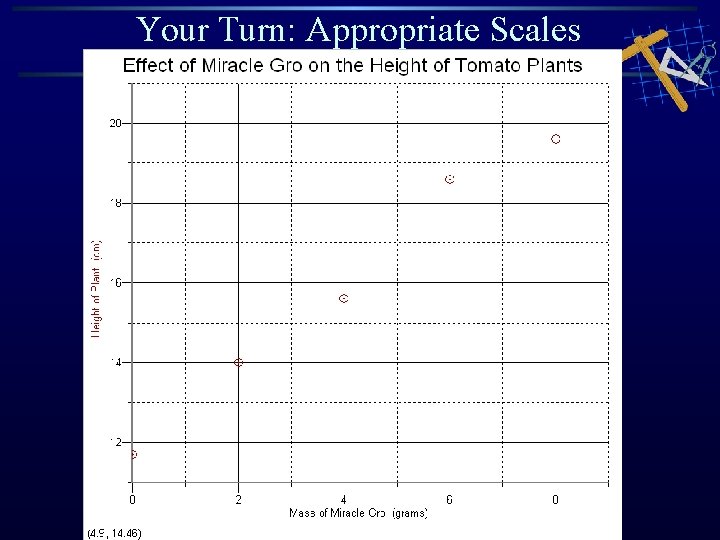
Your Turn: Appropriate Scales

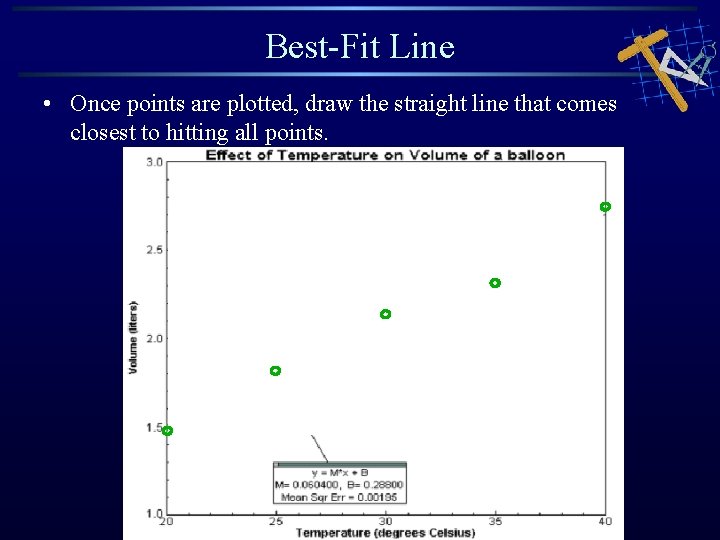
Best-Fit Line • Once points are plotted, draw the straight line that comes closest to hitting all points.

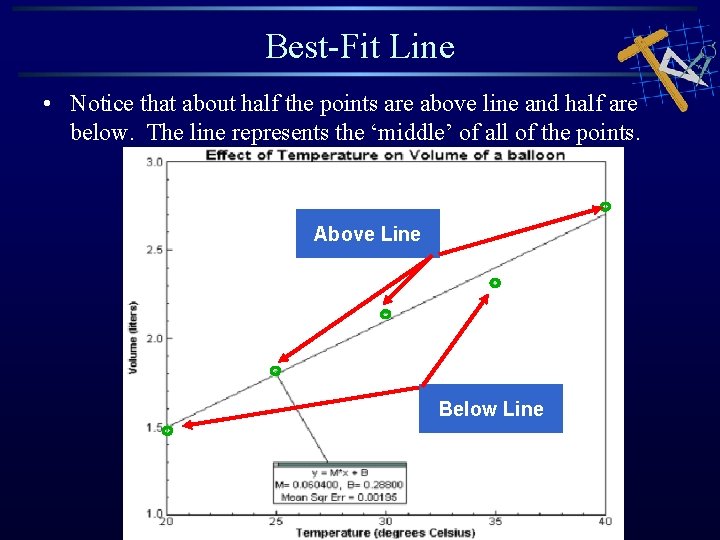
Best-Fit Line • Notice that about half the points are above line and half are below. The line represents the ‘middle’ of all of the points. Above Line Below Line

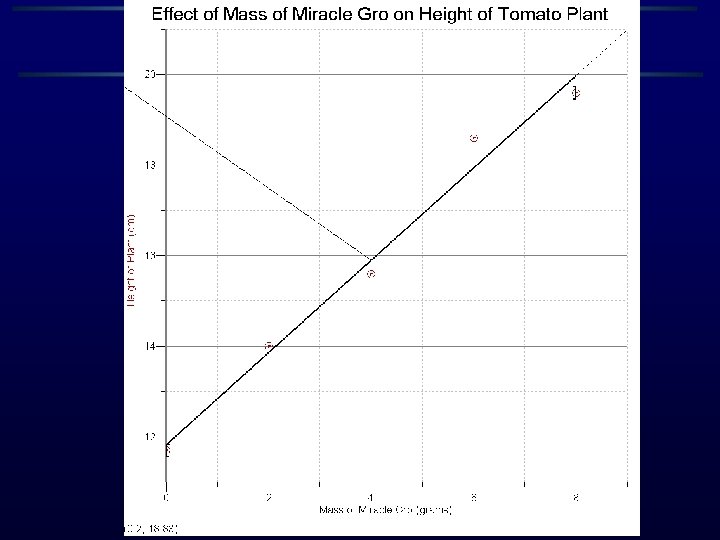
Your Turn • Draw the best-fit line on your Miracle Gro Graph • Rulers are in the side drawers

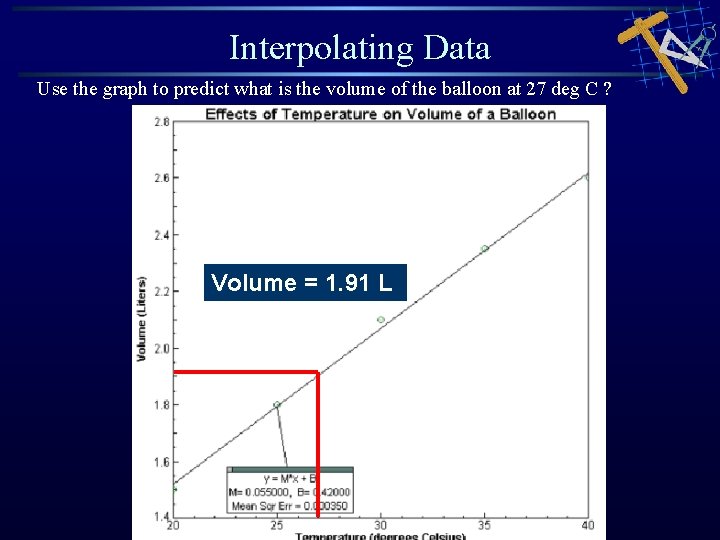
Interpolating Data Use the graph to predict what is the volume of the balloon at 27 deg C ? Volume = 1. 91 L

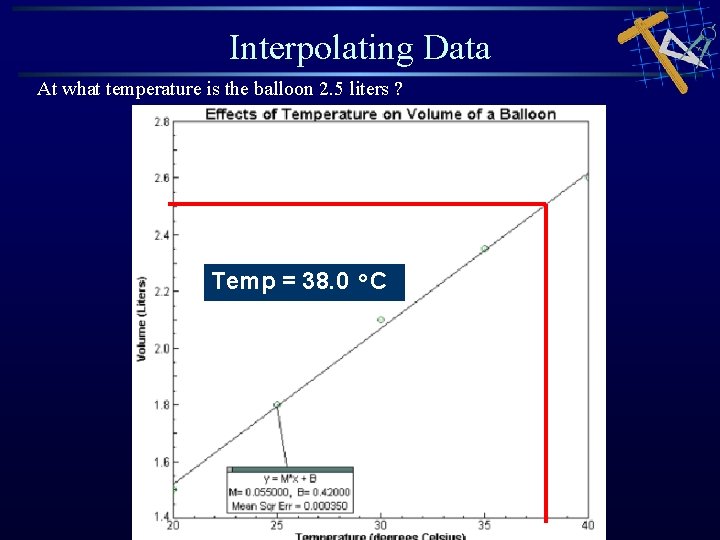
Interpolating Data At what temperature is the balloon 2. 5 liters ? Temp = 38. 0 °C

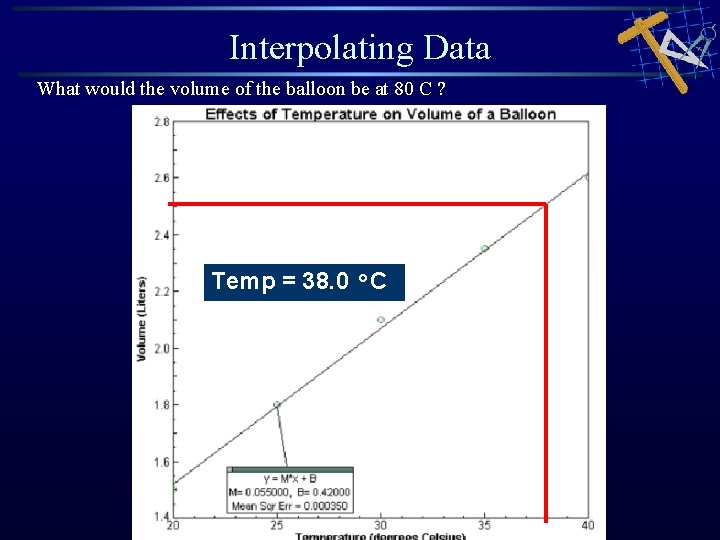
Interpolating Data What would the volume of the balloon be at 80 C ? Temp = 38. 0 °C

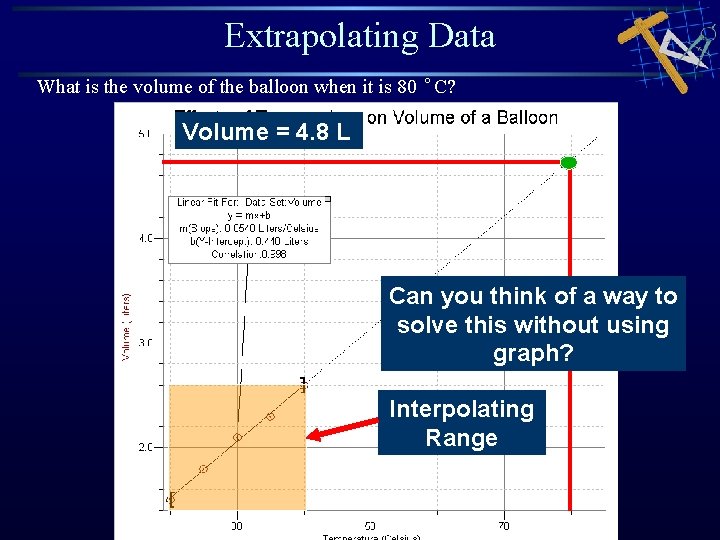
Extrapolating Data What is the volume of the balloon when it is 80 °C? Volume = 4. 8 L Can you think of a way to solve this without using graph? Interpolating Range

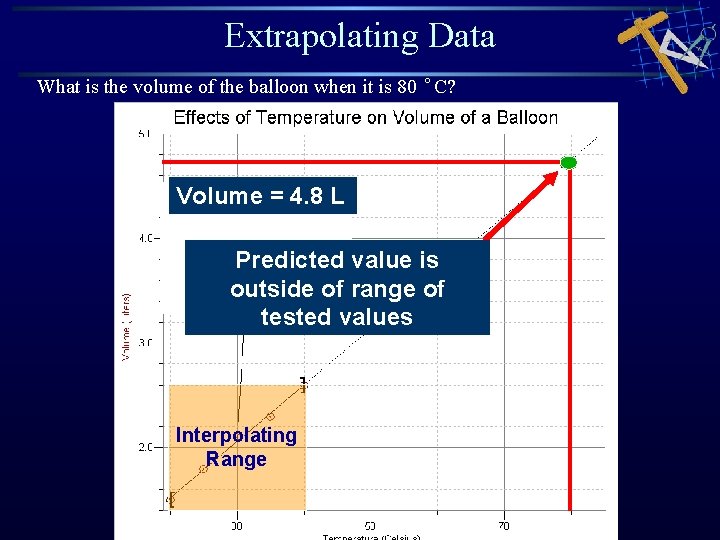
Extrapolating Data What is the volume of the balloon when it is 80 °C? Volume = 4. 8 L Predicted value is outside of range of tested values Interpolating Range

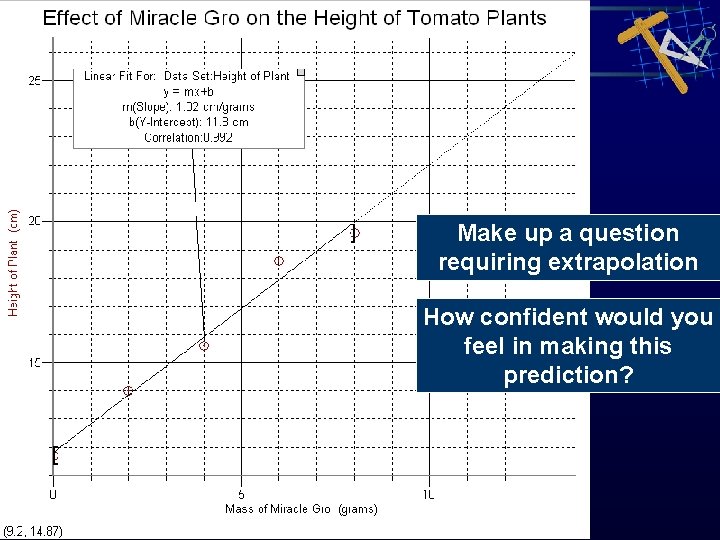
Make up a question requiring extrapolation How confident would you feel in making this prediction?

• Explain the difference between interpolating and extrapolating from your data. Compare the reliability of the two.

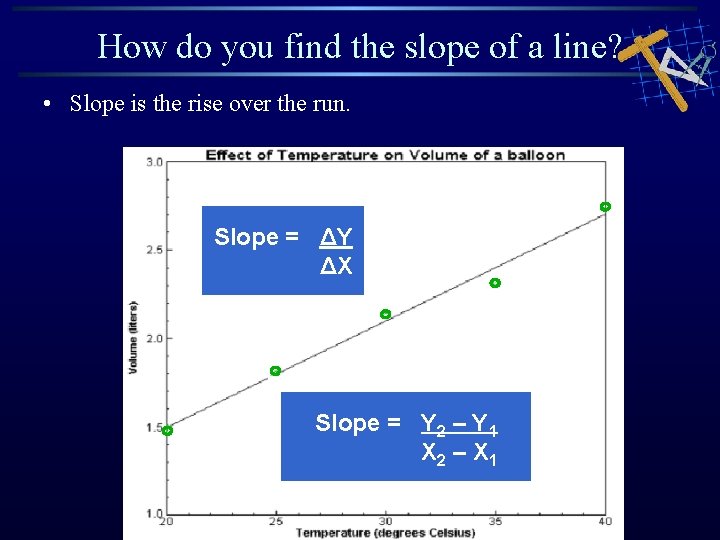
How do you find the slope of a line? • Slope is the rise over the run. Slope = ΔY ΔX Slope = Y 2 – Y 1 X 2 – X 1

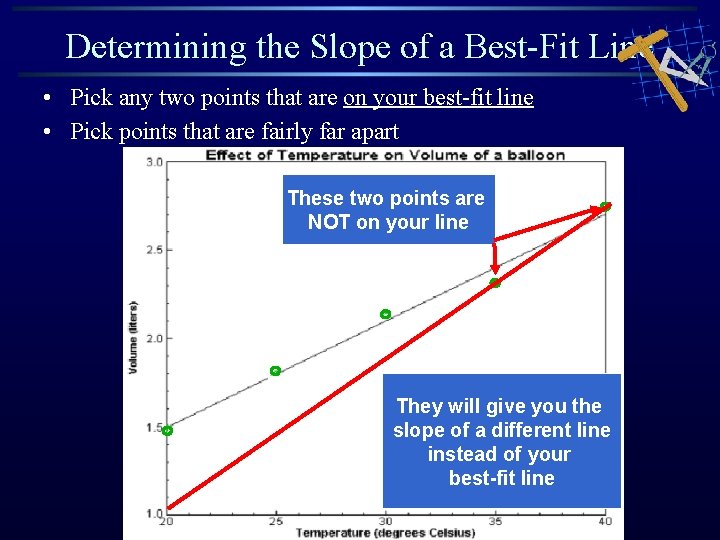
Determining the Slope of a Best-Fit Line • Pick any two points that are on your best-fit line • Pick points that are fairly far apart These two points are NOT on your line They will give you the slope of a different line instead of your best-fit line

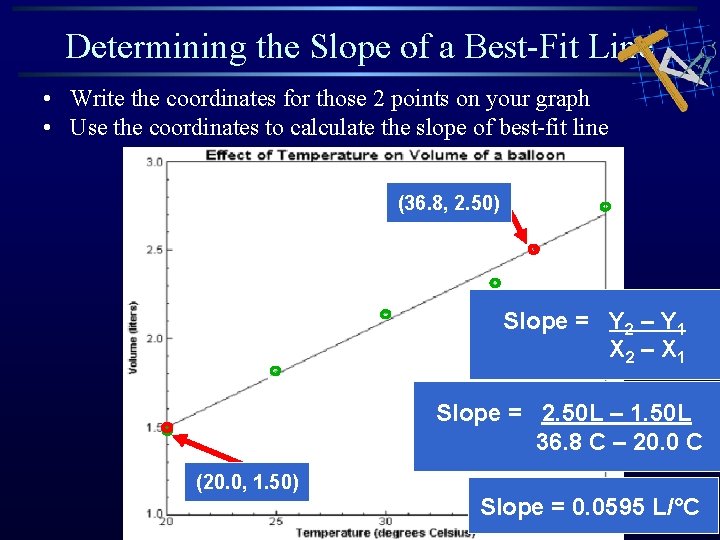
Determining the Slope of a Best-Fit Line • Write the coordinates for those 2 points on your graph • Use the coordinates to calculate the slope of best-fit line (36. 8, 2. 50) Slope = Y 2 – Y 1 X 2 – X 1 Slope = 2. 50 L – 1. 50 L 36. 8 C – 20. 0 C (20. 0, 1. 50) Slope = 0. 0595 L/°C

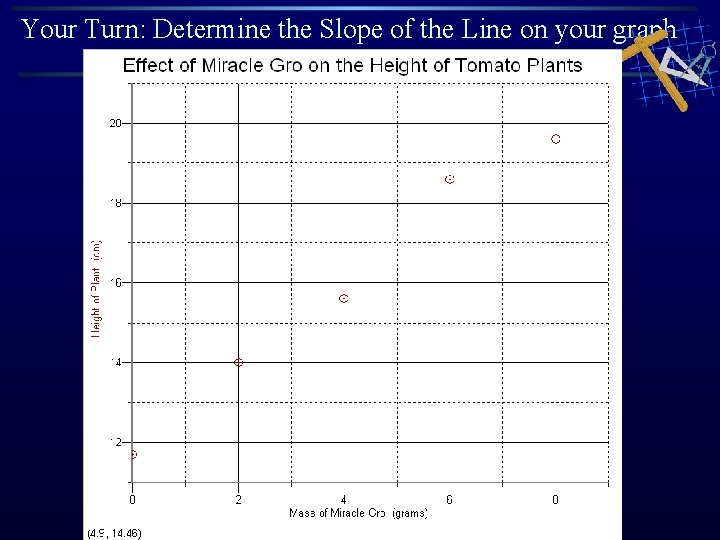
Your Turn: Determine the Slope of the Line on your graph

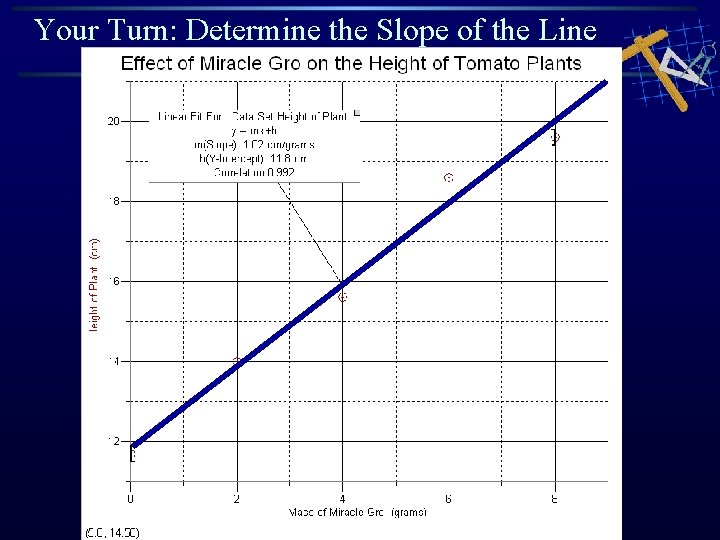
Your Turn: Determine the Slope of the Line

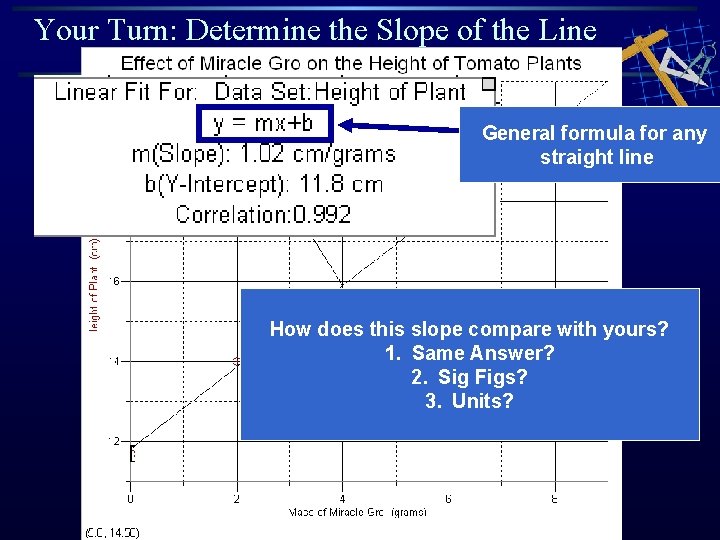
Your Turn: Determine the Slope of the Line General formula for any straight line How does this slope compare with yours? 1. Same Answer? 2. Sig Figs? 3. Units?

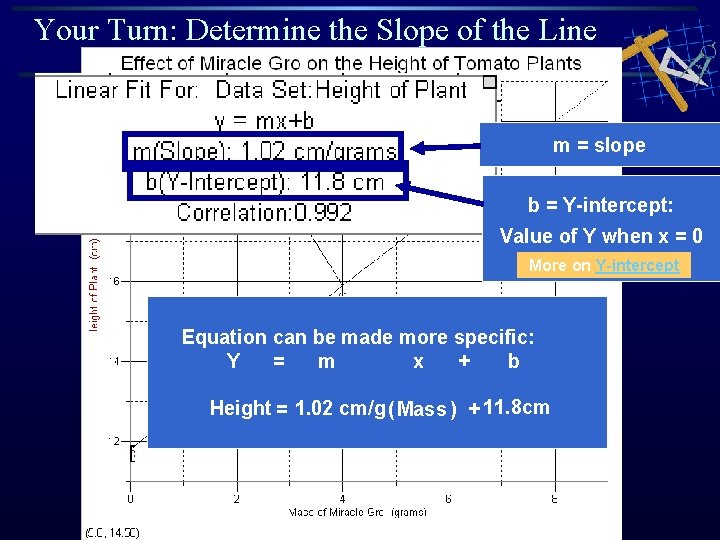
Your Turn: Determine the Slope of the Line m = slope b = Y-intercept: Value of Y when x = 0 More on Y-intercept Equation can be made more specific: Y = m x + b Height = 1. 02 cm/g ( Mass ) + 11. 8 cm

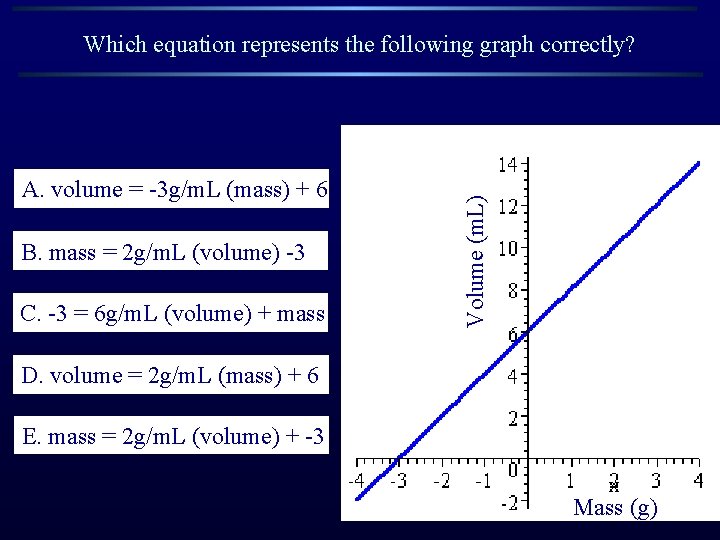
A. volume = -3 g/m. L (mass) + 6 B. mass = 2 g/m. L (volume) -3 C. -3 = 6 g/m. L (volume) + mass Volume (m. L) Which equation represents the following graph correctly? D. volume = 2 g/m. L (mass) + 6 E. mass = 2 g/m. L (volume) + -3 Mass (g)

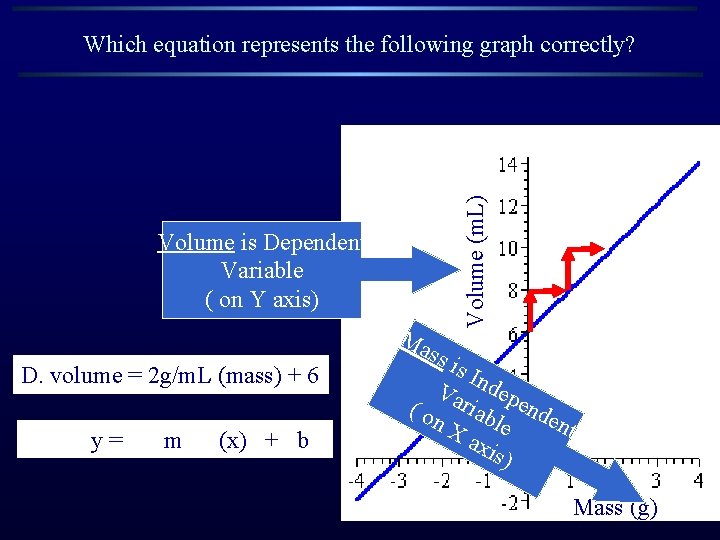
Volume is Dependent Variable ( on Y axis) D. volume = 2 g/m. L (mass) + 6 y= m (x) + b Ma ss i Volume (m. L) Which equation represents the following graph correctly? s In Va depe ( o riab nde n X le nt axi s) Mass (g)

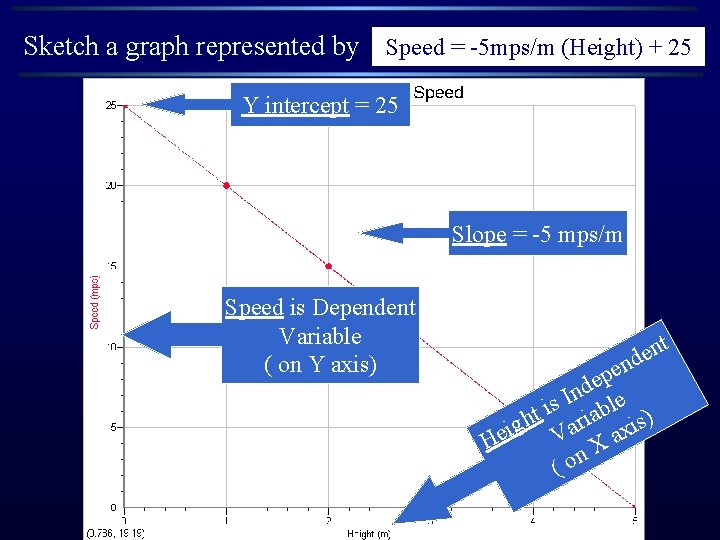
Sketch a graph represented by Speed = -5 mps/m (Height) + 25 Y intercept = 25 Slope = -5 mps/m Speed is Dependent Variable ( on Y axis) t n e nd e p e d n I s able i t h ari xis) g i V Xa He n (o

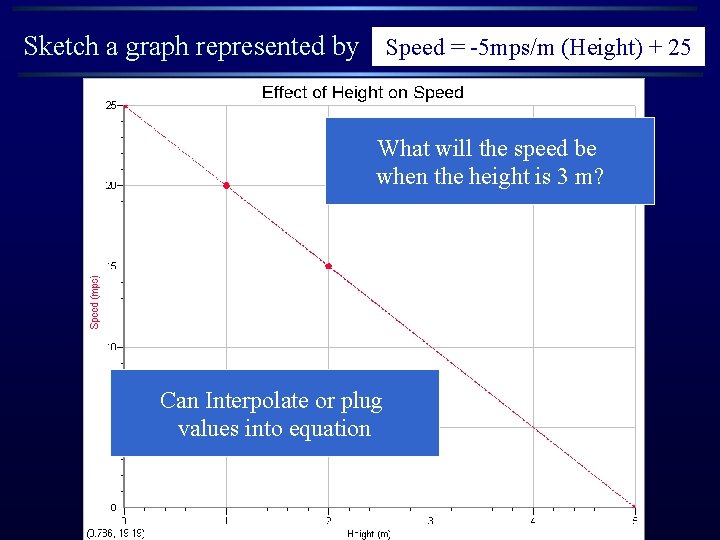
Sketch a graph represented by Speed = -5 mps/m (Height) + 25 What will the speed be when the height is 3 m? Can Interpolate or plug values into equation

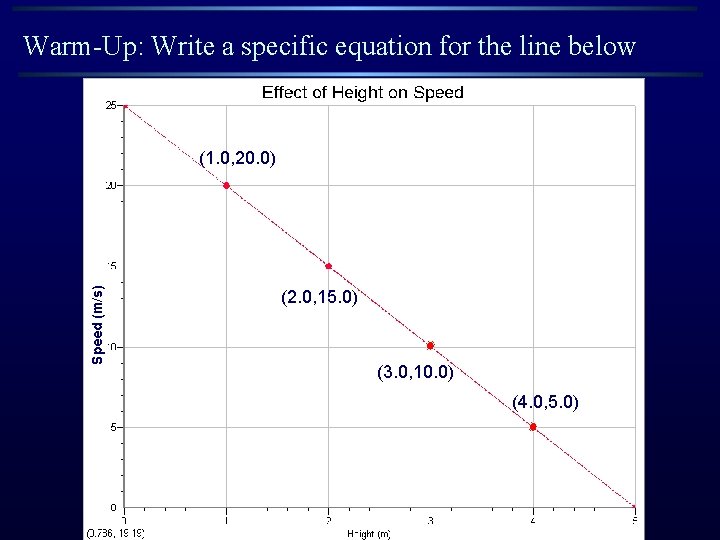
Warm-Up: Write a specific equation for the line below Speed (m/s) (1. 0, 20. 0) (2. 0, 15. 0) (3. 0, 10. 0) (4. 0, 5. 0)

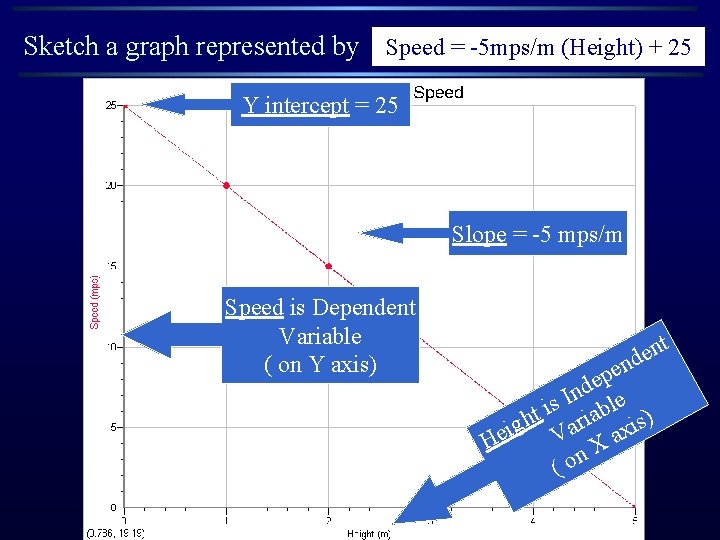
Sketch a graph represented by Speed = -5 mps/m (Height) + 25 Y intercept = 25 Slope = -5 mps/m Speed is Dependent Variable ( on Y axis) t n e nd e p e d n I s able i t h ari xis) g i V Xa He n (o

• The End

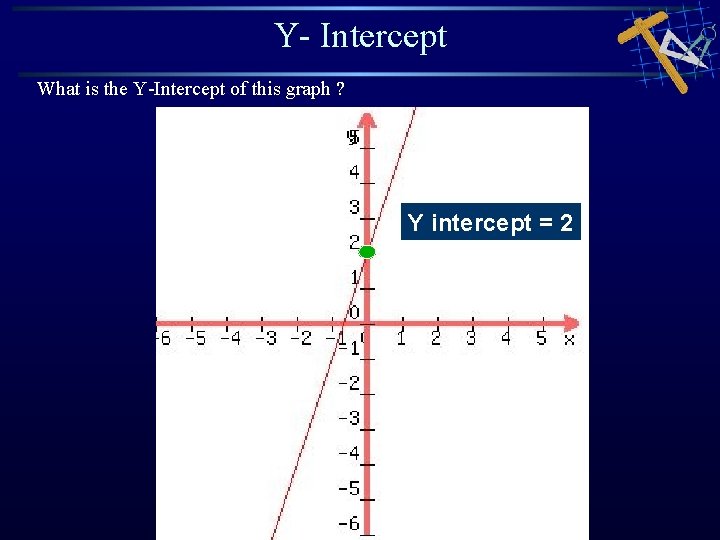
Y- Intercept What is the Y-Intercept of this graph ? Y intercept = 2

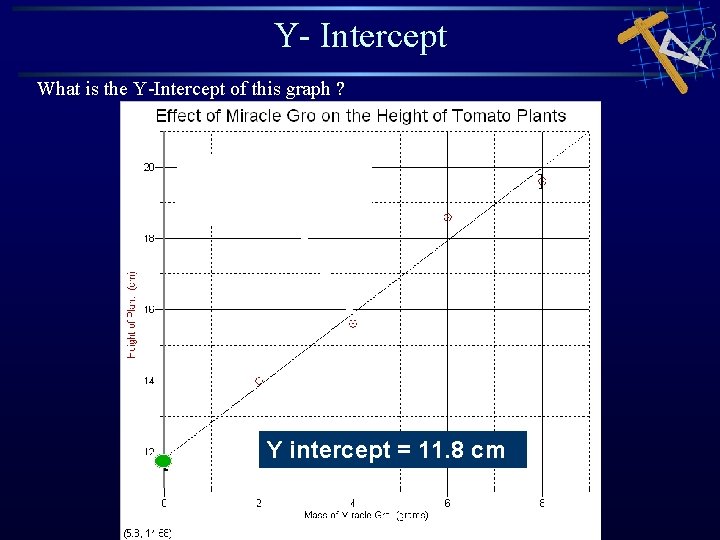
Y- Intercept What is the Y-Intercept of this graph ? Y intercept = 11. 8 cm

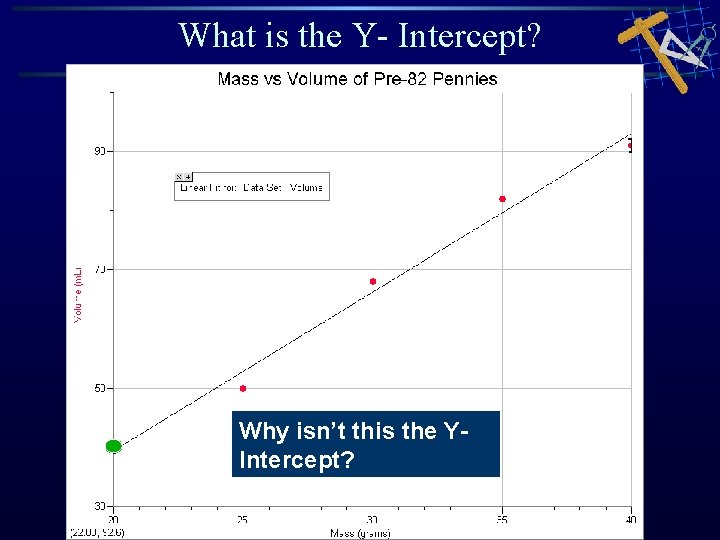
What is the Y- Intercept? Why isn’t this the YIntercept?

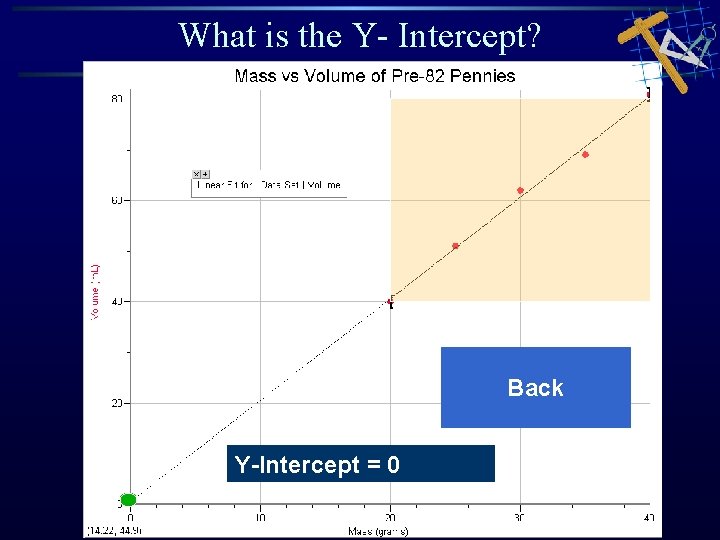
What is the Y- Intercept? Back Y-Intercept = 0