Makeup Labs Arrange with Victor in BSB117 Physics

Make-up Labs Arrange with Victor in BSB-117 Physics 1 D 03 - Lecture 31

Angular Momentum II • • General motion of a rigid body Collisions involving rotation Text Section 11. 1 -11. 6 Physics 1 D 03 - Lecture 31

Recall: • Angular momentum” is the rotational analogue of linear momentum. m v F p I w t L (“angular momentum”) L = Iw |L| = mrvt = mvr sin f Physics 1 D 03 - Lecture 31

Angular momentum of a particle: of a rotating rigid body: L = I w. In general, for a moving, rotating rigid body, The first term is called the “orbital” angular momentum and the second term is the “spin” angular momentum. Example: angular momentum of a planet about the sun. Physics 1 D 03 - Lecture 31

Example: The earth (m = 6. 0 x 1024 kg, R = 6400 km) moves at speed v = 30 km/s in an orbit of radius r = 150 x 106 km around the sun. It also spins on its axis once per day (ω = 7. 3 x 10 -5 rad/s). The angular momentum of the earth relative to the centre of the sun is L = mvr + ICM ω. The “orbital” part is calculated as if the earth were a particle orbiting the sun; then we add a the angular momentum or the spinning earth relative to its own centre of mass. Physics 1 D 03 - Lecture 31

Collisions: Collisions can conserve angular momentum as well as linear momentum. Total linear momentum is conserved if there is no external force during the collision (or if the external forces are small compared to the forces the colliding bodies exert on each other). Total angular momentum is conserved if there is no external torque during the collision (or if the external torques are small). Angular momentum may be calculated about any axis. Usually it is convenient to use an axis through the centre of mass, unless one of the colliding objects actually rotates about some other fixed axis. Physics 1 D 03 - Lecture 31

A metre stick (mass M, length L= 1 m, moment of inertia I ) is suspended from one end by a frictionless pivot at P. A ball of mass m, velocity v 0, strikes the other end of the (stationary) stick at right angles, and stops (final velocity of the ball is zero). P Question: Which of the following describe the motion of the stick after the collision? (Answer True, False, or Maybe for each one. ) A) B) C) D) ICM w = mv 0 L/2 IP w = mv 0 L Mv. CM = mv 0 ½ IP w 2= ½ mv 02 v 0 Physics 1 D 03 - Lecture 31

When the ball collides with the stick, there are two forces on the stick which momentarily are large: one from the ball (internal, if the system is ball plus stick); and one from the hinge at P (external force). So we should not expect momentum or angular momentum about the CM to be conserved. So A) and C) are false. P FP However there is no external torque about P, so angular momentum about P is conserved (so B is true). D) represents conservation of kinetic energy. It may be true, depending on whether the collision is elastic. Fball Physics 1 D 03 - Lecture 31

Quiz P A stick (uniform thin rod) is lying on the ice. A hockey puck hits the stick, at right angles, and the stick starts to slide. Point P is on the end farthest from where the puck hits. Immediately after the collision, the end P will start to move: CM A) B) C) D) in the same direction as v 0 in a direction opposite to v 0 at an angle (not 0 o or 180 o) to v 0 It depends where the puck hits v 0 Physics 1 D 03 - Lecture 31
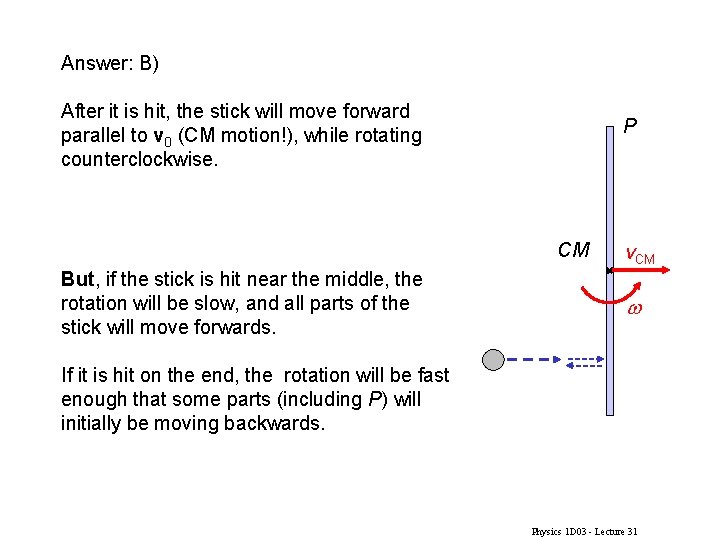
Answer: B) After it is hit, the stick will move forward parallel to v 0 (CM motion!), while rotating counterclockwise. P CM But, if the stick is hit near the middle, the rotation will be slow, and all parts of the stick will move forwards. v. CM w If it is hit on the end, the rotation will be fast enough that some parts (including P) will initially be moving backwards. Physics 1 D 03 - Lecture 31
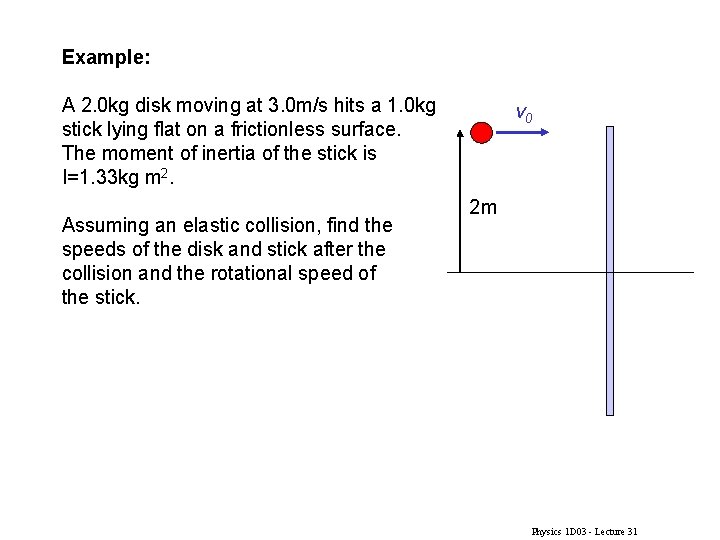
Example: A 2. 0 kg disk moving at 3. 0 m/s hits a 1. 0 kg stick lying flat on a frictionless surface. The moment of inertia of the stick is I=1. 33 kg m 2. Assuming an elastic collision, find the speeds of the disk and stick after the collision and the rotational speed of the stick. v 0 2 m Physics 1 D 03 - Lecture 31
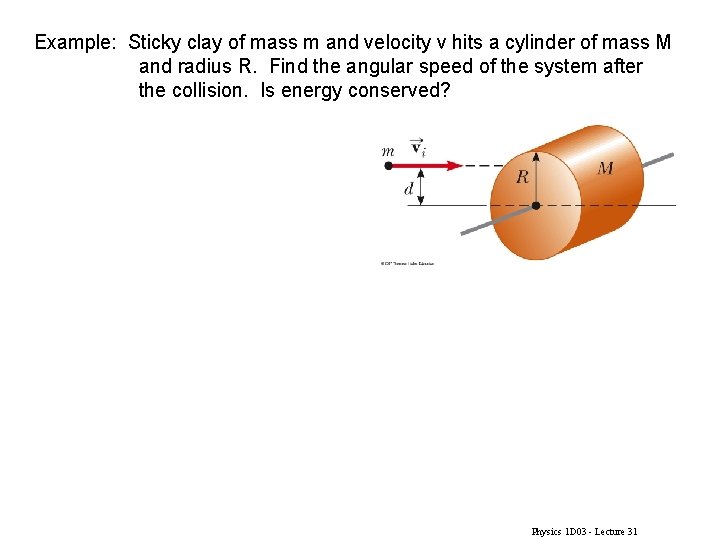
Example: Sticky clay of mass m and velocity v hits a cylinder of mass M and radius R. Find the angular speed of the system after the collision. Is energy conserved? Physics 1 D 03 - Lecture 31

Summary In general, for a rigid body, In collisions, angular momentum will be conserved it there is no external torque. Physics 1 D 03 - Lecture 31
- Slides: 13