Majorana Fermions and Topological Insulators Charles L Kane

Majorana Fermions and Topological Insulators Charles L. Kane, University of Pennsylvania I. Topological Band Theory - II. Integer Quantum Hall Effect 2 D Quantum Spin Hall Insulator 3 D Topological Insulator Topological Superconductor Majorana Fermions - Superconducting Proximity Effect on Topological Insulators - A route to topological quantum computing? Thanks to Gene Mele, Liang Fu, Jeffrey Teo

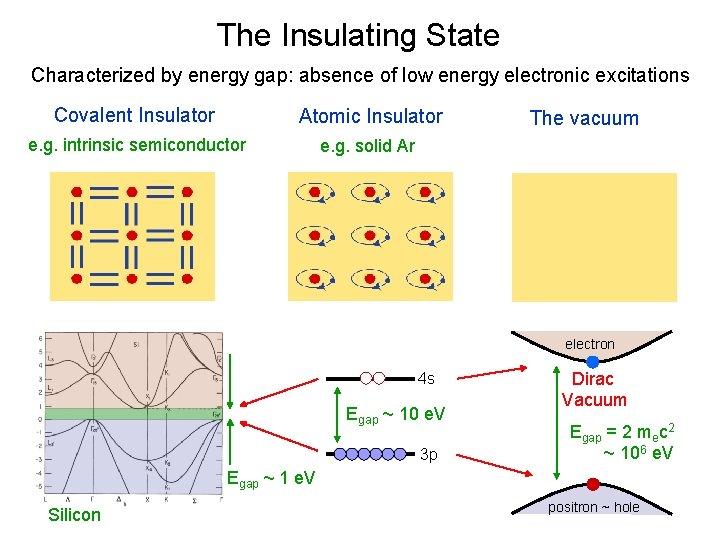
The Insulating State Characterized by energy gap: absence of low energy electronic excitations Covalent Insulator Atomic Insulator e. g. intrinsic semiconductor e. g. solid Ar The vacuum electron 4 s Egap ~ 10 e. V 3 p Dirac Vacuum Egap = 2 mec 2 ~ 106 e. V Egap ~ 1 e. V Silicon positron ~ hole

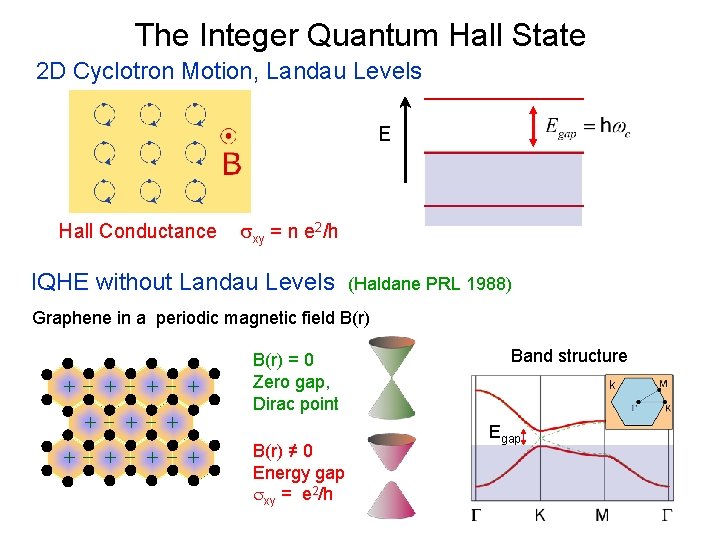
The Integer Quantum Hall State 2 D Cyclotron Motion, Landau Levels E Hall Conductance sxy = n e 2/h IQHE without Landau Levels (Haldane PRL 1988) Graphene in a periodic magnetic field B(r) +- + - + +- + - + B(r) = 0 Zero gap, Dirac point B(r) ≠ 0 Energy gap sxy = e 2/h Band structure k Egap

Topological Band Theory The distinction between a conventional insulator and the quantum Hall state is a topological property of the manifold of occupied states The set of occupied Bloch wavefunctions vector bundle over the torus. defines a U(N) Classified by the first Chern class (or TKNN invariant) (Thouless et al, 1984) Berry’s connection Berry’s curvature 1 st Chern class Trivial Insulator: n = 0 Quantum Hall state: sxy = n e 2/h The TKNN invariant can only change at a phase transition where the energy gap goes to zero

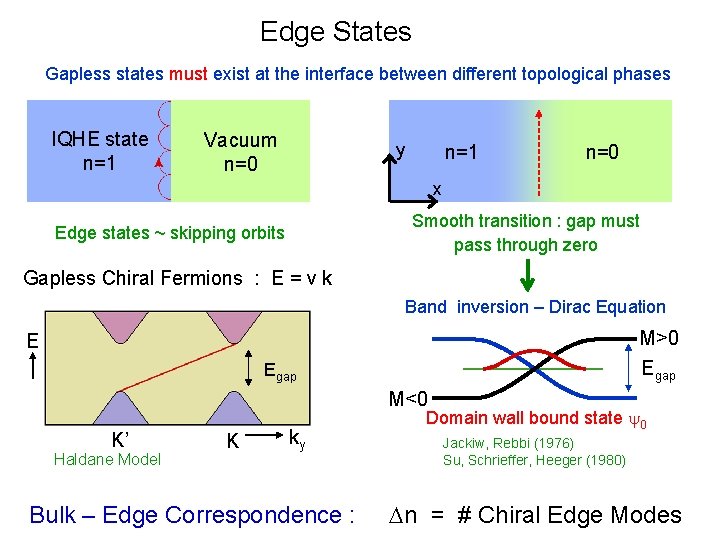
Edge States Gapless states must exist at the interface between different topological phases IQHE state n=1 Vacuum n=0 y n=1 n=0 x Smooth transition : gap must pass through zero Edge states ~ skipping orbits Gapless Chiral Fermions : E = v k Band inversion – Dirac Equation M>0 Egap E Egap M<0 K’ Haldane Model K ky Bulk – Edge Correspondence : Domain wall bound state y 0 Jackiw, Rebbi (1976) Su, Schrieffer, Heeger (1980) Dn = # Chiral Edge Modes

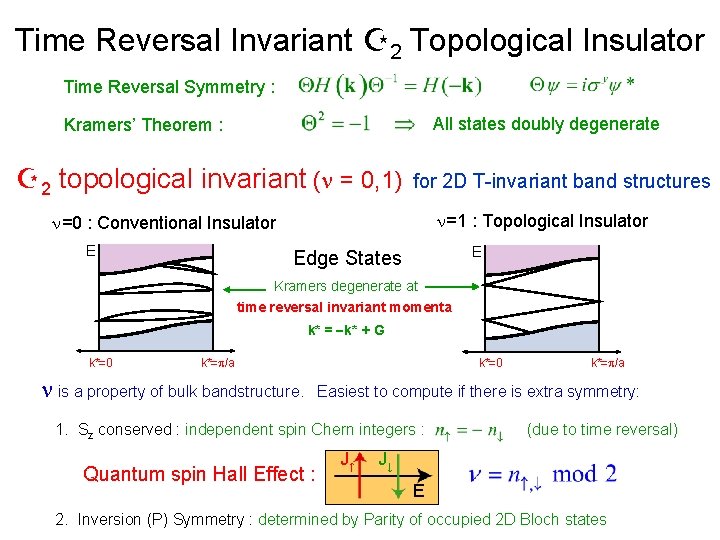
Time Reversal Invariant 2 Topological Insulator Time Reversal Symmetry : All states doubly degenerate Kramers’ Theorem : 2 topological invariant (n = 0, 1) for 2 D T-invariant band structures n=1 : Topological Insulator n=0 : Conventional Insulator E E Edge States Kramers degenerate at time reversal invariant momenta k* = -k* + G k*=0 k*=p/a n is a property of bulk bandstructure. k*=0 Easiest to compute if there is extra symmetry: 1. Sz conserved : independent spin Chern integers : Quantum spin Hall Effect : k*=p/a J↑ (due to time reversal) J↓ E 2. Inversion (P) Symmetry : determined by Parity of occupied 2 D Bloch states

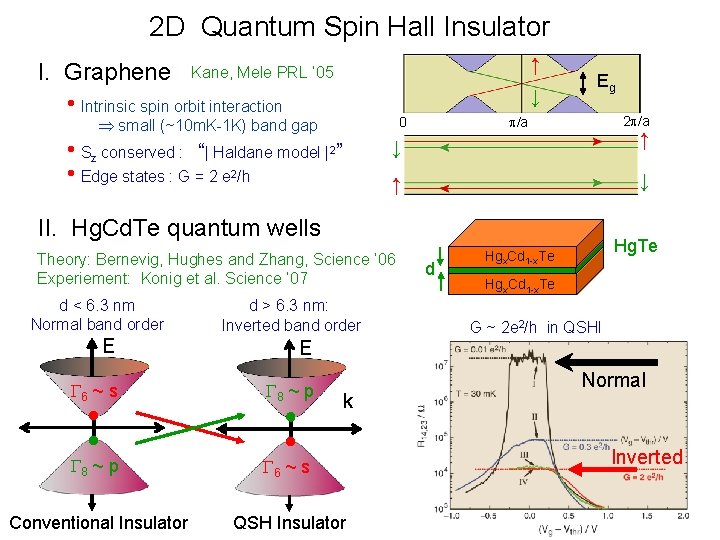
2 D Quantum Spin Hall Insulator I. Graphene ↑ Kane, Mele PRL ‘ 05 ↓ • Intrinsic spin orbit interaction p/a 0 small (~10 m. K-1 K) band gap • Sz conserved : “| Haldane model |2” • Edge states : G = 2 e 2/h Eg 2 p/a ↓ ↑ ↑ ↓ II. Hg. Cd. Te quantum wells Theory: Bernevig, Hughes and Zhang, Science ’ 06 Experiement: Konig et al. Science ‘ 07 d < 6. 3 nm Normal band order d > 6. 3 nm: Inverted band order E E G 6 ~ s G 8 ~ p G 6 ~ s Conventional Insulator QSH Insulator k d Hg. Te Hgx. Cd 1 -x. Te G ~ 2 e 2/h in QSHI Normal Inverted

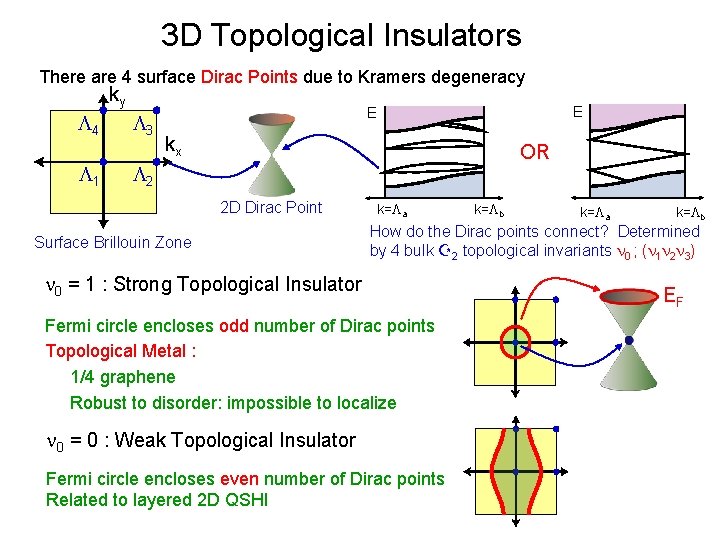
3 D Topological Insulators There are 4 surface Dirac Points due to Kramers degeneracy ky L 4 L 1 L 3 E E kx OR L 2 2 D Dirac Point Surface Brillouin Zone k=La k=Lb How do the Dirac points connect? Determined by 4 bulk 2 topological invariants n 0 ; (n 1 n 2 n 3) n 0 = 1 : Strong Topological Insulator Fermi circle encloses odd number of Dirac points Topological Metal : 1/4 graphene Robust to disorder: impossible to localize n 0 = 0 : Weak Topological Insulator Fermi circle encloses even number of Dirac points Related to layered 2 D QSHI EF

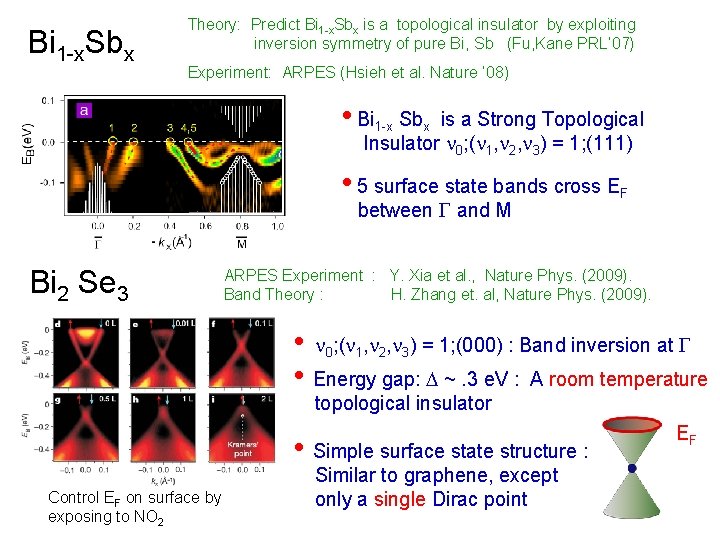
Bi 1 -x. Sbx Theory: Predict Bi 1 -x. Sbx is a topological insulator by exploiting inversion symmetry of pure Bi, Sb (Fu, Kane PRL’ 07) Experiment: ARPES (Hsieh et al. Nature ’ 08) • Bi 1 -x Sbx is a Strong Topological Insulator n 0; (n 1, n 2, n 3) = 1; (111) • 5 surface state bands cross EF between G and M Bi 2 Se 3 ARPES Experiment : Y. Xia et al. , Nature Phys. (2009). Band Theory : H. Zhang et. al, Nature Phys. (2009). • n 0; (n 1, n 2, n 3) = 1; (000) : Band inversion at G • Energy gap: D ~. 3 e. V : A room temperature topological insulator • Simple surface state structure : Control EF on surface by exposing to NO 2 Similar to graphene, except only a single Dirac point EF

Topological Superconductor, Majorana Fermions BCS mean field theory : Bogoliubov de Gennes Hamiltonian Particle-Hole symmetry : Quasiparticle redundancy : 1 D 2 Topological Superconductor : n = 0, 1 Discrete end state spectrum : E D 0 -D END n=0 “trivial” E -E (Kitaev, 2000) n=1 “topological” D 0 -D E=0 Majorana Fermion bound state “half a state”

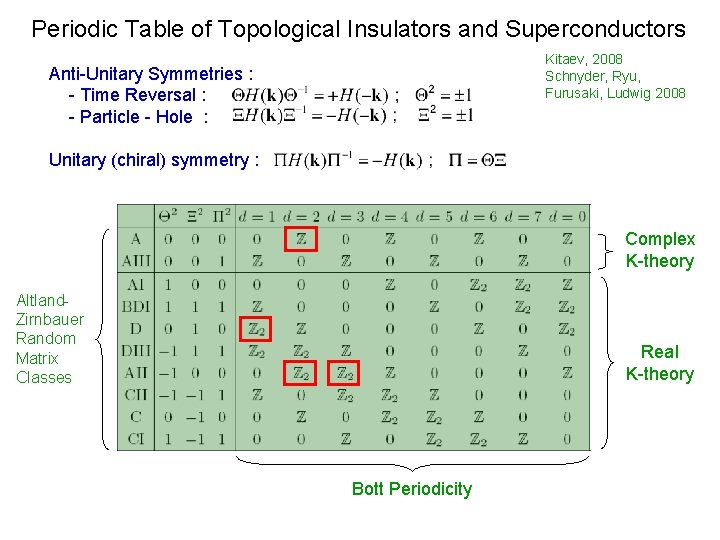
Periodic Table of Topological Insulators and Superconductors Kitaev, 2008 Schnyder, Ryu, Furusaki, Ludwig 2008 Anti-Unitary Symmetries : - Time Reversal : - Particle - Hole : Unitary (chiral) symmetry : Complex K-theory Altland. Zirnbauer Random Matrix Classes Real K-theory Bott Periodicity

Majorana Fermion : spin 1/2 particle = antiparticle ( g = g† ) Potential Hosts : Particle Physics : • Neutrino (maybe) Allows neutrinoless double b-decay. Condensed matter physics : Possible due to pair condensation • Quasiparticles in fractional Quantum Hall effect at n=5/2 • h/4 e vortices in p-wave superconductor Sr 2 Ru. O 4 • s-wave superconductor/ Topological Insulator. . . among others Current Status : NOT OBSERVED Topological Quantum Computing • • Kitaev, 2003 2 Majorana bound states = 1 fermion bound state - 2 degenerate states (full/empty) = 1 qubit 2 N separated Majoranas = N qubits Quantum Information is stored non locally - Immune from local sources of decoherence Adiabatic Braiding performs unitary operations - Non Abelian Statistics

Proximity effects : Engineering exotic gapped states on topological insulator surfaces m Dirac Surface States : Protected by Symmetry 1. Magnetic : (Broken Time Reversal Symmetry) • Orbital Magnetic field : • Zeeman magnetic field : • Half Integer quantized Hall effect : 2. Superconducting : Fu, Kane PRL 07 Qi, Hughes, Zhang PRB (08) M. ↑ T. I. (Broken U(1) Gauge Symmetry) proximity induced superconductivity • S-wave superconductor • Resembles spinless p+ip superconductor • Supports Majorana fermion excitations Fu, Kane PRL 08 S. C. T. I.

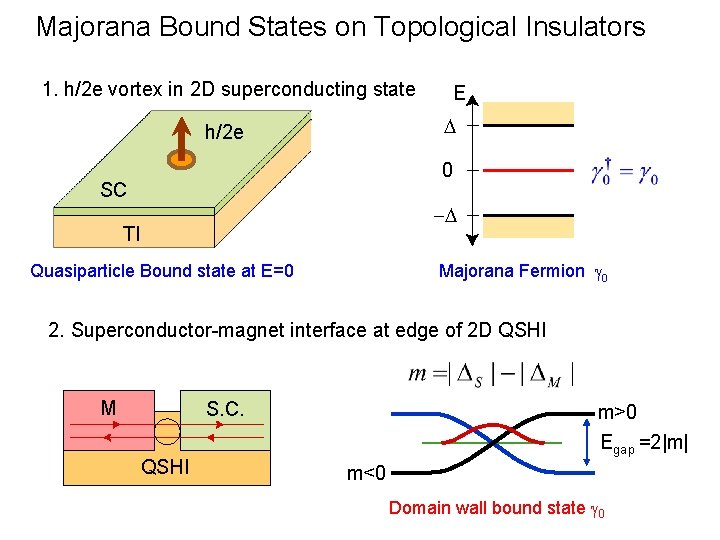
Majorana Bound States on Topological Insulators 1. h/2 e vortex in 2 D superconducting state E D h/2 e 0 SC -D TI Majorana Fermion g 0 Quasiparticle Bound state at E=0 2. Superconductor-magnet interface at edge of 2 D QSHI M S. C. QSHI m>0 Egap =2|m| m<0 Domain wall bound state g 0

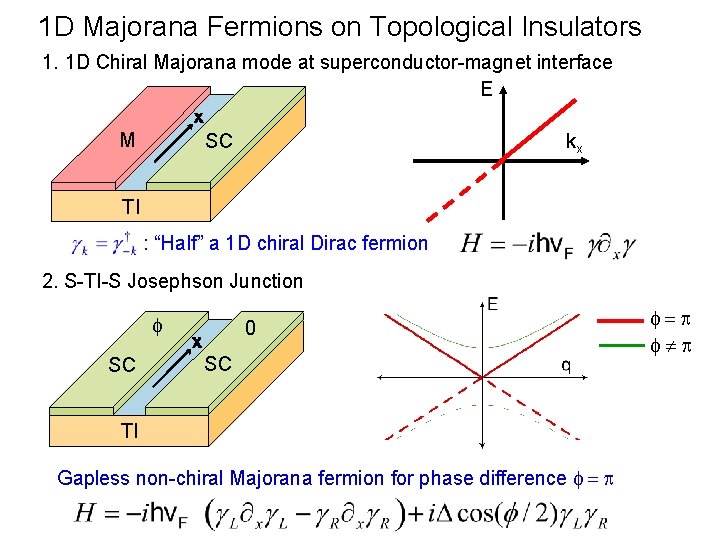
1 D Majorana Fermions on Topological Insulators 1. 1 D Chiral Majorana mode at superconductor-magnet interface E M SC kx TI : “Half” a 1 D chiral Dirac fermion 2. S-TI-S Josephson Junction f SC 0 SC TI Gapless non-chiral Majorana fermion for phase difference f = p f=p f p

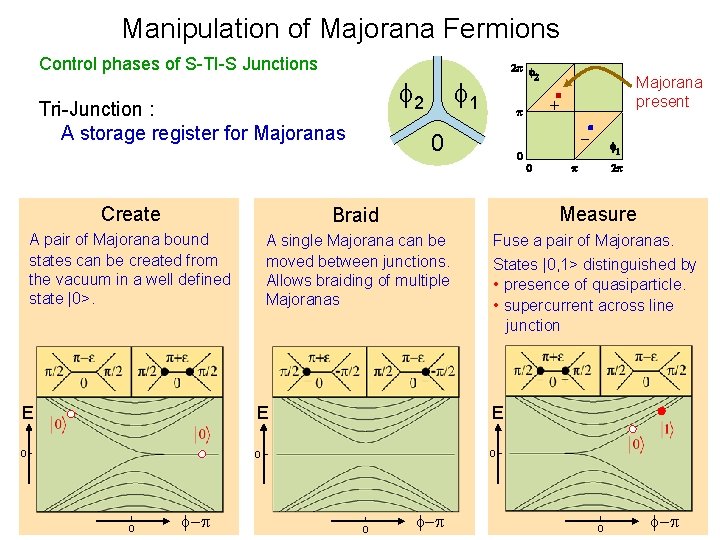
Manipulation of Majorana Fermions Control phases of S-TI-S Junctions f 1 f 2 Tri-Junction : A storage register for Majoranas Majorana present + - 0 Create Braid Measure A pair of Majorana bound states can be created from the vacuum in a well defined state |0>. A single Majorana can be moved between junctions. Allows braiding of multiple Majoranas Fuse a pair of Majoranas. States |0, 1> distinguished by • presence of quasiparticle. • supercurrent across line junction E E E 0 0 f-p

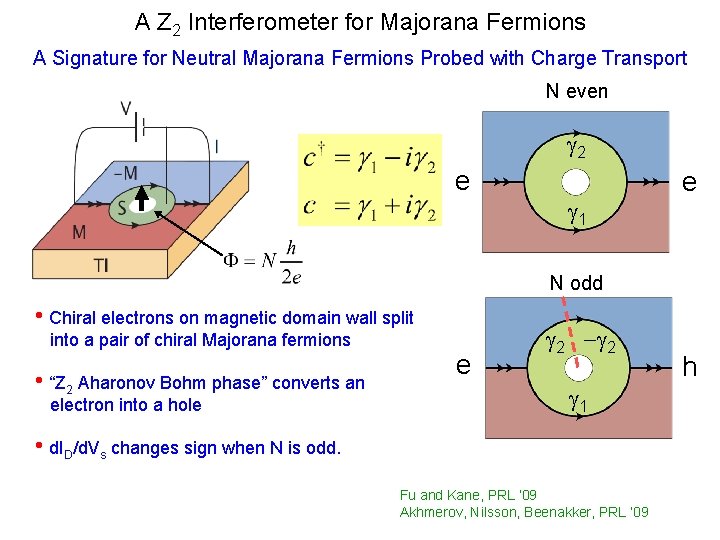
A Z 2 Interferometer for Majorana Fermions A Signature for Neutral Majorana Fermions Probed with Charge Transport N even g 2 e g 1 e N odd • Chiral electrons on magnetic domain wall split into a pair of chiral Majorana fermions • “Z 2 Aharonov Bohm phase” converts an electron into a hole e g 2 -g 2 g 1 • d. ID/d. Vs changes sign when N is odd. Fu and Kane, PRL ‘ 09 Akhmerov, Nilsson, Beenakker, PRL ‘ 09 h

Conclusion • • A new electronic phase of matter has been predicted and observed - 2 D : Quantum spin Hall insulator in Hg. Cd. Te QW’s - 3 D : Strong topological insulator in Bi 1 -x. Sbx , Bi 2 Se 3, Bi 2 Te 3 Superconductor/Topological Insulator structures host Majorana Fermions - A Platform for Topological Quantum Computation Experimental Challenges - Charge and Spin transport Measurements on topological insulators - Superconducting structures : - Create, Detect Majorana bound states - Magnetic structures : - Create chiral edge states, chiral Majorana edge states - Majorana interferometer Theoretical Challenges - Further manifestations of Majorana fermions and non-Abelian states - Effects of disorder and interactions on surface states