Major Numeric Data Types Unsigned Integers Signed Integers

Major Numeric Data Types • Unsigned Integers • Signed Integers • Alphanumeric Data – ASCII & UNICODE • Floating Point Numbers

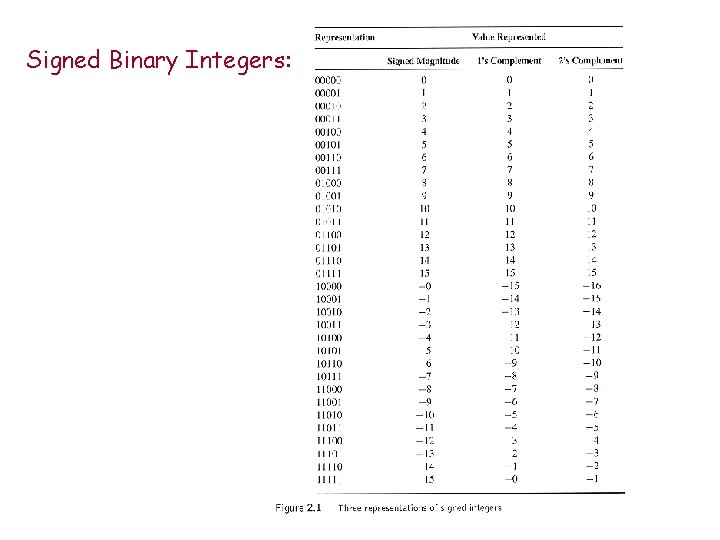
Signed Binary Integers:

2’s Complement Arithmetic • Addition • Subtraction • Multiplication, Division

Overflow Adding two numbers which results In a sum that is too large to store: A+B A-B

Alphanumeric Data Representation: ASCII Code Table (7 bit) Packed? Unpacked? UNICODE (16 bit) - UTF-8 provides a 16 bit superset of ASCII

Floating Point Numbers Example: -56. 67534 x 10 -5 • Sign • Fraction • Exponent

Single Precision Floating Point Numbers IEEE Standard 32 bit Single Precision Floating Point Numbers are stored as: S EEEE FFFFFFFFFFFF S: Sign – 1 bit E: Exponent – 8 bits F: Fraction – 23 bits The value V: • If E=255 and F is nonzero, then V= Na. N ("Not a Number") • If E=255 and F is zero and S is 1, then V= - Infinity • If E=255 and F is zero and S is 0, then V= Infinity • If 0<E<255 then V= (-1)**S * 2 ** (E-127) * (1. F) (exponent range = -127 to +128) • If E=0 and F is nonzero, then V= (-1)**S * 2 ** (-126) * (0. F) ("unnormalized" values”) • If E=0 and F is zero and S is 1, then V= - 0 • If E=0 and F is zero and S is 0, then V = 0 Note: 255 decimal = 1111 in binary (8 bits)

Double Precision Floating Point Numbers IEEE Standard 64 bit Double Precision Floating Point Numbers are stored as: S EEEEEE FFFFFFFFFFFFFFFFFFFFFFFFFF S: Sign – 1 bit E: Exponent – 11 bits F: Fraction – 52 bits The value V: • If E=2047 and F is nonzero, then V= Na. N ("Not a Number") • If E=2047 and F is zero and S is 1, then V= - Infinity • If E=2047 and F is zero and S is 0, then V= Infinity • If 0<E<2047 then V= (-1)**S * 2 ** (E-1023) * (1. F) (exponent range = -1023 to +1024) • If E=0 and F is nonzero, then V= (-1)**S * 2 ** (-1022) * (0. F) ("unnormalized" values) • If E=0 and F is zero and S is 1, then V= - 0 • If E=0 and F is zero and S is 0, then V= 0 Note: 2047 decimal = 111111 in binary (11 bits)

Underflow A calculation in floating point that results in a result that is “essentially” zero, i. e. too small to represent in floating point notation.

Round off Errors due to inherent imprecision of computers / computation

Chapter 3 Digital Logic Structures • The Transistor • CMOS Devices • Implementing Logic with CMOS Devices • Combinational Logic Circuits • Decoders • Mux’s • Full Adder • PLA’s

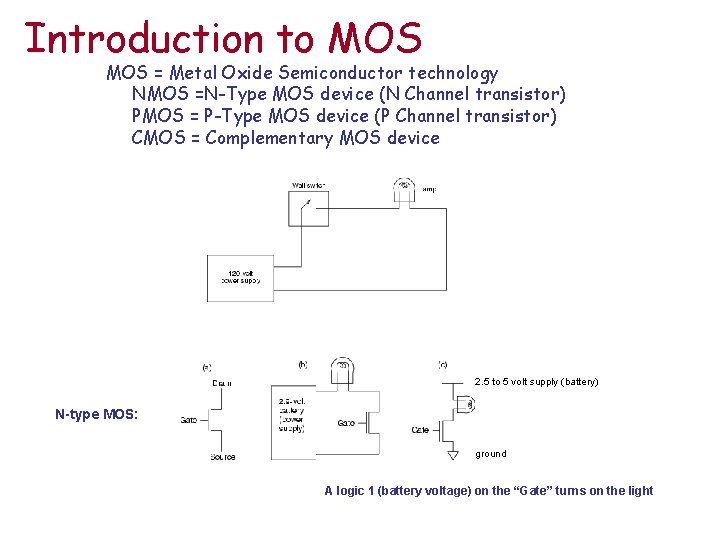
Introduction to MOS = Metal Oxide Semiconductor technology NMOS =N-Type MOS device (N Channel transistor) PMOS = P-Type MOS device (P Channel transistor) CMOS = Complementary MOS device 2. 5 to 5 volt supply (battery) N-type MOS: ground A logic 1 (battery voltage) on the “Gate” turns on the light

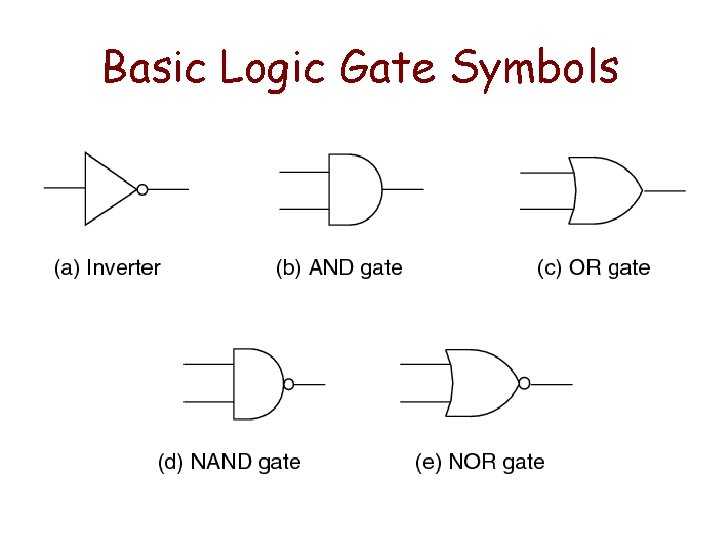
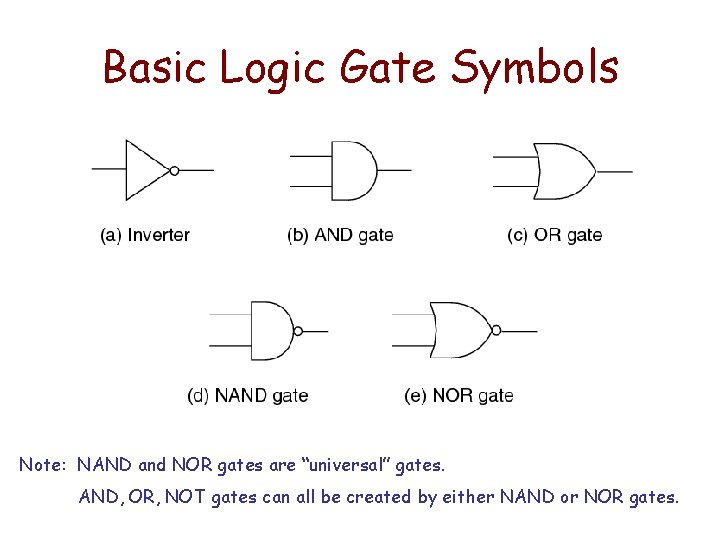
Basic Logic Gate Symbols

N-Type MOS Devices

P-Type MOS Devices

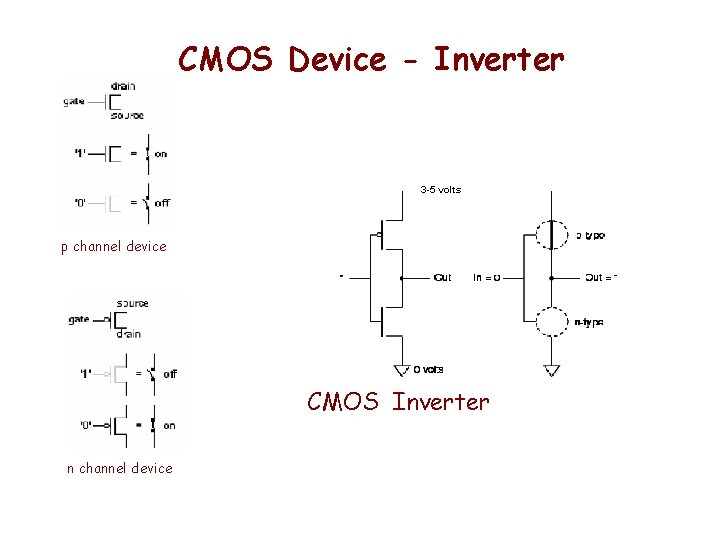
CMOS Device - Inverter 3 -5 volts p channel device CMOS Inverter n channel device

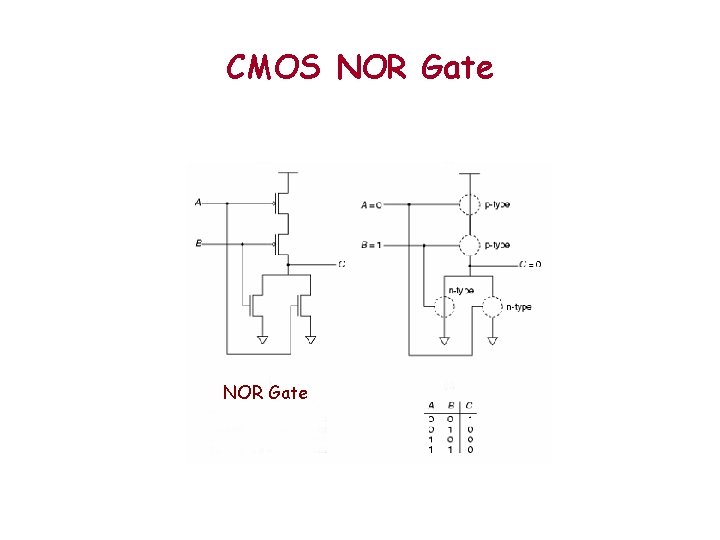
CMOS NOR Gate

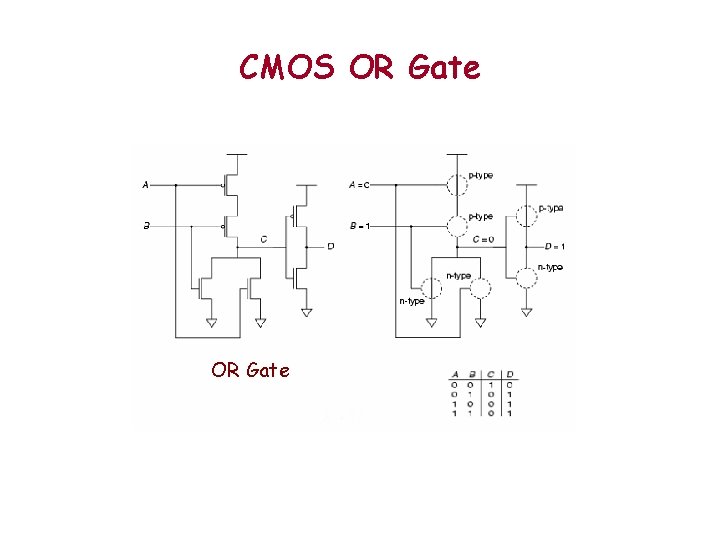
CMOS OR Gate

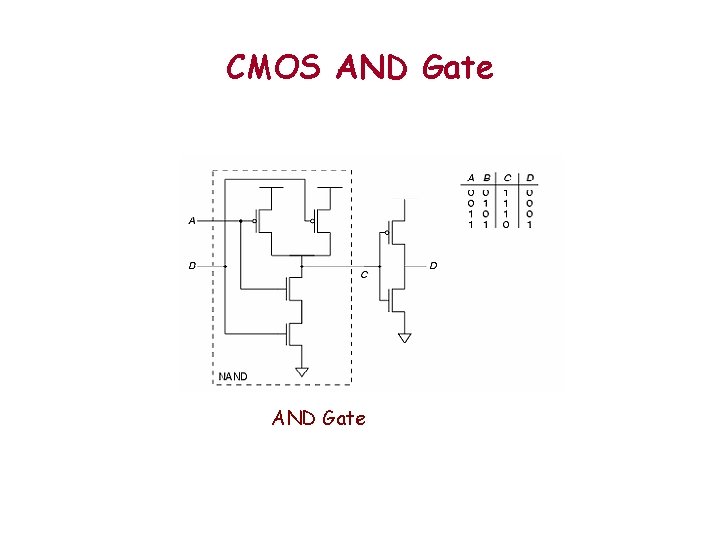
CMOS AND Gate

Basic Logic Gate Symbols Note: NAND and NOR gates are “universal” gates. AND, OR, NOT gates can all be created by either NAND or NOR gates.

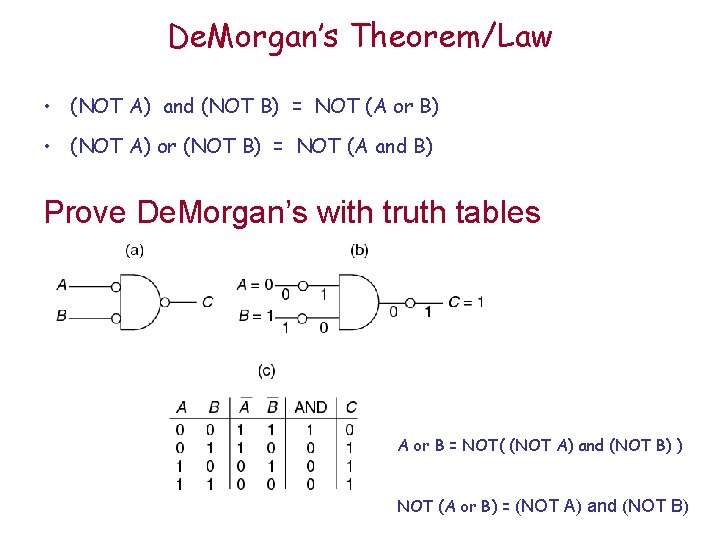
De. Morgan’s Theorem/Law • (NOT A) and (NOT B) = NOT (A or B) • (NOT A) or (NOT B) = NOT (A and B) Prove De. Morgan’s with truth tables A or B = NOT( (NOT A) and (NOT B) ) NOT (A or B) = (NOT A) and (NOT B)