Major Numeric Data Types Unsigned Integers Signed Integer

Major Numeric Data Types • Unsigned Integers • Signed Integer • Alphanumeric Data – ASCII & UNICODE • Floating Point Numbers

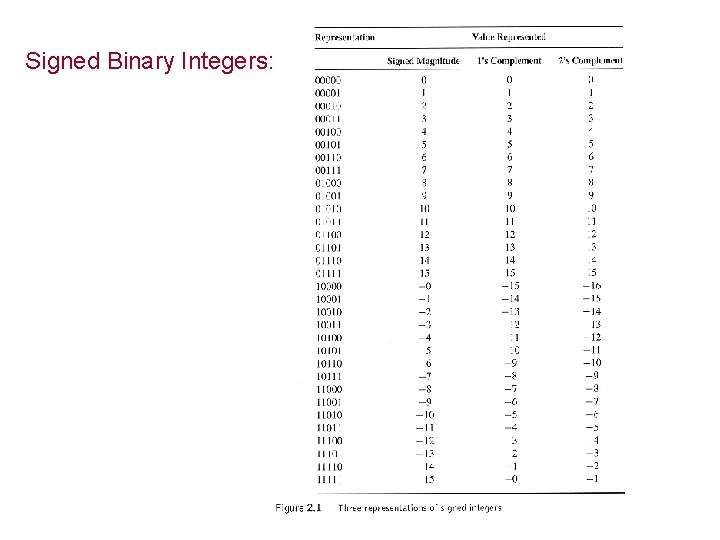
Become proficient with binary number representation • Unsigned binary Integers • Signed Binary Integers (see Text Figure 2. 1) • 1’s Complement Binary Integers • 2’s complement Binary Integers • The binary point (what does it mean? )

Signed Binary Integers:

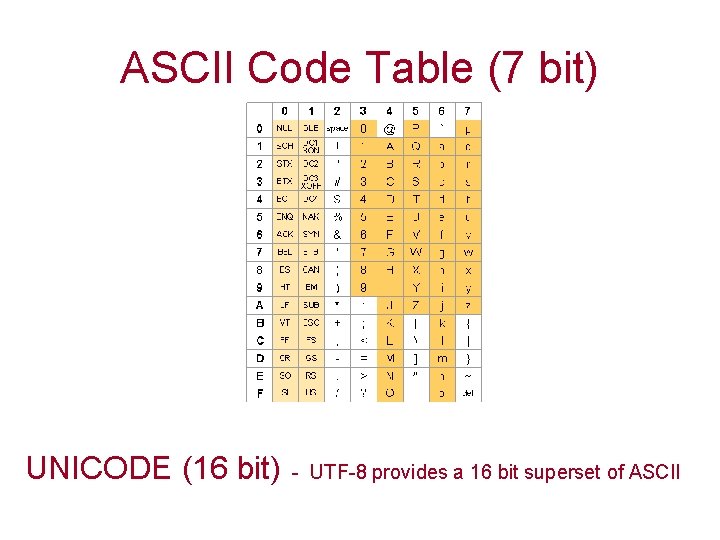
ASCII Code Table (7 bit) UNICODE (16 bit) - UTF-8 provides a 16 bit superset of ASCII

Floating Point Numbers Example: -56. 67534 x 10 -5 • Sign • Fraction • Exponent

Single Precision Floating Point Numbers IEEE Standard Single Precision Floating Point Numbers are 32 bits long: S EEEE FFFFFFFFFFFF Sign – 1 bit Exponent – 8 bits Fraction – 23 bits The value V: • If E=255 and F is nonzero, then V= Na. N ("Not a number") • If E=255 and F is zero and S is 1, then V= - Infinity • If E=255 and F is zero and S is 0, then V= Infinity • If 0<E<255 then V= (-1)**S * 2 ** (E-127) * (1. F) • If E=0 and F is nonzero, then V= (-1)**S * 2 ** (-126) * (0. F) ("unnormalized" values”) • If E=0 and F is zero and S is 1, then V= - 0 • If E=0 and F is zero and S is 0, then V = 0

Double Precision Floating Point Numbers IEEE Standard Double Precision Floating Point Numbers are 64 bits long: S EEEEEE FFFFFFFFFFFFFFFFFFFFFFFFFF Sign – 1 bit Exponent – 11 bits Fraction – 52 bits The value V: • If E=2047 and F is nonzero, then V= Na. N ("Not a number") • If E=2047 and F is zero and S is 1, then V= - Infinity • If E=2047 and F is zero and S is 0, then V= Infinity • If 0<E<2047 then V= (-1)**S * 2 ** (E-1023) * (1. F) • If E=0 and F is nonzero, then V= (-1)**S * 2 ** (-1022) * (0. F) ("unnormalized" values) • If E=0 and F is zero and S is 1, then V= - 0 • If E=0 and F is zero and S is 0, then V= 0

2’s Complement Sign Extention • Positive numbers • Negative numbers

2’s Complement Arithmetic • Addition • Subtraction • Multiplication, Division ?

Round off Errors due to inherent imprecision of computers / computation

Overflow Adding two numbers which results In a sum that is too large to store: A+B A-B

Underflow A calculation in floating point that results in an intermediate result that is essentially zero.

Binary Logic • AND • OR • NOT • NAND • NOR • XOR • Truth tables • De. Morgan’s Theorem • Bit vectors