Maintaining Stream Statistics over Sliding Windows Ariel Rosenfeld

Streams Here, There, Everywhere! 1 1 Network Traffic Engineering. 0 0 Call Record Analysis.

Sliding Window Model Time Increases …. 1 0 0 0 1 1 1 1

The Problem –Basic counting Count the number of ones in N size window. Exact

Sliding Window Computation Main difficulty: discount expiring data ◦ As each element arrives, one

Results Exponential Histogram (EH): ◦ 1 + ε approximation. (k = 1/ε) ◦ Space:

Example k/2 = 1. Bucket sizes = 4, 2, 2, 1. 4, 2, 2,

Observations Error in last (leftmost) bucket. Bucket Sizes (left to right): Cm, Cm-1, …,

Observations Every Bucket will become last bucket in future. New elements may be all

Invariant Maintain Ci/2(Ci-1+…+C 2+C 1+1) <= 1/k. Exponentially increasing bucket sizes from right to

Guarantees. Error Guarantee: ◦ Error <= Cm/2(Cm-1+…+C 2+C 1) <= 1/k. Number of buckets:

Random Counter If exact size of bucket is not “a must”. Number of buckets:

Slides: 13

Download presentation

Maintaining Stream Statistics over Sliding Windows Ariel Rosenfeld 1

Streams Here, There, Everywhere! 1 1 Network Traffic Engineering. 0 0 Call Record Analysis. 1 Sensor Data Analysis. 0 Medical, Financial Monitoring. Etc, etc. 1 0 1 1 1 2

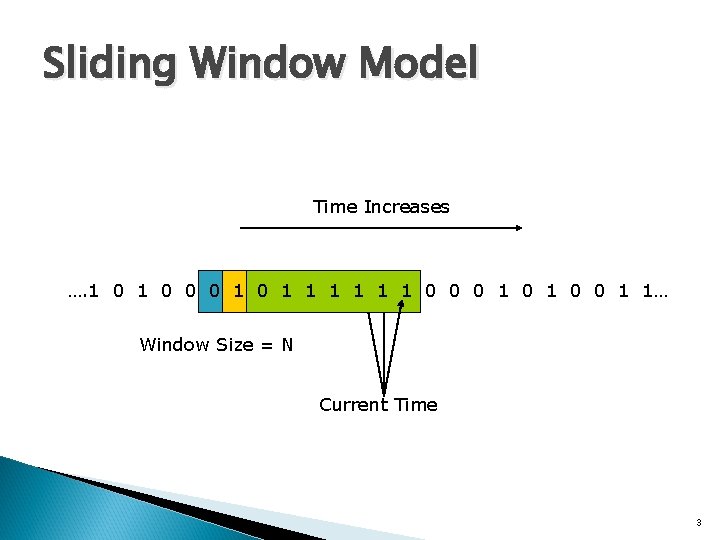
Sliding Window Model Time Increases …. 1 0 0 0 1 1 1 1 0 0 0 1 1… Window Size = N Current Time 3

The Problem –Basic counting Count the number of ones in N size window. Exact Solution: Θ(N) memory. Approximate Solution: ? ◦ Good approx with o(N) memory? 4

Sliding Window Computation Main difficulty: discount expiring data ◦ As each element arrives, one element expires value of expiring element can’t be known exectly. ◦ How do we update our structure? One solution: Use Histograms … 1 1 0 1 0 0 0 1 0 Bucket sums = (3, 2, 1, 2) 5

Results Exponential Histogram (EH): ◦ 1 + ε approximation. (k = 1/ε) ◦ Space: O(1/ε(log 2 N)) bits. ◦ Time: O(log N) worst case, O(1) amortized. 6

Histograms (remainder) 7

Example k/2 = 1. Bucket sizes = 4, 2, 2, 1. 4, 2, 2, 2, 1. 4, 4, 2, 1. 4, 2, 2, 1, 1, 1. …. 1 1 0 1 0 1 0 1 1… Future Element arrived this step. 8

Observations Error in last (leftmost) bucket. Bucket Sizes (left to right): Cm, Cm-1, …, C 2, C 1 Absolute Error <= Cm/2. Answer >= Cm-1+…+C 2+C 1+1. Error <= Cm/2(Cm-1+…+C 2+C 1+1). Maintain: Cm/2(Cm-1+…+C 2+C 1+1) <= 1/k. 9

Observations Every Bucket will become last bucket in future. New elements may be all zeros. Bucket Sizes (left to right): Cm, Cm-1, …, C 2, C 1 For every bucket i, ◦ Ci/2(Ci-1+…+C 2+C 1+1) <= 1/k. 10

Invariant Maintain Ci/2(Ci-1+…+C 2+C 1+1) <= 1/k. Exponentially increasing bucket sizes from right to left. At least k/2 buckets (at most k/2 +1)of each size(1, 2, 4, 8, …, 2 i, . . . ). 11

Guarantees. Error Guarantee: ◦ Error <= Cm/2(Cm-1+…+C 2+C 1) <= 1/k. Number of buckets: O(k log N). Buckets require O(log N) bits. Total memory: O(k log 2 N) bits. 12

Random Counter If exact size of bucket is not “a must”. Number of buckets: O(k log N). Buckets require O(loglog N) bits. Total memory: O(k log. N loglog. N) bits. 13