Main Idea Key Concept Multiply Integers with Different

  • Slides: 20
Download presentation

Main Idea Key Concept: Multiply Integers with Different Signs Example 1: Multiply Integers with

Main Idea Key Concept: Multiply Integers with Different Signs Example 1: Multiply Integers with Different Signs Example 2: Multiply Integers with Different Signs Key Concept: Multiply Integers with the Same Sign Example 3: Multiply Integers with the Same Sign Example 4: Multiply Integers with the Same Sign Example 5: Multiply Integers with the Same Sign Example 6: Real-World Example 7: Add Integers with the Same Sign

• Use the rules for multiplying integers.

• Use the rules for multiplying integers.

Multiply Integers with Different Signs Find 5(– 4) = – 20 Answer: – 20

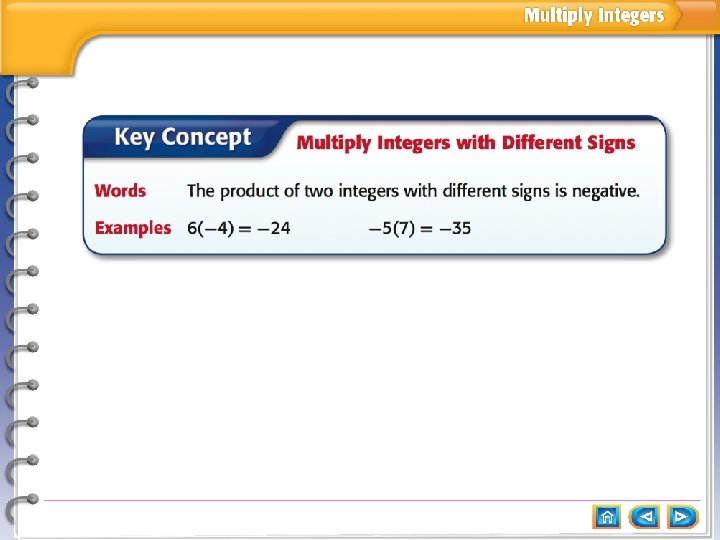
Multiply Integers with Different Signs Find 5(– 4) = – 20 Answer: – 20 The integers have different signs. The product is negative.

Find 2(– 7). A. – 14 B. – 9 C. – 5 D. 14

Find 2(– 7). A. – 14 B. – 9 C. – 5 D. 14

Multiply Integers with Different Signs Find – 3(9) = – 27 Answer: – 27

Multiply Integers with Different Signs Find – 3(9) = – 27 Answer: – 27 The integers have different signs. The product is negative.

Find – 2(11). A. 22 B. 13 C. – 13 D. – 22

Find – 2(11). A. 22 B. 13 C. – 13 D. – 22

Multiply Integers with the Same Sign Find – 6(– 8) = 48 Answer: 48

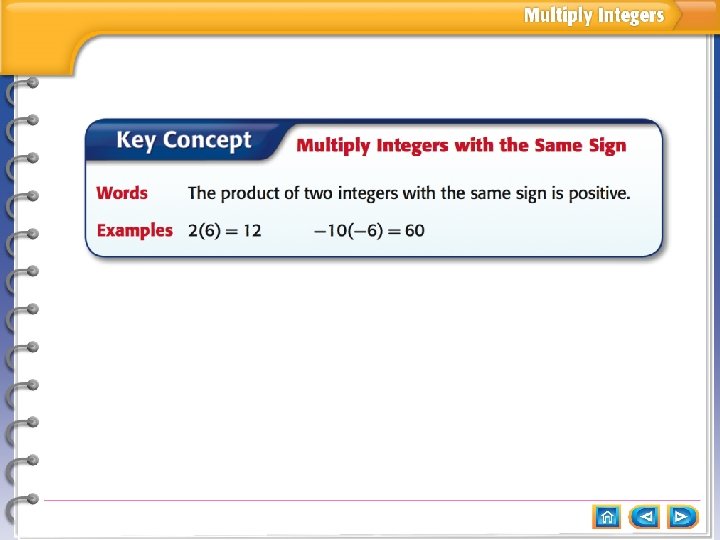
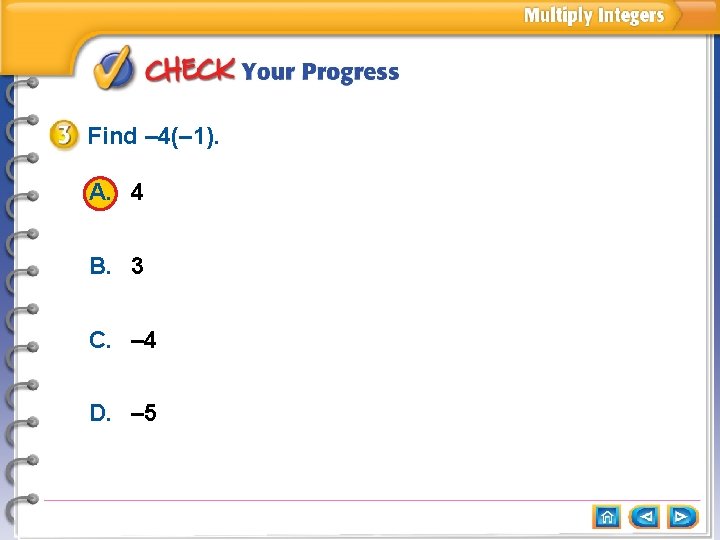
Multiply Integers with the Same Sign Find – 6(– 8) = 48 Answer: 48 The integers have the same sign. The product is positive.

Multiply Integers with the Same Sign Find (– 8)2 = (– 8) = 64

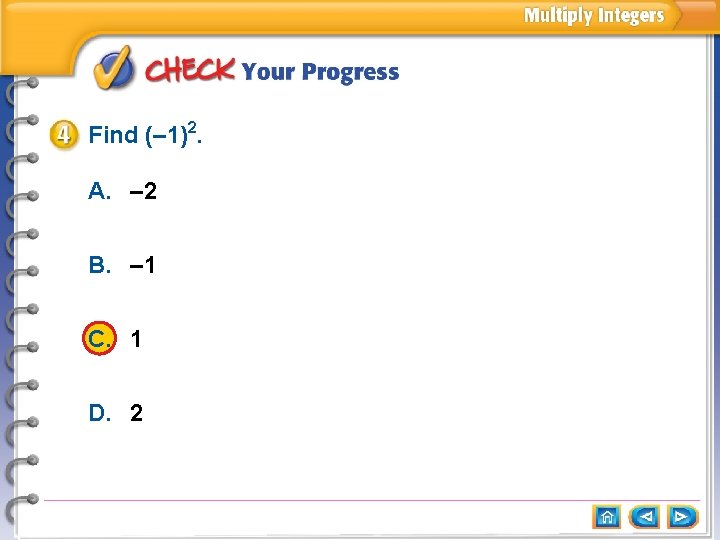
Multiply Integers with the Same Sign Find (– 8)2 = (– 8) = 64 Answer: 64 There are two factors of – 8. The product is positive.

Find (– 1)2. A. – 2 B. – 1 C. 1 D. 2

Find (– 1)2. A. – 2 B. – 1 C. 1 D. 2

Multiply Integers with the Same Sign Find – 2(– 5)(– 6) = [– 2(–

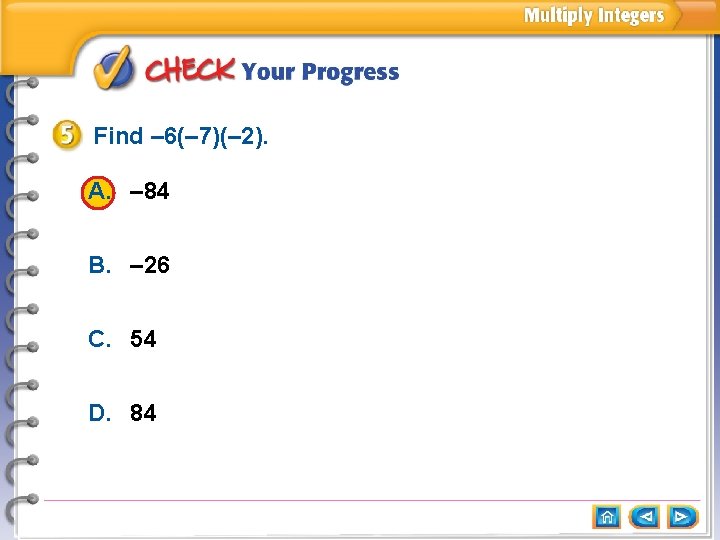
Multiply Integers with the Same Sign Find – 2(– 5)(– 6) = [– 2(– 5)](– 6)] Associative Property = 10(– 6) – 2(– 5) = 10 = – 60 10(– 6) = – 60 Answer: – 60

Find – 6(– 7)(– 2). A. – 84 B. – 26 C. 54 D.

Find – 6(– 7)(– 2). A. – 84 B. – 26 C. 54 D. 84

MINES A mine elevator descends at a rate of 300 feet per minute. How

MINES A mine elevator descends at a rate of 300 feet per minute. How far below Earth’s surface will the elevator be after 5 minutes? If the elevator descends 300 feet per minute then after 5 minutes the mine elevator will be at 5(– 300) or – 1, 500 feet. The mine elevator will descend to 1, 500 feet below the Earth’s surface. Answer: – 1, 500 feet or 1, 500 feet below Earth’s surface

FOOD John’s freezer decreases the temperature of a casserole by 3ºF every minute. What

FOOD John’s freezer decreases the temperature of a casserole by 3ºF every minute. What is the change in temperature after 10 minutes? A. +30ºF B. +13ºF C. – 13ºF D. – 30ºF

Evaluating Expressions ALGEBRA Evaluate abc if a = – 3, b = 5, and

Evaluating Expressions ALGEBRA Evaluate abc if a = – 3, b = 5, and c = – 8. abc = – 3(5)(– 8) Replace a with – 3, b with 5, and c with – 8. = (– 15)(– 8) Multiply – 3 and 5. = 120 Multiply – 15 and – 8. Answer: The solution is 120.

ALGEBRA Evaluate rst if r = – 1, s = 2, and t =

ALGEBRA Evaluate rst if r = – 1, s = 2, and t = – 6. A. – 12 B. – 11 C. 11 D. 12