Magnetism AP Physics C Facts about Magnetism Magnets

Magnetism AP Physics C

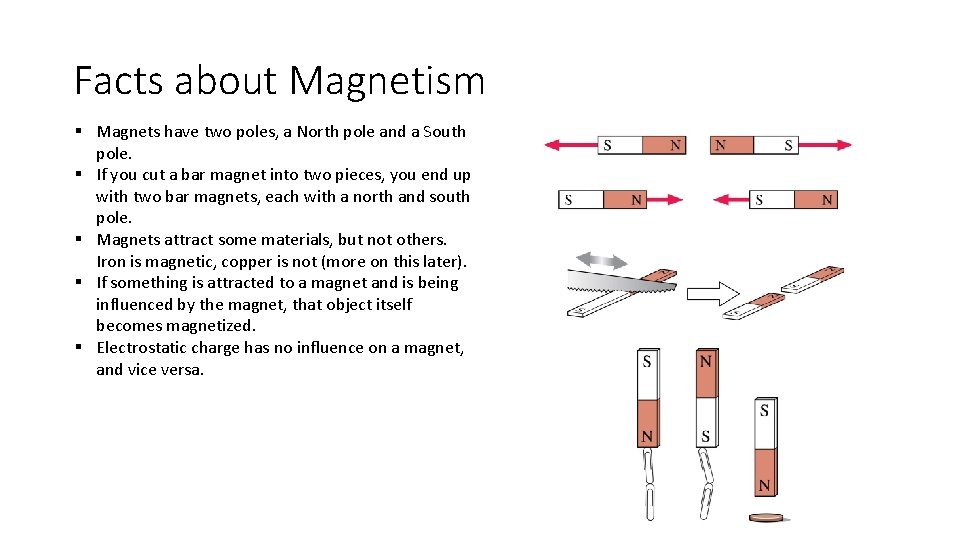
Facts about Magnetism § Magnets have two poles, a North pole and a South pole. § If you cut a bar magnet into two pieces, you end up with two bar magnets, each with a north and south pole. § Magnets attract some materials, but not others. Iron is magnetic, copper is not (more on this later). § If something is attracted to a magnet and is being influenced by the magnet, that object itself becomes magnetized. § Electrostatic charge has no influence on a magnet, and vice versa.

Magnetic Fields § Like with electricity, we will use the field model to explain magnetic phenomena. § Magnetic field lines leave the north pole of a magnet and enter the south pole. § Magnetic field lines are closed loops. § Magnetic fields are vector fields, so they have both magnitude and direction. § The unit for magnetic field strength is a Tesla (T). § We use the letter B to represent magnetic field.

Gauss’s Law for Magnetism § Just as we had electric flux, we also have magnetic flux. This represents the number of field lines flowing through a surface. § The unit for magnetic flux is a Webber. § Because magnetic field lines close upon themselves, the total magnetic flux through any closed surface is equal to 0. § Gauss’s Law for magnetism tells us that there are no magnetic monopoles! § There have not been any found in nature, but their existence is a possibility.

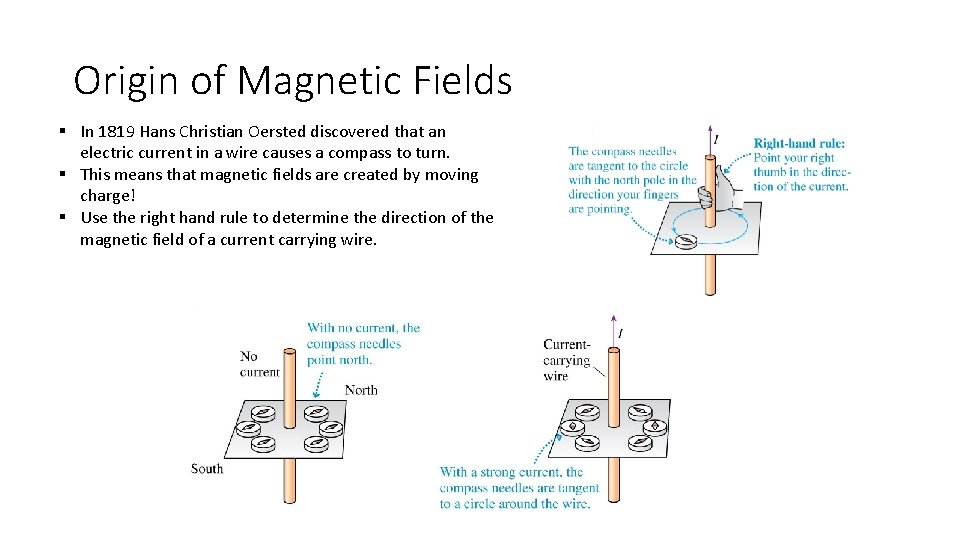
Origin of Magnetic Fields § In 1819 Hans Christian Oersted discovered that an electric current in a wire causes a compass to turn. § This means that magnetic fields are created by moving charge! § Use the right hand rule to determine the direction of the magnetic field of a current carrying wire.

3 Dimensional Vectors § Magnetism requires a three-dimensional perspective, but two-dimensional figures are easier to draw. § We will use the following notation:

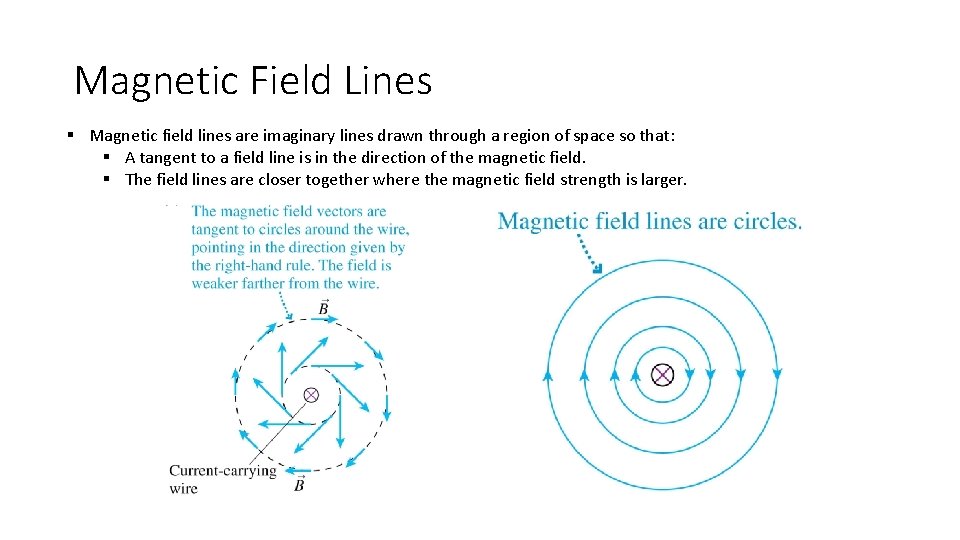
Magnetic Field Lines § Magnetic field lines are imaginary lines drawn through a region of space so that: § A tangent to a field line is in the direction of the magnetic field. § The field lines are closer together where the magnetic field strength is larger.

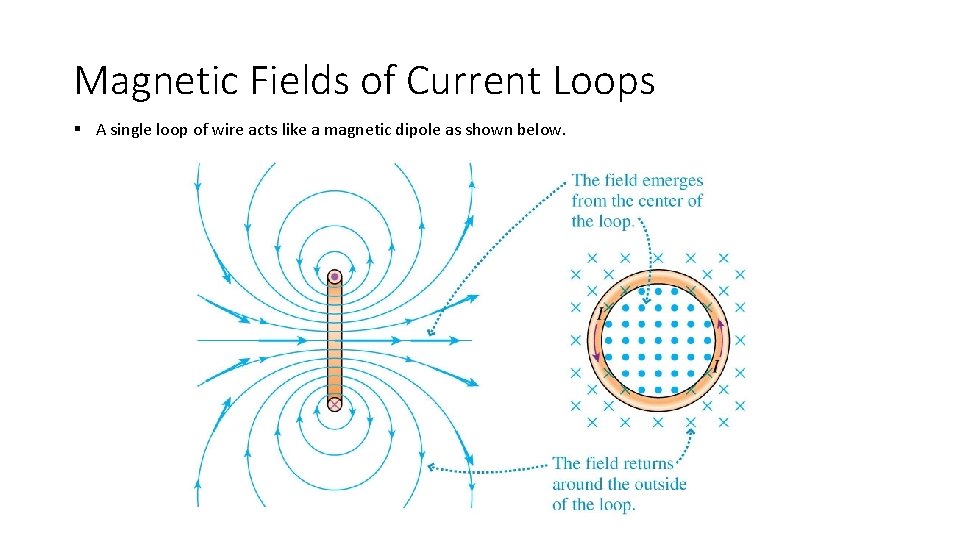
Magnetic Fields of Current Loops § A single loop of wire acts like a magnetic dipole as shown below.

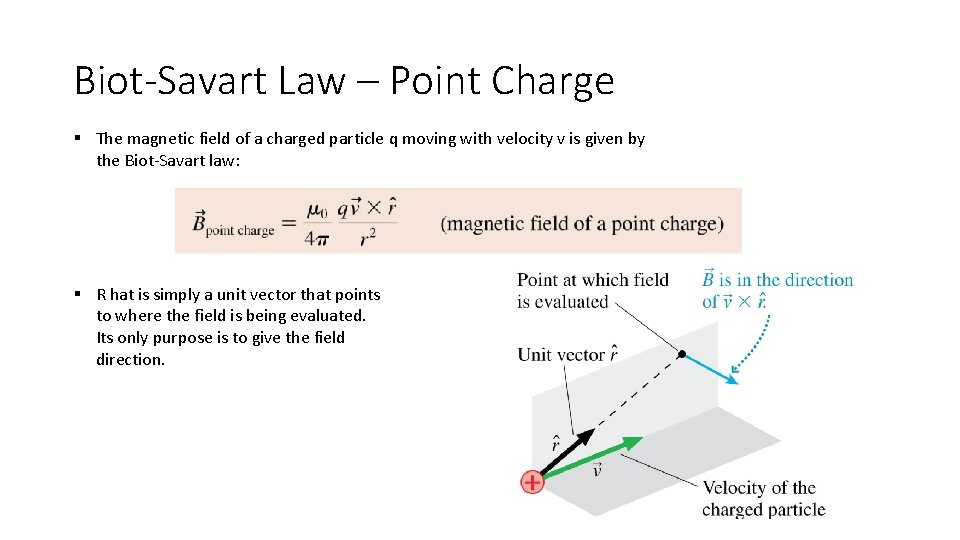
Biot-Savart Law – Point Charge § The magnetic field of a charged particle q moving with velocity v is given by the Biot-Savart law: § R hat is simply a unit vector that points to where the field is being evaluated. Its only purpose is to give the field direction.

Example What is the direction of the magnetic field at the position of the dot? A. Into the screen. B. Out of the screen. C. Up. D. Down. E. Left.

Biot-Savart Law – Current Carrying Wires § Because electric current is the movement of multiple charges, we can use the Biot-Savart Law to calculate the field due to a current carrying wire. § We can express an infinitesimal amount of field due to an infinitesimally small segment of wire: § Because magnetic fields obey the principle of superposition, we can integrate this function to find the total field. § This is generally avoided however, as the geometry involved can be quite difficult.

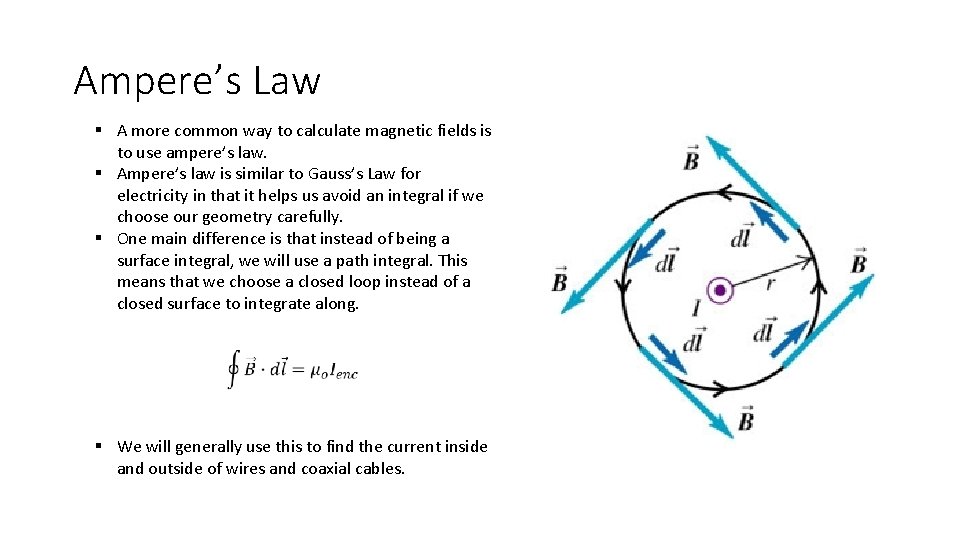
Ampere’s Law § A more common way to calculate magnetic fields is to use ampere’s law. § Ampere’s law is similar to Gauss’s Law for electricity in that it helps us avoid an integral if we choose our geometry carefully. § One main difference is that instead of being a surface integral, we will use a path integral. This means that we choose a closed loop instead of a closed surface to integrate along. § We will generally use this to find the current inside and outside of wires and coaxial cables.

Solenoids § § A uniform magnetic field can be generated with a solenoid. A solenoid is a helical coil of wire with the same current I passing through each loop in the coil. Solenoids may have hundreds or thousands of coils, often called turns, sometimes wrapped in several layers. The magnetic field is strongest and most uniform inside the solenoid.

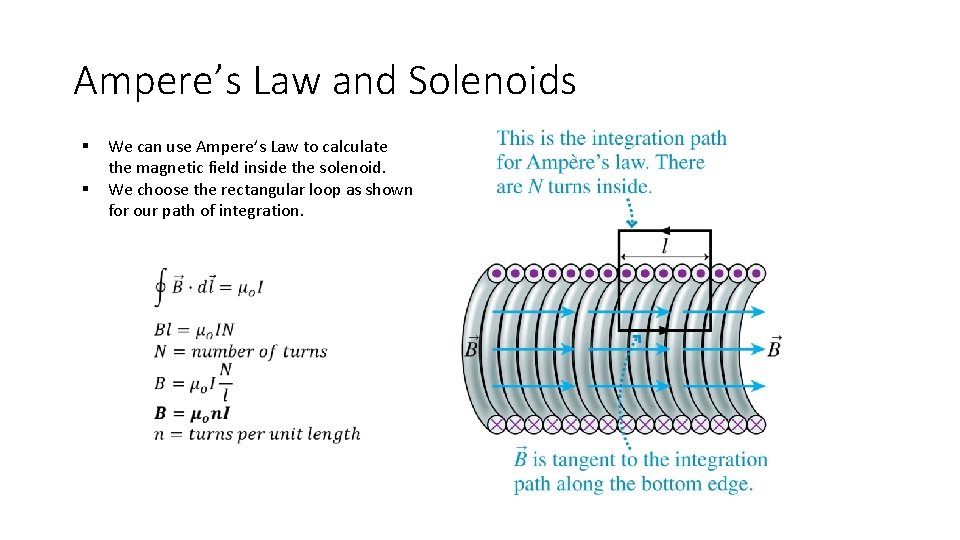
Ampere’s Law and Solenoids § § We can use Ampere’s Law to calculate the magnetic field inside the solenoid. We choose the rectangular loop as shown for our path of integration.

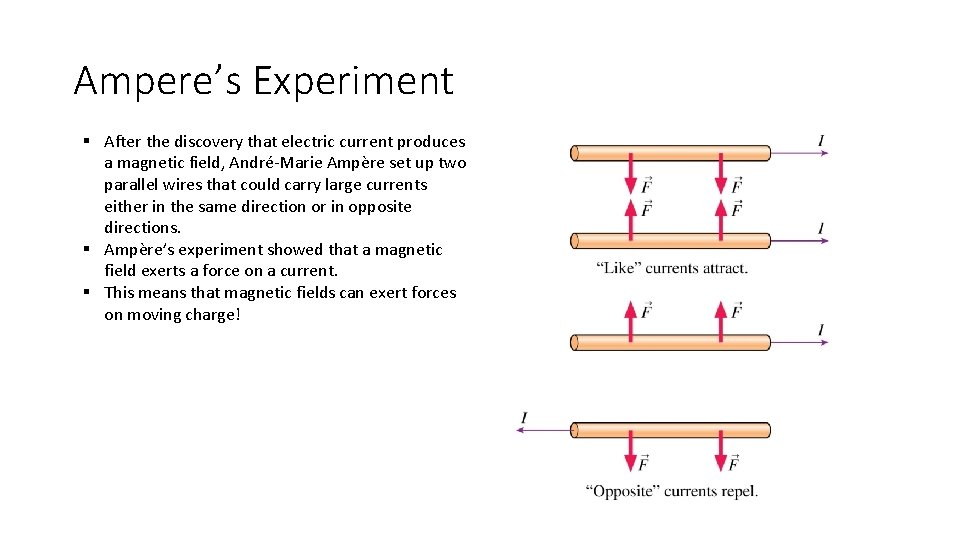
Ampere’s Experiment § After the discovery that electric current produces a magnetic field, André-Marie Ampère set up two parallel wires that could carry large currents either in the same direction or in opposite directions. § Ampère’s experiment showed that a magnetic field exerts a force on a current. § This means that magnetic fields can exert forces on moving charge!

Magnetic Forces § The magnetic force turns out to depend not only on the charge and the charge’s velocity, but also on how the velocity vector is oriented relative to the magnetic field. § We find that the magnetic force on a charged particle moving through a magnetic field is given by:

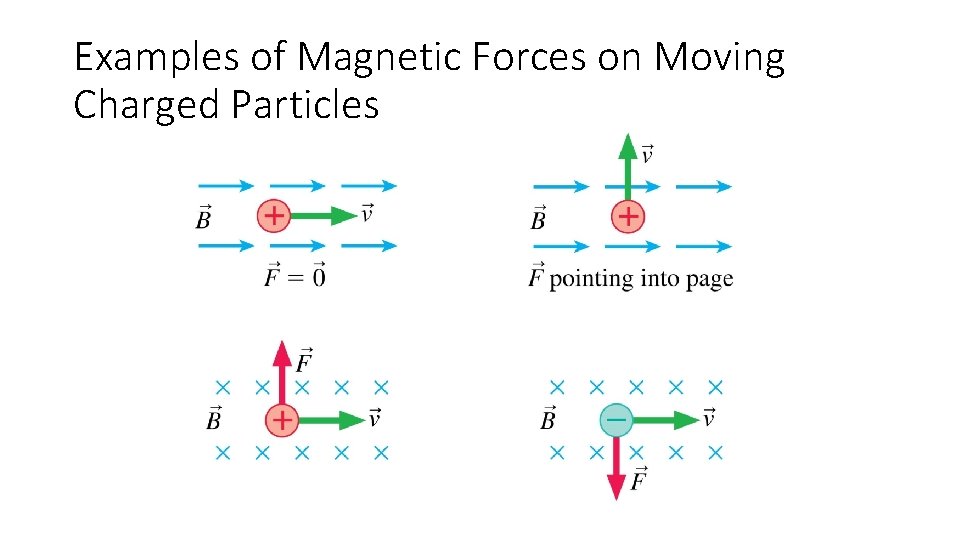
Examples of Magnetic Forces on Moving Charged Particles

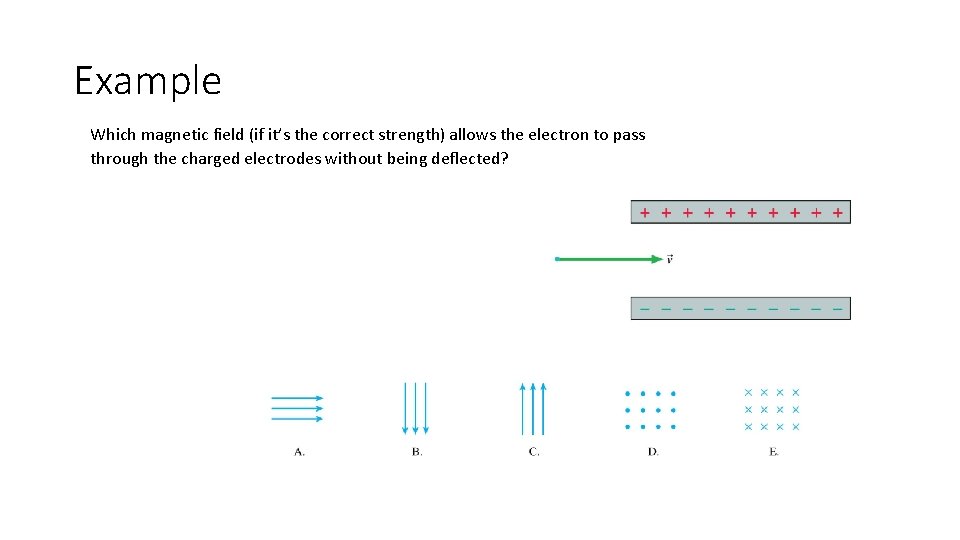
Example Which magnetic field (if it’s the correct strength) allows the electron to pass through the charged electrodes without being deflected?

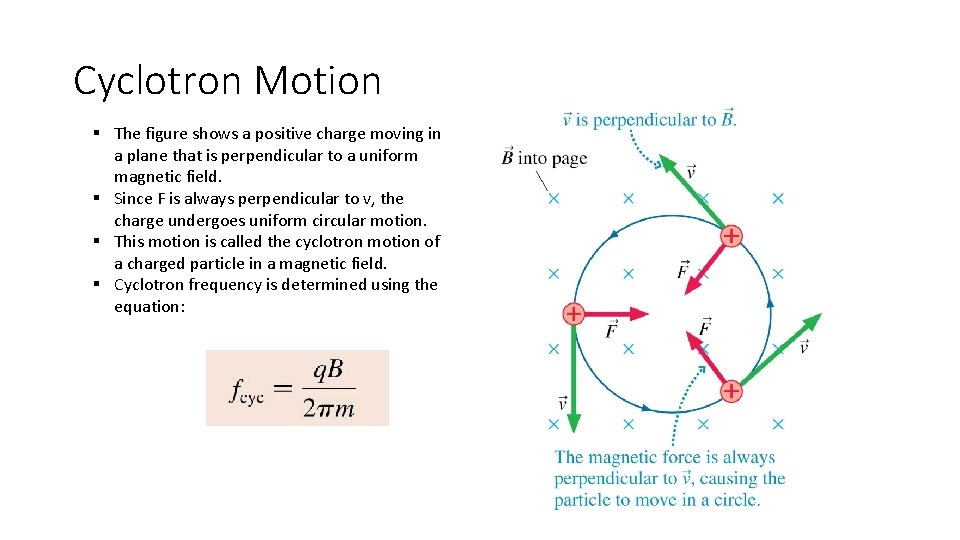
Cyclotron Motion § The figure shows a positive charge moving in a plane that is perpendicular to a uniform magnetic field. § Since F is always perpendicular to v, the charge undergoes uniform circular motion. § This motion is called the cyclotron motion of a charged particle in a magnetic field. § Cyclotron frequency is determined using the equation:

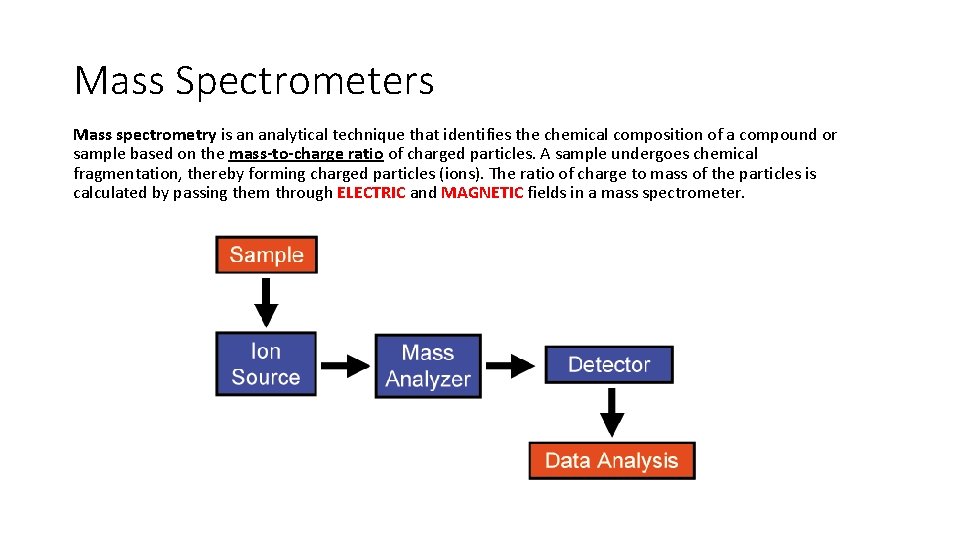
Mass Spectrometers Mass spectrometry is an analytical technique that identifies the chemical composition of a compound or sample based on the mass-to-charge ratio of charged particles. A sample undergoes chemical fragmentation, thereby forming charged particles (ions). The ratio of charge to mass of the particles is calculated by passing them through ELECTRIC and MAGNETIC fields in a mass spectrometer.

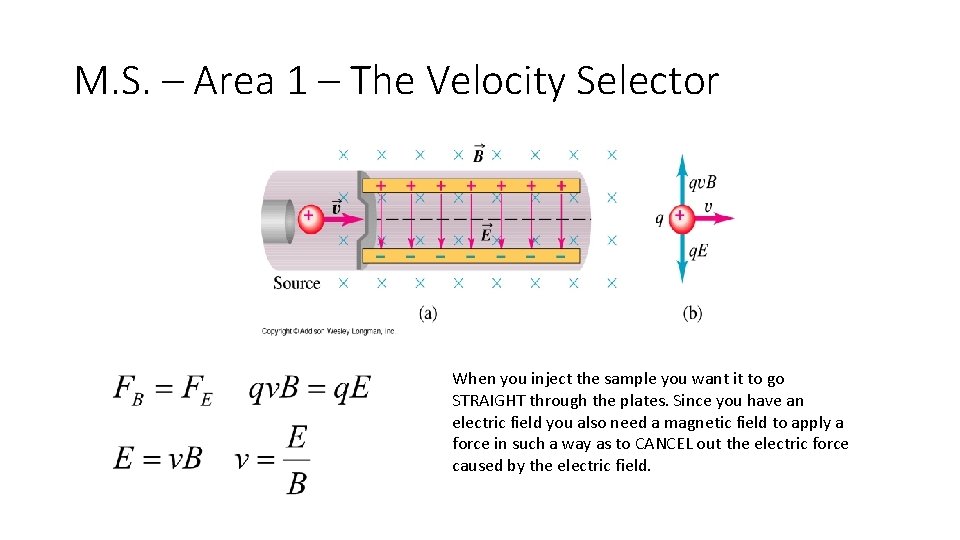
M. S. – Area 1 – The Velocity Selector When you inject the sample you want it to go STRAIGHT through the plates. Since you have an electric field you also need a magnetic field to apply a force in such a way as to CANCEL out the electric force caused by the electric field.

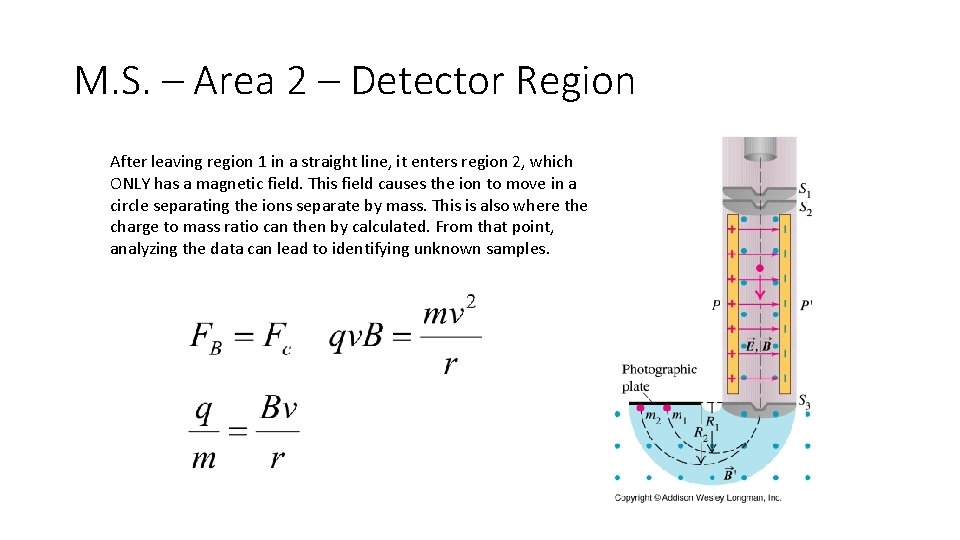
M. S. – Area 2 – Detector Region After leaving region 1 in a straight line, it enters region 2, which ONLY has a magnetic field. This field causes the ion to move in a circle separating the ions separate by mass. This is also where the charge to mass ratio can then by calculated. From that point, analyzing the data can lead to identifying unknown samples.

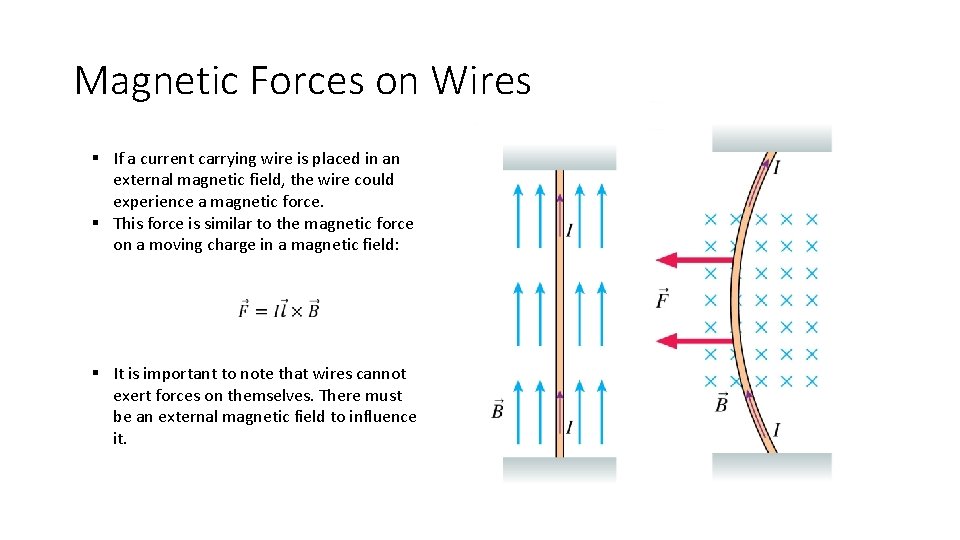
Magnetic Forces on Wires § If a current carrying wire is placed in an external magnetic field, the wire could experience a magnetic force. § This force is similar to the magnetic force on a moving charge in a magnetic field: § It is important to note that wires cannot exert forces on themselves. There must be an external magnetic field to influence it.

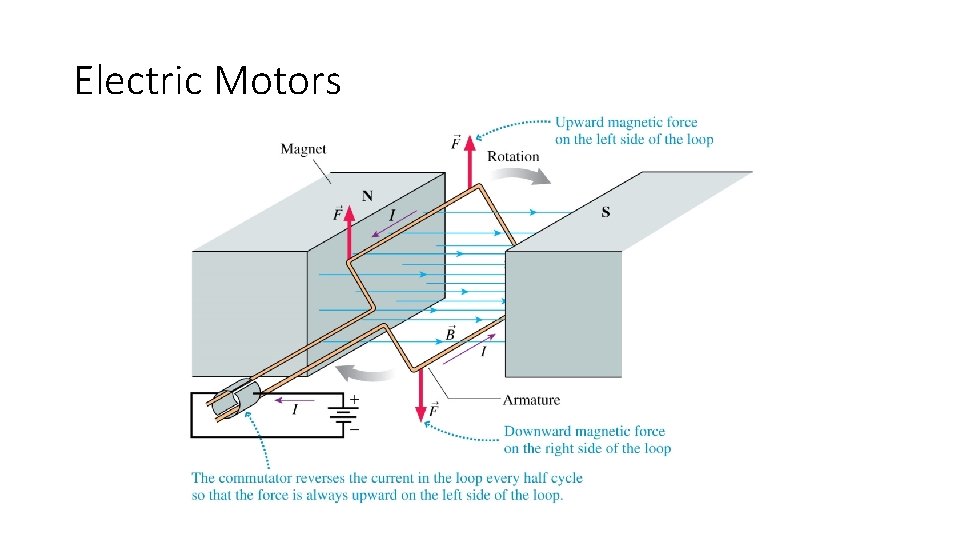
Electric Motors

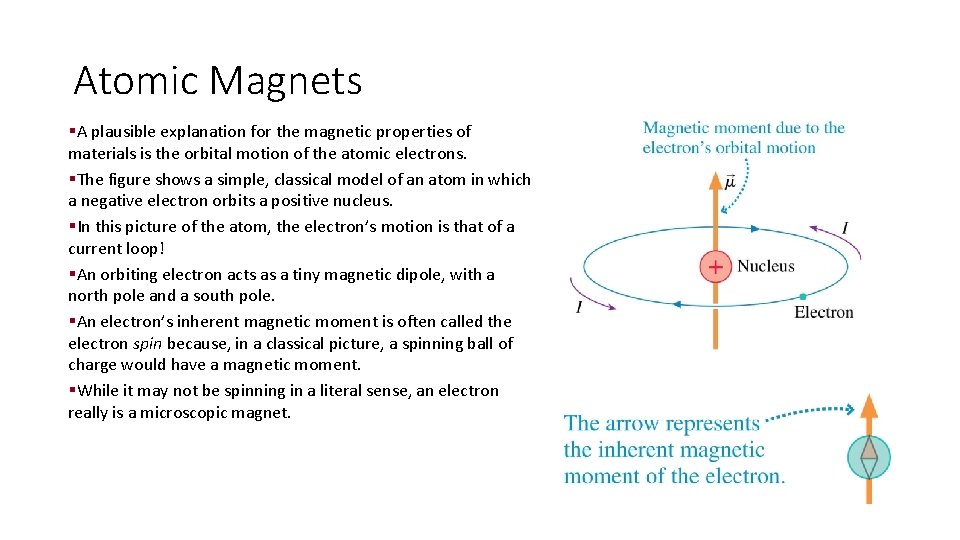
Atomic Magnets §A plausible explanation for the magnetic properties of materials is the orbital motion of the atomic electrons. §The figure shows a simple, classical model of an atom in which a negative electron orbits a positive nucleus. §In this picture of the atom, the electron’s motion is that of a current loop! §An orbiting electron acts as a tiny magnetic dipole, with a north pole and a south pole. §An electron’s inherent magnetic moment is often called the electron spin because, in a classical picture, a spinning ball of charge would have a magnetic moment. §While it may not be spinning in a literal sense, an electron really is a microscopic magnet.

Magnetic Properties of Matter §For most elements, the magnetic moments of the atoms are randomly arranged when the atoms join together to form a solid. §As the figure shows, this random arrangement produces a solid whose net magnetic moment is very close to zero.

Ferromagnetism §In iron, and a few other substances, the atomic magnetic moments tend to all line up in the same direction, as shown in the figure. §Materials that behave in this fashion are called ferromagnetic, with the prefix ferro meaning “iron-like. ” §A typical piece of iron is divided into small regions, typically less than 100 m in size, called magnetic domains. §The magnetic moments of all the iron atoms within each domain are perfectly aligned, so each individual domain is a strong magnet. §However, the various magnetic domains that form a larger solid are randomly arranged.

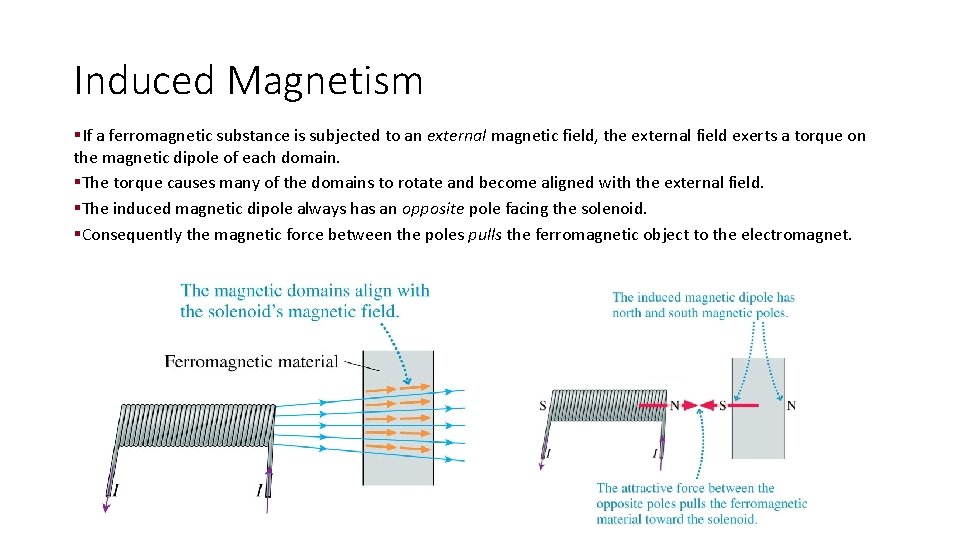
Induced Magnetism §If a ferromagnetic substance is subjected to an external magnetic field, the external field exerts a torque on the magnetic dipole of each domain. §The torque causes many of the domains to rotate and become aligned with the external field. §The induced magnetic dipole always has an opposite pole facing the solenoid. §Consequently the magnetic force between the poles pulls the ferromagnetic object to the electromagnet.