Magnetic Monopoles and the Homotopy Groups Physics 251

Magnetic Monopoles and the Homotopy Groups Physics 251 Jonathan Cornell 6/8/2011

Solitons n n n Finite-energy, non-dissipative solutions of the classical wave equations Cannot arise in linear theories such as electrodynamics, because there is dispersion Non linear theories allow cancelation of dispersive effects

Solitons in Field Theory n M is the set of vacuum field configurations: n Define a topological quantum number πd 2(G/H), where G maps one vacuum to another and H is the isotopy group (G/H is the manifold of the vacuum)

Solitons in 1+1 Dimensions Euler—Lagrange Equations give us the equation of motion This has static solutions at zero and the potential minimum

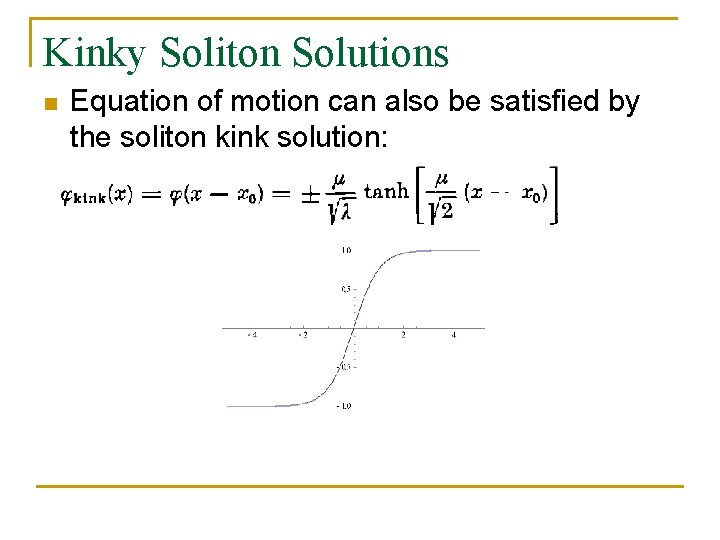
Kinky Soliton Solutions n Equation of motion can also be satisfied by the soliton kink solution:

Topological Charge n The scalar fields in 2 D have a conserved current, leading to a topological charge: n For the kink solution: Charge Topological Quantum Number

Dirac Monopoles n To construct a magnetic monopole, you can have A of the form Magnetic Monopole with charge g

Dirac Quantization Condition n Singularities at θ=0 and θ=π correspond to Dirac string Moving in a circle around string, particle wave function picks up a phase (e-ieg) This phase factor must be equal to 1 for string to be undetectable e-ieg = 1 eg = 2πn

Dirac Quantization Condition n n From previous calculation we see that charge is quantized Monopoles require a compact U(1) gauge group Can be embedded in a larger compact gauge group i. e. SU(2) Also can arise in Kaluza-Klein theories

Soliton in 2+1 Dimensions (Nielsen. Olsen Model) n n n Here Dμ=∂μ – ie. Aμ and Φ is a complex valued field Vacuum is identified with Fμν=0, Dμϕ=0, The vacuum fields have the values

Boundary Conditions n As r→∞, we need to have vacuum states. Working in gauge where A 0=0 and considering the requirements on vacuum solution: n Defining χ(θ)=nθ where refers to a homotopy class we find that magnetic field through (x, y) plane is quantized.

‘t Hooft-Polyakov Model (3+1 dimensions) n Φa are scalar fields in the adjoint representation of SU(2) (a=1, 2, 3). n The vacuum state manifold is a 2 sphere with radius n

Boundary Conditions n r→∞, need vacuum state, Dμϕa=0 n Shown by ‘t Hooft that Wμa and Fμν are related by (Φ={ϕa}): n Working out electric and magnetic fields using the r→∞ limit value of Wμa

Quantization of Magnetic Charge n n n This is same as Dirac quantization condition (eg = 2πn) with n = 2! Considering all possible solutions of the equations of motion for this theory, it can be shown we get the Dirac quantization condition with n even Agrees with result for possible homotopy classes

Mass of Monopoles n n n t’ Hooft showed , where MV is gauge boson mass Monopoles arise in GUTs, with mass of the scale of the symmetry breaking of theory SU(5): GUT monopoles are too massive to be produced in accelerators, but could have been produced in early universe Monopole searches focus on accelerators, cosmic rays, and on monopoles possibly bound in matter To date, nothing found

References n n n Boya L. et al. “Homotopy and Solitons. ” Fortschritte der Physik 26, 175 -214 (1978). Coleman, S. “Magnetic Monopole Fifty Years Later. ” from The Unity of the Fundamental Interactions, A. Zichichi, ed. European Physical Society, 1981. Dine, Michael. Supersymmetry and String Theory. Cambridge University Press, 2007. Goddard P. and D. I. Olive, “Magnetic monopoles in gauge field theories. ” Rep. Prog. Phys. , 41, 1357 -1437 (1978). Harvey, Jeffrey A. “Magnetic Monopoles, Duality, and Supersymmetry. ” ar. Xiv: hep-th/9603086 Milstead, D. and E. J. Weinberg. “Magnetic Monopoles. ” from K. Nakamura et al. (Particle Data Group), JPG 37, 075021 (2010).