Magini kvadrat l lo shu LO SHU 4

Magični kvadrat l lo shu

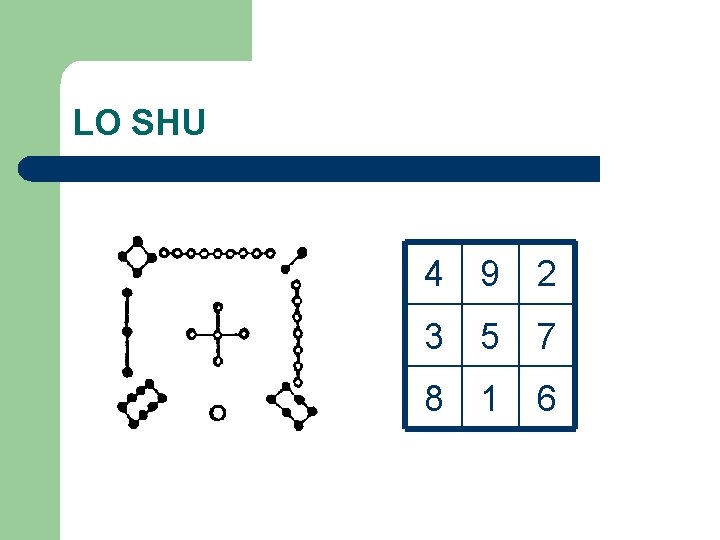
LO SHU 4 9 2 3 5 7 8 1 6

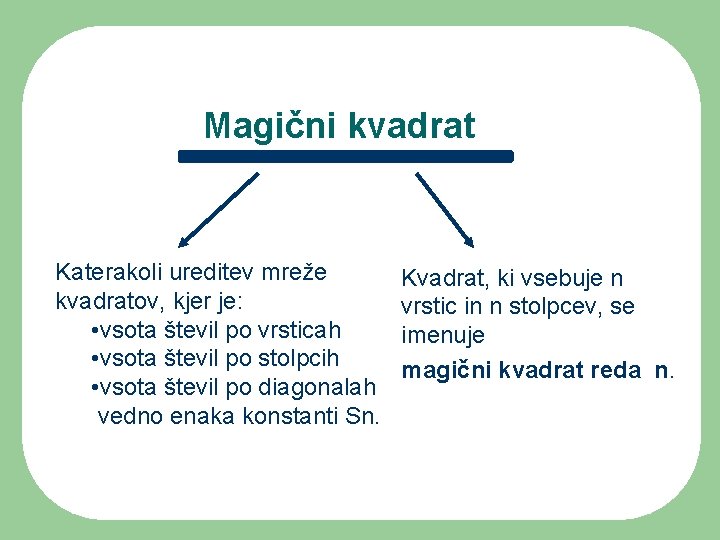
Magični kvadrat Katerakoli ureditev mreže kvadratov, kjer je: • vsota števil po vrsticah • vsota števil po stolpcih • vsota števil po diagonalah vedno enaka konstanti Sn. Kvadrat, ki vsebuje n vrstic in n stolpcev, se imenuje magični kvadrat reda n.

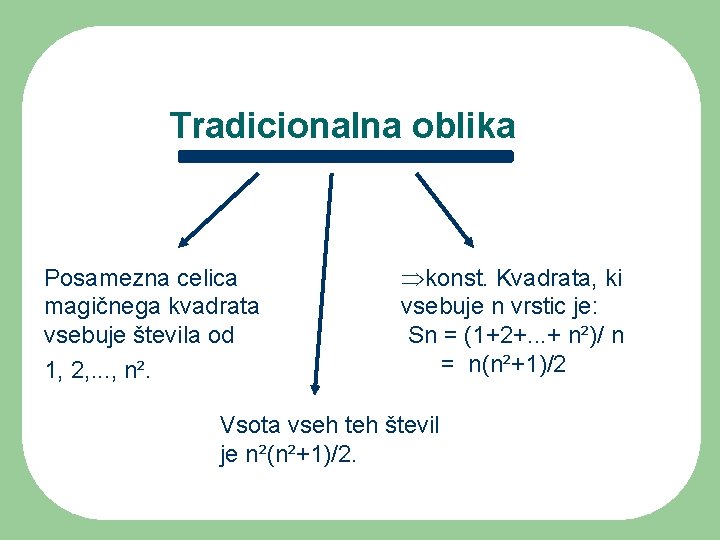
Tradicionalna oblika Posamezna celica magičnega kvadrata vsebuje števila od 1, 2, . . . , n². konst. Kvadrata, ki vsebuje n vrstic je: Sn = (1+2+. . . + n²)/ n = n(n²+1)/2 Vsota vseh teh števil je n²(n²+1)/2.

METODA OKVIRJANJA Az-Zinjani (13. stoletje) l l Metoda deluje na kvadratih lihega reda. Kvadrat gradimo od zunanjega okvirja proti notranjemu. 1. okvir 2. okvir 3. okvir

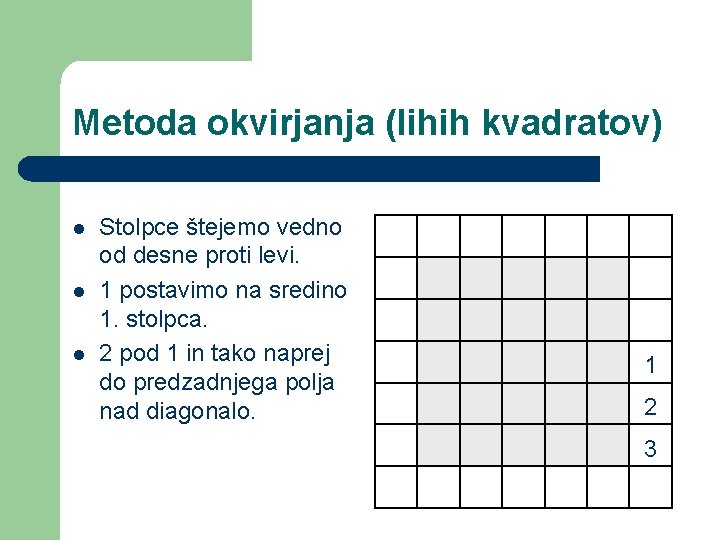
Metoda okvirjanja (lihih kvadratov) l l l Stolpce štejemo vedno od desne proti levi. 1 postavimo na sredino 1. stolpca. 2 pod 1 in tako naprej do predzadnjega polja nad diagonalo. 1 2 3

Metoda okvirjanja (lihih kvadratov) l l V zadnji stolpec in zadnjo vrstico zapišemo naslednika prejšnjega. Nadaljujemo z zapisom naslednikov v vsa polja do srednjega stolpca, ki ostane prazen. 1 2 3 6 4 5

Metoda okvirjanja (lihih kvadratov) l V srednje polje 1. vrstice zapišemo naslednje število. 7 1 2 3 6 4 5

Metoda okvirjanja (lihih kvadratov) l l Premaknemo se v polje zadnjega (skrajno levega) stolpca nad vrstico v sredini. Nadaljujemo z zapisom števil po stolpcu navzgor. 10 7 9 8 1 2 3 6 4 5

Metoda okvirjanja (lihih kvadratov) l Nadalje vpišemo števila v polja med srednjim in prvim (skrajno desnim) poljem prve vrstice. 10 9 8 1 2 3 6 4 5 7 11 12

Metoda okvirjanja (lihih kvadratov) l l Pri konstruiranju kvadrata reda n, dopolnimo ostala polja okvirja tako, da bo vsota medsebojno nasproti ležečih polj = n²+1. Poljema v kotih predpišemo polji v nasprotnem kotu kvadrata. 10 45 44 7 11 12 46 9 41 8 42 49 1 48 2 47 3 4 5 6 43 39 38 40

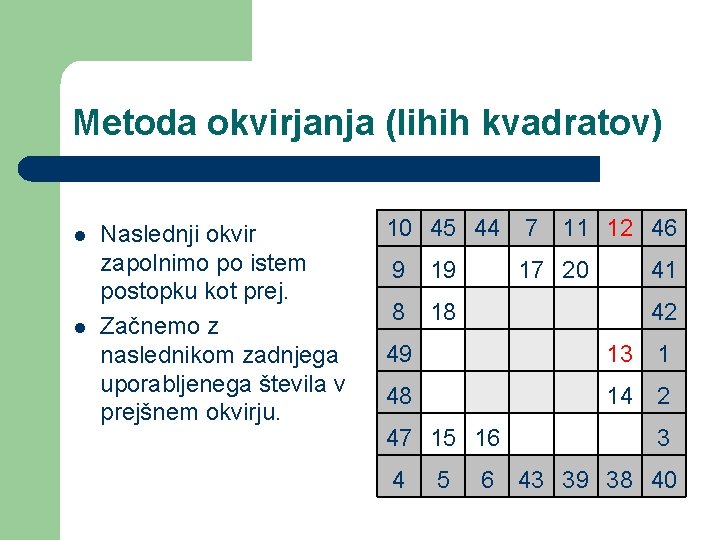
Metoda okvirjanja (lihih kvadratov) l l Naslednji okvir zapolnimo po istem postopku kot prej. Začnemo z naslednikom zadnjega uporabljenega števila v prejšnem okvirju. 10 45 44 7 9 19 17 20 8 18 49 48 47 15 16 4 5 6 11 12 46 41 42 13 1 14 2 3 43 39 38 40

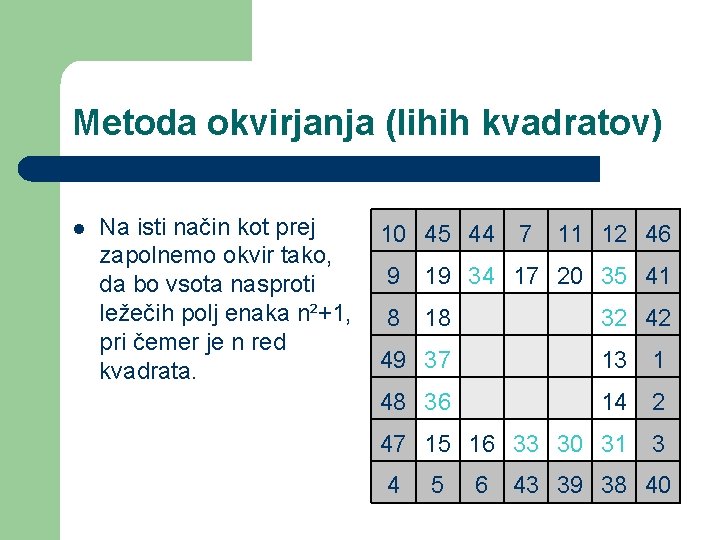
Metoda okvirjanja (lihih kvadratov) l Na isti način kot prej 10 45 44 7 11 12 46 zapolnemo okvir tako, 9 19 34 17 20 35 41 da bo vsota nasproti ležečih polj enaka n²+1, 8 18 32 42 pri čemer je n red 49 37 13 1 kvadrata. 48 36 14 2 47 15 16 33 30 31 4 5 6 3 43 39 38 40

Metoda okvirjanja (lihih kvadratov) l l Enako nadaljujemo v naslednjem okviru in tako vse do zadnjega, ki vsebuje samo še eno prosto polje. V to polje zapišemo naslednika števila pri katerem smo končali šteti v predzadnjem okviru. 10 45 44 7 11 12 46 9 19 34 17 20 35 41 8 18 24 23 28 32 42 49 37 29 25 21 13 1 48 36 22 27 26 14 2 47 15 16 33 30 31 3 4 5 6 43 39 38 40

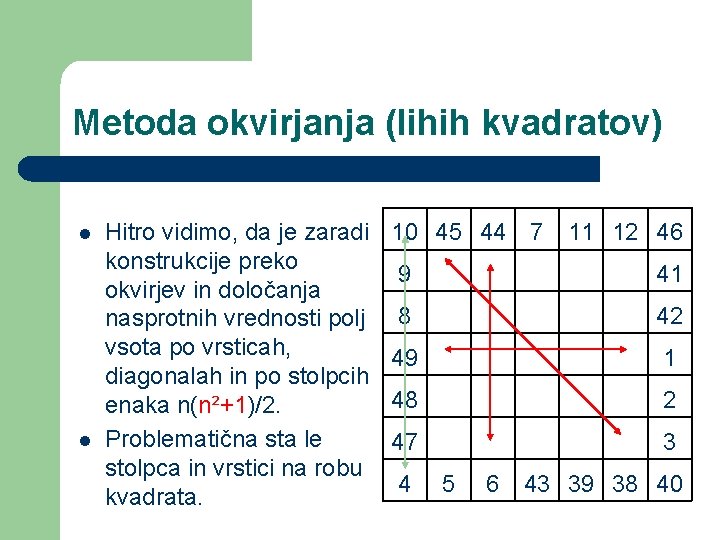
Metoda okvirjanja (lihih kvadratov) l l Hitro vidimo, da je zaradi konstrukcije preko okvirjev in določanja nasprotnih vrednosti polj vsota po vrsticah, diagonalah in po stolpcih enaka n(n²+1)/2. Problematična sta le stolpca in vrstici na robu kvadrata. 10 45 44 7 11 12 46 9 41 8 42 49 1 48 2 47 3 4 5 6 43 39 38 40

Metoda okvirjanja (lihih kvadratov) NAMIG: (n=2 k+1) 3 k+1 2 k+1 3 k+2 . . . 4 k . . . 2 k+2 n² 1 . . . n²-k+1 k k+1 . . . 2 k n²-2 k

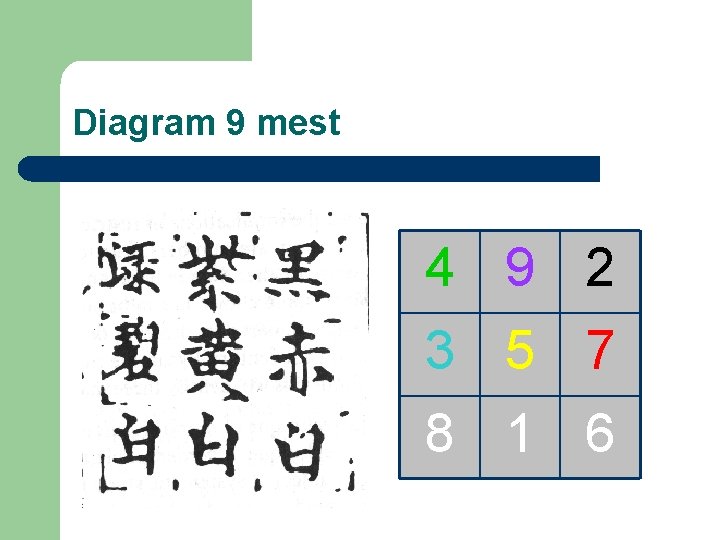
Diagram 9 mest 4 9 2 3 5 7 8 1 6

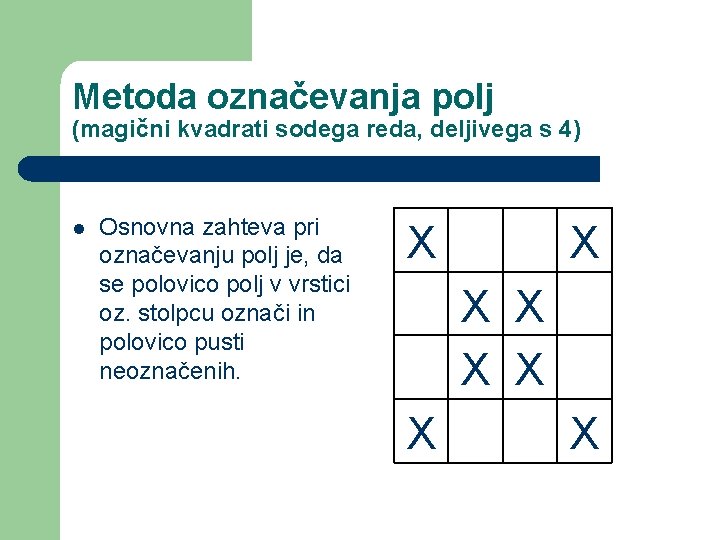
Metoda označevanja polj (magični kvadrati sodega reda, deljivega s 4) l Osnovna zahteva pri označevanju polj je, da se polovico polj v vrstici oz. stolpcu označi in polovico pusti neoznačenih. X X X X

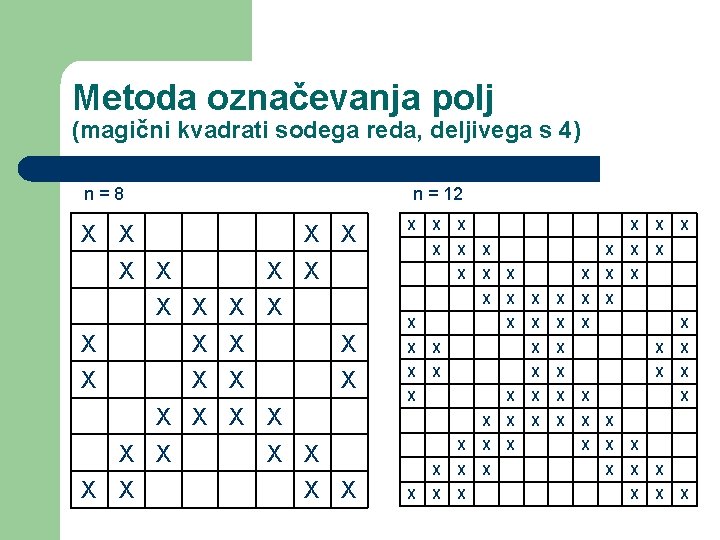
Metoda označevanja polj (magični kvadrati sodega reda, deljivega s 4) n = 8 X X n = 12 X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X

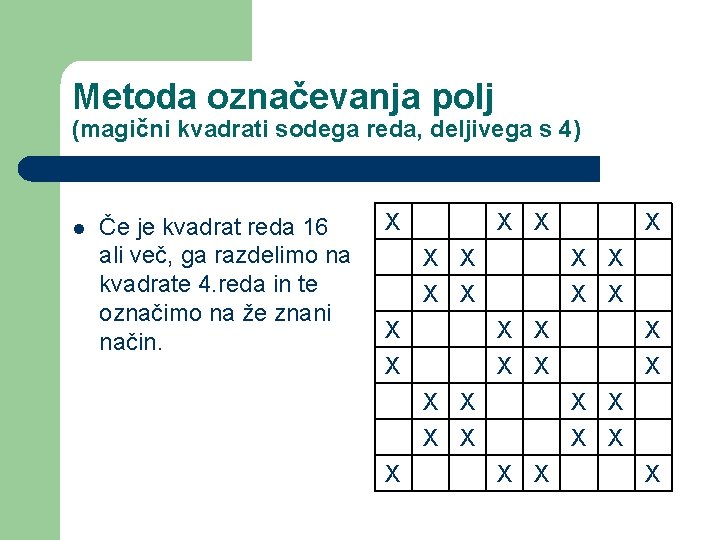
Metoda označevanja polj (magični kvadrati sodega reda, deljivega s 4) l Če je kvadrat reda 16 ali več, ga razdelimo na kvadrate 4. reda in te označimo na že znani način. X X X X X X X X

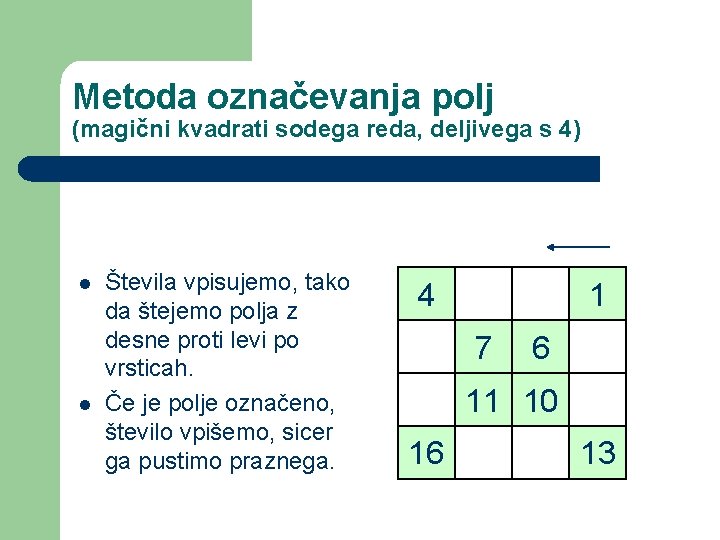
Metoda označevanja polj (magični kvadrati sodega reda, deljivega s 4) l l Števila vpisujemo, tako da štejemo polja z desne proti levi po vrsticah. Če je polje označeno, število vpišemo, sicer ga pustimo praznega. 4 16 7 11 6 10 1 13

Metoda označevanja polj (magični kvadrati sodega reda, deljivega s 4) l Kvadrat dopolnimo na enak način s štetjem, le da začnemo šteti skrajno levo v zadnji vrstici in zapolnjujemo le polja, ki so ostala prazna. 4 14 15 1 9 7 6 12 5 11 10 8 16 2 13 3

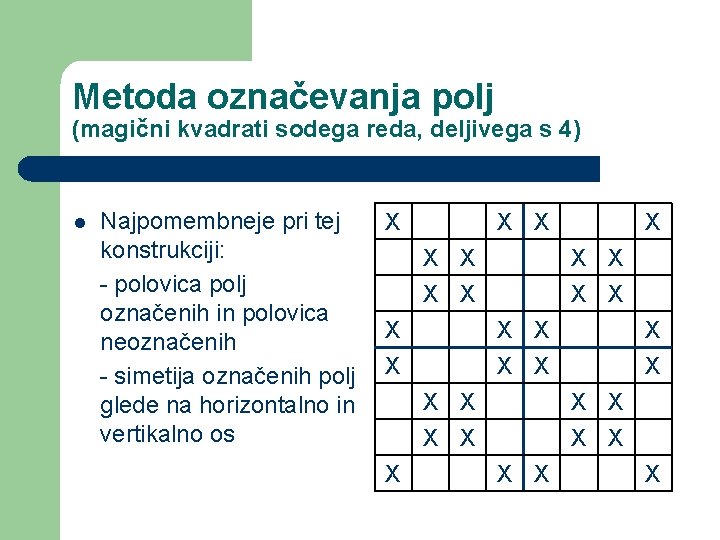
Metoda označevanja polj (magični kvadrati sodega reda, deljivega s 4) Najpomembneje pri tej X X X konstrukciji: X X - polovica polj X X označenih in polovica X X X neoznačenih - simetija označenih polj X X X glede na horizontalno in X X vertikalno os X X X X l X X

Metoda označevanja polj (magični kvadrati sodega reda, deljivega s 4) c-ti stolpec NAMIG: . . . 2. 1. v-ta vrstica n(n-v)+nc+1 p-ta vrstica n(p-1)+c . . . q-ta vrstica n(q-1)+c u-ta vrstica n(n-u)+nc+1 p+q = n+1 u+v = n+1

Dürer-jeva Melanholija 1 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1

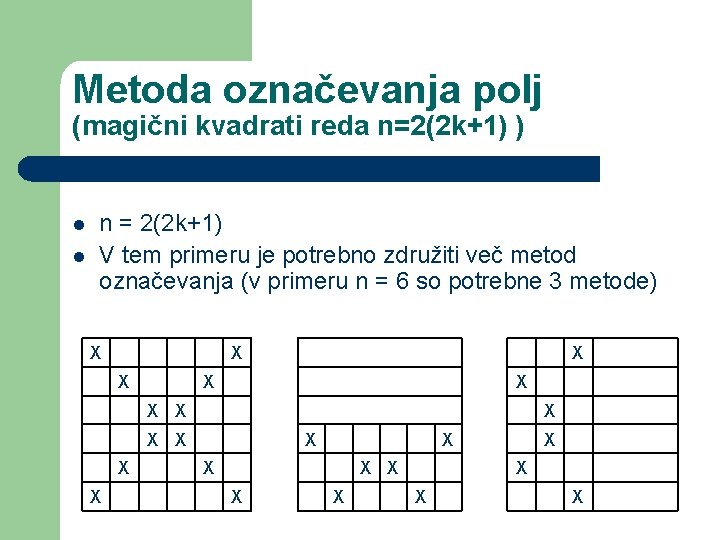
Metoda označevanja polj (magični kvadrati reda n=2(2 k+1) ) n = 2(2 k+1) V tem primeru je potrebno združiti več metod označevanja (v primeru n = 6 so potrebne 3 metode) l l X X X X X X X X X X X X X

Metoda označevanja polj (magični kvadrati reda n=2(2 k+1) ) 3. 1. 6 32 3 34 35 1 7 11 27 28 8 30 19 14 16 15 23 24 18 20 22 21 17 13 25 29 10 9 26 12 36 5 33 4 2 31 4. 2.

Železna spominska plošča

1. A History of Algorithms, avtor: Jean-Luc Chabert 2. http: //illuminations. nctm. org/Lesson. Detail. aspx? id=L 263 HVALA!