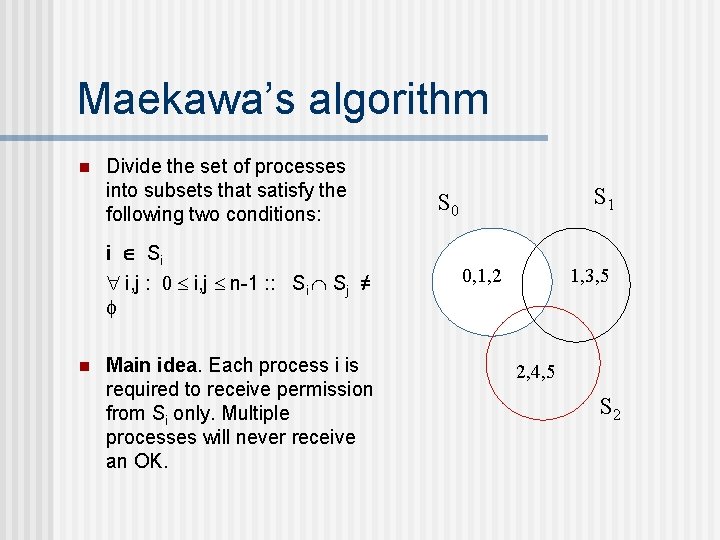
Maekawas algorithm n Divide the set of processes

Maekawa’s algorithm n Divide the set of processes into subsets that satisfy the following two conditions: i Si i, j : i, j n-1 : : Si Sj ≠ n Main idea. Each process i is required to receive permission from Si only. Multiple processes will never receive an OK. S 1 S 0 0, 1, 2 1, 3, 5 2, 4, 5 S 2

Maekawa’s algorithm Example. Let there be seven processes 0, 1, 2, 3, 4, 5, 6 S 0 S 1 S 2 S 3 S 4 S 5 S 6 = = = = {0, 1, 2} {1, 3, 5} {2, 4, 5} {0, 3, 4} {1, 4, 6} {0, 5, 6} {2, 3, 6}

Maekawa’s algorithm Version 1 {Life of process I} S 0 = {0, 1, 2} 1. Send timestamped request to each process in Si. S 1 = {1, 3, 5} S 2 = {2, 4, 5} 2. Request received send ack to process with the lowest timestamp. Thereafter, "lock" (i. e. commit) yourself to that process, and keep others waiting. S 3 = {0, 3, 4} S 4 = {1, 4, 6} S 5 = {0, 5, 6} S 6 = {2, 3, 6} 3. Enter CS if you receive ack from each member in Si. 4. To exit CS, send release to every process in Si.

Maekawa’s algorithm Proof of ME 1. At most one process can enter its critical section at any time. Let i and j attempt to enter their Critical Sections Si � Sj ≠ �there is a process k Si � Sj Process k will not send ack to both. So it will act as the arbitrator. S 0 = {0, 1, 2} S 1 = {1, 3, 5} S 2 = {2, 4, 5} S 3 = {0, 3, 4} S 4 = {1, 4, 6} S 5 = {0, 5, 6} S 6 = {2, 3, 6}

Maekawa’s algorithm Proof of ME 2. No deadlock S 0 = {0, 1, 2} Unfortunately deadlock is possible! S 1 = {1, 3, 5} S 2 = {2, 4, 5} S 3 = {0, 3, 4} S 4 = {1, 4, 6} ack to 2; S 5 = {0, 5, 6} Prom S 2={2, 4, 5}, 4, 5 send ack to 2, but 2 sends S 6 = {2, 3, 6} n From S 0={0, 1, 2}, 0, 2 send ack to 0, but 1 sends ack to 1; n n From S 1={1, 3, 5}, 1, 3 send ack to 1, but 5 sends ack to 0; Now, 0 waits for 1, 1 waits for 2, and 2 waits for 0. So deadlock is possible!

Maekawa’s algorithm-Version 2 Avoiding deadlock If processes could receive messages in increasing order of timestamp, then deadlock “could be” avoided. But this is too strong an assumption. So version 2 uses three more messages: - failed - inquire - relinquish S 0 = {0, 1, 2} S 1 = {1, 3, 5} S 2 = {2, 4, 5} S 3 = {0, 3, 4} S 4 = {1, 4, 6} S 5 = {0, 5, 6} S 6 = {2, 3, 6}

Maekawa’s algorithm-Version 2 What is new in version 2? Send ack and set lock as usual. If lock is set and a request with larger timestamp arrives, send failed (you have no chance). If the incoming request has a lower timestamp, then send inquire (are you in CS? ) to the locked process. Receive inquire and at least one failed message send relinquish. The recipient resets the lock. S 0 = {0, 1, 2} S 1 = {1, 3, 5} S 2 = {2, 4, 5} S 3 = {0, 3, 4} S 4 = {1, 4, 6} S 5 = {0, 5, 6} S 6 = {2, 3, 6}

Maekawa’s algorithm-Version 2 Example

Comments n Let K = |Si|. Let each process be a member of D subsets. When N = 7, K = D = 3. When K=D, N = K(K-1)+1. So K is of the order √N n The message complexity of Version 1 is 3√N. Maekawa’s analysis of Version 2 reveals a complexity of 7√N

Token-passing Algorithms Suzuki-Kasami algorithm n Completely connected network of processes n There is one token in the network. The owner of the token has the permission to enter CS. n Token will pass from one process to another based on demand.

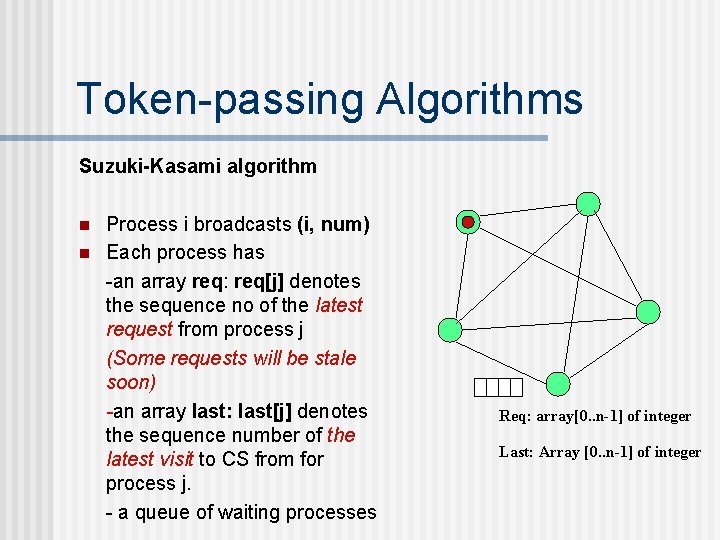
Token-passing Algorithms Suzuki-Kasami algorithm n n Process i broadcasts (i, num) Each process has -an array req: req[j] denotes the sequence no of the latest request from process j (Some requests will be stale soon) -an array last: last[j] denotes the sequence number of the latest visit to CS from for process j. - a queue of waiting processes Req: array[0. . n-1] of integer Last: Array [0. . n-1] of integer

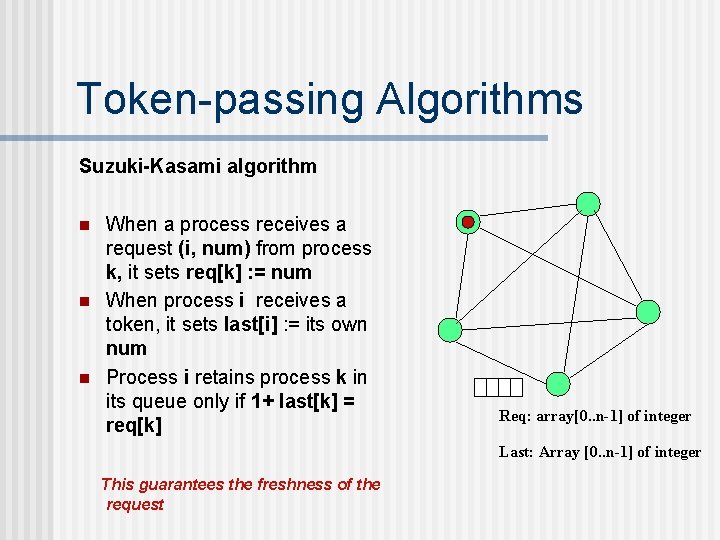
Token-passing Algorithms Suzuki-Kasami algorithm n n n When a process receives a request (i, num) from process k, it sets req[k] : = num When process i receives a token, it sets last[i] : = its own num Process i retains process k in its queue only if 1+ last[k] = req[k] Req: array[0. . n-1] of integer Last: Array [0. . n-1] of integer This guarantees the freshness of the request

Shared-memory algorithms for mutex Complexity of the solution depends on the grain of atomicity. - Atomic reads and writes (what does it mean? ) (Numerous solutions have been proposed) - Using read-modify-writes (what is this? ) (Somewhat simpler to use) - Using LL (Load Linked) and SC (Store Conditional) primitives (Easy to use, but somewhat unconventional)

Solution using atomic read/write define turn 0, turn 1 : shared Boolean (initially false} {process 0} do true turn 0 : = true; do turn 1 skip od; Critical Section; turn 0: = false; od What is the problem here? {process 1} do true turn 1: =true; do turn 0 skip od; Critical Section; turn 1: = false; od

Peterson’s two-process algorithm program peterson; Define flag[0], flag[1]: shared boolean {initially false} turn: shared integer {initially 0} {Program for process 0} do 1: 2: 3: od 4: 5: 6: od true flag[0] = true; turn = 0; do (flag[1] turn =0) skip critical section; flag[0] = false; non-critical section codes; {Program for process 1} do 7: 8: 9: od; 10: 11: 12: od true flag[1] = true; turn = 1; do (flag[0] turn = 1) skip critical section; flag[1] = false; non-critical section codes;

Does it work? ME 1. At most one process in CS Let 0 be in CS. Can 1 enter its CS? Let’s see … 0 in CS flag[1] = false OR turn = 1 OR both. To enter CS, 1 must see flag[0] = false OR turn = 0 OR both. But 0 in CS flag[0] = true! So turn =0 should hold.

Does it work? Case 1. process 0 reads flag[1] = false in step 3 process 1 has not executed step 7 process 1 eventually sets turn to 1 (step 8) process 1 checks turn (step 9) and finds turn =1 process 1 waits in step 9 and cannot enter its CS

Does it work? Case 2. process 0 reads turn = 1 in step 3 process 1 executed step 8 after 0 executed step 2 in step 9 process 1 reads flag[0] = true and turn = 1 process 1 waits in step 9 and cannot enter its CS

Does it work? ME 2. No deadlock (flag[1] turn =0) (flag[0] turn = 1) = false

Does it work? ME 3. Progress (eventual entry into CS) Argue about this yourself.