MAE 430 Introduction to Reliability in Mechanical Engineering

MAE 430 Introduction to Reliability in Mechanical Engineering Design Project 2 : Evaluation of Reliability in S-S Model 20090021 Wonseok Kang 20090848 Dongha Chung

TABLE OF CONTENTS Process of Analysis Determination of Stress and Strength Model Calculation Method Case 1 : Given Probability Density Function Case 2 : Given Data Our Results Case 1 : Given Probability Density Function Case 2 : Given Data Comparison of Both Results Conclusion

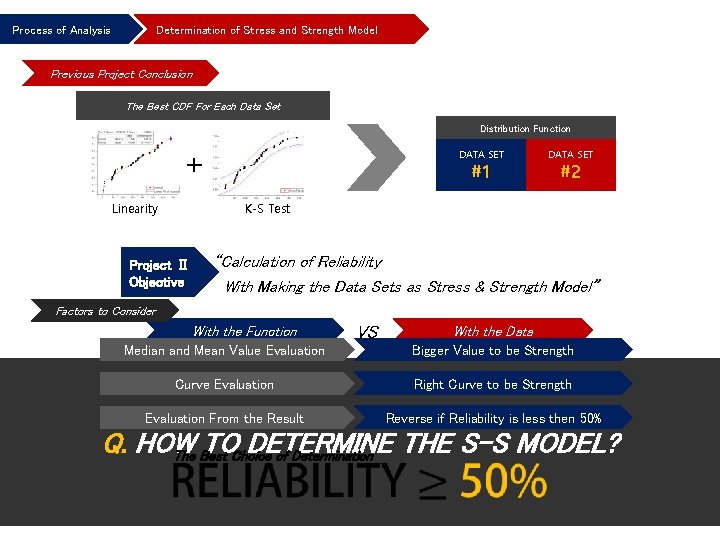
Process of Analysis Determination of Stress and Strength Model Previous Project Conclusion The Best CDF For Each Data Set Distribution Function + Linearity DATA SET #1 DATA SET #2 K-S Test Project Ⅱ Objective “Calculation of Reliability With Making the Data Sets as Stress & Strength Model” Factors to Consider With the Function VS With the Data Median and Mean Value Evaluation Bigger Value to be Strength Curve Evaluation Right Curve to be Strength Evaluation From the Result Reverse if Reliability is less then 50% Q. HOW TO DETERMINE THE S-S MODEL? The Best Choice of Determination

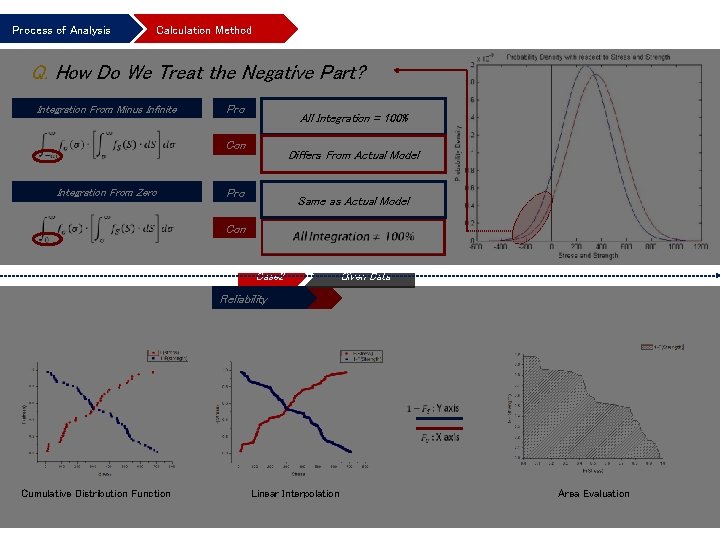
Process of Analysis Calculation Method Q. How Do We Treat the Negative Part? Integration From Minus Infinite From Equation (9. 1 -1) Pro All Integration = 100% Con Integration From Zero Normal Distribution Differs From Actual Model Pro Same as Actual Model Log. Normal Distribution Con Weibull Distribution Case 1 Given Probability Density Function Case 2 Given Data Bi-Exponential Distribution Reliability Failure Probability ~~ ~~ ~~ Cumulative Distribution Function Lower Limit of Failure Probability Symmetric Simple CDF Linear Interpolation Probability Mean Rank Triangular Method of Failure Median Rank Method Area Evaluation Areaof. Evaluation Upper Limit Failure. Method Probability Other

n tio nc 1 Fu e y t as nsi C ility De b a rob G P n e iv

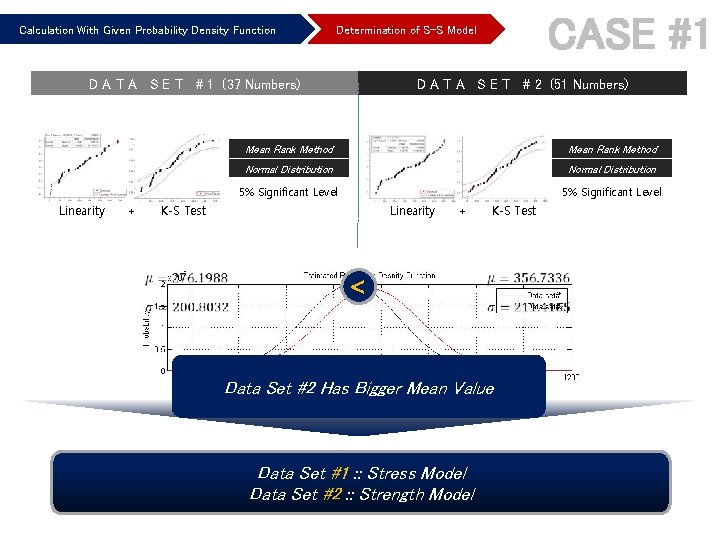
Calculation With Given Probability Density Function D A T A S E T # 1 (37 Numbers) Linearity + CASE #1 Determination of S-S Model D A T A S E T # 2 (51 Numbers) Mean Rank Method Normal Distribution 5% Significant Level K-S Test Linearity + K-S Test < Data Set #2 Has Bigger Mean Value Data Set #1 : : Stress Model Data Set #2 : : Strength Model

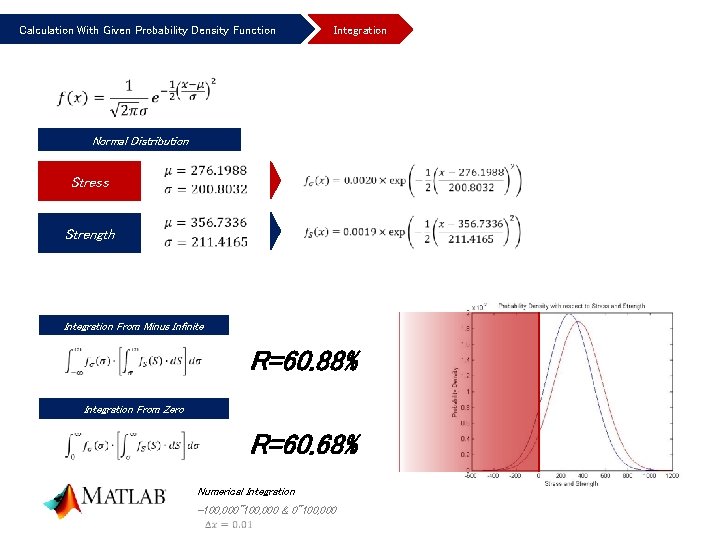
Calculation With Given Probability Density Function Integration Normal Distribution Stress Strength Integration From Minus Infinite R=60. 88% Integration From Zero R=60. 68% Numerical Integration -100, 000~100, 000 & 0~100, 000

2 e as ta C iven Da G

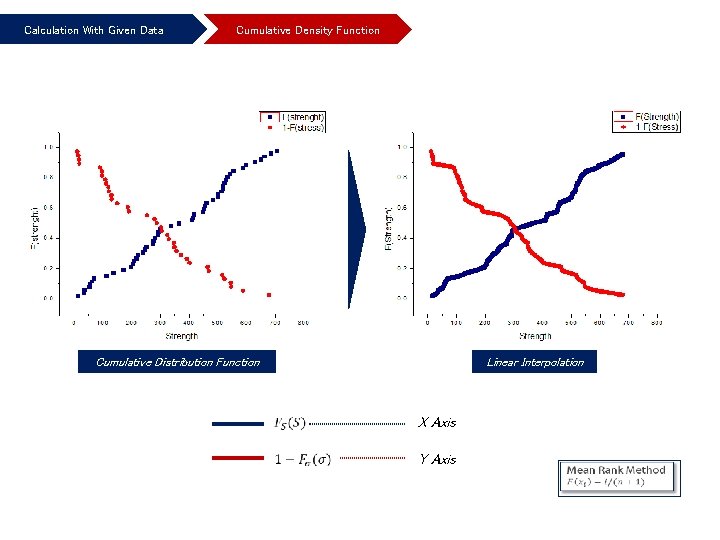
Calculation With Given Data Cumulative Density Function Cumulative Distribution Function Linear Interpolation X Axis Y Axis

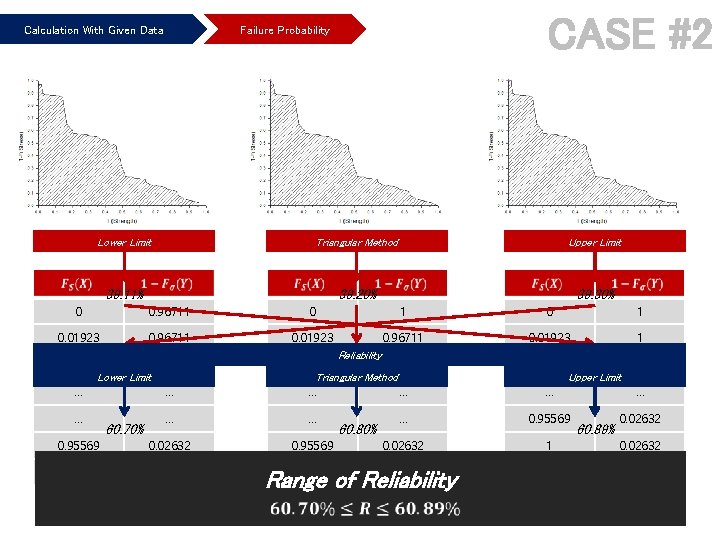
Calculation With Given Data CASE #2 Failure Probability Lower Limit Triangular Method Upper Limit 39. 11% 39. 20% 39. 30% 0 0. 96711 0. 01923 0. 96711 Lower Limit … … … 0 0. 01923 0. 96711 Triangular Method Reliability … … Triangular Method … … 0. 95569 0. 02632 0. 95569 0 60. 70% 1 60. 80% 0 1 0. 01923 1 Upper Limit 0. 01923 0. 96711 Upper Limit … … … 0. 95569 0. 02632 1 0 1 0 Range of Reliability 60. 89% 0. 02632

Conclusion Calculation Result Given Data Set Given Probability Density Function Integration From Minus Infinity Integration From Zero Lower Limit Triangular Method Upper Limit 60. 88% 60. 68% 60. 70% 60. 89% Reliability 60. 70% 60. 80% Integration From Zero 60. 90% Integration From Minus Infinite 60. 68% Lower Limit Triangular Method Upper Limit Q. What Might be Possible Cause of Error?

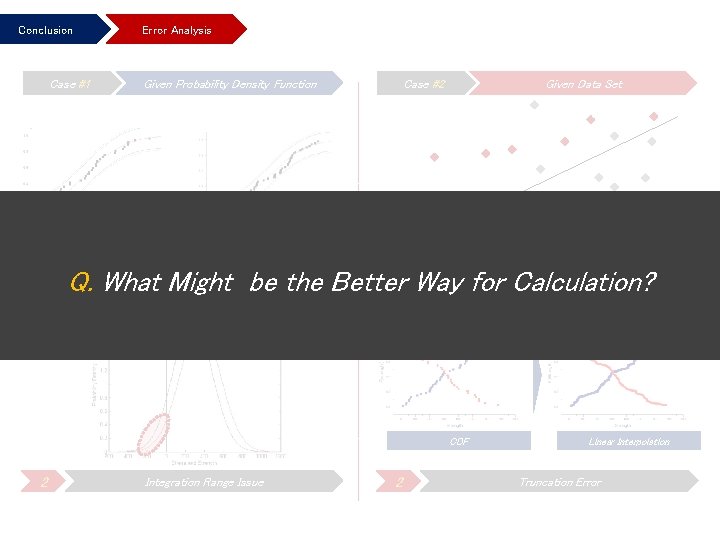
Conclusion Case #1 Error Analysis Given Probability Density Function Case #2 Given Data Set Actual Data Set#1 : : Stress 1 Data Set#2 : : Strength Picked Data Set Q. What. Significant Might be the Better 1 Way for Random Calculation? Level : 5% Disturbance CDF 2 Integration Range Issue 2 Linear Interpolation Truncation Error

Sepâs! Dhon-No-Baad! Merci! Thank You! 감사합니다 !

Qn. A