MAE 1202 AEROSPACE PRACTICUM Lecture 5 Compressible and

MAE 1202: AEROSPACE PRACTICUM Lecture 5: Compressible and Isentropic Flow 1 February 11, 2013 Mechanical and Aerospace Engineering Department Florida Institute of Technology D. R. Kirk

READING AND HOMEWORK ASSIGNMENTS • Reading: Introduction to Flight, by John D. Anderson, Jr. – For this week’s lecture: Chapter 4, Sections 4. 10 - 4. 21, 4. 27 – For next week’s lecture: Chapter 5, Sections 5. 1 - 5. 13 • Lecture-Based Homework Assignment: – Problems: 4. 7, 4. 11, 4. 18, 4. 19, 4. 20, 4. 23, 4. 27 • DUE: Friday, February 22, 2013 by 5 PM – Problems: 5. 2, 5. 3, 5. 4, 5. 6 • DUE: Friday, March 1, 2013 by 5 PM • Turn in hard copy of homework – Also be sure to review and be familiar with textbook examples in Chapter 5

ANSWERS TO LECTURE HOMEWORK • 5. 2: L = 23. 9 lb, D = 0. 25 lb, Mc/4 = -2. 68 lb ft – Note 1: Two sets of lift and moment coefficient data are given for the NACA 1412 airfoil, with and without flap deflection. Make sure to read axis and legend properly, and use only flap retracted data. – Note 2: The scale for cm, c/4 is different than that for cl, so be careful when reading the data • 5. 3: L = 308 N, D = 2. 77 N, Mc/4 = - 0. 925 N m • 5. 4: a = 2° • 5. 6: (L/D)max ~ 112

CREO DESIGN CONTEST • Create most elaborate, complex, stunning Aerospace Related project in Creo • Criteria: Assembly and/or exploded view • First place – Either increase your grade by an entire letter (C → B), or – Buy your most expensive textbook next semester • Second place: +10 points on final exam • Third place: +10 points on final exam

CAD DESIGN CONTEST

CAD DESIGN CONTEST

If you do the PRO|E challenge… Do not let it consume you!

BERNOULLI’S EQUATION Constant along a streamline • One of most fundamental and useful equations in aerospace engineering! • Remember: – Bernoulli’s equation holds only for inviscid (frictionless) and incompressible (r = constant) flows – Bernoulli’s equation relates properties between different points along a streamline – For a compressible flow Euler’s equation must be used (r is variable) – Both Euler’s and Bernoulli’s equations are expressions of F = ma expressed in a useful form for fluid flows and aerodynamics

EXAMPLE: MEASUREMENT OF AIRSPEED (4. 11) • How do we measure an airplanes speed in flight? • Pitot tubes are used on aircraft as speedometers (point measurement) 13

STATIC VS. TOTAL PRESSURE • In aerodynamics, 2 types of pressure: Static and Total (Stagnation) • Static Pressure, p – Due to random motion of gas molecules – Pressure we would feel if moving along with flow – Strong function of altitude • Total (or Stagnation) Pressure, p 0 or pt – Property associated with flow motion – Total pressure at a given point in flow is the pressure that would exist if flow were slowed down isentropically to zero velocity • p 0 ≥ p 14

MEASUREMENT OF AIRSPEED: INCOMPRESSIBLE FLOW Static pressure Dynamic pressure Total pressure Incompressible Flow

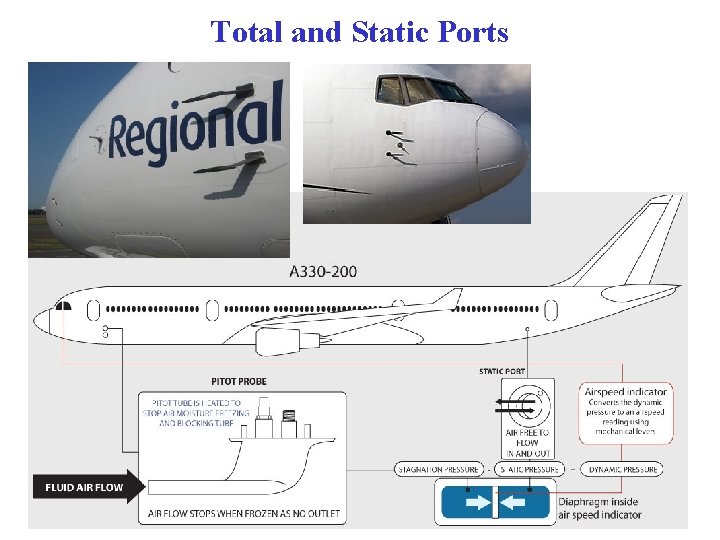
Total and Static Ports 16

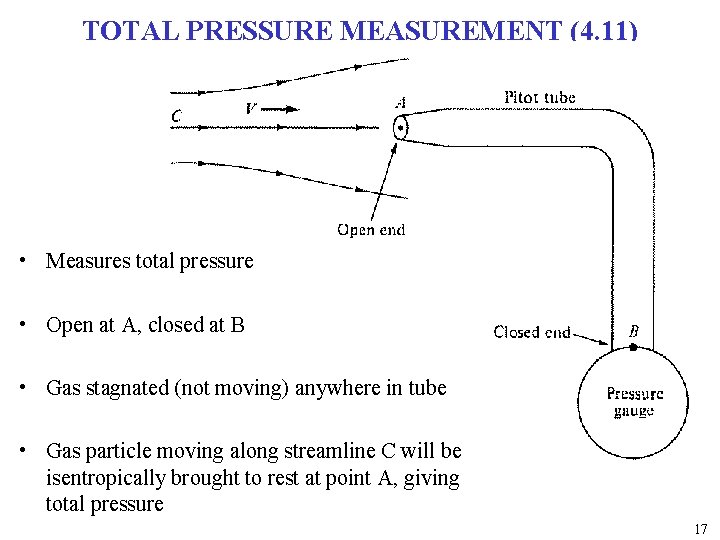
TOTAL PRESSURE MEASUREMENT (4. 11) • Measures total pressure • Open at A, closed at B • Gas stagnated (not moving) anywhere in tube • Gas particle moving along streamline C will be isentropically brought to rest at point A, giving total pressure 17

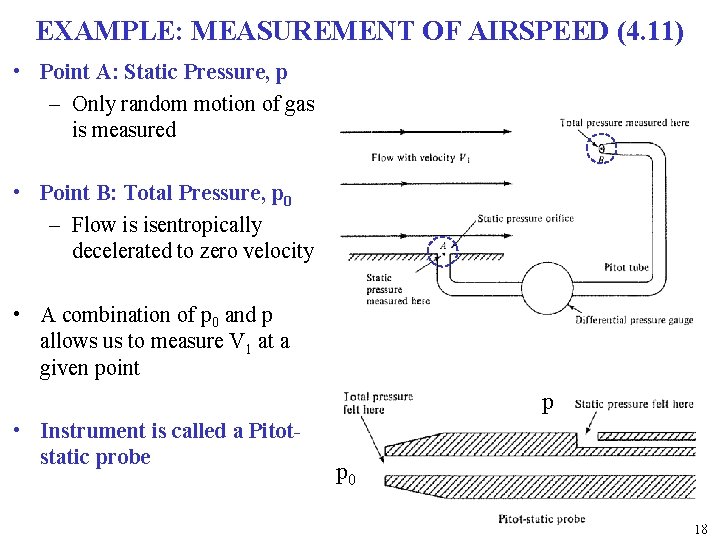
EXAMPLE: MEASUREMENT OF AIRSPEED (4. 11) • Point A: Static Pressure, p – Only random motion of gas is measured • Point B: Total Pressure, p 0 – Flow is isentropically decelerated to zero velocity • A combination of p 0 and p allows us to measure V 1 at a given point p • Instrument is called a Pitotstatic probe p 0 18

MEASUREMENT OF AIRSPEED: INCOMPRESSIBLE FLOW Static pressure Dynamic pressure Total pressure Incompressible Flow 19

TRUE VS. EQUIVALENT AIRSPEED • What is value of r? • If r is measured in actual air around the airplane • Measurement is difficult to do • Practically easier to use value at standard seal-level conditions, rs • This gives an expression called equivalent airspeed 20

TRAGIC EXAMPLE: Air France Crash • Aircraft crashed following an aerodynamic stall caused by inconsistent airspeed sensor readings, disengagement of autopilot, and pilot making nose-up inputs despite stall warnings • Reason for faulty readings is unknown, but it is assumed by accident investigators to have been caused by formation of ice inside pitot tubes, depriving airspeed sensors of forward-facing air pressure. • Pitot tube blockage has contributed to airliner crashes in the past 21

HOW DOES AN AIRFOIL GENERATE LIFT? • Lift due to imbalance of pressure distribution over top and bottom surfaces of airfoil (or wing) – If pressure on top is lower than pressure on bottom surface, lift is generated – Why is pressure lower on top surface? • We can understand answer from basic physics: – Continuity (Mass Conservation) – Newton’s 2 nd law (Euler or Bernoulli Equation) Lift Force = SPA

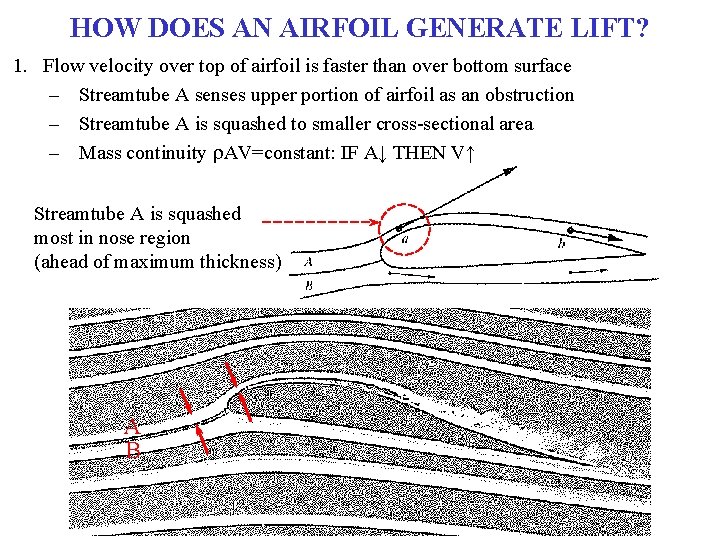
HOW DOES AN AIRFOIL GENERATE LIFT? 1. Flow velocity over top of airfoil is faster than over bottom surface – Streamtube A senses upper portion of airfoil as an obstruction – Streamtube A is squashed to smaller cross-sectional area – Mass continuity r. AV=constant: IF A↓ THEN V↑ Streamtube A is squashed most in nose region (ahead of maximum thickness) A B

HOW DOES AN AIRFOIL GENERATE LIFT? 2. As V ↑ p↓ – Incompressible: Bernoulli’s Equation – Compressible: Euler’s Equation – Called Bernoulli Effect 3. With lower pressure over upper surface and higher pressure over bottom surface, airfoil feels a net force in upward direction → Lift Most of lift is produced in first 20 -30% of wing (just downstream of leading edge) Can you express these ideas in your own words?

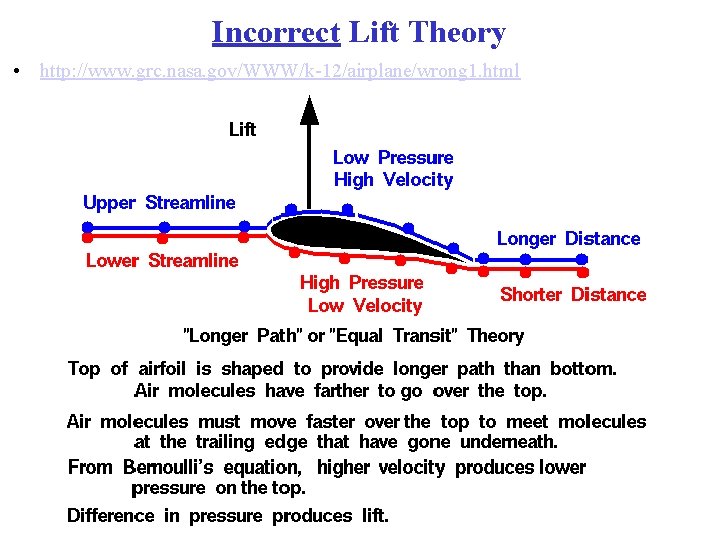
Incorrect Lift Theory • http: //www. grc. nasa. gov/WWW/k-12/airplane/wrong 1. html

SUMMARY OF GOVERNING EQUATIONS (4. 8) • Steady, incompressible flow of an inviscid (frictionless) fluid along a streamline or in a stream tube of varying area • Most important variables: p and V • T and r are constants throughout flow What if flow is high speed, M > 0. 3? What if there are temperature effects? How does density change? continuity Bernoulli

1 st LAW OF THERMODYNAMICS (4. 5) Boundary System Surroundings e (J/kg) • System (gas) composed of molecules moving in random motion • Energy of molecular motion is internal energy per unit mass, e, of system • Only two ways e can be increased (or decreased): 1. Heat, dq, added to (or removed from) system 2. Work, dw, is done on (or by) system

THOUGHT EXPERIMENT #1 • Do not allow size of balloon to change (hold volume constant) • Turn on a heat lamp • Heat (or q) is added to the system • How does e (internal energy per unit mass) inside the balloon change?

THOUGHT EXPERIMENT #2 • *You* take balloon and squeeze it down to a small size • When volume varies work is done • Who did the work on the balloon? • How does e (internal energy per unit mass) inside the balloon change? • Where did this increased energy come from?

1 st LAW OF THERMODYNAMICS (4. 5) Boundary e (J/kg) SYSTEM (unit mass of gas) SURROUNDINGS dq • System (gas) composed of molecules moving in random motion • Energy of all molecular motion is called internal energy per unit mass, e, of system • Only two ways e can be increased (or decreased): 1. Heat, dq, added to (or removed from) system 2. Work, dw, is done on (or by) system

1 st LAW IN MORE USEFUL FORM (4. 5) • 1 st Law: de = dq + dw – Find more useful expression for dw, in terms of p and r (or v = 1/r) Change in Volume (-) • When volume varies → work is done • Work done on balloon, volume ↓ • Work done by balloon, volume ↑

ENTHALPY: A USEFUL QUANTITY (4. 5) Define a new quantity called enthalpy, h: (recall ideal gas law: pv = RT) Differentiate Substitute into 1 st law (from previous slide) Another version of 1 st law that uses enthalpy, h:

HEAT ADDITION AND SPECIFIC HEAT (4. 5) • Addition of dq will cause a small change in temperature d. T of system dq d. T • Specific heat is heat added per unit change in temperature of system • Different materials have different specific heats – Balloon filled with He, N 2, Ar, water, lead, uranium, etc… • ALSO, for a fixed dq, resulting d. T depends on type of process…

SPECIFIC HEAT: CONSTANT PRESSURE • Addition of dq will cause a small change in temperature d. T of system • System pressure remains constant dq d. T Extra Credit #1: Show this step

SPECIFIC HEAT: CONSTANT VOLUME • Addition of dq will cause a small change in temperature d. T of system • System volume remains constant dq d. T Extra Credit #2: Show this step

HEAT ADDITION AND SPECIFIC HEAT (4. 5) • Addition of dq will cause a small change in temperature d. T of system • Specific heat is heat added per unit change in temperature of system • However, for a fixed dq, resulting d. T depends on type of process: Constant Pressure Constant Volume Specific heat ratio For air, g = 1. 4

ISENTROPIC FLOW (4. 6) • Goal: Relate Thermodynamics to Compressible Flow • Adiabatic Process: No heat is added or removed from system – dq = 0 – Note: Temperature can still change because of changing density • Reversible Process: No friction (or other dissipative effects) • Isentropic Process: (1) Adiabatic + (2) Reversible – (1) No heat exchange + (2) no frictional losses – Relevant for compressible flows only – Provides important relationships among thermodynamic variables at two different points along a streamline g = ratio of specific heats g = cp/cv gair=1. 4

DERIVATION: ENERGY EQUATION (4. 7) Energy can neither be created nor destroyed Start with 1 st law Adiabatic, dq=0 1 st law in terms of enthalpy Recall Euler’s equation Combine Integrate Result: frictionless + adiabatic flow

ENERGY EQUATION SUMMARY (4. 7) • Energy can neither be created nor destroyed; can only change physical form – Same idea as 1 st law of thermodynamics Energy equation for frictionless, adiabatic flow (isentropic) h = enthalpy = e+p/r = e+RT h = cp. T for an ideal gas Also energy equation for frictionless, adiabatic flow Relates T and V at two different points along a streamline

SUMMARY OF GOVERNING EQUATIONS (4. 8) STEADY AND INVISCID FLOW • Incompressible flow of fluid along a streamline or in a stream tube of varying area • Most important variables: p and V • T and r are constants throughout flow • Compressible, isentropic (adiabatic and frictionless) flow along a streamline or in a stream tube of varying area • T, p, r, and V are all variables continuity isentropic energy equation of state at any point continuity Bernoulli

EXAMPLE: SPEED OF SOUND (4. 9) • Sound waves travel through air at a finite speed • Sound speed (information speed) has an important role in aerodynamics • Combine conservation of mass, Euler’s equation and isentropic relations: • Speed of sound, a, in a perfect gas depends only on temperature of gas • Mach number = flow velocity normalizes by speed of sound – If M < 1 flow is subsonic – If M = 1 flow is sonic – If M > flow is supersonic • If M < 0. 3 flow may be considered incompressible

KEY TERMS: CAN YOU DEFINE THEM? • Streamline • Stream tube • Constant pressure process • Constant volume process • Steady flow • Unsteady flow • Adiabatic • Reversible • Viscid flow • Inviscid flow • Compressible flow • Incompressible flow • Laminar flow • Turbulent flow • Isentropic • Enthalpy

MEASUREMENT OF AIRSPEED: SUBSONIC COMRESSIBLE FLOW • If M > 0. 3, flow is compressible (density changes are important) • Need to introduce energy equation and isentropic relations cp: specific heat at constant pressure M 1=V 1/a 1 gair=1. 4

MEASUREMENT OF AIRSPEED: SUBSONIC COMRESSIBLE FLOW • So, how do we use these results to measure airspeed p 0 and p 1 give Flight Mach number Mach meter M 1=V 1/a 1 Actual Flight Speed using pressure difference What is T 1 and a 1? Again use sea-level conditions Ts, as, ps (a 1=340. 3 m/s)

EXAMPLE: TOTAL TEMPERATURE Total temperature Static temperature Vehicle flight Mach number • A rocket is flying at Mach 6 through a portion of the atmosphere where the static temperature is 200 K • What temperature does the nose of the rocket ‘feel’? • T 0 = 200(1+ 0. 2(36)) = 1, 640 K!

MEASUREMENT OF AIRSPEED: SUPERSONIC FLOW • What can happen in supersonic flows? • Supersonic flows (M > 1) are qualitatively and quantitatively different from subsonic flows (M < 1)

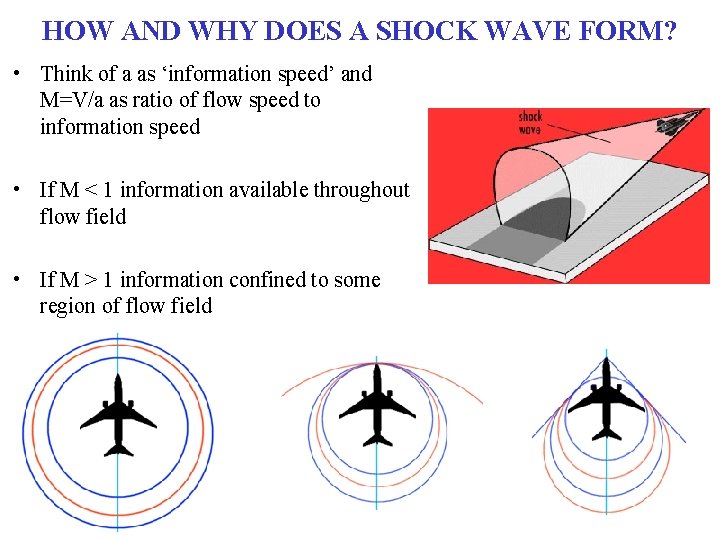
HOW AND WHY DOES A SHOCK WAVE FORM? • Think of a as ‘information speed’ and M=V/a as ratio of flow speed to information speed • If M < 1 information available throughout flow field • If M > 1 information confined to some region of flow field

MEASUREMENT OF AIRSPEED: SUPERSONIC FLOW Notice how different this expression is from previous expressions You will learn a lot more about shock wave in compressible flow course

SUMMARY OF AIR SPEED MEASUREMENT • Subsonic, incompressible • Subsonic, compressible • Supersonic

HOW ARE ROCKET NOZZLES SHAPPED?

MORE ON SUPERSONIC FLOWS (4. 13) Isentropic flow in a streamtube Differentiate Euler’s Equation Since flow is isentropic a 2=dp/dr Area-Velocity Relation

CONSEQUENCES OF AREA-VELOCITY RELATION • IF Flow is Subsonic (M < 1) – For V to increase (d. V positive) area must decrease (d. A negative) – Note that this is consistent with Euler’s equation for d. V and dp • IF Flow is Supersonic (M > 1) – For V to increase (d. V positive) area must increase (d. A positive) • IF Flow is Sonic (M = 1) – M = 1 occurs at a minimum area of cross-section – Minimum area is called a throat (d. A/A = 0)

TRENDS: CONTRACTION 1: INLET 2: OUTLET M 1 < 1 V 2 > V 1 M 1 > 1 V 2 < V 1

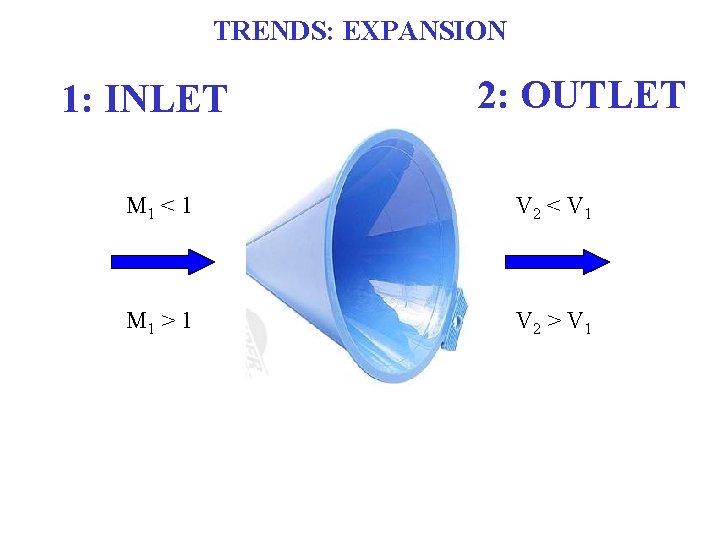
TRENDS: EXPANSION 1: INLET 2: OUTLET M 1 < 1 V 2 < V 1 M 1 > 1 V 2 > V 1

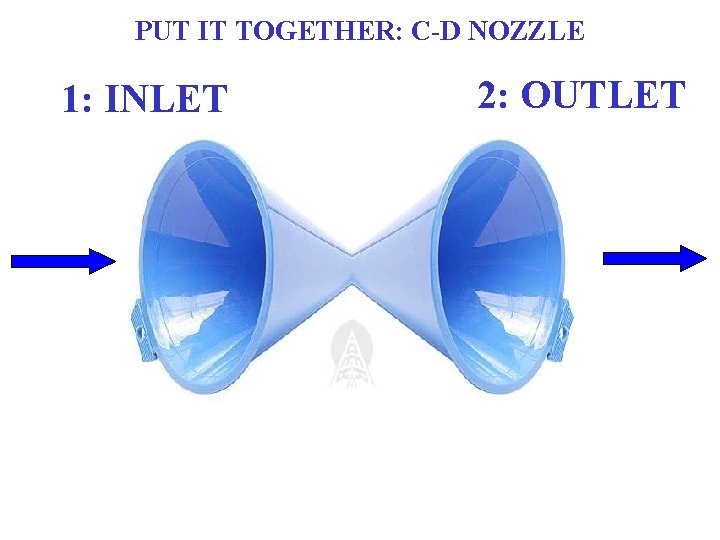
PUT IT TOGETHER: C-D NOZZLE 1: INLET 2: OUTLET

MORE ON SUPERSONIC FLOWS (4. 13) • A converging-diverging, with a minimum area throat, is necessary to produce a supersonic flow from rest Supersonic wind tunnel section Rocket nozzle

SUMMARY OF GOVERNING EQUATIONS (4. 8) STEADY AND INVISCID FLOW • Incompressible flow of fluid along a streamline or in a stream tube of varying area • Most important variables: p and V • T and r are constants throughout flow • Compressible, isentropic (adiabatic and frictionless) flow along a streamline or in a stream tube of varying area • T, p, r, and V are all variables continuity isentropic energy equation of state at any point continuity Bernoulli