MACSSE 474 Theory of Computation More on showing







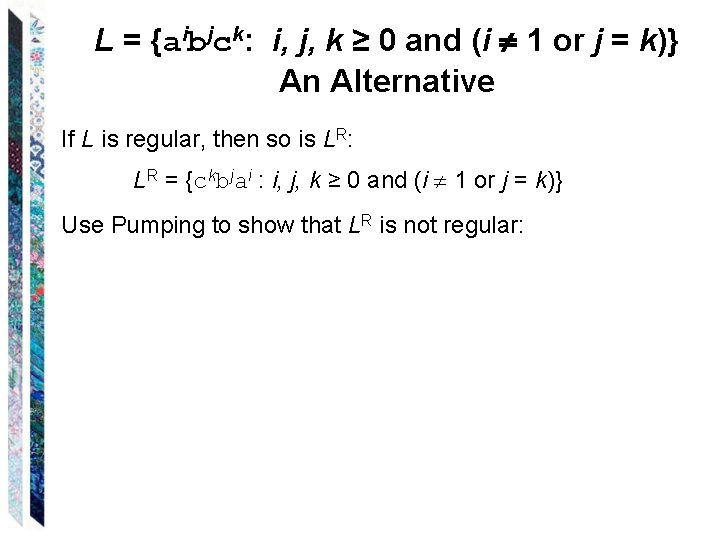









- Slides: 19

MA/CSSE 474 Theory of Computation More on showing L non-regular (Using Closure) Decision Problems

Your Questions? • Previous class days' material • Reading Assignments • 8 problems • Anything else This one has so many levels …

L = {aibj: i, j 0 and i j} Try to use the Pumping Theorem by letting w = akbk+k!. Then y = ap for some nonzero p. Let q = (k!/p) + 1 (i. e. , pump in (k!/p) times). Note that (k!/p) must be an integer because p <= k. The number of a’s in the new string is k + (k!/p)p = k + k!. So the new string is ak+k!bk+k!, which has equal numbers of a’s and b’s and so is not in L.

L = {aibj: i, j 0 and i j} An easier way: If L is regular then so is L. Is L regular? L = An. Bn {strings with a and b out of order} If L is regular, then so is L = L a*b* = ______
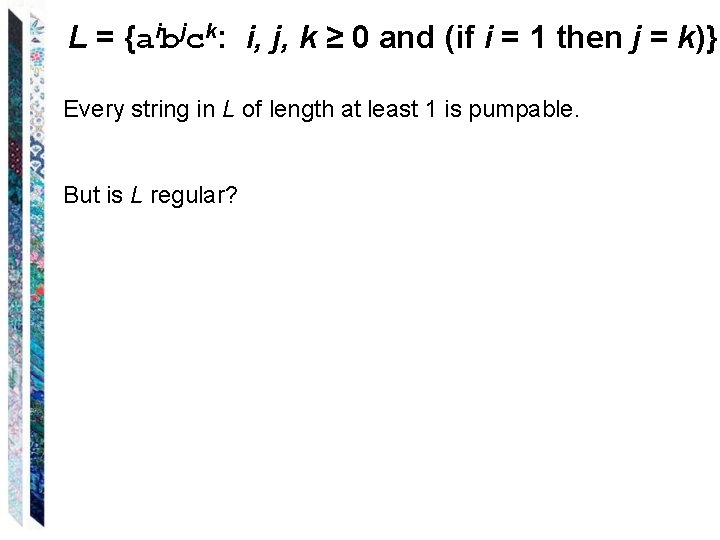
L = {aibjck: i, j, k ≥ 0 and (if i = 1 then j = k)} Every string in L of length at least 1 is pumpable. But is L regular?

L = {aibjck: i, j, k ≥ 0 and (if i = 1 then j = k)} Every string in L of length at least 1 is pumpable. Rewrite the final condition as: (i 1) or (j = k)

L = {aibjck: i, j, k ≥ 0 and (i 1 or j = k)} Every string in L of length at least 1 is pumpable: • If w has i = 0: if j 0, let y be b; otherwise, let y be c. Let q=0 or q>1. In each case i will still be 0 and thus not equal to 1, so the resulting string is in L. • If i = 1: let y be a. Let q=0 or q>1. Then i will no longer equal 1, so the resulting string is in L. • If i = 2: let y be aa. Let q=0 or q>1. Then i cannot equal 1, so the resulting string is in L. • If i > 2: let y = a. Let q=0 or q>1. Then i cannot equal 1, so the resulting string is in L.

L = {aibjck: i, j, k ≥ 0 and (i 1 or j = k)} But the closure theorems help. Suppose we guarantee that i = 1. If L is regular, then so is: L = L ab*c*. L = {abjck : j, k ≥ 0 and j = k} We can easily use the Pumping Theorem to show that L is not regular:
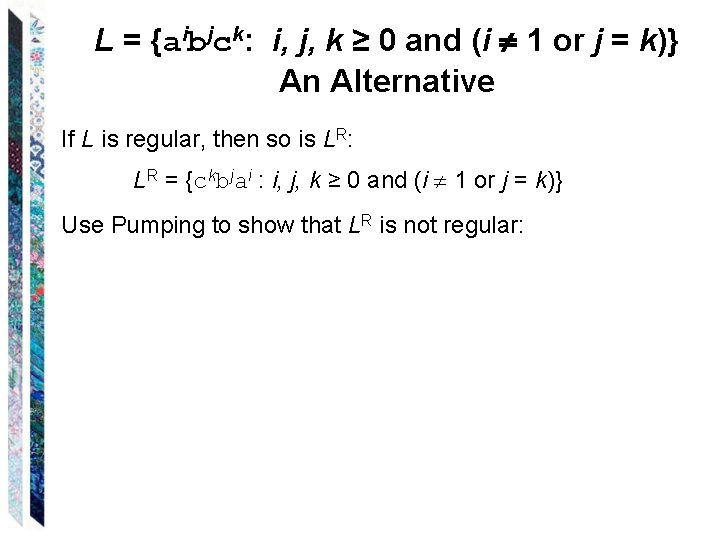
L = {aibjck: i, j, k ≥ 0 and (i 1 or j = k)} An Alternative If L is regular, then so is LR: LR = {ckbjai : i, j, k ≥ 0 and (i 1 or j = k)} Use Pumping to show that LR is not regular:

Functions from one Language to Another Let firstchars(L) = {w : y L ( y = cx, c L , x L*, and w c*)} Is the set of regular languages closed under firstchars? L a*b* ca*cb* firstchars(L)

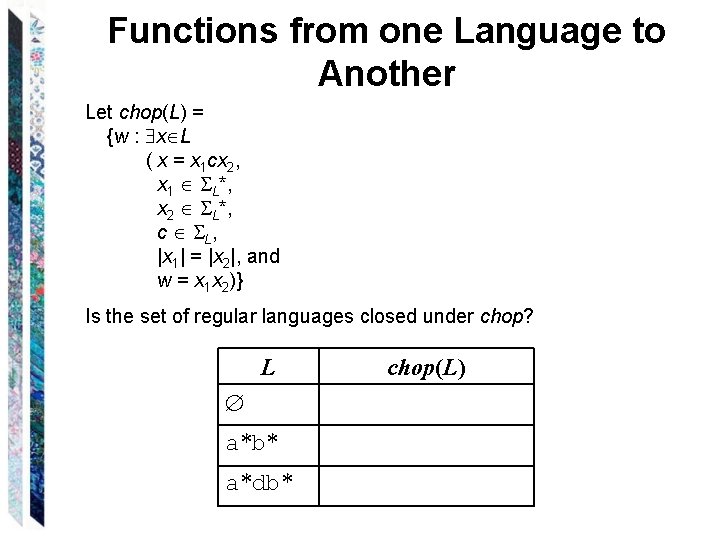
Functions from one Language to Another Let chop(L) = {w : x L ( x = x 1 cx 2, x 1 L*, x 2 L*, c L , |x 1| = |x 2|, and w = x 1 x 2)} Is the set of regular languages closed under chop? L a*b* a*db* chop(L)

Functions from One Language to Another Let maxstring(L) = {w: w L, z * (z wz L)} Is the set of regular languages closed under maxstring? L a*b* ab*a a*b*a maxstring(L)

The rest of Session 16's slides • (previous session) • They are there as examples in case they are helpful for you as you do HW 8 • Next session we may or may not do some of these examples in class. • Most of them are discussed in detail in the textbook.

Summary of algorithms we have so far The next few slides are here for reference. I do not expect to spend class time on them. You should know how to do all of them, but during class exercises and homework you may simply "call" any of them as part of your decision procedures. ● Operate on FSMs without altering the language that is accepted: ● ndfsmtodfsm(M: NDFSM) ● min. DFSM (M: DFSM) ● build. FSMcanonicalform(M: FSM)

Summary of Algorithms ● Compute functions of languages defined as FSMs: ● Given FSMs M 1 and M 2, construct a FSM M 3 such that L(M 3) = L(M 2) L(M 1). ● Given FSMs M 1 and M 2, construct a new FSM M 3 such that L(M 3) = L(M 2) L(M 1). ● Given FSM M, construct an FSM M* such that L(M*) = (L(M))*. ● Given a DFSM M, construct an FSM M* such that L(M*) = L(M). ● Given two FSMs M 1 and M 2, construct an FSM M 3 such that L(M 3) = L(M 2) L(M 1). ● Given two FSMs M 1 and M 2, construct an FSM M 3 such that L(M 3) = L(M 2) - L(M 1). ● Given an FSM M, construct an FSM M* such that L(M*) = (L(M))R. ● Given an FSM M, construct an FSM M* that accepts letsub(L(M)).

Algorithms, Continued ● Converting between FSMs and regular expressions: ● Given a regular expression , construct an FSM M such that: L( ) = L(M) ● Given an FSM M, construct a regular expression such that: L( ) = L(M) ● Algorithms that implement operations on languages defined by regular expressions: any operation that can be performed on languages defined by FSMs can be implemented by converting all regular expressions to equivalent FSMs and then executing the appropriate FSM algorithm.

Algorithms, Continued ● Converting between FSMs and regular grammars: ● Given a regular grammar G, construct an FSM M such that: L(G) = L(M) ● Given an FSM M, construct a regular grammar G such that: L(G) = L(M). We have not yet discussed regular grammars. They are in the reading assignment for tomorrow. This is here for completeness.

Decision Procedures A decision procedure is an algorithm whose result is a Boolean value (in this course's context, sometimes we will write "yes" or "no" instead of "true" or "false"). It must: ● Halt, no matter what (correctly typed) input it is given. ● Always give the correct answer Usually a decision procedure has one or more parameters Zero-parameter decision procedures are not very interesting!

Answering Specific Questions Given two regular expressions 1 and 2, is: (L( 1) L( 2)) – { } ? 1. From 1, construct an FSM M 1 such that L( 1) = L(M 1). 2. From 2, construct an FSM M 2 such that L( 2) = L(M 2). 3. Construct M such that L(M ) = L(M 1) L(M 2). 4. Construct M such that L(M ) = { }. 5. Construct M such that L(M ) = L(M ) - L(M ). 6. If L(M ) is empty return False; else return True. (in tomorrow's exercises, you'll write an algorithm for step 6) For practice later: Given two regular expressions 1 and 2, are there at least 3 strings that are generated by both of them?