Macroscopic Mechanical Energy Balance CBE 150 A Transport

Macroscopic Mechanical Energy Balance CBE 150 A – Transport Spring Semester 2014

Macroscopic Energy Balance Accumulation = In – Out + {Generation – Consumption} Assume: • Energy is conserved • Steady State CBE 150 A – Transport Spring Semester 2014

Macroscopic Energy Balance How may Energy enter System? Note: Q and W positive for energy into system 1. Via Mass Flow • KE • PE • Int. Energy 2. Heat Transfer (Q) • Conduction • Radiation 3. Work on or by System (W) • Pumps • Compressors • CBE 150 A – Transport Spring Semester 2014

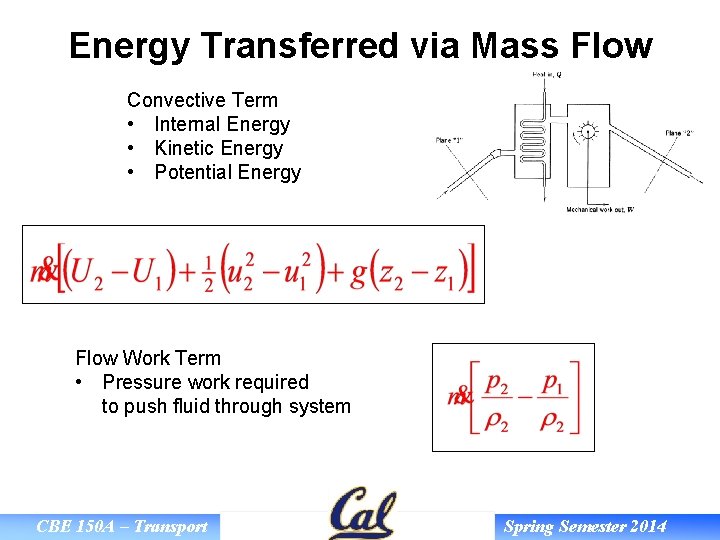
Energy Transferred via Mass Flow Convective Term • Internal Energy • Kinetic Energy • Potential Energy Flow Work Term • Pressure work required to push fluid through system CBE 150 A – Transport Spring Semester 2014

Overall Mechanical Energy Balance CBE 150 A – Transport Spring Semester 2014

Mechanical Energy Balance CBE 150 A – Transport Spring Semester 2014

Variable Velocity at Cross Section Again integrate across section and introduce correction factor, a, to allow use of average velocity. CBE 150 A – Transport Spring Semester 2014

Variable Velocity at Cross Section Laminar Flow Parabolic Flow Turbulent Flow Plug Flow CBE 150 A – Transport α= 2 α≈ Spring Semester 2014

MEB with Correction for Variable Velocity Historical Note: Though this result is often called the Bernoulli equation, Bernoulli actually only ˆ considered W = hf = 0. Daniel Bernoulli (1700 - 1782) CBE 150 A – Transport Spring Semester 2014

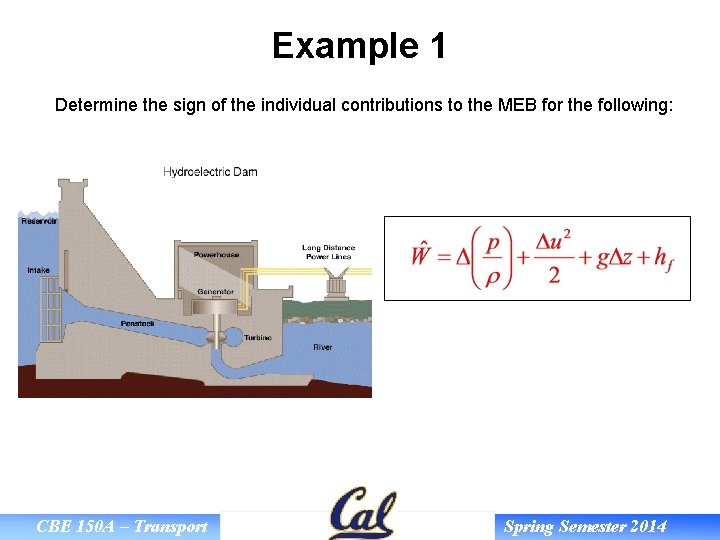
Example 1 Determine the sign of the individual contributions to the MEB for the following: CBE 150 A – Transport Spring Semester 2014

Example 2 - Bernoulli and the airplane Cessna 172 CBE 150 A – Transport Spring Semester 2014

Cessna 172 Data • Gross weight = 2300 lbs • Normal cruising speed = 65 mph • Wing surface area = 160 ft 2 • Upper wing path length = 1. 016 X lower wing path length CBE 150 A – Transport Spring Semester 2014

CBE 150 A – Transport Spring Semester 2014

Mechanical Energy Balance 10 minute problem Water with a density of 998 kg/m 3 is flowing at a steady mass rate through a uniform diameter pipe. The Reynolds number in the pipe is approximately 4000. The pump supplies 155. 4 J/kg of fluid flowing through the pipe. Given the other conditions shown on the diagram, calculate the viscous dissipation, hf, in the pipe system. CBE 150 A – Transport Spring Semester 2014