Macroscopic Maxwells equations The concept of fields was

Macroscopic Maxwell’s equations • The concept of fields was introduced to explain “action at distance. ” The physical observables are forces. • Macroscopic Maxwell’s equations deal with fields that are local spatial averages over microscopic fields associated with discrete charges. Charge and current densities are considered as continuous functions of space.

Continuity equation Take divergence zero for any vector field (continuity equation) The conservation of charge is implicitly contained in Maxwell’s equations.

Constitutive relations Maxwell’s equations are incomplete. The fields are connected to one another by constitutive relations (material equations) describing the electromagnetic response of media. Polarization – material dependent! −− −− ++ ++ Magnetization

Relation between D and E Response function (tensor) −− −− ++ ++ Assumptions: • a linear medium (P is proportional to E) • an isotropic medium • an instantaneous response (no temporal dispersion) • a local response (no spatial dispersion)

Response Temporal dispersion: P (or D) at time t depends on E at all times t′ previous to t (non-instantaneous response). Temporal dispersion is widely encountered phenomenon and it is important to accurately take it into account. −− −− ++ ++ Spatial dispersion: P (or D) at a point [x, y, z] also depends on the values of the electric field at neighboring points [x′, y′, z′]. A spatially dispersive medium is therefore also called a nonlocal medium. Nonlocal effects can be observed at interfaces between different media or in metallic objects with sizes comparable with the mean-free path of electrons. In most cases of interest the effect is very week and we can safely ignore it.

(a bit of math) use the four-dimensional Fourier transform the spatial frequency of the field the angular frequency of the field (the inverse Fourier transform ≡ IFT) (the Fourier transform ≡ FT)

Constitutive relations use the four-dimensional Fourier transform the spatial frequency of the field −− −− ++ ++ the angular frequency of the field

Constitutive relations use the four-dimensional Fourier transform −− −− ++ ++ (dielectric constant) obtained in a similar fashion

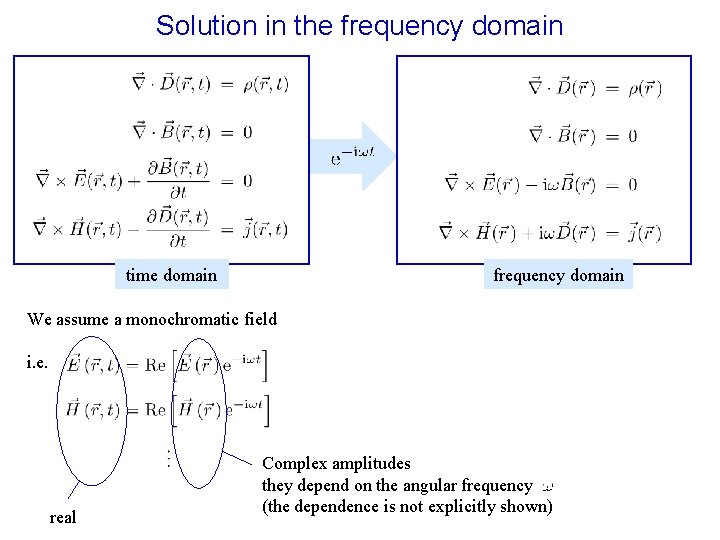
Solution in the frequency domain time domain frequency domain We assume a monochromatic field i. e. real Complex amplitudes they depend on the angular frequency (the dependence is not explicitly shown)

Solution in the frequency domain time domain frequency domain The same Eqs. are obtained for the spectral components not shown time dependent field (real) (IFT) its spectrum (complex) (FT) (a consequence for the spectral components)

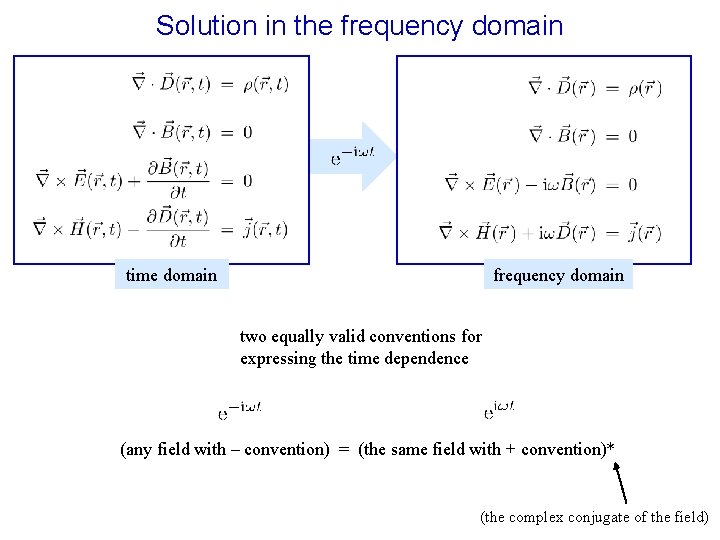
Solution in the frequency domain time domain frequency domain two equally valid conventions for expressing the time dependence (any field with – convention) = (the same field with + convention)* (the complex conjugate of the field)

Solution in the frequency domain time domain frequency domain ? For simpler notation, textbook authors often drop the argument in the fields and material parameters. It is the context of the problem which determines which of the fields is used.

Complex dielectric constant check this! no source current! we will call it “complex” dielectric constant and denote again with

Complex dielectric constant no source current! • Just handy convention – it will be used here. • The formulation does not distinguish between conduction currents (free charges) and polarization currents (bound charges). • Energy dissipation is associated with the imaginary part of the dielectric constant.

The complex form of Maxwell’s equations check that they follow from. . . . independent Eqs. we will solve them