Macromechanical behavior of a laminate Classical lamination theory

Macromechanical behavior of a laminate Classical lamination theory - Hypothesis - Variations of stress and deformation in the laminate - Force and moment resultant Special cases of laminate stiffness - Single-ply laminates - Symmetric laminates - Antisymmetric laminates - Nonsymmetric laminates

Definition of laminate • Laminate: Two or more laminae stacked together (in the thickness z direction) at various orientations thus acting as a single structural element

Classical lamination theory • The classical lamination theory allows, starting from the elastic constants of each lamina, to calculate the mechanical properties of the whole laminate. • The fiber direction of each lamina is oriented in order to obtain a laminate able to withstand loads in various directions depending on the applied stresses • Hypothesis: • The laminate is made with laminae perfectly bonded to each other. • The bonding surfaces are infinitely thin and not deformable in shear, i. e. , the strains are continuous between a lamina and the other and there is no relative slippage of a lamina relative to each other • Plane stress state • Thin plates with small deflections (the laminate is thin with two dimensions >> of the others) • z= xz= yz=0 Kirchoff’s hypothesis: a line normal to the median plane (ABCD) remains perpendicular to it ( xz= yz=0) and with the same length ( z=0) due to extensions and bending of the laminate • The laminate acts as a flat plate whose special mechanical properties are defined by the properties of the constituent laminae. (It behaves like a single layer consisting of a material characterized by “special” properties).

Kirchoff’s hypothesis • If the laminate is thin, a line AD originally straight and perpendicular to the middle surface of the laminate, is assumed to remain straight and perpendicular to the middle surface when the laminate is extended and bent. x y, v u 0 z A /2 A B D D z, w x, u Undeformed cross section Geometry of deformation in the x-z plane A /2 B D Deformed cross section

Kirchoff’s hypothesis • dx B z. C C D A dw 0

Kirchoff’s hypothesis •

Laminae stresses •

Effect of loading conditions- pure tension • Pure tension • Isotropic z z 0 0 • Laminate 0/90/90/0 z 0 90 90 0 E 1 0 E 2 0 E 1 E 2 E 1 0 0 E 0

Effect of loading conditions: pure bending • Pure bending • Isotropic z z Neutral axis 0 0 z 90 0 0 90 • Laminate 90/0/0/90 • Laminate 0/90/90/0 0 z 0 90 90 0 0 E 2 E 1 E 2 Neutral axis E E 1 E 2 E 1 0 Neutral axis E 0

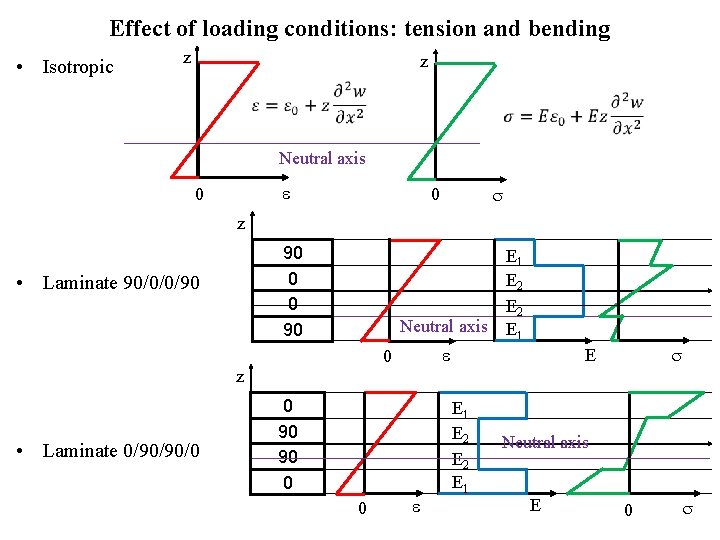
Effect of loading conditions: tension and bending • Isotropic z z Neutral axis 0 0 z 90 0 0 90 • Laminate 90/0/0/90 Neutral axis • Laminate 0/90/90/0 0 z 0 90 90 0 0 E 1 E 2 E 1 E E 1 E 2 E 1 Neutral axis E 0

Effect of loading conditions: tension and bending z • Isotropic z Neutral axis 0 0 z • Arbitrary laminate 1 2 3 Neutral axis 4 0 laminate E 0

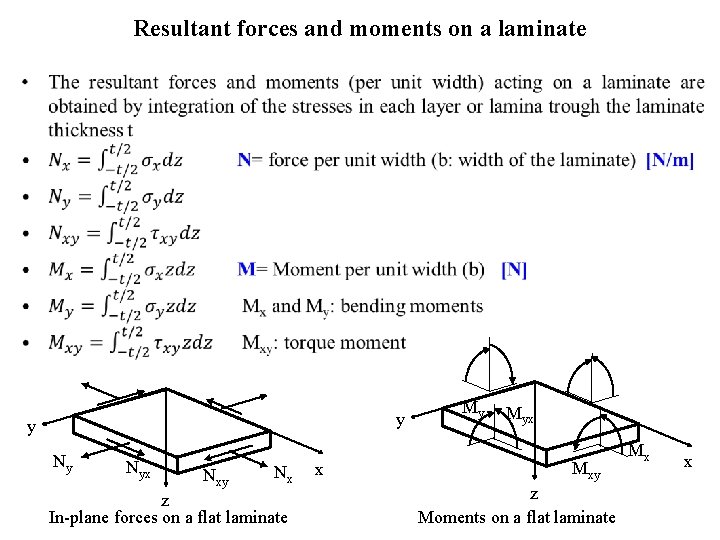
Resultant forces and moments on a laminate • y y Ny Nyx Nxy Nx z In-plane forces on a flat laminate x My Myx Mxy z Moments on a flat laminate Mx x

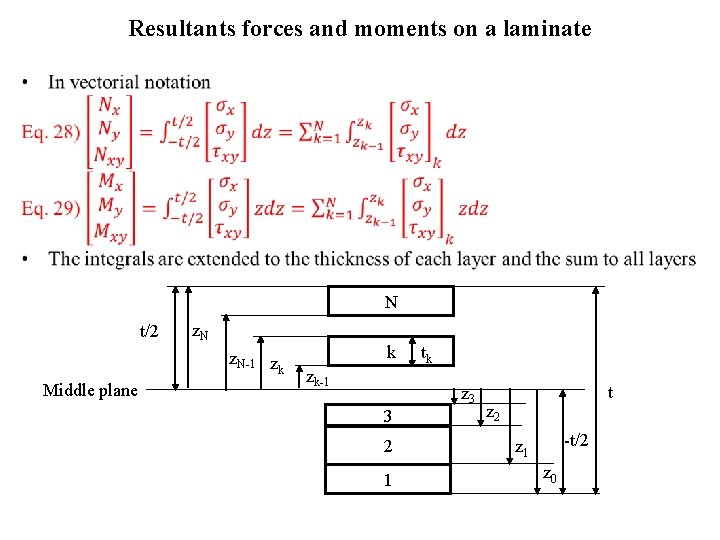
Resultants forces and moments on a laminate • N t/2 z. N-1 z k Middle plane k zk-1 3 2 1 tk z 3 t z 2 -t/2 z 1 z 0

Resultants forces and moments on a laminate •

Laminate stiffnesses •

Laminate stiffness matrix •

Physical interpretation •

Physical interpretation xy • A 16 and A 26 involve in-plane deformations y x x z Nx • D 16 and D 26 involve torsion due to bending My kxy ky • B terms involve out of plane deformation (bending and torsion) due to in plane stress and viceversa x kxy Nx ky

Inverse relationships •

Constitutive equation of laminate and stiffness matrices •

Terms of the A matrix • h 0 zj zi-1 h 0 zi zj-1

Terms of the B matrix • h 0 zj zi-1 h 0 zi zj-1

Terms of the D matrix • h 0 zj zi-1 h 0 zi zj-1

Some simplifications of the laminate stiffness matrix •

Stiffness for a single isotropic ply •

Stiffness for a single specially orthotropic ply •

Stiffness of a single generally orthotropic ply •

stiffness of a single anisotropic ply •

Typical lamina and laminate • Single ply – – Isotropic Specially orthotropic Generally orthotropic Anisotropic • laminate – symmetric – antisymmetric – non symmetric S: symmetric; k=Kevlar; C=carbon; G=glass Type of laminate Stacking sequence unidirectional [0°/0°/0°/0°]=[0° 6] Cross-ply symmetric [0°/90°/0°]=[0°/90°]S Angle-ply symmetric [45°/-45°/45°]=[45°/-45°]S=[+45°]S Angle-ply antisymmetric [30°/-30°/+30°/-30°/30°/-30°]=[30°/-30°]4=[+30°]4 Quasi isotropic [0°/+45°/90°] Symmetric quasi isotropic [0°/+45°/-45°/90/90°/-45/45°/90°]=[0°/+45°/90]S Multidirectional [0°/45°/30°/-30°/45°] Hybrid [0 k/0 k/45 c/-45 c/90 g/-45 c/0 k/0 k]=[02 k/+45 c/90 g]S

Typical lamina and laminate • Unidirectional laminate: the fiber orientation angles are the same in all laminas. For example, in unidirectional 0°laminates, =0° in all laminas. • Cross-ply laminate: the fiber orientation angles in alternate plies are /0/90 • Angle-ply laminate: the fiber orientation angles in alternate plies are / /- / when 0° or 90° • Quasi-isotropic laminate: produced using at least three different ply orientations, all with equal angles between them. It exhibits quasi-isotropic extensional stiffness properties.

Typical lamina and laminate • 0 0 90 90 0

Typical lamina and laminate Angle ply laminates: They consist of orthotropic layers stuck on each other with principal material directions alternating at + °and - ° Nb: with an even number of plies they are antisymmetric Nb: with an odd number of plies they are symmetric + - + - + - +

Symmetric laminates • • • Symmetric laminate: the ply orientation is symmetrical about the center line of the laminate; that is, for each ply above the midplane, there is an identical ply (in material, thickness, and fiber orientation angle) at an equal distance below the midplane (z)= (-z) Symmetric laminates are preferred in order to limit the component distortion due both to thermal contractions caused by the curing or consolidation cycle and to the coupling of deformations as a consequence of external loads. Even number of plies Plane of symmetry x 90° • 0° 0° 30° 0° 0° 90° [90/02/30]S Odd number of plies: The bar over 0 indicates that the plane of symmetry passes midway through the thickness of the 0° ply Plane of symmetry x 90° 0° 0° 30° 0° 0° 90°

Laminate stacking sequence and notation +45 0 0 90 0 +45 -45 [+45/90/-45]S 0 [06]T -45 0 -45 90 0 +45 -45 90 0 0 0 90 +45 90 0 -45 0 90 0 +45 -45 90 -45 45 0 0 [0/+45]S "S" subscript is for symmetric "T" subscript is for total [(+45/0)3]T

Laminates Symmetric and balanced laminate: /- /- / [B]=0 The laminae must have the same thickness h 0 and same distance z from the midplane and must be of the same material and orientation Balanced antysimmetric laminate: A 16=A 26=0 Respect to the midplane, the laminae have the same thickness t 0 and orientation + , but can be at difference distance e. g. [0/+30/-30/0] Antisymmetric laminate /- / /- The laminae must have the same thickness h 0 and same distance z from the midplane, must be of the same material and have orientation - D 16=D 26=0 and A 16=A 26=0 B 11 e B 12 0 Non symmetric laminate: there is no symmetry or antisymmetry. Ex: 0/0/0/90/90/90 and 0/ / /90. h 0 + z 1 h 0 + + z 1 z 2 h 0 - h 0 + z 1 h 0 -

Symmetric laminates • • Material, angle and thickness of the layers are the same above and below the mid-plane For each ply above the midplane there is an identical ply (for material orientation, thickness and distance from the midplane) below the midplane. symmetric h 0 -30° h 3 60° h 2 45° h 1 60° h 2 -30° h 3 + z 1 Contribution to the B matrix z 1 h 0 +

Symmetric laminates •

Symmetric laminates with generally orthotropic plies • Layer Material properties +30° h 3 -60° h 2 15° h 1 -60° h 2 30° h 3 orientation thickness Q 11 Q 12 Q 22 Q 16 Q 26 Q 66 1 F 2 F 3 F 4 F 5 F 6 +30 H 0 2 G 1 G 2 G 3 G 4 G 5 G 6 -60 2 h 0 3 H 1 H 2 H 3 H 4 H 5 H 6 +15 4 h 0 4 G 1 G 2 G 3 G 4 G 5 G 6 -60 2 h 0 5 F 1 F 2 F 3 F 4 F 5 F 6 +30 H 0 Symmetric laminate with five generally orthotropic layers

Regular symmetric angle ply laminates • +30° -30° h +30° -30° +30° Layer Material properties orientation thickness Q 11 Q 12 Q 22 Q 16 Q 26 Q 66 1 F 2 F 3 F 4 F 5 F 6 +30 H 0 2 F 1 F 2 F 3 -F 4 -F 5 F 6 -30 H 0 3 F 1 F 2 F 3 F 4 F 5 F 6 +30 H 0 4 F 1 F 2 F 3 -F 4 -F 5 F 6 -30 H 0 5 F 1 F 2 F 3 F 4 F 5 F 6 +30 H 0 h

Regular symmetric angle ply laminates • Contribution to the A matrix h 0 + h 0 - + Odd term

Regular symmetric angle ply laminates •

Regular symmetric angle ply laminates • Odd term + K=6 K=4 K=2 - + - +

Regular symmetric angle ply laminates •

Elastic properties of a symmetric laminate with general orthotropic plies or angle ply •

Symmetric laminates with isotropic plies • Layer Material properties thickness 1 E 1 , 1 H 0 2 E 2 , 2 2 h 0 3 E 3 , 3 3 h 0 4 E 3 , 3 3 h 0 5 E 2 , 2 2 h 0 6 E 1 , 1 h 0 Symmetric laminate with six multiple isotropic layers E 1 , h E 2 , h E 1 , h

Symmetric laminates with “specially orthotropic plies”- cross-ply • Layer Material properties thickness Q 11 Q 12 Q 22 Q 66 1 F 2 F 3 F 4 H 0 2 F 3 F 2 F 1 F 4 2 h 0 3 F 1 F 2 F 3 F 4 4 h 0 4 F 3 F 2 F 1 F 4 3 h 0 5 F 1 F 2 F 3 F 4 2 h 0 Symmetric laminate orthotropic layers with five specially

Elastic properties of a symmetric cross ply laminate •

Elastic properties of a symmetric angle ply laminate- high number of plies •

Balanced laminates They consist of an even number of adjacent plies with angles of the principal axis of the material of opposite sign (+ and - ) with respect to the midplane of the laminate For each ply above the midplane with an orientation angle , there is a ply below the midplane with the same thickness and orientation angle - , no matter what is the distance from the midplane 30° t 3 60° t 2 -45° t 1 -30° t 3 45° t 1 -60° t 2

Balanced laminates • h 0 + z 1 z 2 h 0 - Contribution to the A 16 and A 26

Antisymmetric balanced laminate • h 0 + z 1 Contribution to D 16 , D 26 z 1 h 0 Layer - Material properties -45° h 3 30° h 2 90° h 1 -30° h 2 45° h 3 angle thickness Q 11 Q 12 Q 22 Q 16 Q 26 Q 66 1 F 2 F 3 -F 4 -F 5 F 6 -45 h 0 2 G 1 G 2 G 3 G 4 G 5 G 6 30 2 h 0 3 H 2 H 1 H 4 H 5 H 6 90 3 h 0 4 H 1 H 2 H 3 H 4 H 5 H 6 0 3 h 0 5 G 1 G 2 G 3 -G 4 -G 5 G 6 -30 2 h 0 6 F 1 F 2 F 3 F 4 F 5 F 6 45 h 0

Antisymmetric laminates cross-ply 0° h 3 90° h 2 90° h 1 0° h 2 90° h 3 Layer Material properties orientation thickness Q 11 Q 12 Q 22 Q 66 1 F 2 F 3 F 4 0 h 0 2 F 3 F 2 F 1 F 4 90 3 h 0 3 F 2 F 1 F 4 90 2 h 0 4 F 1 F 2 F 3 F 4 0 2 h 0 5 F 1 F 2 F 3 F 4 0 3 h 0 6 F 3 F 2 F 1 F 4 90 h 0

Antisymmetric laminates cross-ply

Antisymmetric laminates cross-ply Q 11 Q 22 Z+h 0 Z+2 h 0 z -(Z+2 h 0) Q 11 Q 22

Antisymmetric laminates angle-ply -30° h 3 30° h 2 -30° h 1 -30° h 2 30° h 3 h 0 + z 1 Contribution to the B matrix z 1 h 0 -

Antisymmetric laminates angle-ply + - z. K zk-1 z. K+1

Non symmetric laminates consisting of isotropic plies •

summary laminate Main Subclasses property constraint None Isotropic plies Generally orthotropic plies As N increases A 16=0 A 26=0 D 16=0 D 26=0 None Odd number symmetric B=0 Angle ply Specially orthotropic plies (cross ply) Odd number A 16=0 A 26=0 D 16=0 D 26=0 A 16 0 A 26 0 D 16 0 D 26 0

summary laminate Main Subclasses property balanced A 16=0 A 26=0 Anti. D 16=0 symmetric D 26=0 Angle ply Specially orthotropic plies (cross ply) constraint As N increases Even number B 11=0 B 22=0 B 12=0 B 66=0 B 16 0 B 26 0 Even number B 16=0 B 26=0 B 66=0 B 22=-B 11 0 B 22 0

Dawson, C. , et al. , Nature (1997) 390, 668 Non simmetric laminates ……in nature A sketch of actuation of branches in a pine cone upon (a) wetting and (c) drying A sketch of actuation of branches in a pine cone upon (a) drying and (b) wetting. Each branch can be viewed as a bilayer structure (c, d), made of two unidirectional composite laminate at 0 and 90°. Each branch consists of two types of tissues, one consisting of cells in which the cellulose microfibrils are aligned along the length of the scale and the other in which they are perpendicular. The swelling/shrinking direction in each layer is constrained by the orientation of the stiff cellulose microfibrils in the adjacent layer. The bottom layer (blue) upon shrinking will contract along the length of the branch however, the stiff upper layer will not contract, thus causing the pine cone to open

Quasi-isotropic laminates These laminates have quasi-isotropic extensional stiffness properties The laminate should have more than two layers. N=3 = /3 All layers should have identical stiffness matrices and thicknesses. The difference in orientation angle of two adjacent layers must be equal. Thus, the angle between two adjacent layers should be /N where N is total number of layers in the composite plate. N=4 = /4 It is intuitive that: A 11=A 22 A 66=(A 11 -A 12)/2 A 16=A 26=0 N=5 = /5

Quasi-isotropic laminates Examples: [0, +45, 90, -45]s 45/90/+45/0] (8 plies) [0/+45/90/-45/- N=3 = /3 [0, +45, 90]s [0/+45/-45/90/90/-45/+45/0] (8 plies; very commonly used!) [0, +60]s [0/+60/-60/+60/0] (6 plies and thinner than the formers) However, the Bij and Dij depend on the orientation of the coordinate axis of the laminate. The laminate can have bending-extension coupling as well as different bending response as the laminate is rotated in plane N=4 = /4 N=5 = /5

Stiffness and strenght of a short fiber composite with random fiber orientation In analogy with quasi isotropic laminates, a short fiber composite with random fiber orientation can be considered as a quasi-isotropic laminate with random orientation of many unidirectional laminae. The macromechanics of the laminates is used to obtain a typical result of micromechanics !

Coefficients of thermal expansion • M 22 11 F 0 F 1

Thermoelastic analysis Thermal strains are due to free expansions (or contractions) caused by temperature variations. Thermal loads appear due to restrictions imposed by various layers against their free thermal expansion. In many applications involving polymer matrix composites, moisture can also influence the laminate strains owing to volumetric expansion (swelling) or contraction of the matrix caused by moisture absorption or desorption. In such cases, also the hygroscopic strains should be taken into account. Even if no external loads are applied, that is, if [ N] =[ M]=[0], there may be midplane strains and curvatures due to thermal effects, which in turn will create thermal stresses in various laminas. When a composite laminate is cooled from the curing temperature to room temperature, significant residual stresses may develop owing to thermal mismatch of various laminas. In some cases, these curing stresses may be sufficiently high to cause intralaminar cracks. Therefore, it may be prudent to consider them in the analysis of composite laminates

Thermoelastic analysis •

Thermal curvatures •

Thermal curvatures • Stiffn ess matric es A 142850 4580 142850 0 0 B -62605 0 0 D 47620 1530 47620 0 0 inver se 0 0 6508 0 0 0 2170 A-1 B-1 D-1 7. 01 E-06 -2. 25 E-07 0. 00 E+00 -1. 60 E-05 0. 00 E+00 2. 10 E-05 -6. 75 E-07 0. 00 E+00 -2. 25 E-07 0. 00 E+00 B*A-1 7. 01 E-06 0. 00 E+00 1. 54 E-04 0. 00 E+00 B*A-1*B 1. 60 E-05 0. 00 E+00 -6. 75 E-07 0. 00 E+00 D* 2. 10 E-05 0. 00 E+00 4. 61 E-04 -4. 39 E-01 -1. 41 E-02 0. 00 E+00 2. 75 E+04 8. 81 E+02 0. 00 E+00 2. 02 E+04 6. 49 E+02 0. 00 E+00 1. 41 E-02 4. 39 E-01 0. 00 E+00 8. 81 E+02 2. 75 E+04 0. 00 E+00 6. 49 E+02 2. 02 E+04 0. 00 E+00 D 1 4. 97 E-05 -1. 60 E-06 0. 00 E+00 -1. 60 E-06 4. 97 E-05 0. 00 E+00 4. 61 E-04 0. 00 E+00 D 1*B -3. 11 E+00 -1. 00 E-01 0. 00 E+00 1. 00 E-01 3. 11 E+00 0. 00 E+00 C 1 2. 18 E-05 3. 49 E-09 0. 00 E+00 -3. 49 E-09 -2. 18 E-05 0. 00 E+00 2. 17 E+03 0. 00 E+00

Residual stresses of a symmetric cross-ply • 0 90 90 0 h

Residual stresses of a symmetric cross-ply •