MACROECONOMETRICS LAB 3 DYNAMIC MODELS ROADMAP l What

MACROECONOMETRICS LAB 3 – DYNAMIC MODELS

ROADMAP l What if we know that the effect lasts in time? l Distributed lags l – ALMON – KOYCK – ADAPTIVE EXPECTATIONS – PARTIAL ADJUSTMENT STATA not really too complicated here

How to do lags? l Infinite? – – l how many lags do we take? how to know? Unrestricted? – – – do we impose any structure on the lags? this structure might be untrue? but there is also cost to unrestricted approach. . .

Unrestricted lags (no structure) – It is always finite! yt = + 0 xt + 1 xt-1 + 2 xt-2 +. . . + n xt-n + et l l N lags and no structure in parameters OLS works BUT l l n observations lost high multicollinearity imprecise, large s. e. , low t, lots of d. f. Lost STRUCTURE COULD HELP

Arithmetic lag l l l The effect of X eventually zero Linearly! The coefficients not independent of each other – – effect of each lag less than previous exactly like arithmetic series: un=u 1+d(n-1)

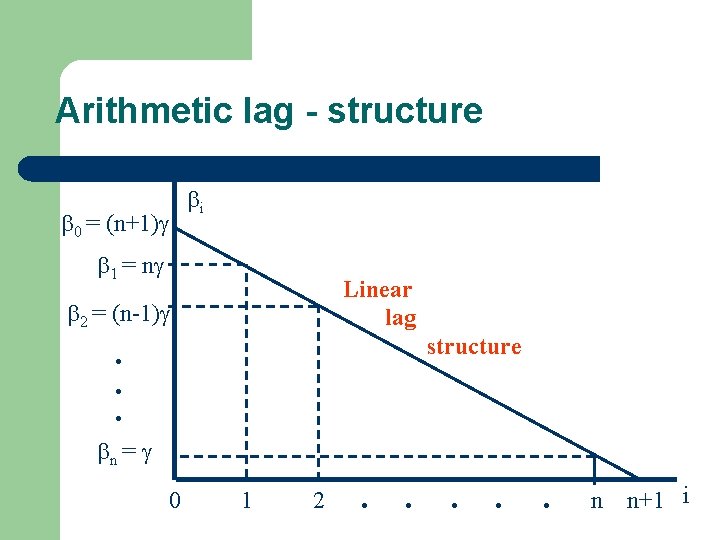
Arithmetic lag - structure i 0 = (n+1) 1 = n Linear lag 2 = (n-1) structure . . . n = 0 1 2 . . . n n+1 i

Arithmetic lag - maths l l l X (log of) money supply and Y (log of) GDP, n=12 and is estimated to be 0. 1 the effect of a change in x on GDP in the current period is =(n+1) =1. 3 the impact of monetary policy one period later has declined to =n =1. 2 n periods later, the impact is n= =0. 1 n+1 periods later the impact is zero

Arithmetic lag - estimation l l OLS, only need to estimate one parameter: STEP 1: impose restriction yt = + 0 xt + 1 xt-1 + 2 xt-2 +. . . + n xt-n + et l STEP 2: factor out the parameter yt = + [(n+1)xt + nxt-1 + (n-1)xt-2 +. . . + xt-n] + et l STEP 3: define z zt = [(n+1)xt + nxt-1 + (n-1)xt-2 +. . . + xt-n] l STEP 4: decide n (no. of lags) For n = 4: ? ? ? zt = [ 5 xt + 4 xt-1 + 3 xt-2 + 2 xt-3 + xt-4]

Arithmetic lag – pros & cons l Advantages: – Only one parameter to be estimated! t-statistics – l Straightforward interpretation Disadvantages: – l ok. , better s. e. , results more reliable If restriction untrue, estimators biased and inconsistent Solution? F-test! (see: end of the notes)

Polynomial lag (ALMON) l If we want a different shape of IRF. . . – – – It’s just a different shape Still finite: the effect eventually goes to zero (by DEFINITION and not by nature!) The coefficients still related to each other BUT not a uniform pattern (decline)

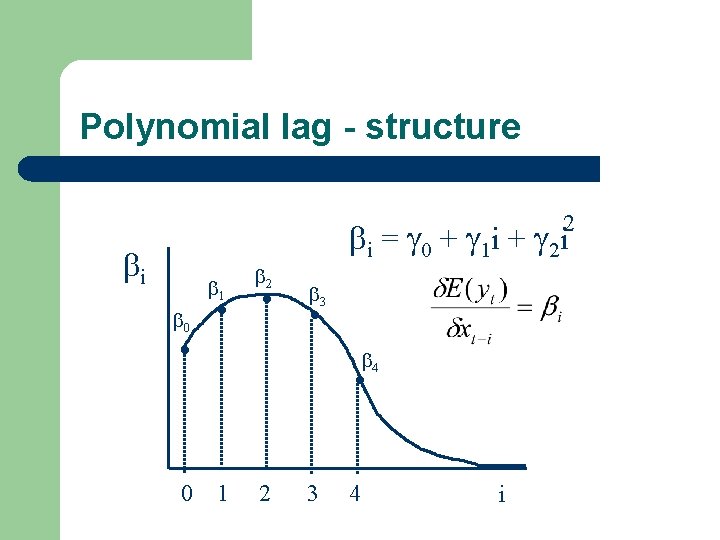
Polynomial lag - structure 2 i . . . 1 0 . 0 i = 0 + 1 i + 2 i 2 3 . 4 1 2 3 4 i

Polynomial lag - maths l l n – the lenght of the lag p – degree of the polynomial i = 0 + 1 i + 2 i 2 +. . . + pip, where i=1, . . . , n l For example a quadratic polynomial i = 0 + 1 i + 2 i 2 , where p=2 0 = 0 2 = 0 + 2 1 + 4 2 4 = 0 + 4 1 + 16 2 and n=4 1 = 0 + 1 + 2 3 = 0 + 3 1 + 9 2

Polynomial lags - estimation l l OLS, only need to estimate p parameters: , . . . , p STEP 1: impose restriction yt = + 0 xt + 0 + 1 + 2 xt-1+( 0 +2 1 +4 2)xt-2+( 0+3 1 +9 2)xt-3+ ( 0 +4 1 + 16 2)xt-4 + et l STEP 2: factor out the unknown coefficients yt = + 0 [xt +xt-1+xt-2+xt-3 +xt-4]+ 1[xt+xt-1+2 xt-2+3 xt-3 +4 xt-4] + 2 [xt + xt-1 + 4 xt-2 + 9 xt-3 + 16 xt-4] + et l STEP 3: define z z t 0 = [xt + xt-1 + xt-2 + xt-3 + xt-4] z t 1 = [xt + xt-1 + 2 xt-2 + 3 xt-3 + 4 xt- 4 ] z t 2 = [xt + xt-1 + 4 xt-2 + 9 xt-3 + 16 xt- 4] l STEP 4: do OLS on yt = + 0 z t 0 + 1 z t 1 + 2 z t 2 + et

Polynomial lag – pros & cons l Advantages: – Fewer parameters to be estimated than in the unrestricted lag structure l – If the polynomial restriction likely to be true: l l More precise than unrestricted More flexible than arithmetic DL Disadvantages If the restriction untrue, biased and inconsistent (see F-test in the end of the notes) –

Arithmetic vs. Polynomial vs. ? ? ? l Conclusion no. 1 – l Conclusion no. 2 – l Data should decide about the assumed pattern of impulseresponse function We still do not know, how many lags! Conclusion no. 3 – We still have a finite no. of lags.

Geometric lag (KOYCK) l l Distributed lag is infinite lag length (no time limits) BUT cannot estimate an infinite number of parameters! Restrict the lag coefficients to follow a pattern l For the geometric lag the pattern is one of continuous decline at decreasing rate (we are still stuck with the problem of imposing fading out instead of observing it – gladly, it is not really painful, as most processes behave like that anyway )

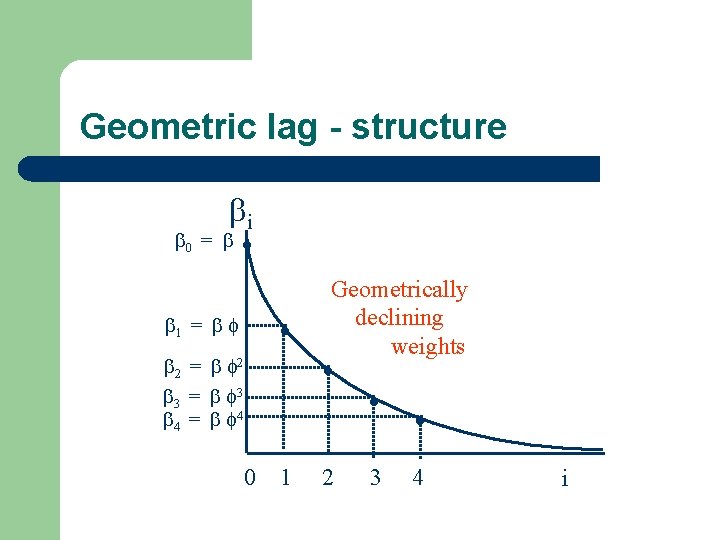
Geometric lag - structure i 0 = . . 1 = 2 = 2 3 = 3 4 = 4 0 1 Geometrically declining weights . 2 . . 3 4 i

Geometric lag - maths l Infinite distributed lag model yt = + 0 xt + 1 xt-1 + 2 xt-2 +. . . + et yt = + i xt-i + et l Geometric lag structure i = i where | | < 1 and i l l Infinite unstructured geometric lag model yt = + 0 xt + 1 xt-1 + 2 xt-2 + 3 xt-3 +. . . + et AND: 0= , 1= , 2= 2, 3= 3. . . Substitute i => infinite geometric lag yt = + xt-1 + xt-2 + xt-3 +. . . ) + et

Geometric lag - estimation l Cannot estimate using OLS yt-1 is dependent on et-1 cannot alow that (need to instrument) l l Apply Koyck transformation Then use 2 SLS Only need to estimate two parameters: , Have to do some algebra to rewrite the model in form that can be estimated.

Geometric lag – Koyck transformation Original equation: yt = + xt-1 + xt-2 + xt-3 +. . . ) + et l Koyck rule: lag everything once, multiply by and substract from the original yt = + xt-1 + xt-2 + xt-3 +. . . ) + et yt-1 = + xt-1 + xt-2 + xt-3 +. . . ) + et-1 l yt yt-1 = + xt + (et et-1) yt = + yt-1 + xt + (et et-1) so yt = + yt-1 + xt + t l l yt-1 is dependent on et-1 so yt-1 is correlated with vt-1 OLS will be consistent (it cannot distinguish between change in yt caused by yt-1 that caused by vt)

Geometric lag - estimation l l l Regress yt-1 on xt-1 and calculate the fitted value Use the fitted value in place of yt-1 in the Koyck regression and that is it! Why does this work? – l from the first stage fitted value is not correlated with et-1 but yt-1 is so fitted value is uncorrelated with vt =(et -et-1 ) 2 SLS will produce consistent estimates of the Geometric Lag Model

Geometric lag – pros & cons l Advantages – l Disadvantages – l You only estimate two parameters! We allow neither for heterogenous nor for unsmooth declining It has many well specified versions, among which two have particular importance: ADAPTIVE EXPECTATIONS – PARTIAL ADJUSTMENT MODEL (for both: see next student presentation) –

F-tests of restrictions 3. Estimate the unrestricted model Estimate the restricted (any lag) model Calculate the test statistic 4. Compare with critical value F(df 1, df 2) 1. 2. l l 5. df 1 = number of restrictions df 2 = number of observations-number of variables in the unrestricted model (incl. constant) H 0: residuals are ‘the same’, restricted model OK