MachinePart Cell Formation Mohammed Fazle Baki Yash Paul

Machine-Part Cell Formation Mohammed Fazle Baki Yash Paul Aneja Guoqing Zhang University of Windsor 1

Overview of Presentation • • Machine-Part Cell Formation Problem Grouping Measures Similarity Coefficients Weight A New Formulation A Special Case Conclusion 2

Machine-Part Cell Formation Problem • Production system – Neither flow shop, nor job shop – Batch production • Part family – All parts in a part family visit a group of similar machines • Similar machines – Visited by a part family 3

Machine-Part Cell Formation Problem • Cell formation problem – Given machine-part incidence matrix – Identify similar parts and similar machines Example 1 4

Machine-Part Cell Formation Problem • Cell formation problem – Rearrange rows and columns – To get diagonal blocks of “ 1” Example 1 5

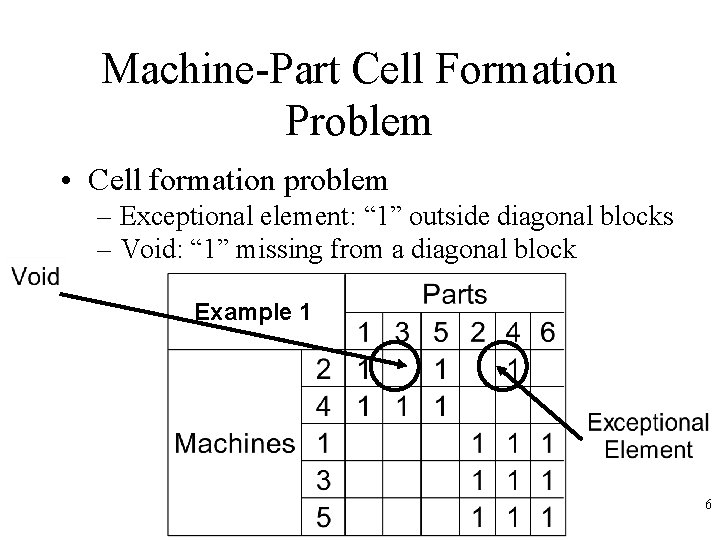
Machine-Part Cell Formation Problem • Cell formation problem – Exceptional element: “ 1” outside diagonal blocks – Void: “ 1” missing from a diagonal block Example 1 6

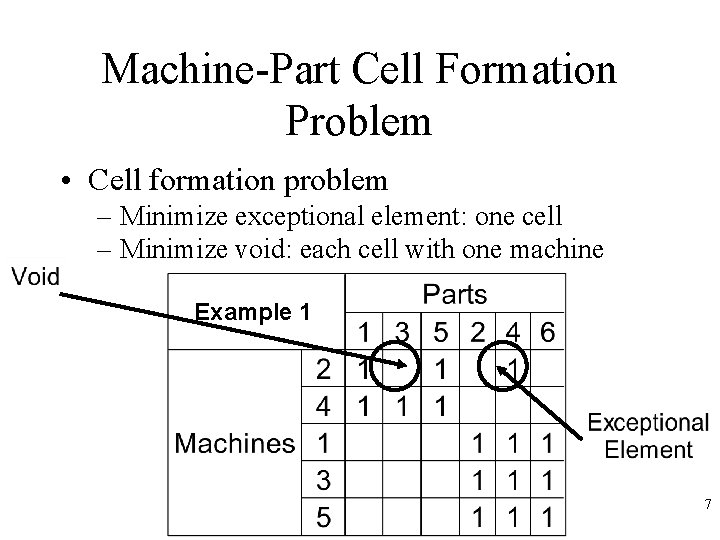
Machine-Part Cell Formation Problem • Cell formation problem – Minimize exceptional element: one cell – Minimize void: each cell with one machine Example 1 7

Grouping Measures A: Number of operations or “ 1”s E: Number of Exceptional elements V: Number of voids m: number of machines n: number of parts q: a weight 8

Grouping Measures A: Number of operations or “ 1”s E: Number of Exceptional elements V: Number of voids Better measure w. r. t. discriminating ability Maximize grouping efficiency/efficacy Minimize exceptional elements and voids 9

Grouping Measures Example 1 10

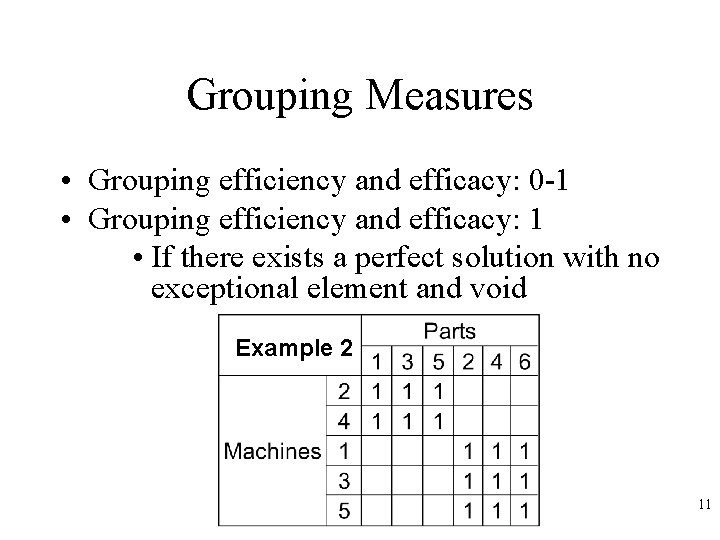
Grouping Measures • Grouping efficiency and efficacy: 0 -1 • Grouping efficiency and efficacy: 1 • If there exists a perfect solution with no exceptional element and void Example 2 11

Similarity Coefficients =1 Example 1 12

Similarity Coefficients =4 Example 1 13

Similarity Coefficients If = 0. 60 = 0. 6(1) + 0. 4(-4) = -1 Example 1 14

Weight • For two machine problems, the following weight guarantees that – If , grouping efficacy is maximized when machines i and j are assigned to the same cell – If , grouping efficacy is maximized when machines i and j are assigned to different cells 15

A Formulation Using Similarity Coefficients 16

A Formulation Using Similarity Coefficients • Example: Machine to machine similarity coefficients Example 1 17

A Formulation Using Similarity Coefficients • Example: Machines 1, 3 and 5 form one cell and Machines 2 and 4 form another cell Example 1 18

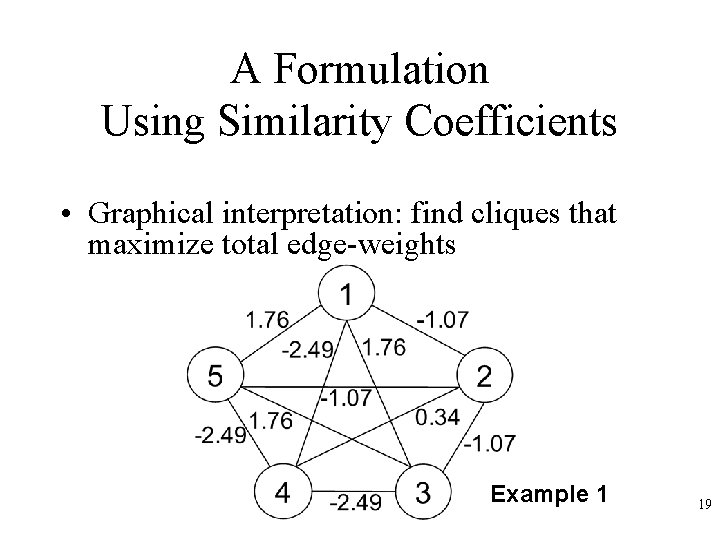
A Formulation Using Similarity Coefficients • Graphical interpretation: find cliques that maximize total edge-weights Example 1 19

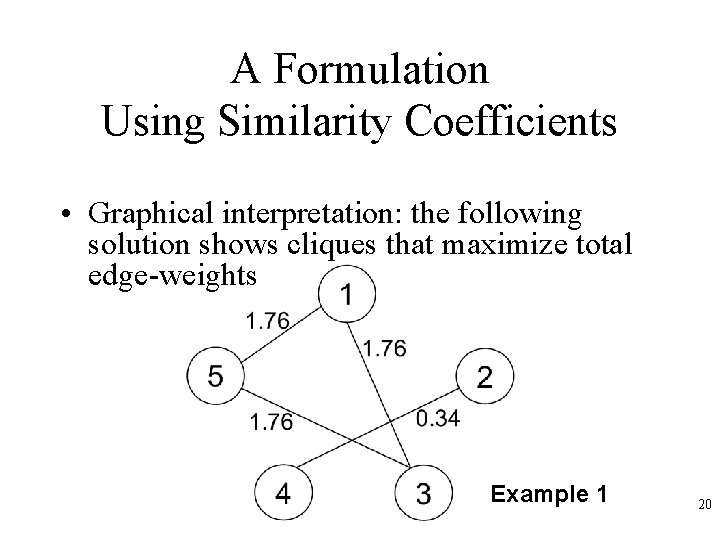
A Formulation Using Similarity Coefficients • Graphical interpretation: the following solution shows cliques that maximize total edge-weights Example 1 20

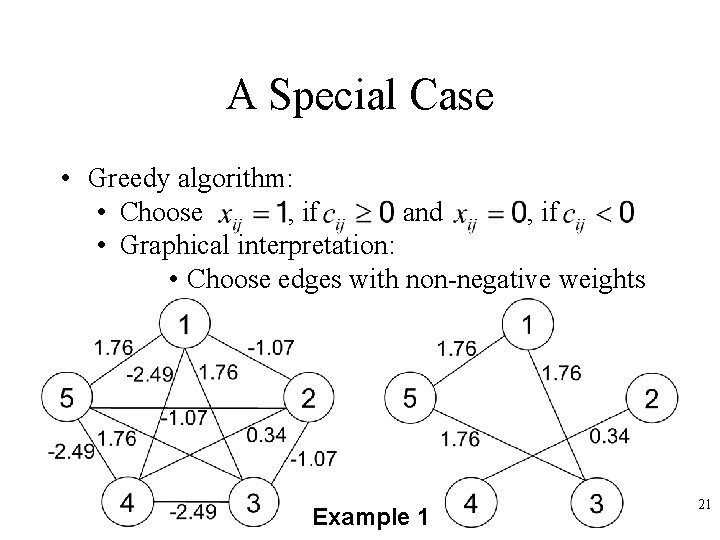
A Special Case • Greedy algorithm: • Choose , if and , if • Graphical interpretation: • Choose edges with non-negative weights Example 1 21

A Special Case • If constraint (3) is relaxed, the greedy algorithm solves the problem in time. • Clique condition: • If the clique condition is satisfied, constraint (3) is redundant A solvable case: If the clique condition is satisfied, the greedy algorithm solves the problem in time 22

A Special Case • If there exists a perfect solution with no element and void, the clique condition is satisfied and the greedy algorithm applies • Example 2 has a perfect solution • The clique condition may be satisfied even when there is no perfect solution • Example 1 satisfies clique condition, but does not have a perfect solution The clique condition is a proper generalization of the case with a perfect solution 23

A Special Case • It can be checked in time if a given instance of the machine-part cell formation problem satisfies the clique condition The clique condition is polynomially testable 24

Conclusion • Machine-part cell formation problem • A new formulation • Using similarity coefficients • Both similarities and dissimilarities • Number of cells is an output, not an input • A special case • Clique condition: generalizes perfect cases • Polynomially solvable • Greedy algorithm: time • Polynomially testable: time 25