Machine Learning Reading Chapter 18 20 Classification Task

Classification Task § Input instance § Tuple of attribute values: <a 1, a 2,

Bayesian Approach § Each observed training example can incrementally decrease or increase probability of

Bayesian Approach § Assign the most probable target value, given <a 1, a 2,

Bayes’ Rules § Product Rule P(a Λ b) = P(a|b)P(b)= P(b|a)P(a) § Bayes’ rule

Naïve Bayes § Assume independence of attributes § P(a 1, a 2, …an|vj)=∏P(ai|vj) i

VNB=argmax P(vj)∏P(ai|vj) vj V S-length S-width P-length Class 1 2 3 high low high

Estimating Probabilities § What happens when the number of data elements is § §

Instead § Use priors as well § nc+mp n+m Where p = prior estimate

KDD Cup § Knowledge Dissemination and Discovery § 2003 – Predicting interest in journal

Slides: 10

Download presentation

Machine Learning Reading: Chapter 18, 20

Classification Task § Input instance § Tuple of attribute values: <a 1, a 2, …an> § Output class § Any value vi from finite set V § Given a training set of instances, predict class of new instance 2

Bayesian Approach § Each observed training example can incrementally decrease or increase probability of hypothesis instead of eliminate an hypothesis § Prior knowledge can be combined with observed data to determine hypothesis § Bayesian methods can accommodate hypotheses that make probabilistic predictions § New instances can be classified by combining the predictions of multiple hypotheses, weighted by their probabilities 3

Bayesian Approach § Assign the most probable target value, given <a 1, a 2, …an> § VMAP=argmax P(vj| a 1, a 2, …an) § Using Bayes Theorem: § VMAP=argmax P(a 1, a 2, …an|vj)P(vi) vj V P(a 1, a 2, …an) =argmax P(a 1, a 2, …an|vj)P(vi) vj V § Bayesian learning is optimal § Easy to estimate P(vi) by counting in training data § Estimating the different P(a 1, a 2, …an|vj) not feasible 4

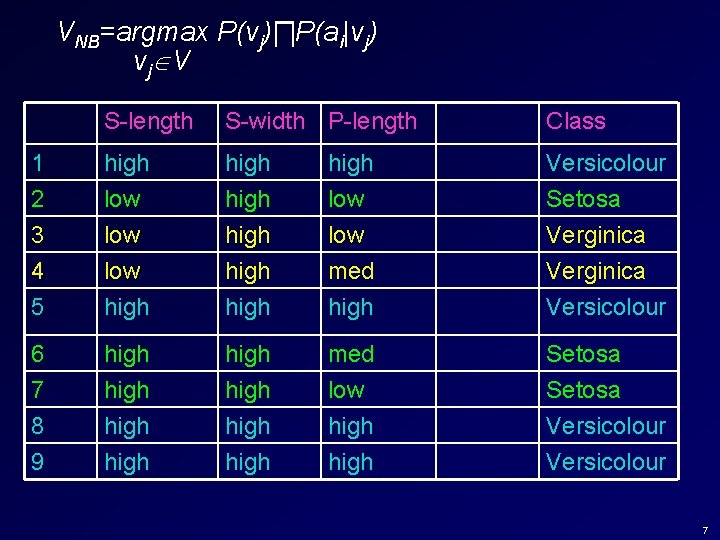
Naïve Bayes § Assume independence of attributes § P(a 1, a 2, …an|vj)=∏P(ai|vj) i § Substitute into VMAP formula § VNB=argmax P(vj)∏P(ai|vj) vj V i 6

VNB=argmax P(vj)∏P(ai|vj) vj V S-length S-width P-length Class 1 2 3 high low high low Versicolour Setosa Verginica 4 5 low high med high Verginica Versicolour 6 7 8 9 high high med low high Setosa Versicolour 7

Estimating Probabilities § What happens when the number of data elements is § § § small? Suppose true P(S-length=low|verginica)=. 05 There are only 2 instances with C=Verginica We estimate probability by nc/n or #Slength|Verginica/C-Verginica #S-length|Verginica must = 0 Then, instead of. 05 we use estimated probability of 0 Two problems § Biased underestimate of probability § This probability term will dominate if future query contains Slength=low 8

Instead § Use priors as well § nc+mp n+m Where p = prior estimate u M is a constant called the equivalent sample size u Determines how heavily to weight p relative to observed data u Typical method: assume a uniform prior u 9

KDD Cup § Knowledge Dissemination and Discovery § 2003 – Predicting interest in journal papers –SVMs a winner § 2002 – Bioinformatics - e. g. , given a set of bioinformatics papers and a § § § list of genes mentioned in each paper, determine for each gene whether the paper has full experimental evidence 2001 – Bioinformatics – prediction of biomolecular activity for drug design; prediction of gene/protein function and localization 2000 – Predicting user activity in online product web site (legwear) 1999 – Network intrusion detection. Given 5 million connection records, predict normal vs. attack (denial of service, remote unauthorized access, local unauthorized access, probing) 1998 – Predict who will give how much to a specific charity based on a variety of demographics 1997 - Two of the 3 winners used Naïve Bayes classifiers 10