Machine Learning Neural Networks 2 Accuracy Easily the

Machine Learning Neural Networks (2)

Accuracy • Easily the most common and intuitive measure of classification performance.

Loss/Error Functions • • • How do we measure performance? Regression: – L 2 error Classification: – #misclassifications – Weighted misclassification via a cost matrix – For 2 -classification: • True Positive, False Positive, True Negative, False Negative – For k-classification: • Confusion Matrix

F-Measure True Values Hyp Values Positive Negative Positive 10 50 Negative 0 40

Types of Errors • False Positives – The system predicted TRUE but the value was FALSE – aka “False Alarms” or Type I error • False Negatives – The system predicted FALSE but the value was TRUE – aka “Misses” or Type II error

Basic Evaluation • • Training data – used to identify model parameters Testing data – used for evaluation Optionally: Development / tuning data – used to identify model hyperparameters. Difficult to get significance or confidence values

Cross validation • • • Identify n “folds” of the available data. Train on n-1 folds Test on the remaining fold. • In the extreme (n=N) this is known as “leave-one-out” cross validation • n-fold cross validation (xval) gives n samples of the performance of the classifier.

Cross-validation visualized Available Labeled Data Identify n partitions Fold 1 Train Dev Test 8

Cross-validation visualized Available Labeled Data Identify n partitions Fold 2 Test Train Dev 9

Cross-validation visualized Available Labeled Data Identify n partitions Fold 3 Dev Test Train 10

Cross-validation visualized Available Labeled Data Identify n partitions Fold 4 Train Dev Test Train 11

Cross-validation visualized Available Labeled Data Identify n partitions Fold 5 Train Dev Test Train 12

Cross-validation visualized Available Labeled Data Identify n partitions Fold 6 Train Dev Test Train Calculate Average Performance 13

Concepts • Capacity – Measure how large hypothesis class H is. – Are all functions allowed? • Overfitting – f works well on training data – Works poorly on test data • Generalization – The ability to achieve low error on new test data

Multi-layers Network • • Let the network of 3 layers – Input layer – Hidden layer – Output layer Each layer has different number of neurons The famous example to need the multi-layer network is XOR unction The perceptron learning rule can not be applied to multi-layer network • We use Back. Propagation Algorithm in learning

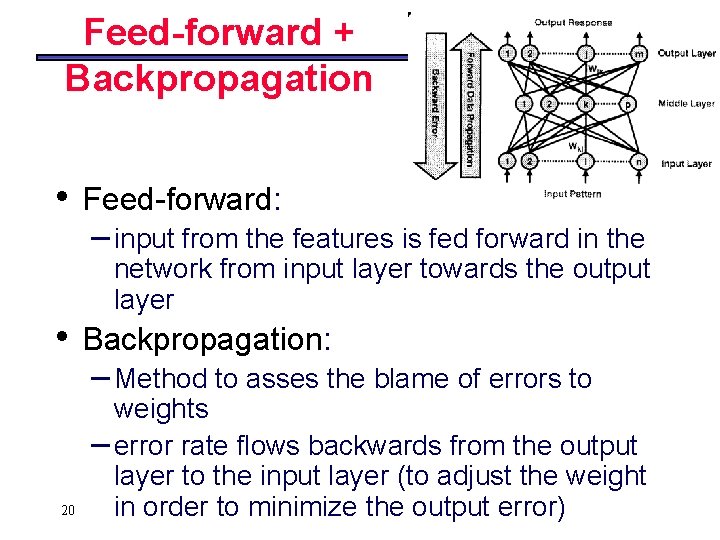
Feed-forward + Backpropagation • • 20 Feed-forward: – input from the features is fed forward in the network from input layer towards the output layer Backpropagation: – Method to asses the blame of errors to weights – error rate flows backwards from the output layer to the input layer (to adjust the weight in order to minimize the output error)

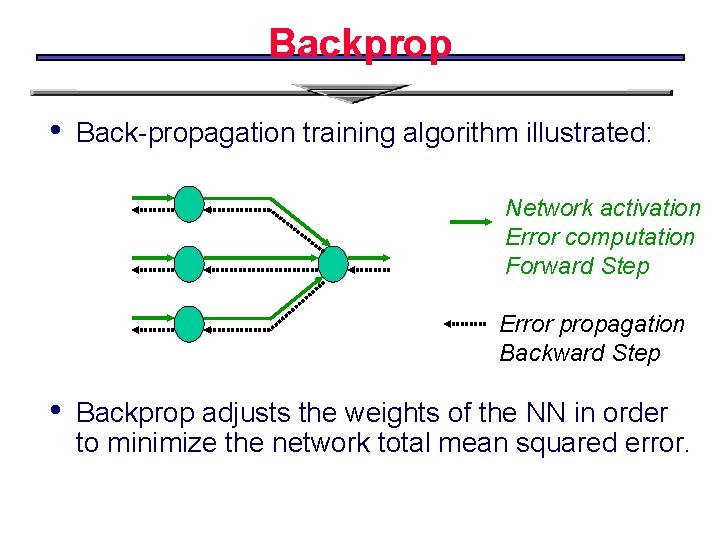
Backprop • Back-propagation training algorithm illustrated: Network activation Error computation Forward Step Error propagation Backward Step • Backprop adjusts the weights of the NN in order to minimize the network total mean squared error.

Correlation Learning Hebbian Learning (1949): “When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes place in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased. ” Weight modification rule: wi, j = c xi xj Eventually, the connection strength will reflect the correlation between the neurons’ outputs.

Backpropagation Learning the goal of the Backpropagation learning algorithm is to modify the network’s weights so that its output vector op = (op, 1, op, 2, …, op, K) is as close as possible to the desired output vector dp = (dp, 1, dp, 2, …, dp, K) for K output neurons and input patterns p = 1, …, P. The set of input-output pairs (exemplars) {(xp, dp) | p = 1, …, P} constitutes the training set. 23

Bp Algorithm • The weight change rule is • Where is the learning factor <1 • Error is the difference between actual and trained value • f’ is is the derivative of sigmoid function = f(1 -f)

Delta Rule • • Each observation contributes a variable amount to the output The scale of the contribution depends on the input Output errors can be blamed on the weights A least mean square (LSM) error function can be defined (ideally it should be zero) E = ½ (t – y)2

Example • For the network with one neuron in input layer and one neuron in hidden layer the following values are given X=1, w 1 =1, b 1=-2, w 2=1, b 2 =1, =1 and t=1 Where X is the input value W 1 is the weight connect input to hidden W 2 is the weight connect hidden to output B 1 and b 2 are bias T is the training value

Exercises • Design a neural network to recognize the problem of • X 1=[2 2] , t 1=0 • X=[1 -2], t 2=1 • X 3=[-2 2], t 3=0 • X 4=[-1 1], t 4=1 Start with initial weights w=[0 0] and bias =0

Exercises • • • Perform one iteration of backprpgation to network of two layers. First layer has one neuron with weight 1 and bias – 2. The transfer function in first layer is f=n 2 The second layer has only one neuron with weight 1 and bias 1. The f in second layer is 1/n. The input to the network is x=1 and t=1

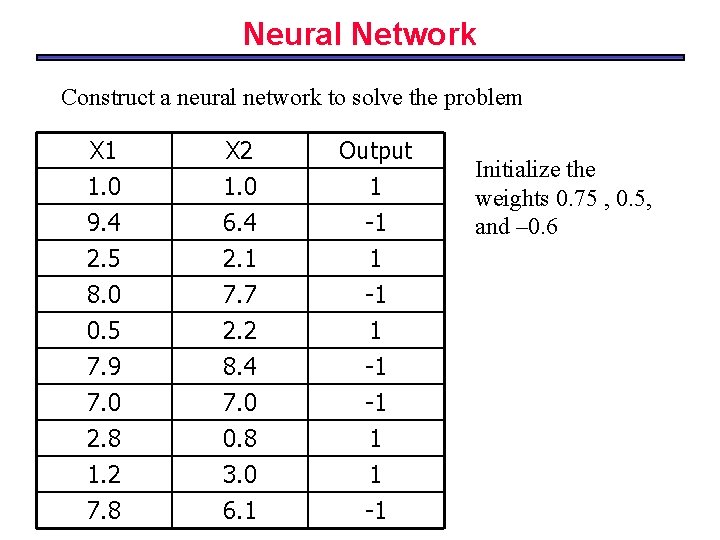
Neural Network Construct a neural network to solve the problem X 1 1. 0 9. 4 2. 5 X 2 1. 0 6. 4 2. 1 Output 1 -1 1 8. 0 0. 5 7. 9 7. 0 2. 8 1. 2 7. 7 2. 2 8. 4 7. 0 0. 8 3. 0 -1 1 -1 -1 1 1 7. 8 6. 1 -1 Initialize the weights 0. 75 , 0. 5, and – 0. 6

Neural Network Construct a neural network to solve the XOR problem X 1 1 0 1 X 2 1 0 0 Output 0 0 1 1 Initialize the weights – 7. 0 , -7. 0, -5. 0 and – 4. 0

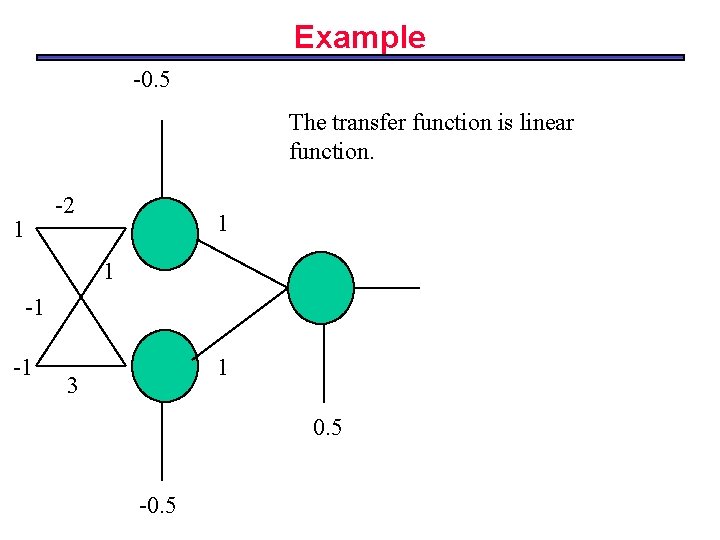
Example -0. 5 The transfer function is linear function. -2 1 1 1 -1 -1 1 3 0. 5 -0. 5

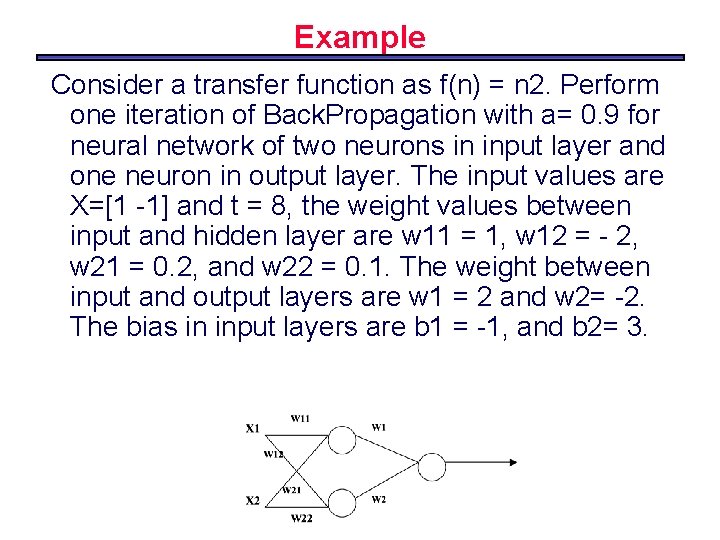
Example Consider a transfer function as f(n) = n 2. Perform one iteration of Back. Propagation with a= 0. 9 for neural network of two neurons in input layer and one neuron in output layer. The input values are X=[1 -1] and t = 8, the weight values between input and hidden layer are w 11 = 1, w 12 = - 2, w 21 = 0. 2, and w 22 = 0. 1. The weight between input and output layers are w 1 = 2 and w 2= -2. The bias in input layers are b 1 = -1, and b 2= 3.

Some variations • • learning rate ( ). If is too small then learning is very slow. If large, then the system's learning may never converge. Some of the possible solutions to this problem are: – Add a momentum term to allow a large learning rate. – Use a different activation function – Use a different error function – Use an adaptive learning rate – Use a good weight initialization procedure. – Use a different minimization procedure 33

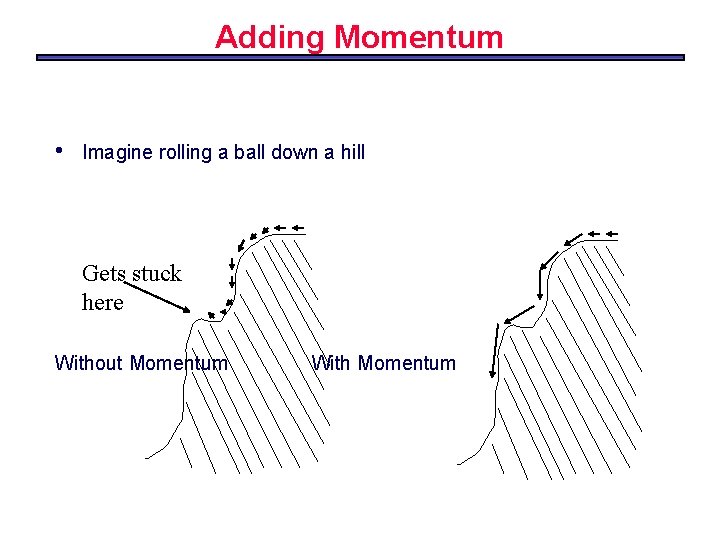
Problems with Local Minima • backpropagation –Can find its ways into local minima • One partial solution: –Random re-start: learn lots of networks • Starting with different random weight settings –Can take best network –Or can set up a “committee” of networks to categorise examples • Another partial solution: Momentum

Adding Momentum • Imagine rolling a ball down a hill Gets stuck here Without Momentum With Momentum

Momentum in Backpropagation • • • For each weight –Remember what was added in the previous epoch In the current epoch –Add on a small amount of the previous Δ The amount is determined by –The momentum parameter, denoted α –α is taken to be between 0 and 1

Momentum • Weight update becomes: • wij (n+1) = ( pj opi) + wij(n) The momentum parameter is chosen between 0 and 1, typically 0. 9. This allows one to use higher learning rates. The momentum term filters out high frequency oscillations on the error surface. 37

Problems with Overfitting • Plot training example error versus test example error: • Test set error is increasing! – – – Network is overfitting the data Learning idiosyncrasies in data, not general principles Big problem in Machine Learning (ANNs in particular)

Avoiding Overfitting • • Bad idea to use training set accuracy to terminate One alternative: Use a validation set – Hold back some of the training set during training – Like a miniature test set (not used to train weights at all) – If the validation set error stops decreasing, but the training set error continues decreasing • Then it’s likely that overfitting has started to occur, so • stop Another alternative: use a weight decay factor – Take a small amount off every weight after each epoch – Networks with smaller weights aren’t as highly fine tuned (overfit)

Feedback NN Recurrent Neural Networks

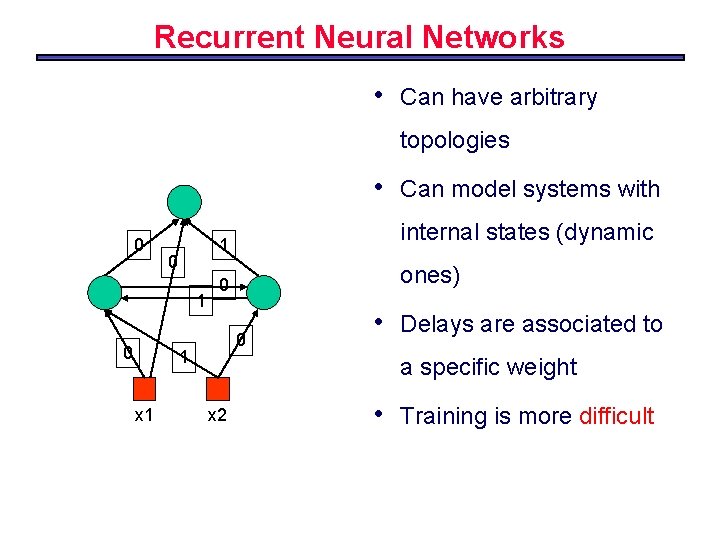
Recurrent Neural Networks • Can have arbitrary topologies • 0 1 0 ones) 0 0 1 x 1 internal states (dynamic 1 0 Can model systems with • Delays are associated to a specific weight x 2 • Training is more difficult

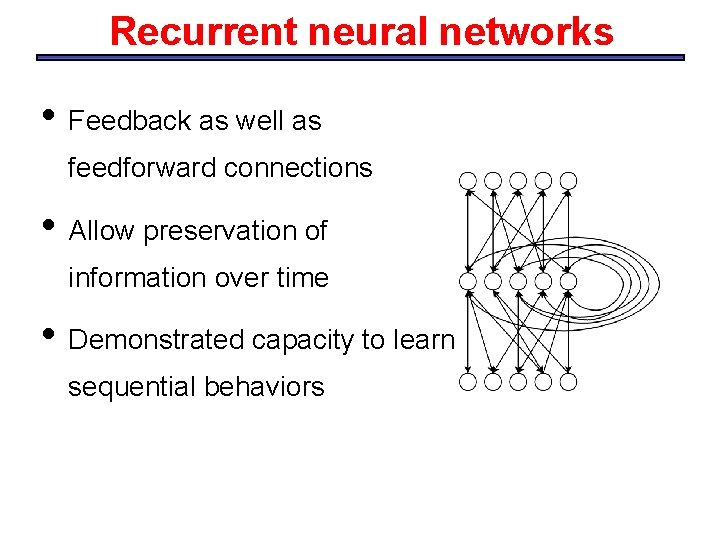
Recurrent neural networks • Feedback as well as feedforward connections • Allow preservation of information over time • Demonstrated capacity to learn sequential behaviors

Recurrent neural networks • Architectures – – • Dynamics of recurrent networks – – • • 43 Totally recurrent networks Partially recurrent networks Continuous time dynamics Discrete time dynamics Associative memories Solving optimization problems

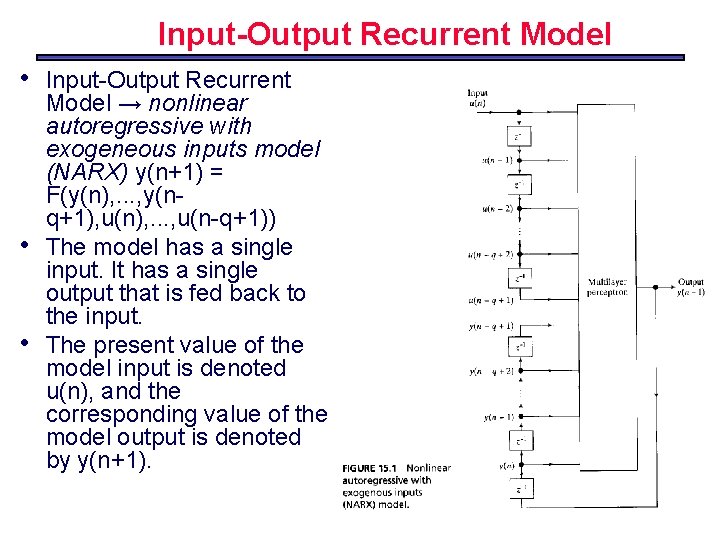
Input-Output Recurrent Model • • • Input-Output Recurrent Model → nonlinear autoregressive with exogeneous inputs model (NARX) y(n+1) = F(y(n), . . . , y(nq+1), u(n), . . . , u(n-q+1)) The model has a single input. It has a single output that is fed back to the input. The present value of the model input is denoted u(n), and the corresponding value of the model output is denoted by y(n+1).

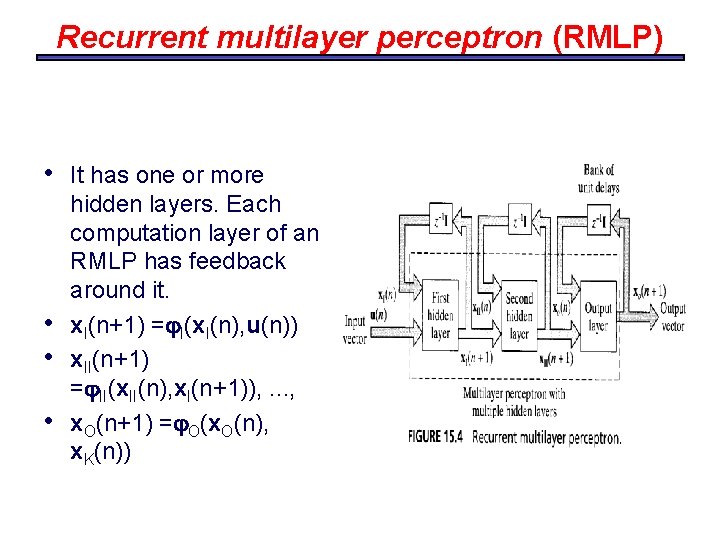
Recurrent multilayer perceptron (RMLP) • • It has one or more hidden layers. Each computation layer of an RMLP has feedback around it. x. I(n+1) = I(x. I(n), u(n)) x. II(n+1) = II(x. II(n), x. I(n+1)), . . . , x. O(n+1) = O(x. O(n), x. K(n))

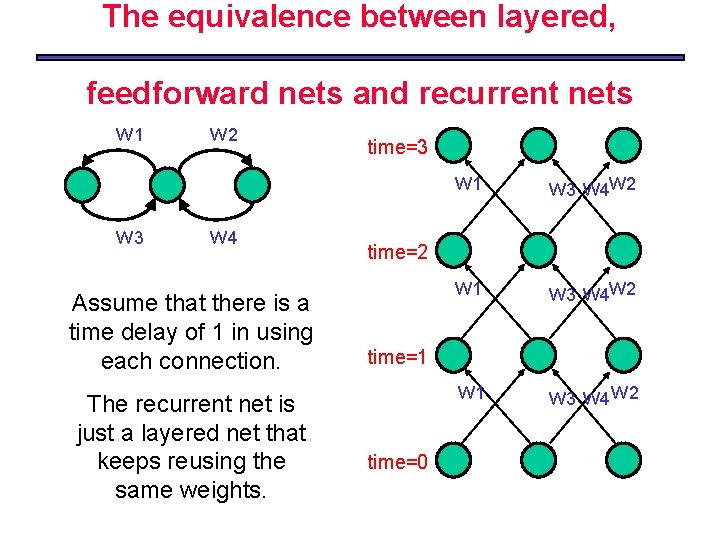
The equivalence between layered, feedforward nets and recurrent nets w 1 w 3 w 2 w 4 Assume that there is a time delay of 1 in using each connection. The recurrent net is just a layered net that keeps reusing the same weights. time=3 w 1 w 3 w 4 w 2 w 1 w 3 w 4 w 2 time=1 time=0

Recurrent Neural Networks : Hopfield Network • • • Proper when exact binary representations are possible. Can be used as an associative memory or to solve optimization problems. The number of classes (M) must be kept smaller than 0. 15 times the number of nodes (N).

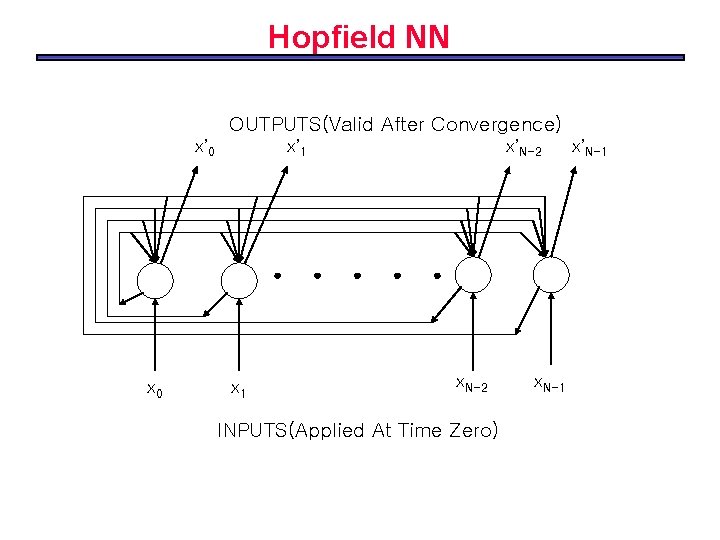
Hopfield NN OUTPUTS(Valid After Convergence) x’ 0 x’ 1 x’N-2 . . . x 0 x 1 x. N-2 INPUTS(Applied At Time Zero) x. N-1 x’N-1

Recurrent Neural Networks : Hopfield Network Algorithm • Step 1 : Assign Connection Weights. • Step 2 : Initialize with unknown input pattern.

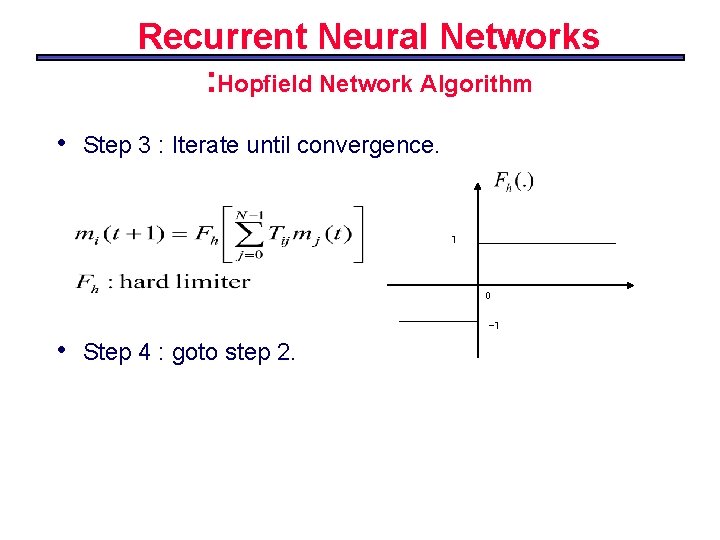
Recurrent Neural Networks : Hopfield Network Algorithm • Step 3 : Iterate until convergence. 1 0 -1 • Step 4 : goto step 2.

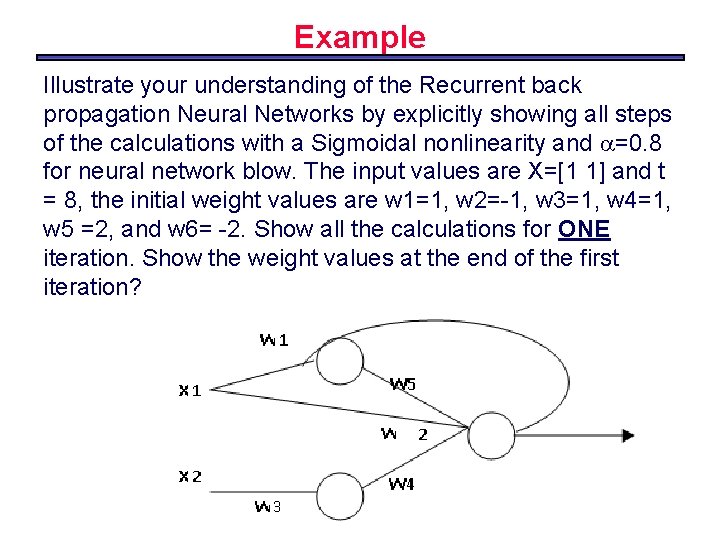
Example Illustrate your understanding of the Recurrent back propagation Neural Networks by explicitly showing all steps of the calculations with a Sigmoidal nonlinearity and =0. 8 for neural network blow. The input values are X=[1 1] and t = 8, the initial weight values are w 1=1, w 2=-1, w 3=1, w 4=1, w 5 =2, and w 6= -2. Show all the calculations for ONE iteration. Show the weight values at the end of the first iteration?

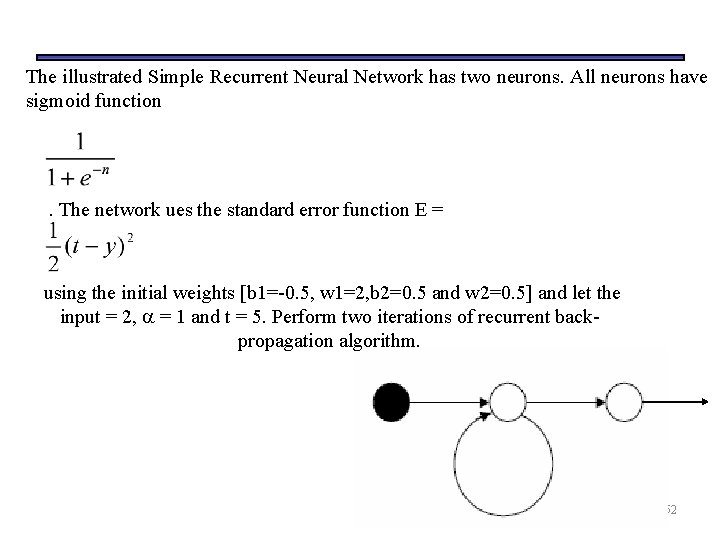
The illustrated Simple Recurrent Neural Network has two neurons. All neurons have sigmoid function . The network ues the standard error function E = using the initial weights [b 1=-0. 5, w 1=2, b 2=0. 5 and w 2=0. 5] and let the input = 2, = 1 and t = 5. Perform two iterations of recurrent backpropagation algorithm. 52