Machine Learning Linear Regression Wilson Mckerrow Fenyo lab

Machine Learning – (Linear) Regression Wilson Mckerrow (Fenyo lab postdoc) Contact: Wilson. Mc. Kerrow@nyumc. org

Linear Regression – one independent variable 2 Data: Predictor Independent Response Dependent Want: (residual) is “small” 2

Linear Regression – one independent variable 3 What is “small”? • Define a loss function: To measure how far off the model is. Want: 3

Linear Regression – one independent variable 4 Standard choice: Sum of square errors (least squares) 4

Linear Regression – one independent variable 5 5

Linear Regression – one independent variable 6 Advantages of least squares: • Gauss-Markov theorem: Lowest variance among unbiased methods. • Equivalent to MLE for 6

Linear Regression – one independent variable 7 Advantages of least squares: • Gauss-Markov theorem: Lowest variance among unbiased methods. • Equivalent to MLE for • Easy to calculate 7

Linear Regression – one independent variable 8 Disadvantages of least squares: • Variance can still be large • Pays attention to outliers 8

Linear Regression – One Independent Variable 9 Minimizing the loss function, L (sum of squared errors): 9

Linear Regression – One Independent Variable 10 Minimizing the loss function, L (sum of squared errors): 10

Linear Regression – Vector notation 11 11

Linear Regression - Multiple Independent Variables 12 12

Linear Regression – Matrix notation 13 13

Linear Regression – Matrix notation 14 Row by column 14

Multiple Linear Regression Minimizing the loss function, L (sum of squared errors): 15

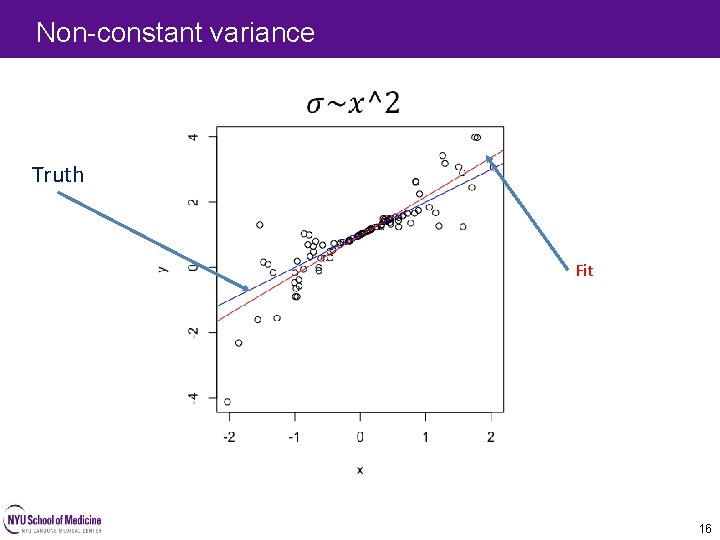
Non-constant variance Truth Fit 16

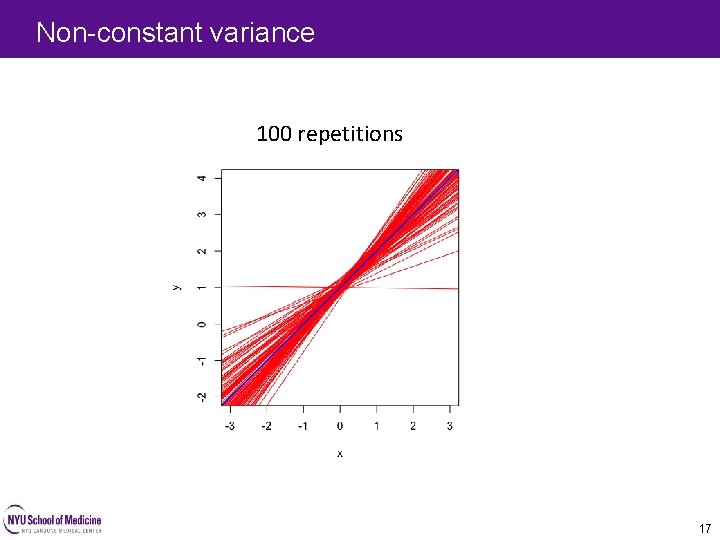
Non-constant variance 100 repetitions 17

Weighted least squares 18

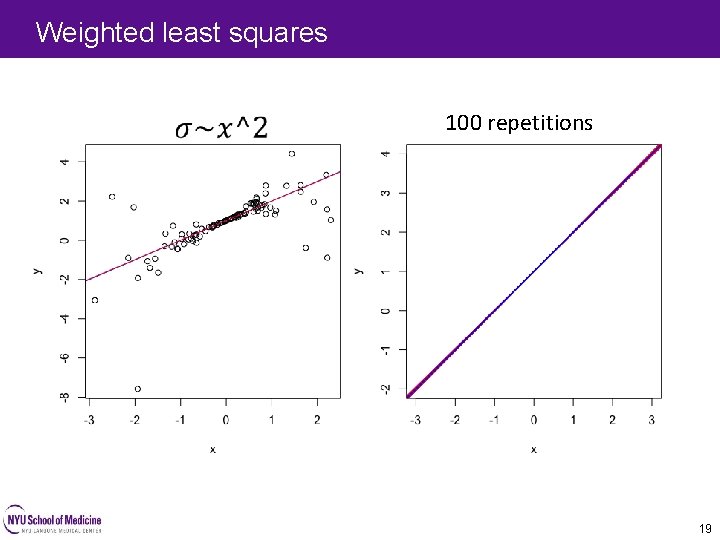
Weighted least squares 100 repetitions 19

(Non)Linear Regression – Sum of Functions 20 20

(Non)Linear Regression – Polynomial 21 21

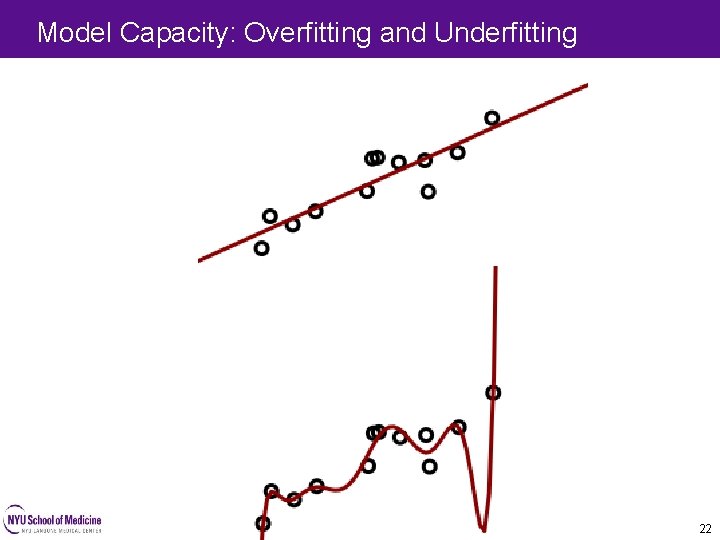
Model Capacity: Overfitting and Underfitting 22 22

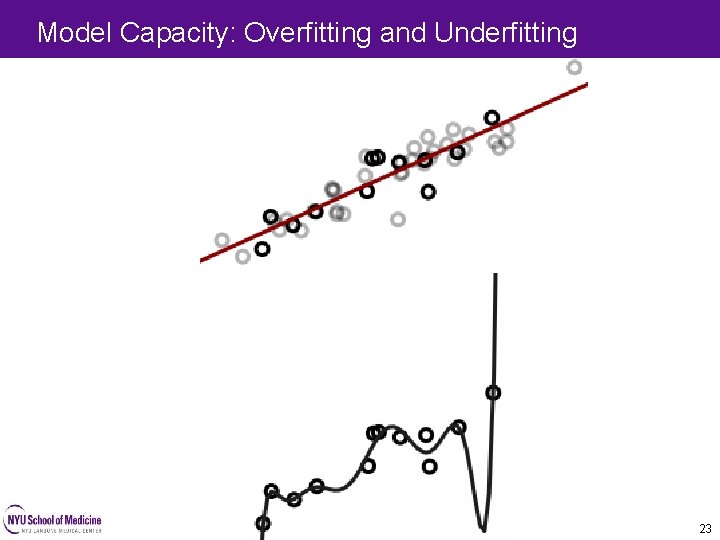
Model Capacity: Overfitting and Underfitting 23 23

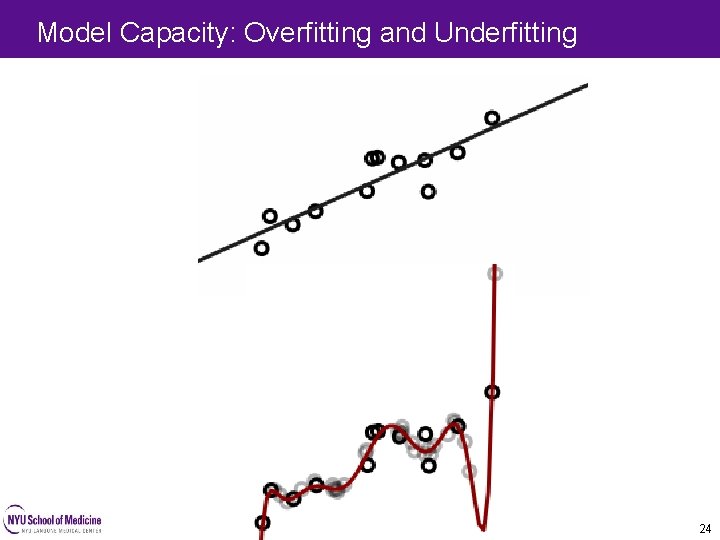
Model Capacity: Overfitting and Underfitting 24 24

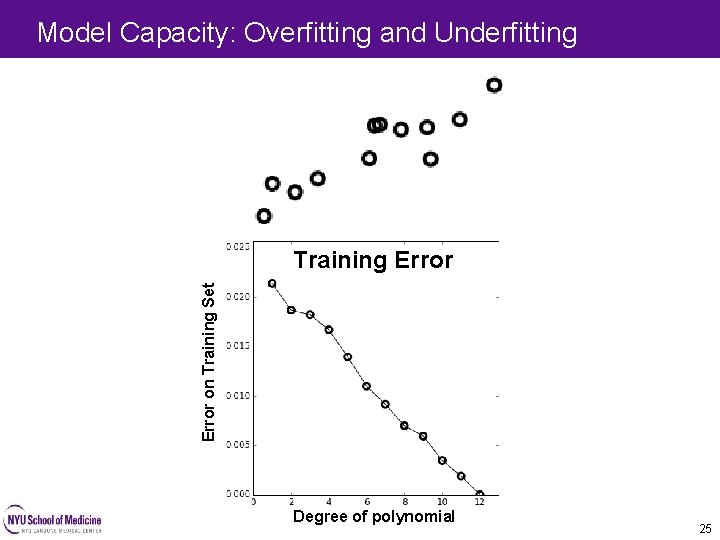
Model Capacity: Overfitting and Underfitting 25 Error on Training Set Training Error Degree of polynomial 25

Model Capacity: Overfitting and Underfitting 26 With four parameters I can fit an elephant, and with five I can make him wiggle his trunk. John von Neumann 26

Training and Testing Data Set Test Training 27

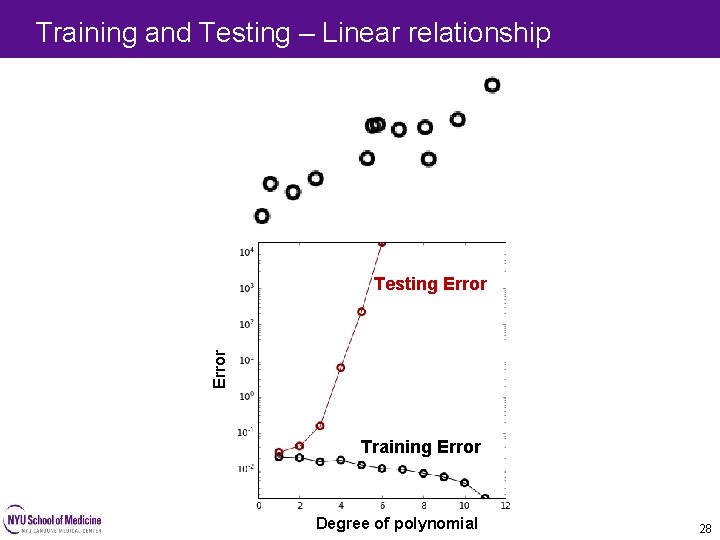
Training and Testing – Linear relationship Error Testing Error Training Error Degree of polynomial 28

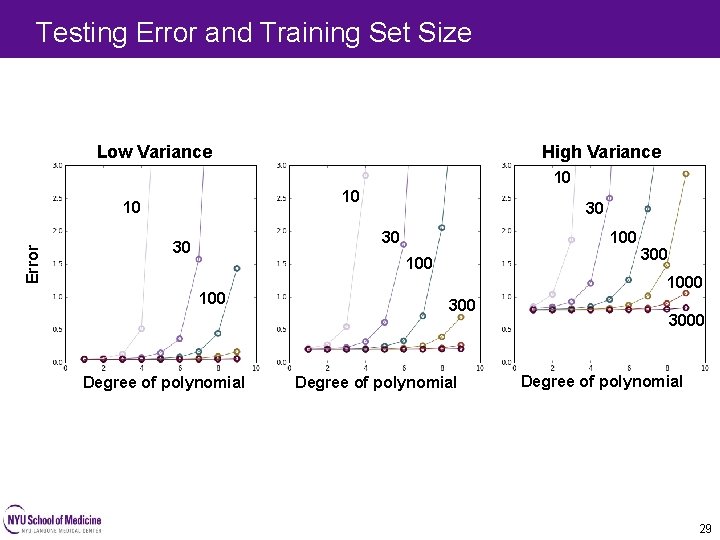
Testing Error and Training Set Size Low Variance High Variance 10 10 Error 10 30 100 30 30 100 Degree of polynomial 300 1000 300 Degree of polynomial 3000 Degree of polynomial 29

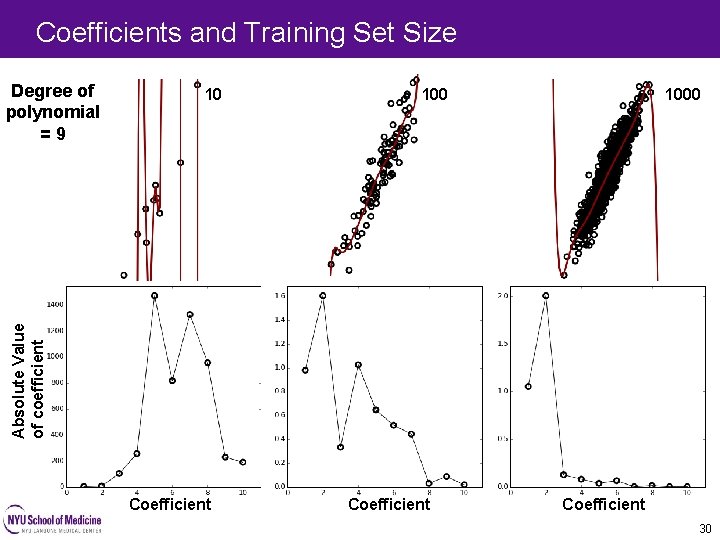
Coefficients and Training Set Size 10 1000 Absolute Value of coefficient Degree of polynomial =9 Coefficient 30

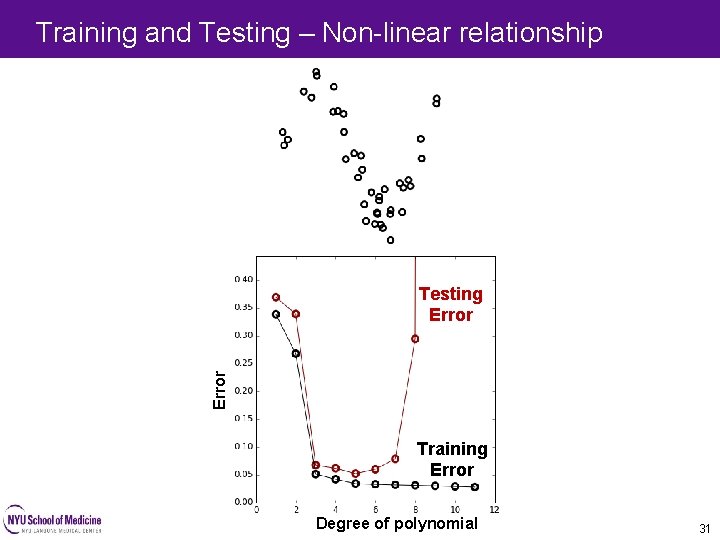
Training and Testing – Non-linear relationship Error Testing Error Training Error Degree of polynomial 31

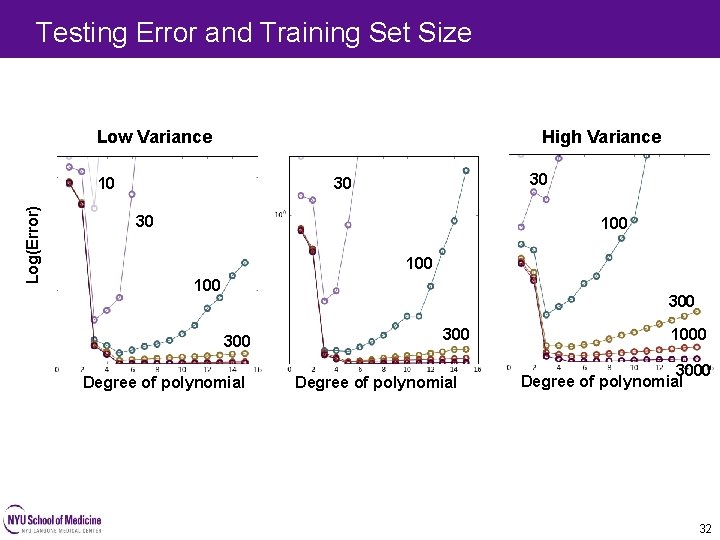
Testing Error and Training Set Size Low Variance High Variance Log(Error) 10 30 30 30 100 100 300 Degree of polynomial 1000 3000 Degree of polynomial 32

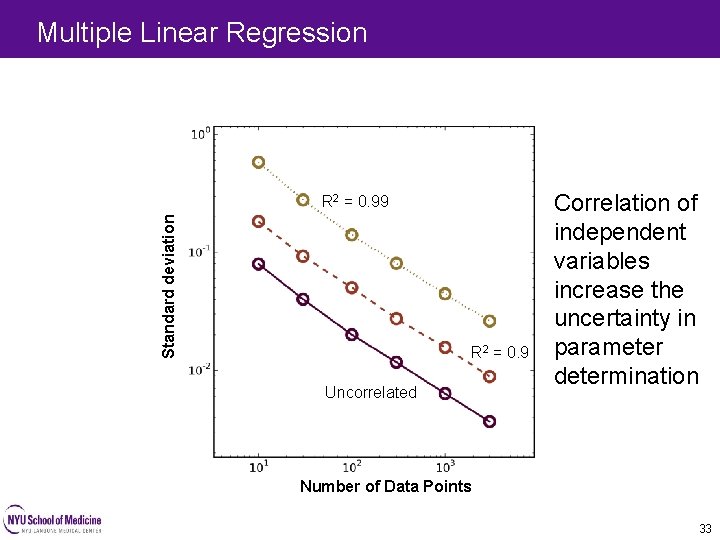
Multiple Linear Regression Standard deviation R 2 = 0. 99 R 2 = 0. 9 Uncorrelated Correlation of independent variables increase the uncertainty in parameter determination Number of Data Points 33

Regularization No Regularization: Ridge Regression: 34

Ridge Regression Recall: 35

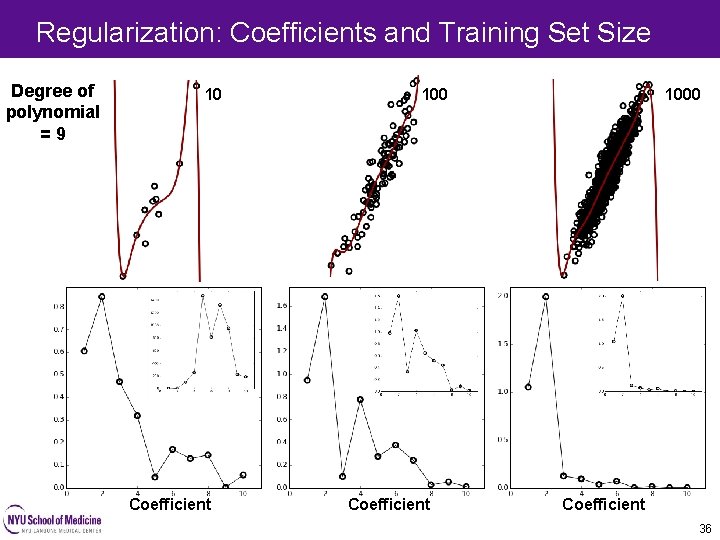
Regularization: Coefficients and Training Set Size Degree of polynomial =9 10 Coefficient 1000 Coefficient 36

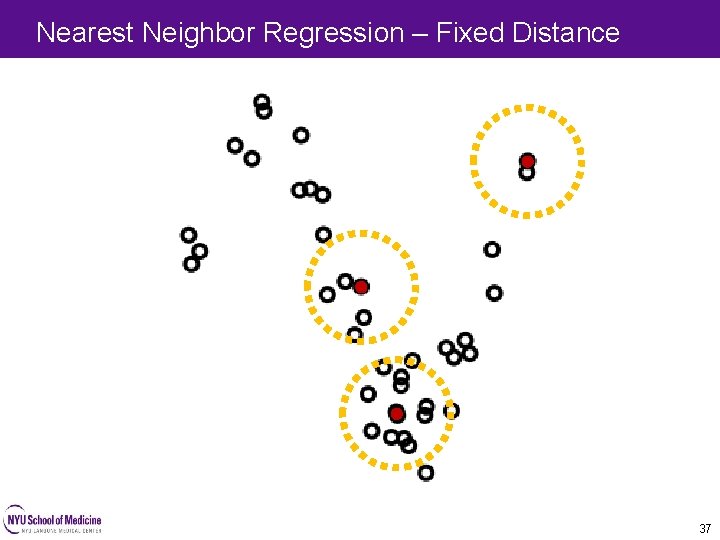
Nearest Neighbor Regression – Fixed Distance 37

Nearest Neighbor Regression – Fixed Number (k. NN) 38

Nearest Neighbor Regression Estimate by taking the average over NNs Or use a distance weighted average 39

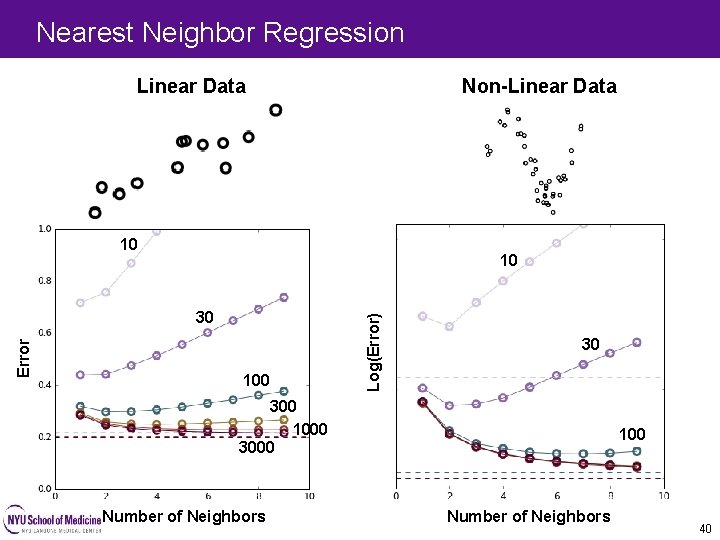
Nearest Neighbor Regression Linear Data Non-Linear Data 10 Error 30 100 Log(Error) 10 30 300 1000 3000 Number of Neighbors 100 Number of Neighbors 40

Questions?