Machine Learning Learning n Definition n Learning is

Machine Learning 참고 자료

Learning n Definition n Learning is the improvement of performance in some environment through the acquisition of knowledge resulting from experience in that environment. 2

Machine Learning: Tasks n Supervised Learning n n Learn fw from training set D={(x, y)} s. t. Classification: y is discrete Regression: y is continuous Unsupervised Learning n n n Learn fw from D={(x)} s. t. Density Estimation Compression, Clustering 3

Machine Learning: Methods n Symbolic Learning n n Neural Learning n n Genetic Algorithms Probabilistic Learning n n Multilayer Perceptrons (MLPs) Evolutionary Learning n n Version Space Learning Bayesian Networks (BNs) Other Machine Learning Methods n Decision Trees (DTs) 4

Applications of Machine Learning n Driving an autonomous vehicle n n Classifying new astronomical structures n n 무인 자동차 운전, 센서기반 제어 등에도 응용 천체 물체 분류, Decision tree learning 기법 사용 Playing world-class Backgammon n 실제 게임을 통해서 전략을 학습, 탐색공간 문제에 응용 5

A Definition of Learning : Well-posed Learning Problems n Definition n n A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E. A class of tasks T Experience E Performance measure P 6

Checkers Problem (2/2) n homepage n n http: //www. geocities. com/Heartland/7134/Green/grprechecker. htm http: //www. acfcheckers. com 8

A Checkers Learning Problem n Three Features: 학습문제의 정의 n n The class of tasks The measure of performance to be improved The source of experience Example n n n Task T: playing checkers Performance measure P: percent of games won against opponent Training experience E: playing practice games against itself 9

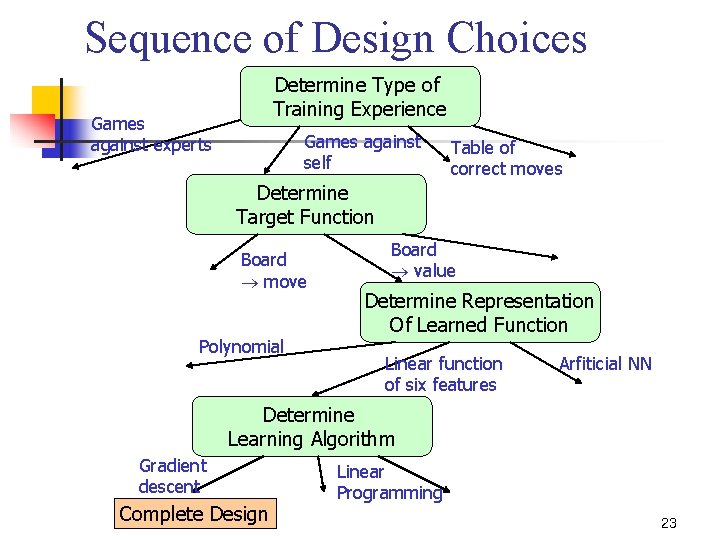
Designing a Learning System n n Choosing the Training Experience Choosing the Target Function Choosing a Representation for the Target Function Choosing a Function Approximation Algorithm 10

Choosing the Training Experience (1/2) n Key Attributes n Direct/indirect feedback n n n Direct feedback: checkers state and correct move Indirect feedback: move sequence and final outcomes Degree of controlling the sequence of training example n Learner가 학습 정보를 얻을 때 teacher의 도움을 받는 정도 11

Choosing the Training Experience (2/2) n Distribution of examples n 시스템의 성능을 평가하는 테스트의 예제 분포 를 잘 반영해야 함 12

Choosing the Target Function (1/2) n A function that chooses the best move M for any B n n n Choose. Move : B M Difficult to learn It is useful to reduce the problem of improving performance P at task T to the problem of learning some particular target function. 13

Choosing the Target Function (2/2) n An evaluation function that assigns a numerical score to any B n V : B R 14

Target Function for the Checkers Problem n Algorithm n n If b is a final state that is won, then V(b) = 100 ……. that is lost, then V(b)=-100 ……. that is drawn, then V(b)=0 If b is not a final state, then V(b)=V(b’), where b’ is the best final board state 15

Choosing a Representation for the Target Function n Describing the function n n Tables Rules Polynomial functions Neural nets Trade-off in choice n n Expressive power Size of training data 16

Linear Combination as Representation (b) = w 0 + w 1 x 1 + w 2 x 2 + w 3 x 3 +w 4 x 4 + w 5 x 5 + w 6 x 6 x 1: # of black pieces on the board x 2: # of red pieces on the board x 3: # of black kings on the board x 4: # of red kings on the board x 5: # of black pieces threatened by red x 6: # of red pieces threatened by black w 1 - w 6: weights 17

Partial Design of a Checkers Learning Program n Task T: playing checkers Performance measure P: Percent of games won in the world tournament Training experience E: games played against itself Target function V: Board R Target function representation n (b) = w 0 + w 1 x 1 + w 2 x 2 + w 3 x 3 + w 4 x 4 + w 5 x 5 + w 6 x 6 n n 18

Choosing a Function Approximation Algorithm n A training example is represented as an ordered pair <b, Vtrain(b)> n n n b: board state Vtrain(b): training value for b Instance: “black has won the game (x 2 = 0) <<x 1=3, x 2=0, x 3=1, x 4=0, x 5=0, x 6=0>, +100> 19

Choosing a Function Approximation Algorithm n Estimating training values for intermediate board states n n n Vtrain(b) (Successor(b)) : current approximation to V Successor(b): the next board state 20

Adjusting the Weights (1/2) n n Choosing wi to best fit the training examples Minimize the squared error 21

Adjusting the Weights (2/2) n LMS Weight Update Rule For each training example <b, Vtrain(b)> 1. Use the current weights to calculate V’(b) 2. For each weight wi, update it as 22

Sequence of Design Choices Determine Type of Training Experience Games against experts Games against self Table of correct moves Determine Target Function Board move Polynomial Board value Determine Representation Of Learned Function Linear function of six features Arfiticial NN Determine Learning Algorithm Gradient descent Complete Design Linear Programming 23

Perspectives in ML n n “Learning as search in a space of possible hypotheses” Representations for hypotheses n n Linear functions Logical descriptions Decision trees Neural networks 24

Perspectives in ML n Learning methods are characterized by their search strategies and by the underlying structure of the search spaces. 25

Neural Networks

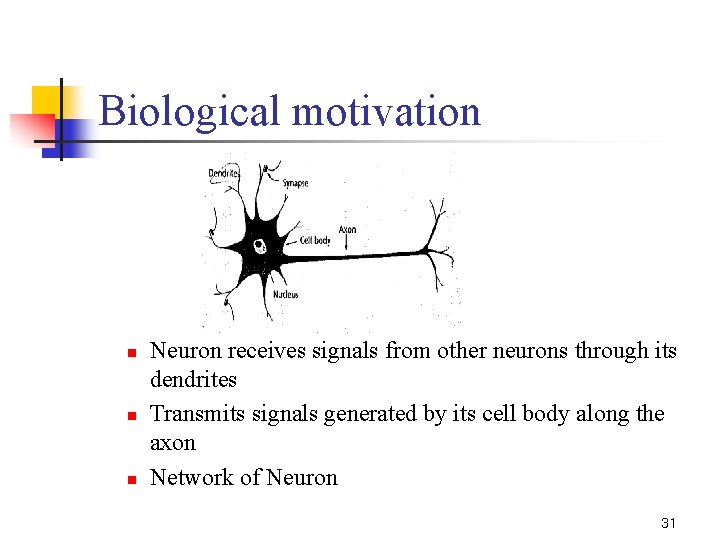
Biological motivation n Neuron receives signals from other neurons through its dendrites Transmits signals generated by its cell body along the axon Network of Neuron 31

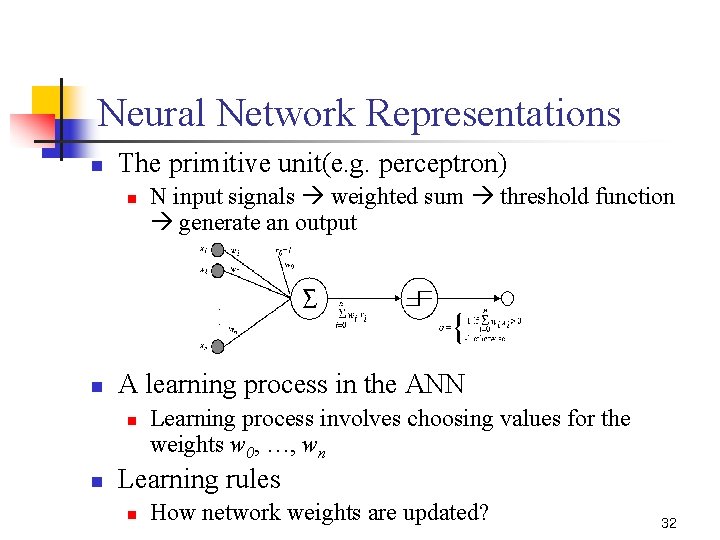
Neural Network Representations n The primitive unit(e. g. perceptron) n n A learning process in the ANN n n N input signals weighted sum threshold function generate an output Learning process involves choosing values for the weights w 0, …, wn Learning rules n How network weights are updated? 32

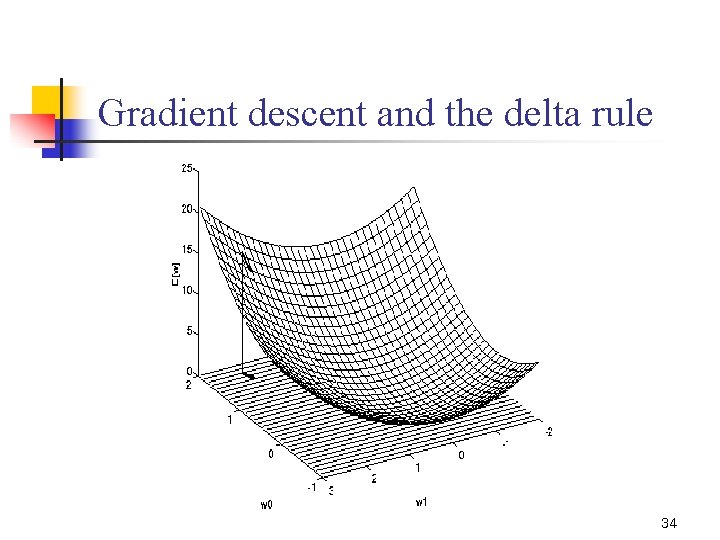
Gradient descent and the delta rule n The delta rule n Linear unit for which the output o is given by n Measure for the training error of a hypothesis n n d : the set of traing examples td : the target output for training example d od : the output of the linear unit for training example d We can characterize E as a function of 33

Gradient descent and the delta rule 34

Gradient descent and the delta rule n Derivation of the gradient descent rule n Direction of steepest descent along the error space n n Derivative E with respect to each component of The negative of this vector therefore gives the direction of steepest decrease 35

Gradient descent and the delta rule n Training rule for gradient descent n wi ← wi + wi where, n Efficient way of calculating the gradient n So, 36

Gradient descent and the delta rule n n If is too large, the gradient descent search runs the risk of overstepping the minimum gradually reduce the value of 37

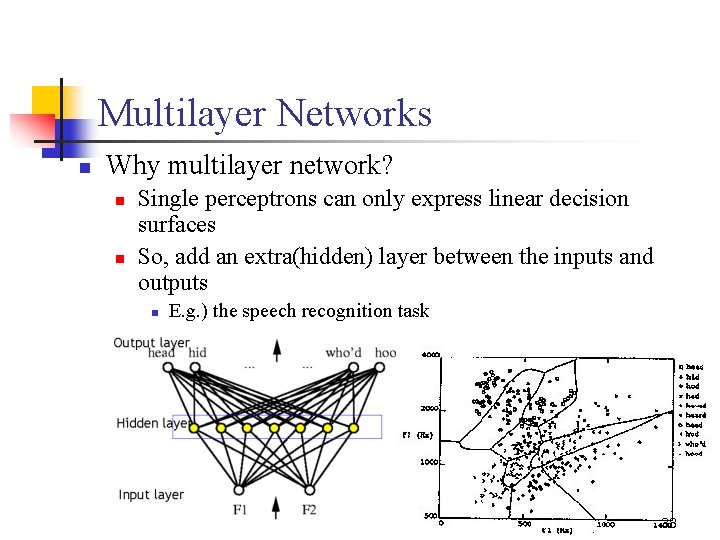
Multilayer Networks n Why multilayer network? n n Single perceptrons can only express linear decision surfaces So, add an extra(hidden) layer between the inputs and outputs n E. g. ) the speech recognition task 38

Multilayer Networks n Sigmoid function 39

Error Function for BP n E defined as a sum of the squared errors over all the output units k for all the training examples d. 40

BP Algorithm 41

Learning Until… n n n After a fixed number of iterations (epochs) Once the error falls below some threshold Once the validation error meets some criterion 42

Self Organizing Map

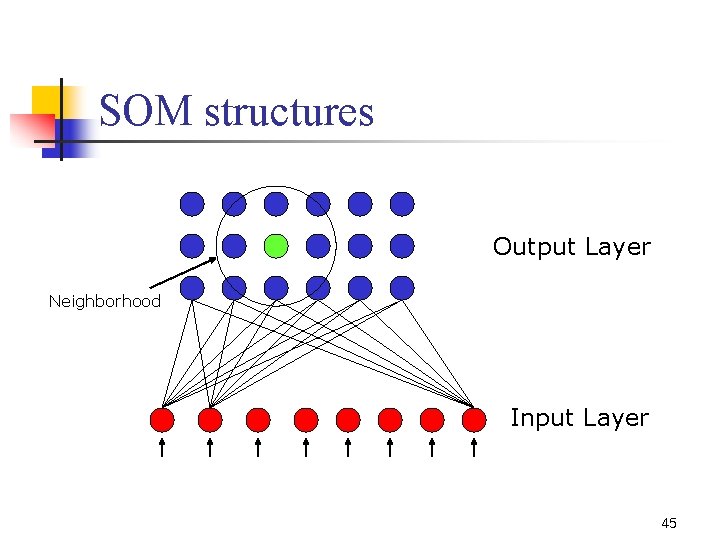
Introduction n n Unsupervised Learning SOM (Self Organizing Map) n n Visualization Abstraction 44

SOM structures Output Layer Neighborhood Input Layer 45

Data to be clustered 46

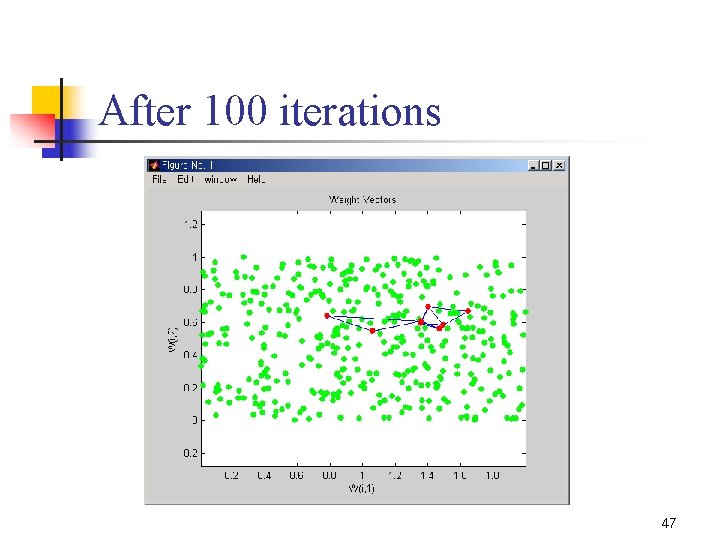
After 100 iterations 47

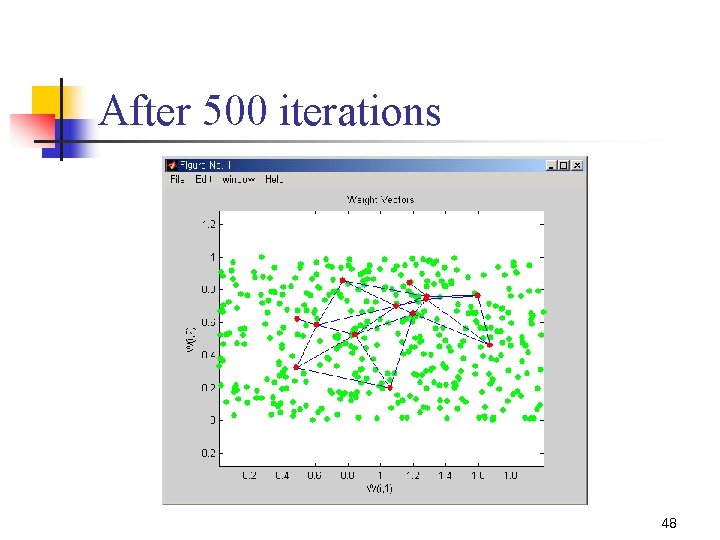
After 500 iterations 48

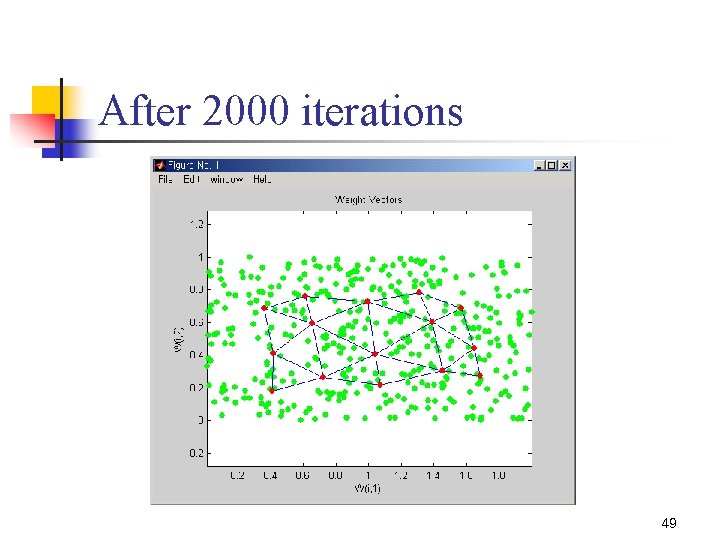
After 2000 iterations 49

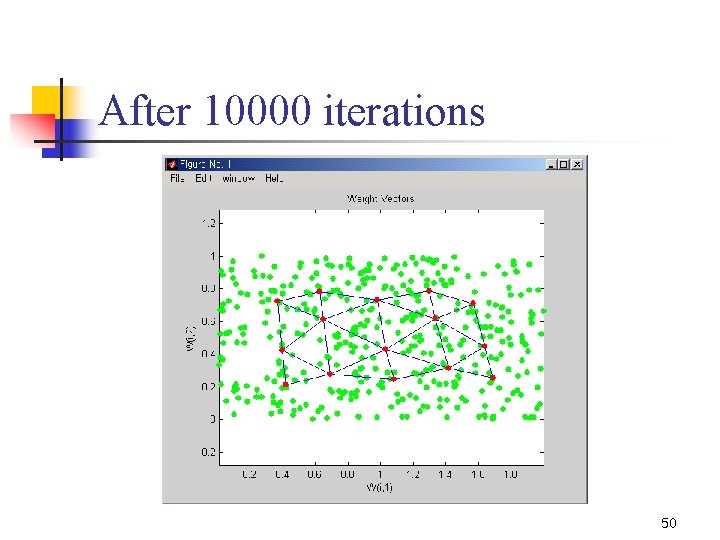
After 10000 iterations 50