Machine Learning Group SemiSupervised Clustering and its Application

Machine Learning Group Semi-Supervised Clustering and its Application to Text Clustering and Record Linkage Raymond J. Mooney Sugato Basu Mikhail Bilenko Arindam Banerjee University of Texas at Austin

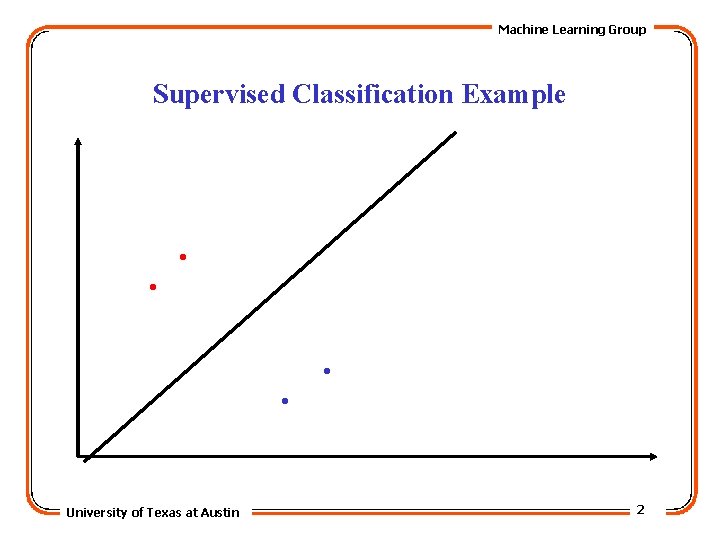
Machine Learning Group Supervised Classification Example . . University of Texas at Austin 2

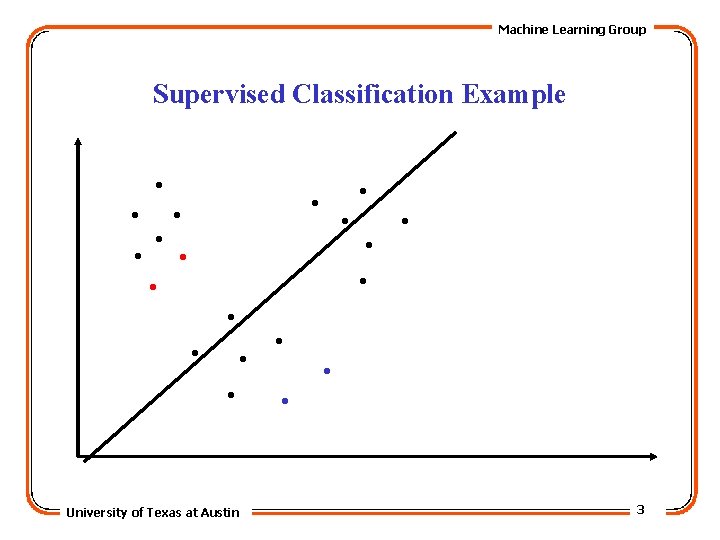
Machine Learning Group Supervised Classification Example . . University of Texas at Austin 3

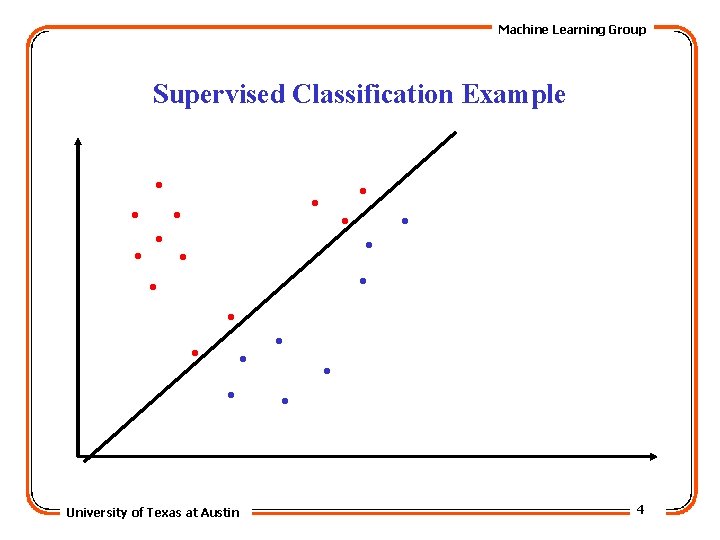
Machine Learning Group Supervised Classification Example . . University of Texas at Austin 4

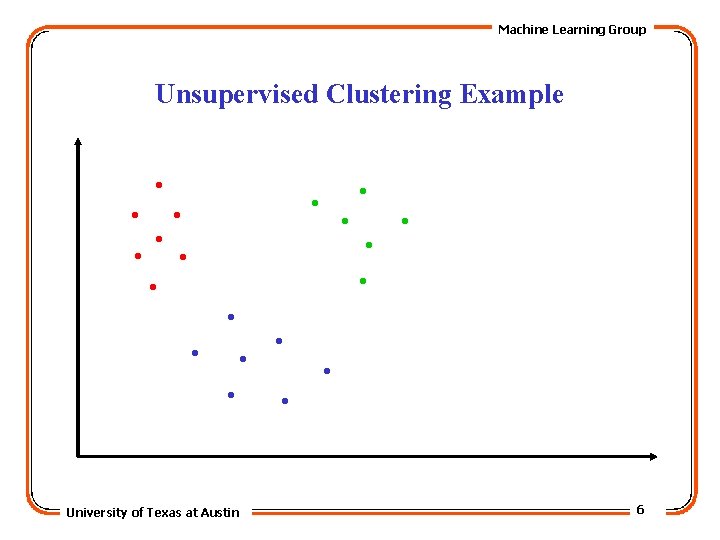
Machine Learning Group Unsupervised Clustering Example . . University of Texas at Austin 5

Machine Learning Group Unsupervised Clustering Example . . University of Texas at Austin 6

Machine Learning Group Semi-Supervised Learning • Combines labeled and unlabeled data during training to improve performance: – Semi-supervised classification: Training on labeled data exploits additional unlabeled data, frequently resulting in a more accurate classifier. – Semi-supervised clustering: Uses small amount of labeled data to aid and bias the clustering of unlabeled data. University of Texas at Austin 7

Machine Learning Group Semi-Supervised Classification Example . . University of Texas at Austin 8

Machine Learning Group Semi-Supervised Classification Example . . University of Texas at Austin 9

Machine Learning Group Semi-Supervised Classification • Algorithms: – Semisupervised EM [Ghahramani: NIPS 94, Nigam: ML 00]. – Co-training [Blum: COLT 98]. – Transductive SVM’s [Vapnik: 98, Joachims: ICML 99]. • Assumptions: – Known, fixed set of categories given in the labeled data. – Goal is to improve classification of examples into these known categories. University of Texas at Austin 10

Machine Learning Group Semi-Supervised Clustering Example . . University of Texas at Austin 11

Machine Learning Group Semi-Supervised Clustering Example . . University of Texas at Austin 12

Machine Learning Group Second Semi-Supervised Clustering Example . . University of Texas at Austin 13

Machine Learning Group Second Semi-Supervised Clustering Example . . University of Texas at Austin 14

Machine Learning Group Semi-Supervised Clustering • Can group data using the categories in the initial labeled data. • Can also extend and modify the existing set of categories as needed to reflect other regularities in the data. • Can cluster a disjoint set of unlabeled data using the labeled data as a “guide” to the type of clusters desired. University of Texas at Austin 15

Machine Learning Group Search-Based Semi-Supervised Clustering • Alter the clustering algorithm that searches for a good partitioning by: – Modifying the objective function to give a reward for obeying labels on the supervised data [Demeriz: ANNIE 99]. – Enforcing constraints (must-link, cannot-link) on the labeled data during clustering [Wagstaff: ICML 00, Wagstaff: ICML 01]. – Use the labeled data to initialize clusters in an iterative refinement algorithm (k. Means, EM) [Basu: ICML 02]. University of Texas at Austin 16

Machine Learning Group Unsupervised KMeans Clustering • KMeans is a partitional clustering algorithm based on iterative relocation that partitions a dataset into K clusters. Algorithm: Initialize K cluster centers randomly. Repeat until convergence: – Cluster Assignment Step: Assign each data point x to the cluster Xl, such that L 2 distance of x from (center of Xl) is minimum – Center Re-estimation Step: Re-estimate each cluster center as the mean of the points in that cluster University of Texas at Austin 17

Machine Learning Group KMeans Objective Function • Locally minimizes sum of squared distance between the data points and their corresponding cluster centers: • Initialization of K cluster centers: – Totally random – Random perturbation from global mean – Heuristic to ensure well-separated centers etc. University of Texas at Austin 18

Machine Learning Group K Means Example University of Texas at Austin 19

Machine Learning Group K Means Example Randomly Initialize Means x x University of Texas at Austin 20

Machine Learning Group K Means Example Assign Points to Clusters x x University of Texas at Austin 21

Machine Learning Group K Means Example Re-estimate Means x x University of Texas at Austin 22

Machine Learning Group K Means Example Re-assign Points to Clusters x x University of Texas at Austin 23

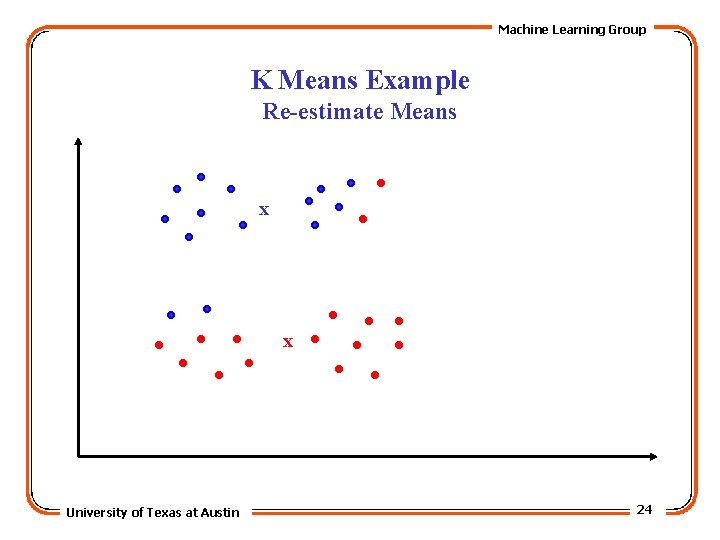
Machine Learning Group K Means Example Re-estimate Means x x University of Texas at Austin 24

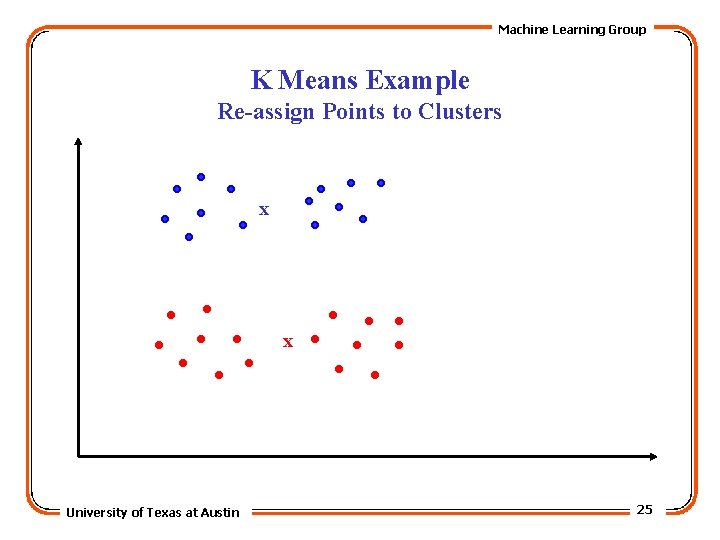
Machine Learning Group K Means Example Re-assign Points to Clusters x x University of Texas at Austin 25

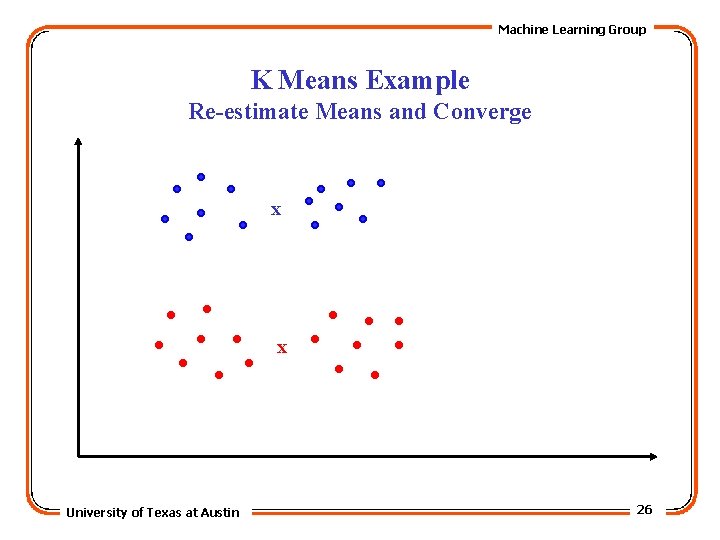
Machine Learning Group K Means Example Re-estimate Means and Converge x x University of Texas at Austin 26

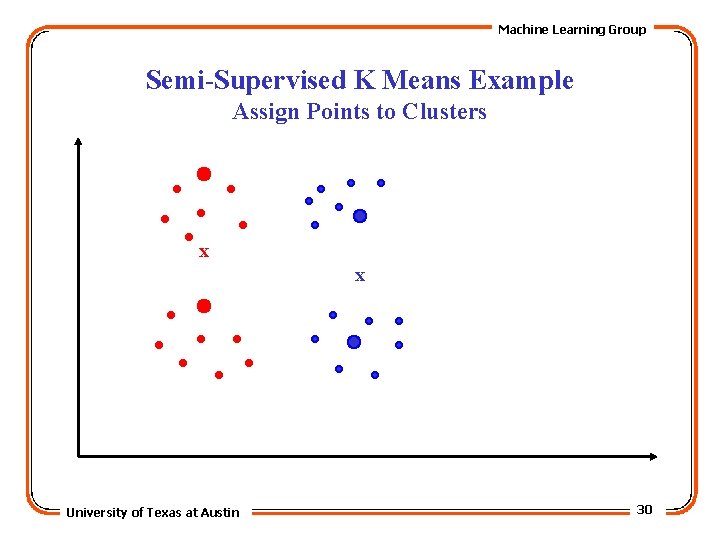
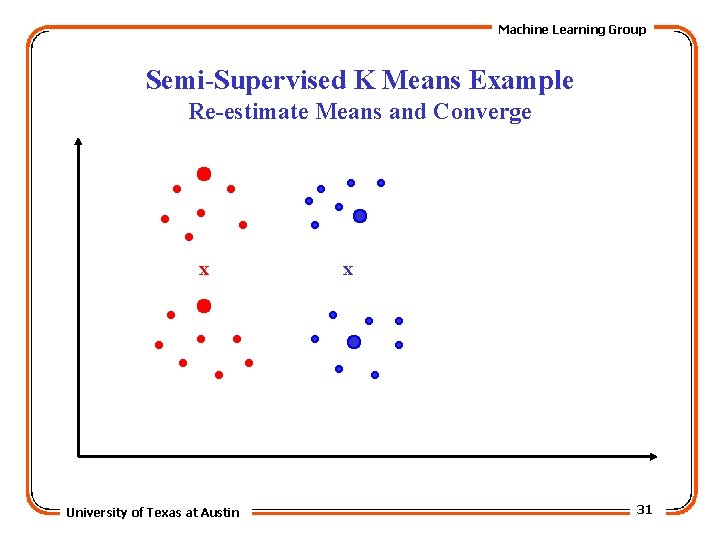
Machine Learning Group Semi-Supervised KMeans • Seeded KMeans: – Labeled data provided by user are used for initialization: initial center for cluster i is the mean of the seed points having label i. – Seed points are only used for initialization, and not in subsequent steps. • Constrained KMeans: – Labeled data provided by user are used to initialize KMeans algorithm. – Cluster labels of seed data are kept unchanged in the cluster assignment steps, and only the labels of the non-seed data are reestimated. University of Texas at Austin 27

Machine Learning Group Semi-Supervised K Means Example University of Texas at Austin 28

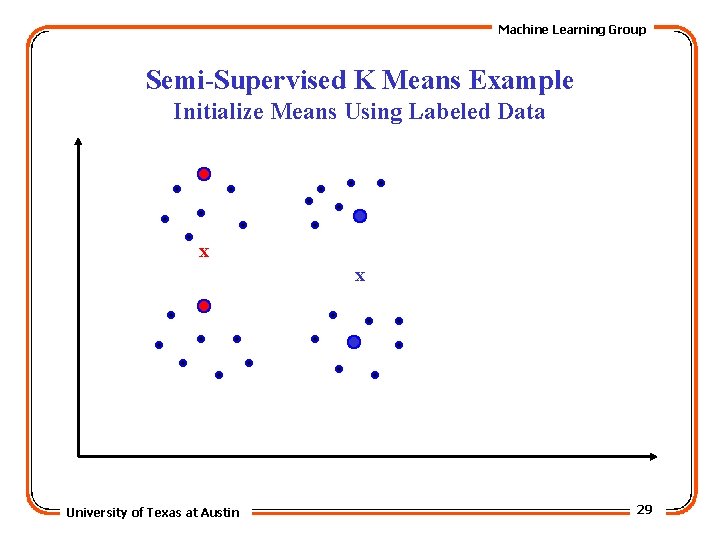
Machine Learning Group Semi-Supervised K Means Example Initialize Means Using Labeled Data x x University of Texas at Austin 29

Machine Learning Group Semi-Supervised K Means Example Assign Points to Clusters x x University of Texas at Austin 30

Machine Learning Group Semi-Supervised K Means Example Re-estimate Means and Converge x University of Texas at Austin x 31

Machine Learning Group Similarity-Based Semi-Supervised Clustering • Train an adaptive similarity function to fit the labeled data. • Use a standard clustering algorithm with the trained similarity function to cluster the unlabeled data. • Adaptive similarity functions: – Altered Euclidian distance [Klein: ICML 02] – Trained Mahalanobis distance [Xing: NIPS 02] – EM-trained edit distance [Bilenko: KDD 03] • Clustering algorithms: – Single-link agglomerative [Bilenko: KDD 03] – Complete-link agglomerative [Klein: ICML 02] – K-means [Xing: NIPS 02] University of Texas at Austin 32

Machine Learning Group Semi-Supervised Clustering Example Similarity Based University of Texas at Austin 33

Machine Learning Group Semi-Supervised Clustering Example Distances Transformed by Learned Metric University of Texas at Austin 34

Machine Learning Group Semi-Supervised Clustering Example Clustering Result with Trained Metric University of Texas at Austin 35

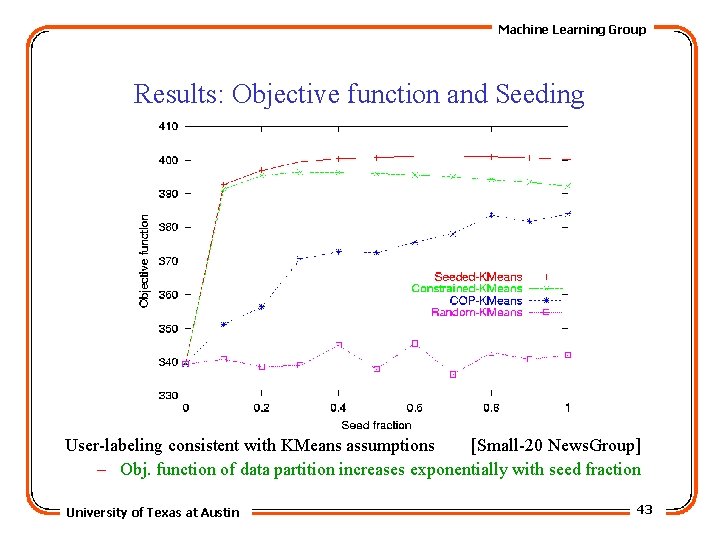
Machine Learning Group Experiments • Evaluation measures: – Objective function value for KMeans. – Mutual Information (MI) between distributions of computed cluster labels and human-provided class labels. • Experiments: – Change of fraction of – Change of noise in seeding). objective function and MI with increasing seeding (for complete labeling and no noise). objective function and MI with increasing seeds (for complete labeling and fixed University of Texas at Austin 36

Machine Learning Group Experimental Methodology • Clustering algorithm is always run on the entire dataset. • Learning curves with 10 -fold cross-validation: – 10% data set aside as test set whose label is always hidden. – Learning curve generated by training on different “seed fractions” of the remaining 90% of the data whose label is provided. • Objective function is calculated over the entire dataset. • MI measure calculated only on the independent test set. University of Texas at Austin 37

Machine Learning Group Experimental Methodology (contd. ) • For each fold in the Seeding experiments: – Seeds selected from training dataset by varying seed fraction from 0. 0 to 1. 0, in steps of 0. 1 • For each fold in the Noise experiments: – Noise simulated by changing the labels of a fraction of the seed values to a random incorrect value. University of Texas at Austin 38

Machine Learning Group COP-KMeans • COPKMeans [Wagstaff et al. : ICML 01] is KMeans with must-link (must be in same cluster) and cannot-link (cannot be in same cluster) constraints on data points. • Initialization: Cluster centers are chosen randomly, but as each one is chosen any must-link constraints that it participates in are enforced (so that they cannot later be chosen as the center of another cluster). • Algorithm: During cluster assignment step in COPKMeans, a point is assigned to its nearest cluster without violating any of its constraints. If no such assignment exists, abort. University of Texas at Austin 39

Machine Learning Group Datasets • Data sets: – UCI Iris (3 classes; 150 instances) – CMU 20 Newsgroups (20 classes; 20, 000 instances) – Yahoo! News (20 classes; 2, 340 instances) • Data subsets created for experiments: – Small-20 newsgroup: random sample of 100 documents from each newsgroup, created to study effect of datasize on algorithms. – Different-3 newsgroup: 3 very different newsgroups (alt. atheism, rec. sport. baseball, sci. space), created to study effect of data separability on algorithms. – Same-3 newsgroup: 3 very similar newsgroups (comp. graphics, comp. os. ms-windows, comp. windows. x). University of Texas at Austin 40

Machine Learning Group Text Data • Vector space model with TF-IDF weighting for text data. • Non-content bearing words removed: – Stopwords – High and low frequency words – Words of length < 3 • Text-handling software: – Spherical KMeans was used as the underlying clustering algorithm: it uses cosine-similarity instead of Euclidean distance between word vectors. – Code base built on top of MC and SPKMeans packages developed at UT Austin. University of Texas at Austin 41

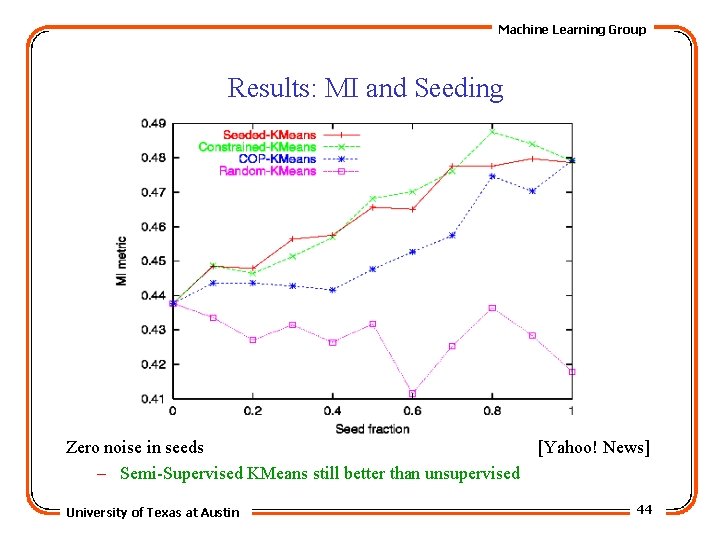
Machine Learning Group Results: MI and Seeding Zero noise in seeds [Small-20 News. Group] – Semi-Supervised KMeans substantially better than unsupervised KMeans University of Texas at Austin 42

Machine Learning Group Results: Objective function and Seeding User-labeling consistent with KMeans assumptions [Small-20 News. Group] – Obj. function of data partition increases exponentially with seed fraction University of Texas at Austin 43

Machine Learning Group Results: MI and Seeding Zero noise in seeds – Semi-Supervised KMeans still better than unsupervised University of Texas at Austin [Yahoo! News] 44

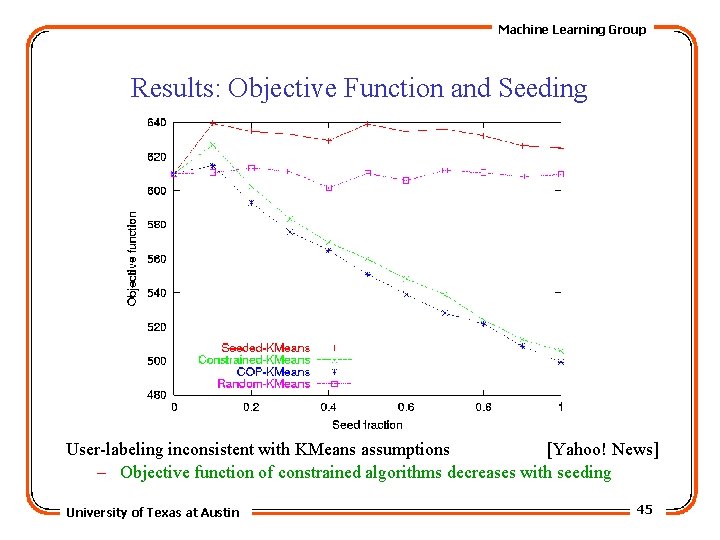
Machine Learning Group Results: Objective Function and Seeding User-labeling inconsistent with KMeans assumptions [Yahoo! News] – Objective function of constrained algorithms decreases with seeding University of Texas at Austin 45

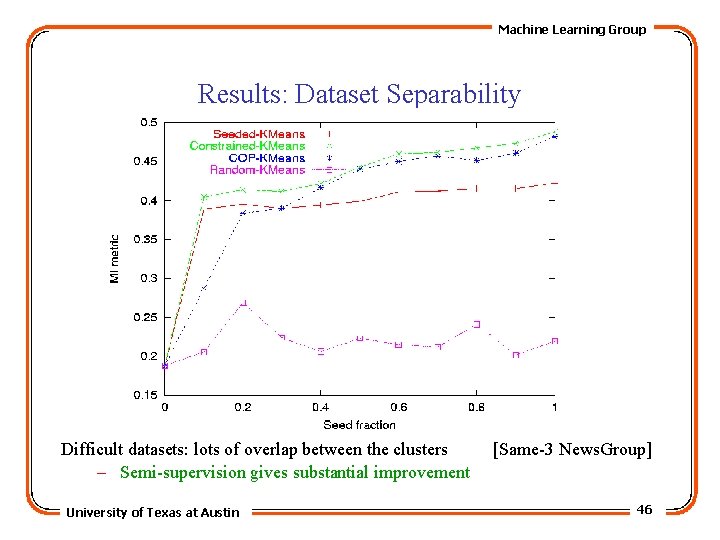
Machine Learning Group Results: Dataset Separability Difficult datasets: lots of overlap between the clusters – Semi-supervision gives substantial improvement University of Texas at Austin [Same-3 News. Group] 46

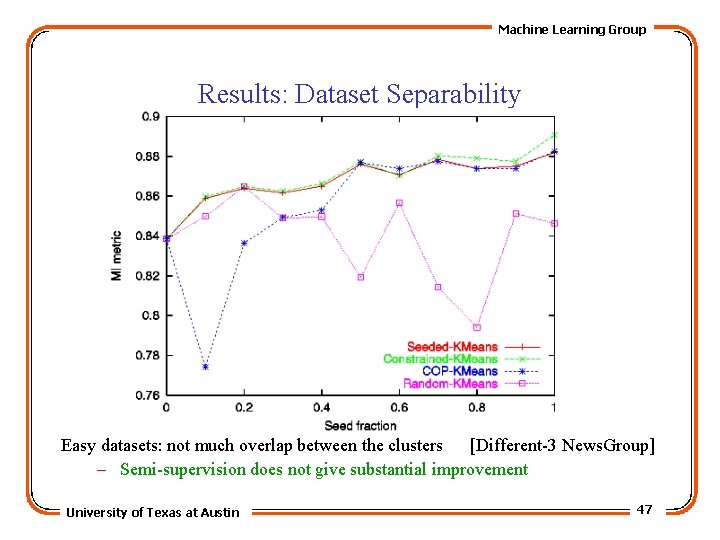
Machine Learning Group Results: Dataset Separability Easy datasets: not much overlap between the clusters [Different-3 News. Group] – Semi-supervision does not give substantial improvement University of Texas at Austin 47

Machine Learning Group Results: Noise Resistance Seed fraction: 0. 1 [20 News. Group] – Seeded-KMeans most robust against noisy seeding University of Texas at Austin 48

Machine Learning Group Record Linkage • Identify and merge duplicate field values and duplicate records in a database. • Applications – Duplicates in mailing lists – Information integration of multiple databases of stores, restaurants, etc. – Matching bibliographic references in research papers (Cora/Research. Index) – Different published editions in a database of books. University of Texas at Austin 49

Machine Learning Group Experimental Datasets • 1, 200 artificially corrupted mailing list addresses. • 1, 295 Cora research paper citations. • 864 restaurant listings from Fodor’s and Zagat’s guidebooks. • 1, 675 Citeseer research paper citations. University of Texas at Austin 50

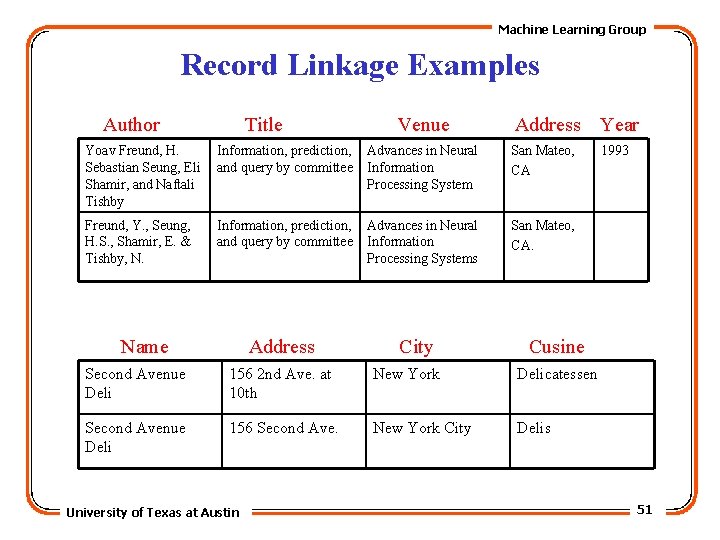
Machine Learning Group Record Linkage Examples Author Title Venue Address Year 1993 Yoav Freund, H. Sebastian Seung, Eli Shamir, and Naftali Tishby Information, prediction, and query by committee Advances in Neural Information Processing System San Mateo, CA Freund, Y. , Seung, H. S. , Shamir, E. & Tishby, N. Information, prediction, and query by committee Advances in Neural Information Processing Systems San Mateo, CA. Name Address City Cusine Second Avenue Deli 156 2 nd Ave. at 10 th New York Delicatessen Second Avenue Deli 156 Second Ave. New York City Delis University of Texas at Austin 51

Machine Learning Group Traditional Record Linkage • Apply a static text-similarity metric to each field. – Cosine similarity – Jaccard similarity – Edit distance • Combine similarity of each field to determine overall similarity. – Manually weighted sum • Threshold overall similarity to detect duplicates. University of Texas at Austin 52

Machine Learning Group Edit (Levenstein) Distance • Minimum number of character deletions, additions, or substitutions needed to make two strings equivalent. – “misspell” to “mispell” is distance 1 – “misspell” to “mistell” is distance 2 – “misspell” to “misspelling” is distance 3 • Can be computed efficiently using dynamic programming in O(mn) time where m and n are the lengths of the two strings being compared. University of Texas at Austin 53

Machine Learning Group Edit Distance with Affine Gaps • Contiguous deletions/additions are less expensive than non-contiguous ones. – “misspell” to “misspelling” is distance < 3 • Relative cost of contiguous and non-contiguous deletions/additions determined by a manually-set parameter. • Affine gap edit-distance better for identifying duplicates than Levenstein. University of Texas at Austin 54

Machine Learning Group Trainable Record Linkage • MARLIN (Multiply Adaptive Record Linkage using INduction) • Learn parameterized similarity metrics for comparing each field. – Trainable edit-distance • Use EM to set edit-operation costs • Learn to combine multiple similarity metrics for each field to determine equivalence. – Use SVM to decide on duplicates University of Texas at Austin 55

Machine Learning Group Trainable Edit Distance • Learnable edit distance based on generative probabilistic model for producing matched pairs of strings. • Parameters trained using EM to maximize the probability of producing training pairs of equivalent strings. • Originally developed for Levenstein distance by Ristad & Yianilos (1998). • We modified for affine gap edit distance. University of Texas at Austin 56

Machine Learning Group Sample Learned Edit Operations • Inexpensive operations: – Deleting/adding space – Substituting ‘/’ for ‘-’ in phone numbers – Deleting/adding ‘e’ and ‘t’ in addresses (Street St. ) • Expensive operations: – Deleting/adding a digit in a phone number. – Deleting/adding a ‘q’ in a name University of Texas at Austin 57

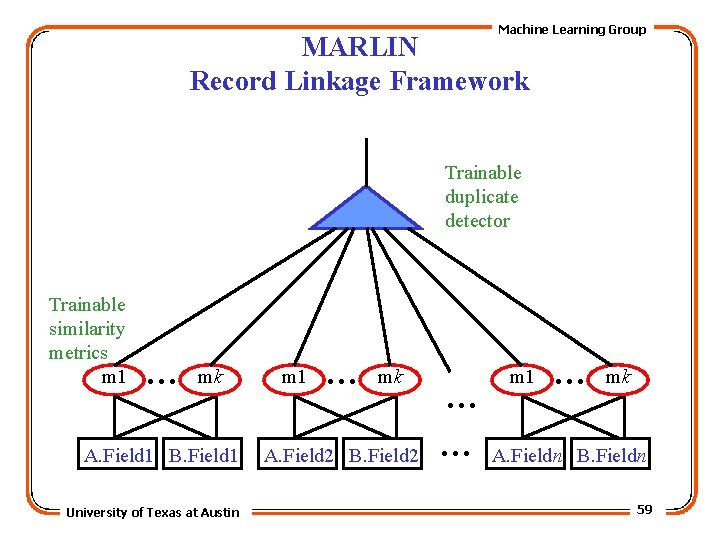
Machine Learning Group Combining Field Similarities • Record similarity is determined by combining the similarities of individual fields. • Some fields are more indicative of record similarity than others: – For addresses, city similarity is less relevant than restaurant/person name or street address. – For bibliographic citation, venue (i. e. conference or journal name) is less relevant than author or title. • Field similarities should be weighted when combined to determine record similarity. • Weights should be learned using learning algorithm. University of Texas at Austin 58

Machine Learning Group MARLIN Record Linkage Framework Trainable duplicate detector Trainable similarity metrics m 1 … mk A. Field 1 B. Field 1 University of Texas at Austin m 1 … mk A. Field 2 B. Field 2 … … m 1 … mk A. Fieldn B. Fieldn 59

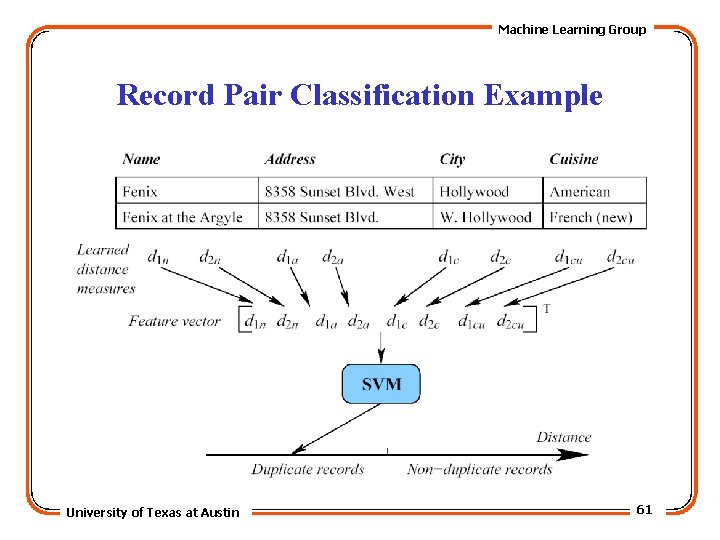
Machine Learning Group Learned Record Similarity • Field similarities used as feature vectors describing a pair of records. • SVM trained on these feature vectors to discriminate duplicate from non-duplicate pairs. • Record similarity based on distance of feature vector from the separator. University of Texas at Austin 60

Machine Learning Group Record Pair Classification Example University of Texas at Austin 61

Machine Learning Group Clustering Records into Equivalence Classes • Use similarity-based semi-supervised clustering to identify groups of equivalent records. • Use single-link agglomerative clustering to cluster records based on learned similarity metric. University of Texas at Austin 62

Machine Learning Group Experimental Methodology • 2 -fold cross-validation with equivalence classes of records randomly assigned to folds. • Results averaged over 20 runs of cross-validation. • Accuracy of duplicate detection on test data measured using: – Precision: – Recall: – F-Measure: University of Texas at Austin 63

Machine Learning Group Mailing List Name Field Results University of Texas at Austin 64

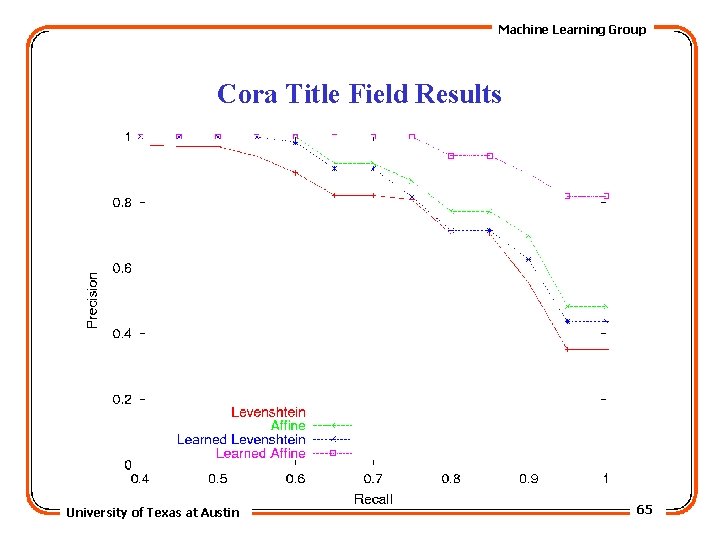
Machine Learning Group Cora Title Field Results University of Texas at Austin 65

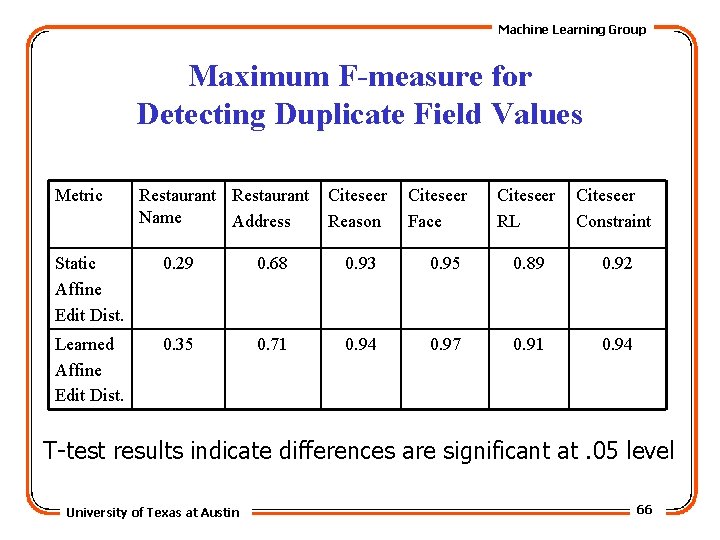
Machine Learning Group Maximum F-measure for Detecting Duplicate Field Values Metric Restaurant Name Address Citeseer Reason Citeseer Face Citeseer RL Citeseer Constraint Static Affine Edit Dist. 0. 29 0. 68 0. 93 0. 95 0. 89 0. 92 Learned Affine Edit Dist. 0. 35 0. 71 0. 94 0. 97 0. 91 0. 94 T-test results indicate differences are significant at. 05 level University of Texas at Austin 66

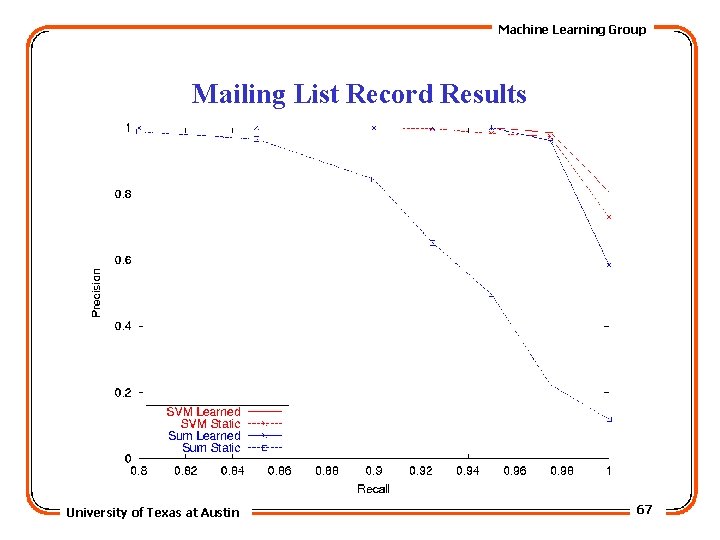
Machine Learning Group Mailing List Record Results University of Texas at Austin 67

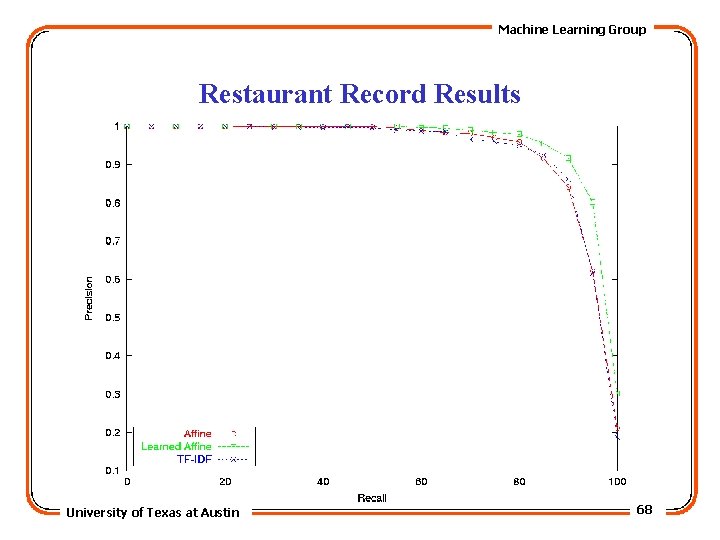
Machine Learning Group Restaurant Record Results University of Texas at Austin 68

Machine Learning Group Combining Similarity and Search-Based Semi-Supervised Clustering • Can apply seeded/constrained clustering with a trained similarity metric. • We developed a unified framework for Euclidian distance with soft pairwise-constraints (must-link, cannot-link). • Experiments on UCI data comparing approaches. • With small amounts of training, seeded/constrained tends to do better than similarity-based. • With larger amounts of labeled data, similarity-based tends to do better. • Combining both approaches outperforms both individual approaches. University of Texas at Austin 69

Machine Learning Group Active Semi-Supervision • Use active learning to select the most informative labeled examples. • We have developed an active approach for selecting good pairwise queries to get must-link and cannot-link constraints. – Should these two examples be in same or different clusters? • Experimental results on UCI and text data. • Active learning achieves much higher accuracy with fewer labeled training pairs. University of Texas at Austin 70

Machine Learning Group Future Work • Adaptive metric learning for vector-space cosine-similarity. – Supervised learning of better token weights than TF-IDF. • Unified method for text data (cosine similarity) that combines seeded/constrained with learned similarity measure. • Active learning results for duplicate detection. – Static-active learning • Exploiting external data/knowledge (e. g. from the web) for improving similarity measures for duplicate detection. University of Texas at Austin 71

Machine Learning Group Conclusion • Semi-supervised clustering is an alternative way of combining labeled and unlabeled data in learning. • Search-based and similarity-based are two alternative approaches. • They have useful applications in text-clustering and database record linkage. • Experimental results for these applications illustrate their utility. • They can be combined to produce even better results. University of Texas at Austin 72