Machine Learning Evolutionary Algorithm 2 Evolutionary Programming EP

Machine Learning Evolutionary Algorithm (2)

Evolutionary Programming

EP quick overview l l l Developed: USA in the 1960’s Early names: D. Fogel Typically applied to: – – l Attributed features: – – – l traditional EP: machine learning tasks by finite state machines contemporary EP: (numerical) optimization very open framework: any representation and mutation op’s OK crossbred with ES (contemporary EP) consequently: hard to say what “standard” EP is Special: – – no recombination self-adaptation of parameters standard (contemporary EP)

Evolutionary Programming (EP) l l There is no fixed structure for representation. There is only mutation operation, and cross-over is not used in this method. Each child is determined by its parent in a way of mutation. So, we can conclude that there are three steps: – – – Initialize population and calculate fitness values for initial population Mutate the parents and generate new population Calculate fitness values of new generation and continue from the second step. 4

EP technical summary tableau Representation Finite State Machine Recombination None Mutation Gaussian perturbation Parent selection Deterministic Survivor selection Probabilistic ( + ) Specialty Self-adaptation of mutation step sizes (in meta-EP)

Prediction by finite state machines l Finite state machine (FSM): – – – l States S Inputs I Outputs O Transition function : S x I S x O Transforms input stream into output stream Can be used for predictions, e. g. to predict next input symbol in a sequence

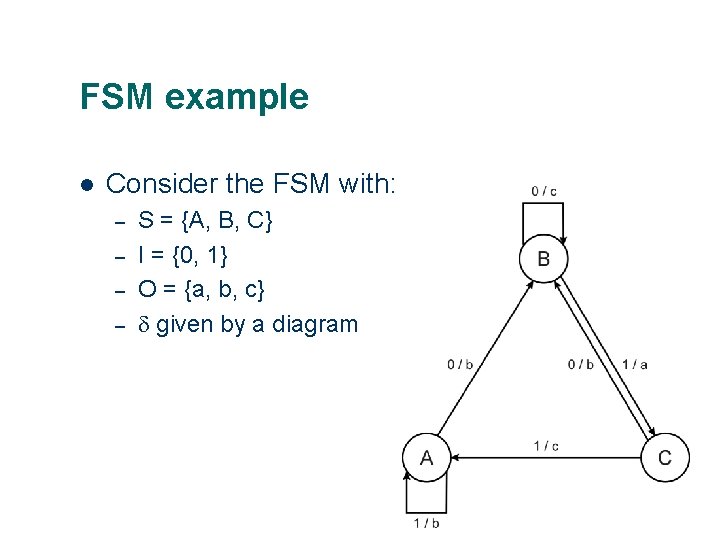
FSM example l Consider the FSM with: – – S = {A, B, C} I = {0, 1} O = {a, b, c} given by a diagram

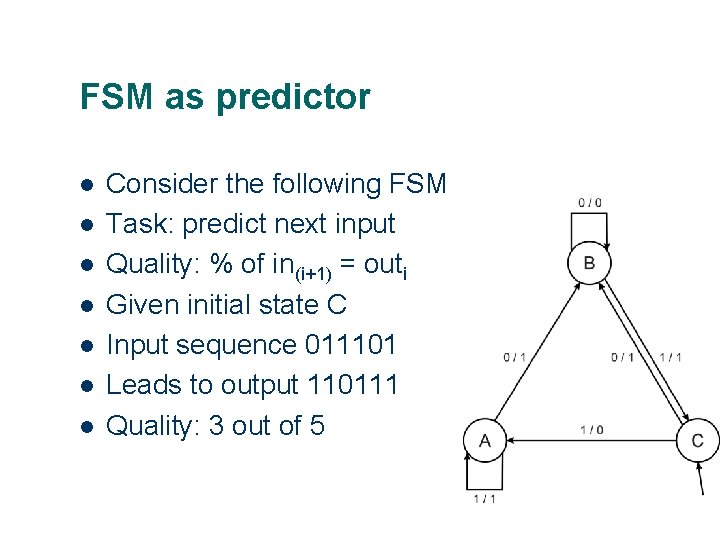
FSM as predictor l l l l Consider the following FSM Task: predict next input Quality: % of in(i+1) = outi Given initial state C Input sequence 011101 Leads to output 110111 Quality: 3 out of 5

Introductory example: evolving FSMs to predict primes l l l P(n) = 1 if n is prime, 0 otherwise I = N = {1, 2, 3, …, n, …} O = {0, 1} Correct prediction: outi= P(in(i+1)) Fitness function: – – – 1 point for correct prediction of next input 0 point for incorrect prediction Penalty for “too much” states

Introductory example: evolving FSMs to predict primes Parent selection: each FSM is mutated once l Mutation operators (one selected randomly): l – – – Change an output symbol Change a state transition (i. e. redirect edge) Add a state Delete a state Change the initial state

Genetic Programming

THE CHALLENGE "How can computers learn to solve problems without being explicitly programmed? In other words, how can computers be made to do what is needed to be done, without being told exactly how to do it? " Attributed to Arthur Samuel (1959)

GP quick overview Developed: USA in the 1990’s l Early names: J. Koza l Typically applied to: l – l Attributed features: – – – l machine learning tasks (prediction, classification…) competes with neural nets and alike needs huge populations (thousands) slow Special: – – non-linear chromosomes: trees, graphs mutation possible but not necessary (disputed!)

GP technical summary tableau Representation Tree structures Recombination Exchange of subtrees Mutation Random change in trees Parent selection Fitness proportional Survivor selection Generational replacement

REPRESENTATIONS l l l l Decision trees If-then production rules Horn clauses Neural nets Bayesian networks Frames Propositional logic l l l Binary decision diagrams Formal grammars Coefficients for polynomials Reinforcement learning tables Conceptual clusters Classifier systems

A COMPUTER PROGRAM

Introductory example: credit scoring l l Bank wants to distinguish good from bad loan applicants Model needed that matches historical data ID No of children Salary Marital status OK? ID-1 2 45000 Married 0 ID-2 0 30000 Single 1 ID-3 1 40000 Divorced 1 …

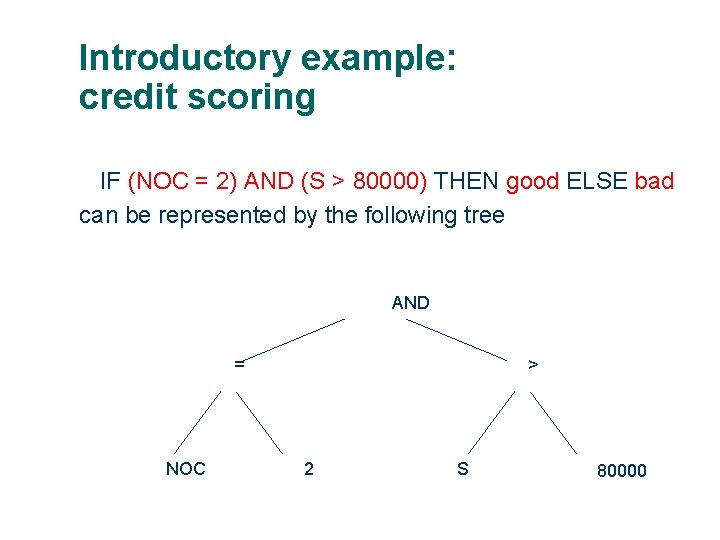
Introductory example: credit scoring A possible model: IF (NOC = 2) AND (S > 80000) THEN good ELSE bad l In general: IF formula THEN good ELSE bad l Only unknown is the right formula, hence l Natural fitness of a formula: percentage of well classified cases of the model it stands for l Natural representation of formulas (genotypes) is: parse trees l

Introductory example: credit scoring IF (NOC = 2) AND (S > 80000) THEN good ELSE bad can be represented by the following tree AND = NOC > 2 S 80000

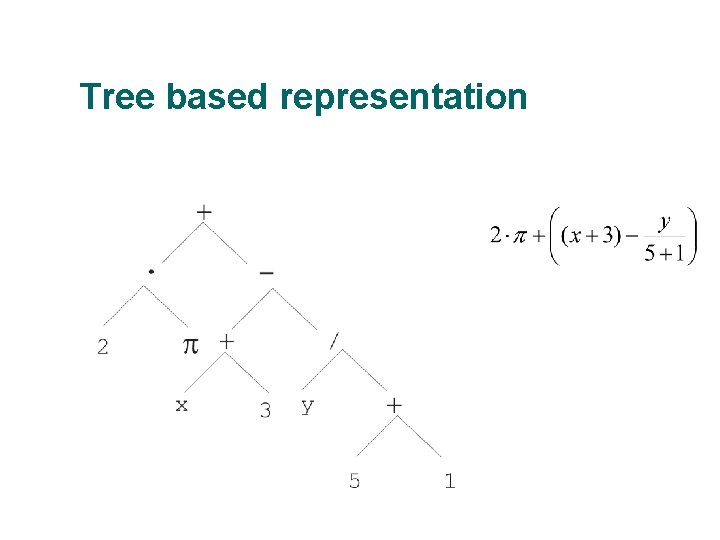
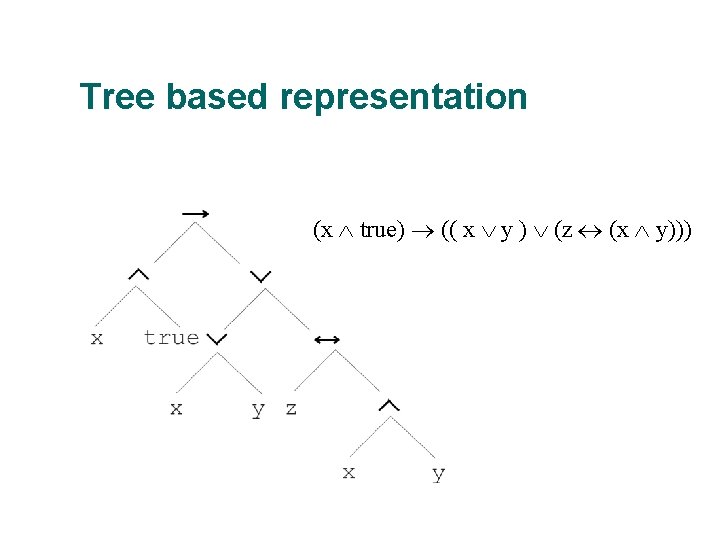
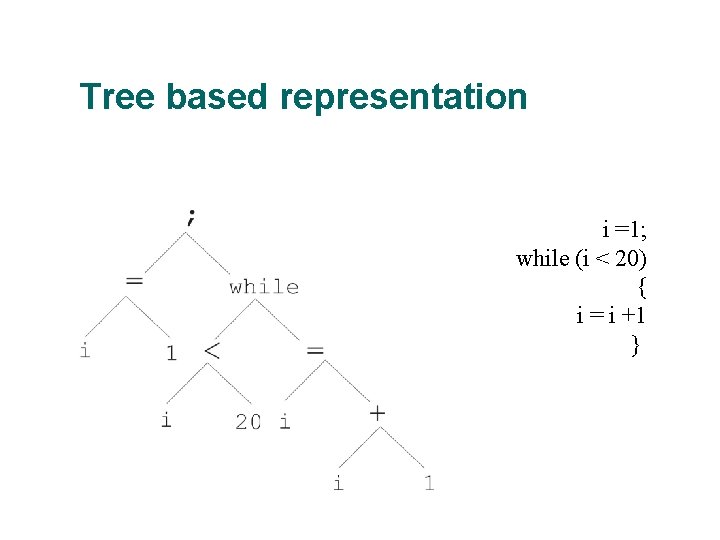
Tree based representation

Tree based representation (x true) (( x y ) (z (x y)))

Tree based representation i =1; while (i < 20) { i = i +1 }

Tree based representation l l In GA, ES, EP chromosomes are linear structures (bit strings, integer string, realvalued vectors, permutations) Tree shaped chromosomes are non-linear structures In GA, ES, EP the size of the chromosomes is fixed Trees in GP may vary in depth and width

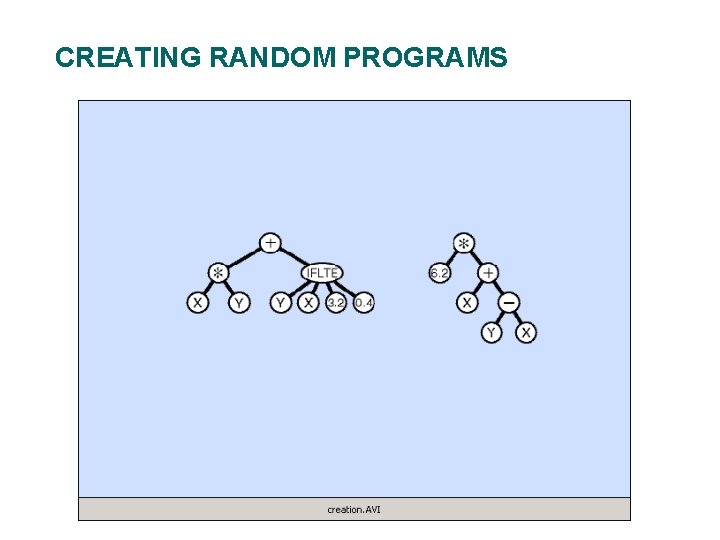
CREATING RANDOM PROGRAMS

Tree based representation l Symbolic expressions can be defined by – – l Adopting the following general recursive definition: 1. 2. 3. l Terminal set T Function set F (with the arities of function symbols) Every t T is a correct expression f(e 1, …, en) is a correct expression if f F, arity(f)=n and e 1, …, en are correct expressions There are no other forms of correct expressions In general, expressions in GP are not typed (closure property: any f F can take any g F as argument)

CREATING RANDOM PROGRAMS l Available functions F = {+, -, *, %, IFLTE} l Available terminals T = {X, Y, Random-Constants} l The random programs are: Of different sizes and shapes – Syntactically valid – Executable –

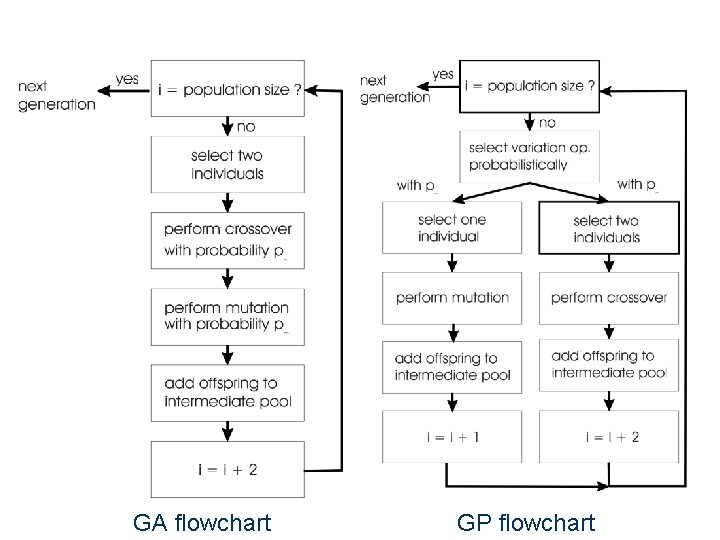
GA flowchart GP flowchart

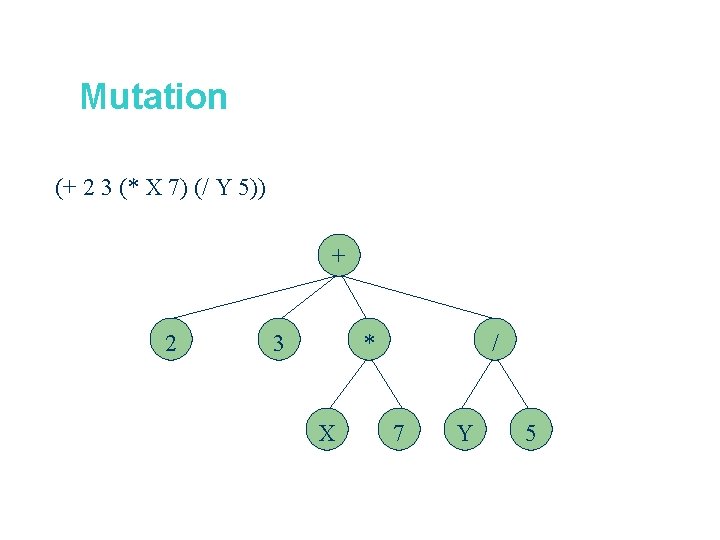
Mutation (+ 2 3 (* X 7) (/ Y 5)) + 2 3 * X / 7 Y 5

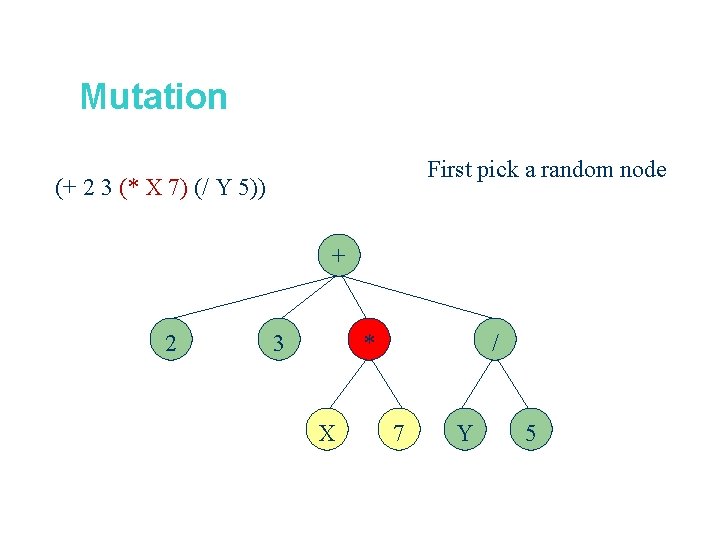
Mutation First pick a random node (+ 2 3 (* X 7) (/ Y 5)) + 2 * 3 X / 7 Y 5

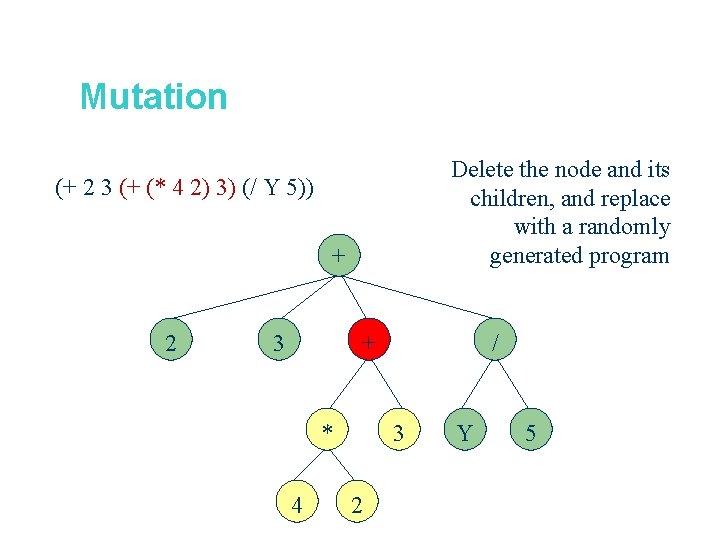
Mutation Delete the node and its children, and replace with a randomly generated program (+ 2 3 (+ (* 4 2) 3) (/ Y 5)) + 2 3 + * 4 / 3 2 Y 5

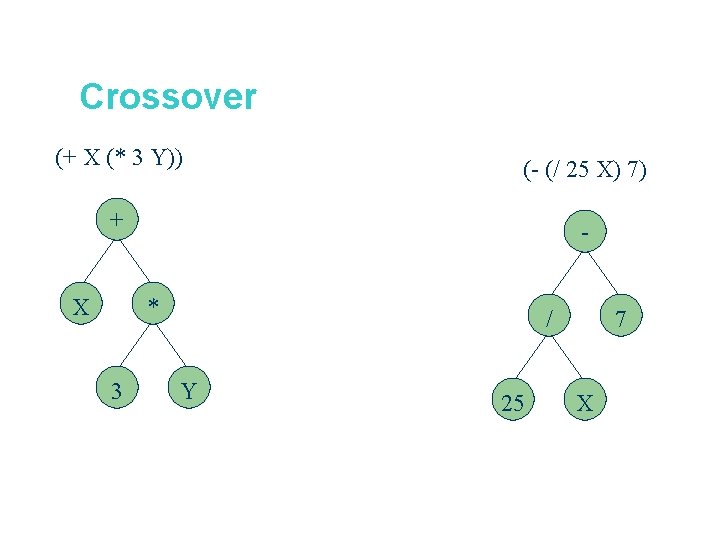
Crossover (+ X (* 3 Y)) (- (/ 25 X) 7) + - X * 3 / Y 25 7 X

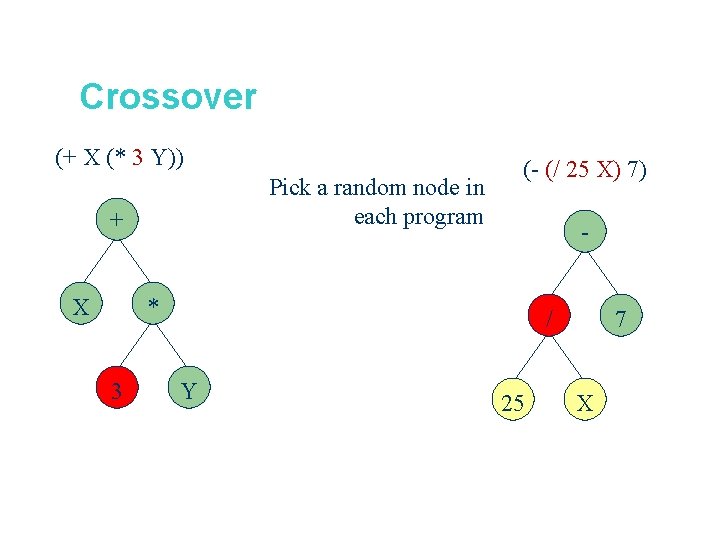
Crossover (+ X (* 3 Y)) Pick a random node in each program + X (- (/ 25 X) 7) - * 3 / Y 25 7 X

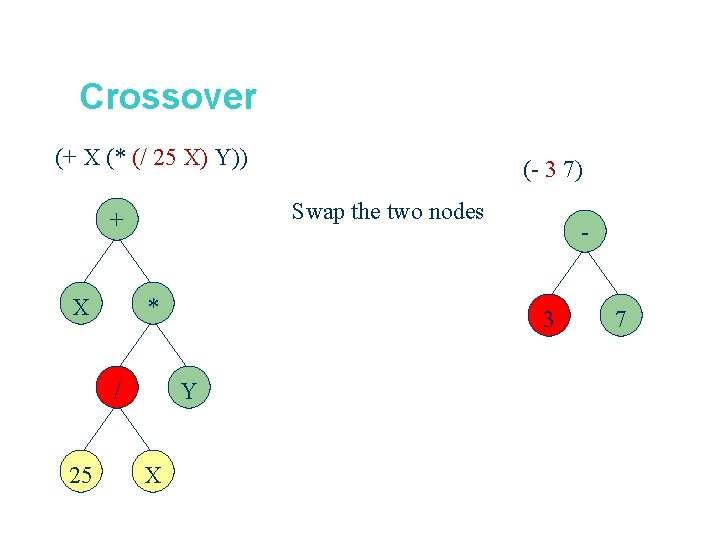
Crossover (+ X (* (/ 25 X) Y)) Swap the two nodes + X * / 25 (- 3 7) 3 Y X - 7

Mutation cont’d l Mutation has two parameters: – – l l Probability pm to choose mutation vs. recombination Probability to chose an internal point as the root of the subtree to be replaced Remarkably pm is advised to be 0 (Koza’ 92) or very small, like 0. 05 (Banzhaf et al. ’ 98) The size of the child can exceed the size of the parent

Recombination l l Most common recombination: exchange two randomly chosen subtrees among the parents Recombination has two parameters: – – l Probability pc to choose recombination vs. mutation Probability to chose an internal point within each parent as crossover point The size of offspring can exceed that of the parents

Selection l l Parent selection typically fitness proportionate Over-selection in very large populations – – – l rank population by fitness and divide it into two groups: group 1: best x% of population, group 2 other (100 -x)% 80% of selection operations chooses from group 1, 20% from group 2 for pop. size = 1000, 2000, 4000, 8000 x = 32%, 16%, 8%, 4% motivation: to increase efficiency, %’s come from rule of thumb Survivor selection: – – Typical: generational scheme (thus none) Recently steady-state is becoming popular for its elitism

Initialisation l l Maximum initial depth of trees Dmax is set Full method (each branch has depth = Dmax): – – l Grow method (each branch has depth Dmax): – – l nodes at depth d < Dmax randomly chosen from function set F nodes at depth d = Dmax randomly chosen from terminal set T nodes at depth d < Dmax randomly chosen from F T nodes at depth d = Dmax randomly chosen from T Common GP initialisation: ramped half-and-half, where grow & full method each deliver half of initial population

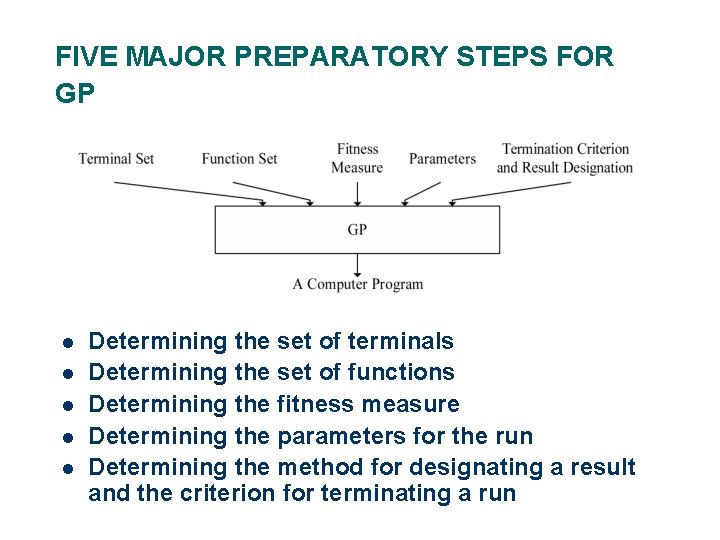
FIVE MAJOR PREPARATORY STEPS FOR GP l l l Determining the set of terminals Determining the set of functions Determining the fitness measure Determining the parameters for the run Determining the method for designating a result and the criterion for terminating a run

Building a Better Mouse l l Apply Genetic Programming to the problem of navigating a maze What are our terminal and function sets? – – Function Set = {If-Movement-Blocked, While-Not-At-Cheese*} Terminal Set = {Move-Forward, Turn-Left, Turn-Right} * While-Not-At-Cheese will be used exclusively as the root node of the parse tree

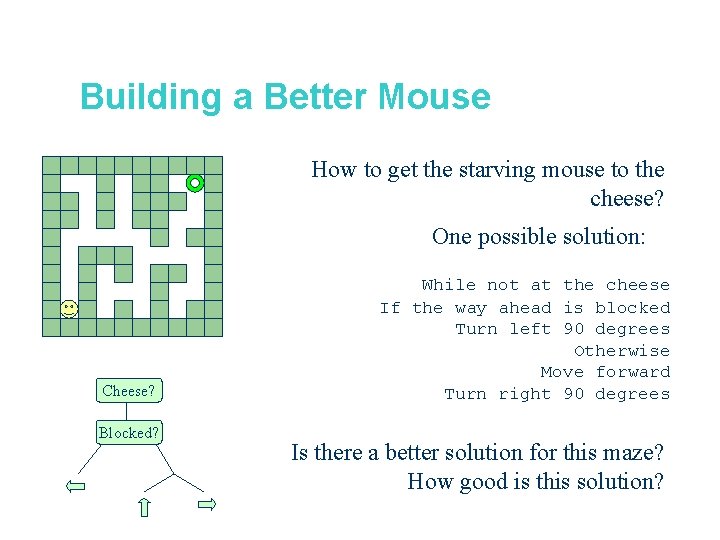
Building a Better Mouse How to get the starving mouse to the cheese? One possible solution: Cheese? Blocked? While not at the cheese If the way ahead is blocked Turn left 90 degrees Otherwise Move forward Turn right 90 degrees Is there a better solution for this maze? How good is this solution?

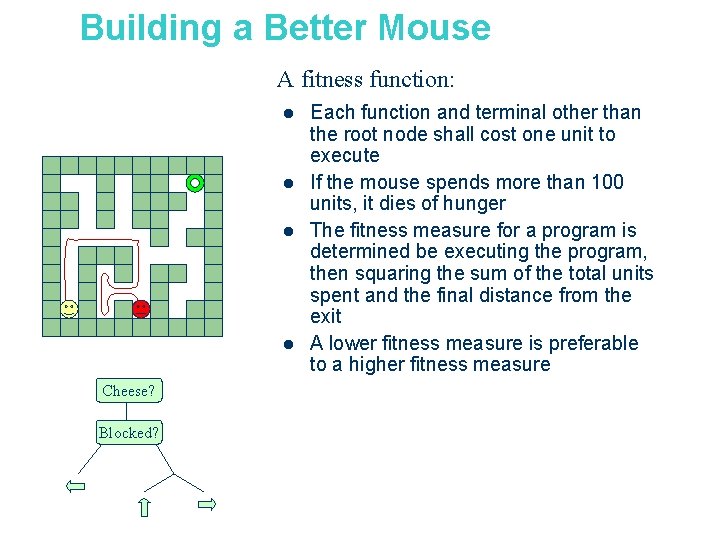
Building a Better Mouse A fitness function: l l Cheese? Blocked? Each function and terminal other than the root node shall cost one unit to execute If the mouse spends more than 100 units, it dies of hunger The fitness measure for a program is determined be executing the program, then squaring the sum of the total units spent and the final distance from the exit A lower fitness measure is preferable to a higher fitness measure

Building a Better Mouse While not at the cheese (12996) If the way ahead is blocked Turn left 90 degrees Otherwise Move forward one space While not at the cheese (12996) Move forward one space Turn right 90 degrees Turn left 90 degrees

Building a Better Mouse While not at the cheese (12996) If the way ahead is blocked Turn left 90 degrees Otherwise Move forward one space While not at the cheese (12996) Move forward one space Turn right 90 degrees Turn left 90 degrees Mutation: While not at the cheese (12996) If the way ahead is blocked Turn left 90 degrees Otherwise Turn left 90 degrees

Building a Better Mouse While not at the cheese (12996) If the way ahead is blocked Turn left 90 degrees Otherwise Move forward one space While not at the cheese (12996) Move forward one space Turn right 90 degrees Turn left 90 degrees Crossover: While not at the cheese (11664) If the way ahead is blocked Move forward one space Turn right 90 degrees Otherwise Move forward one space While not at the cheese (12996) Turn left 90 degrees

Building a Better Mouse (after 4202 generations, with 1000 programs per generation) Is this better? Fitness measure: 2809 While not at the cheese If the way ahead is blocked Turn right 90 degrees Move forward one space Otherwise Move forward one space Turn right 90 degrees Move forward one space Turn left 90 degrees If the way ahead is blocked Turn left 90 degrees Otherwise Move forward one space

Example We seek to find the Boolean function that returns particular Boolean output values (0 or 1). The Boolean even-k-parity function of k Boolean arguments returns T (true=1) if an even number of its Boolean arguments are T, and otherwise returns F (false =0) (fitness function). Let the input are D 0, D 1, and D 2. The output is S. Terminal set: D 0, D 1 and D 2 Function set: AND, OR, NAND, and NOR. Fitness cases: sum of 8 -combinations of the three Boolean arguments D 0, D 1, and D 2 (Truth Table) cases do not equals the correct value of the even-3 -parity function (error) construct 4 genes for this problem using Genetic Programming compute the fitness for these genes perform one crossover (best two genes) and one mutation operator for worst gene construct the new population

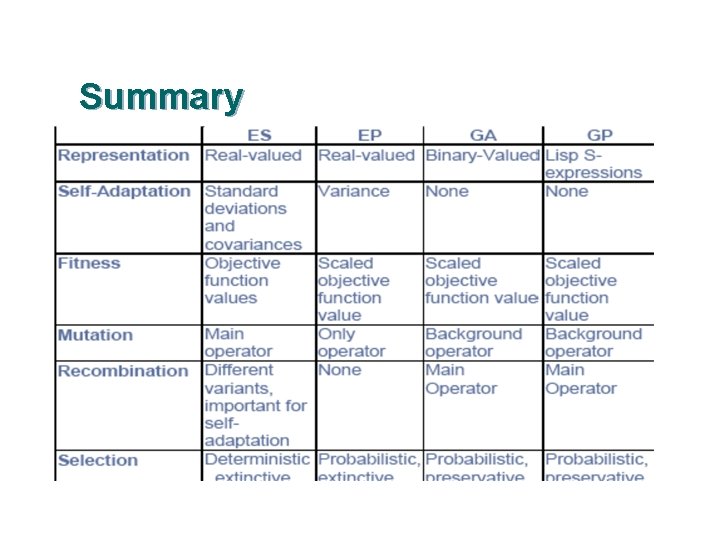
Summary 47