Machine Learning Chapter 10 Learning Sets of Rules

Machine Learning Chapter 10. Learning Sets of Rules Tom M. Mitchell

Learning Disjunctive Sets of Rules § Method 1: Learn decision tree, convert to rules § Method 2: Sequential covering algorithm: 1. Learn one rule with high accuracy, any coverage 2. Remove positive examples covered by this rule 3. Repeat 2

Sequential Covering Algorithm SEQUENTIALCOVERING (Target attribute; Attributes; Examples; Threshold) § Learned rules {} § Rule LEARN-ONERULE(Target_attribute, Attributes, Examples) § while PERFORMANCE (Rule, Examples) > Threshold, do – Learned_rules + Rule – Examples – {examples correctly classified by Rule} – Rule LEARN-ONERULE (Target_attribute, Attributes, Examples) – Learned_rules sort Learned_rules accord to PERFORMANCE over Examples – return Learned_rules 3

Learn-One-Rule 4

Learn-One-Rule(Cont. ) § § Pos positive Examples Neg negative Examples while Pos, do Learn a New. Rule - New. Rule most general rule possible - New. Rule Neg - while New. Rule. Neg, do Add a new literal to specialize New. Rule 1. Candidate literals generate candidates 2. Best_literal argmax. L Candidate literals Performance(Specialize. Rule(New. Rule; L)) 3. add Best_literal to New. Rule preconditions 4. New. Rule. Neg subset of New. Rule. Neg that satisfies New. Rule preconditions - Learned_rules + New. Rule - Pos – {members of Pos coverd by New. Rule} Return Learned_rules 5

Subtleties: Learn One Rule 1. May use beam search 2. Easily generalizes to multi-valued target functions 3. Choose evaluation function to guide search: – Entropy (i. e. , information gain) – Sample accuracy: where nc = correct rule predictions, n = all predictions § m estimate: 6

Variants of Rule Learning Programs § Sequential or simultaneous covering of data? § General specific, or specific general? § Generate-and-test, or example-driven? § Whether and how to post-prune? § What statistical evaluation function? 7

Learning First Order Rules Why do that? § Can learn sets of rules such as Ancestor(x, y) Parent(x; y) Ancestor(x; y) Parent(x; z) ^ Ancestor(z; y) § General purpose programming language PROLOG : programs are sets of such rules 8

First Order Rule for Classifying Web Pages [Slattery, 1997] course(A) has-word(A, instructor), Not has-word(A, good), link-from(A, B), has-word(B, assign), Not link-from(B, C) Train: 31/31, Test: 31/34 9

10

Specializing Rules in FOIL 11

Information Gain in FOIL 12

Induction as Inverted Deduction 13

Induction as Inverted Deduction(Cont’) 14

Induction as Inverted Deduction(Cont’) Induction is, in fact, the inverse operation of deduction, and cannot be conceived to exist without the corresponding operation, so that the question of relative importance cannot arise. Who thinks of asking whether addition or subtraction is the more important process in arithmetic? But at the same time much difference in difficulty may exist between a direct and inverse operation; : : : it must be allowed that inductive investigations are of a far higher degree of difficulty and complexity than any questions of deduction…. (Jevons 1874) 15

Induction as Inverted Deduction(Cont’) 16

Induction as Inverted Deduction(Cont’) 17

Induction as Inverted Deduction(Cont’) 18

Deduction: Resolution Rule 19

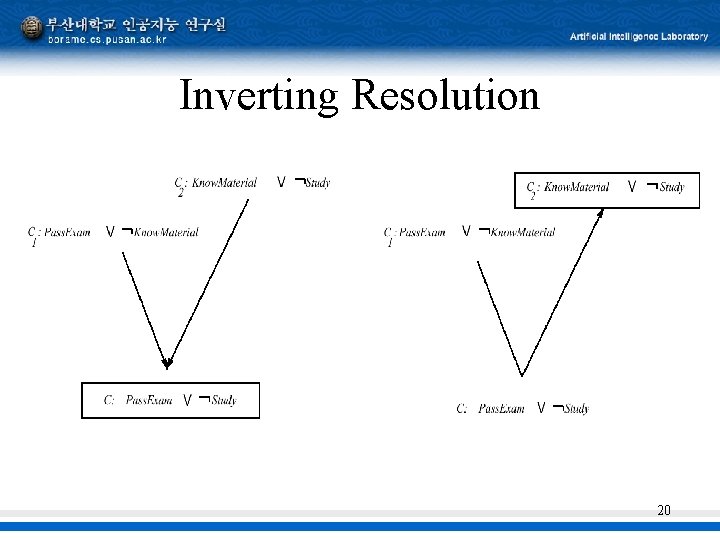
Inverting Resolution 20

Inverted Resolution (Propositional) 21

First order resolution 22

Inverting First order resolution 23

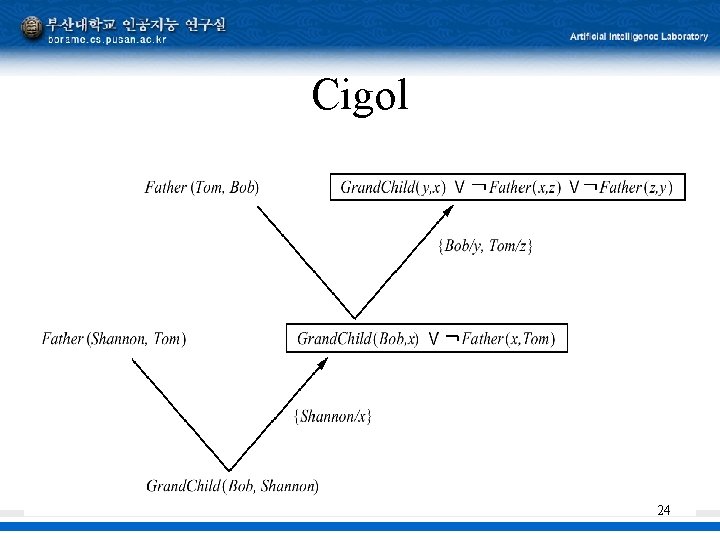
Cigol 24

Progol 25