Machine Learning Applications in Grid Computing George Cybenko

Machine Learning Applications in Grid Computing George Cybenko, Guofei Jiang and Daniel Bilar Thayer School of Engineering Dartmouth College 22 th Sept. , 1999, 37 th Allerton Conference Urbana-Champaign, Illinois Acknowledgements: This work was partially supported by AFOSR grants F 49620 -97 -1 -0382, NSF grant CCR-9813744 and DARPA contract F 30602 -98 -2 -0107.

Grid vision n Grid computing refers to computing in a distributed networked environment in which computing and data resources are located throughout the network. n Grid infrastructures provide basic infrastructure for computations that integrate geographically disparate resources, create a universal source of computing power that supports dramatically new classes of applications. n Several efforts are underway to build computational grids such as Globus, Infospheres and DARPA Co. ABS.

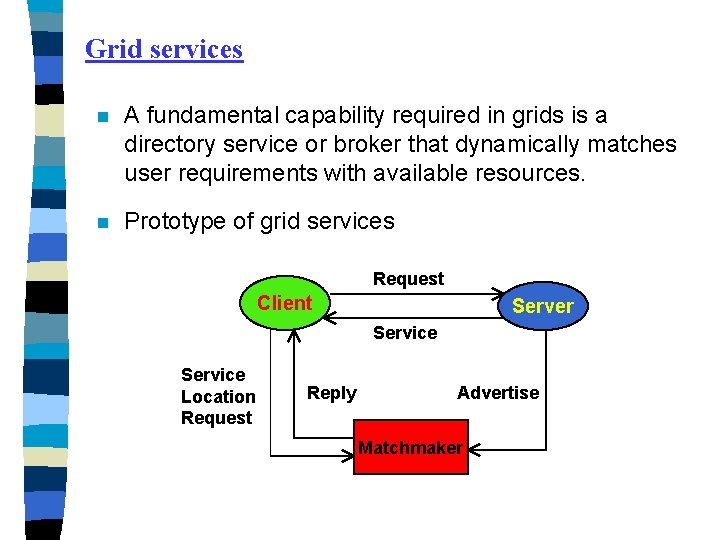
Grid services n A fundamental capability required in grids is a directory service or broker that dynamically matches user requirements with available resources. n Prototype of grid services Request Client Server Service Location Request Reply Advertise Matchmaker

Matching conflicts n Brokers and matchmakers use keywords and domain ontologies to specify services. n Keywords and ontologies cannot be defined and interpreted precisely enough to make brokering or matchmaking between grid services robust in a truly distributed, heterogeneous computing environment. n Matching conflicts exist between client’s requested functionality and service provider’s actual functionality.

An example n A client requires a three-dimensional FFT. A request is made to a broker or matchmaker for a FFT service based on the keywords and possibly parameter lists. n The broker or matchmaker uses the keywords to retrieve its catalog of services and returns with the candidate remote services. n Literally dozens of different algorithms for FFT computations with different assumptions, dimensions, accuracy, input-output format and so on. n The client must validate the actual functionality of these remote services before the client commits to use it.

Functional validation n n Functional validation means that a client presents to a prospective service provider a sequence of challenges. The service provider replies to these challenges with corresponding answers. Only after the client is satisfied that the service provider’s answers are consistent with the client’s expectations is an actual commitment made to using the service. Three steps: – Service identification and location. – Service functional validation. – Commitment to the service

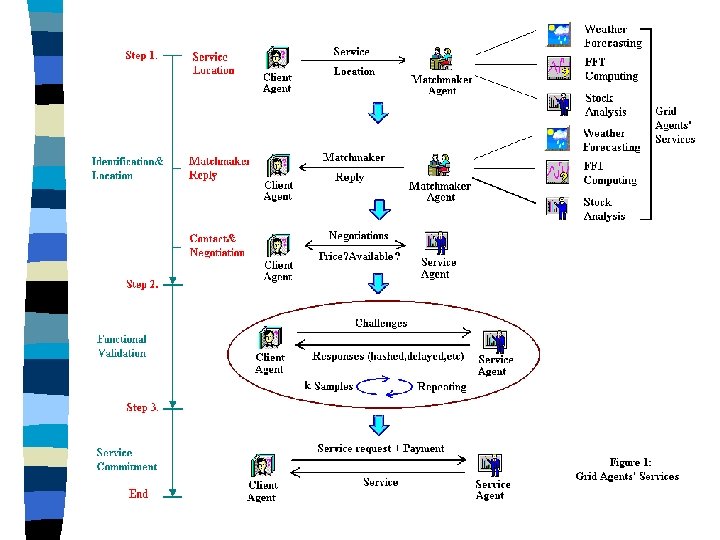
Our approach n Challenge the service provider with some test cases x 1, x 2, . . . , xk. The remote service provider R offers the corresponding answers f. R(x 1), f. R(x 2), . . . , f. R(xk). The client C may or may not have independent access to the answers f. C(x 1), f. C(x 2), . . . , f. C(xk). n Possible situations and machine learning models: – C “knows” f. C(x) and R provides f. R(x). • PAC learning and Chernoff bounds theory – C “knows” f. C(x) and R does not provide f. R(x). • Zero-knowledge proof – C does not “know” f. C(x) and R provides f. R(x). • Simulation-based learning and reinforcement learning

Mathematical framework n The goal of PAC learning is to use few examples as possible, and as little computation as possible to pick a hypothesis concept which is a close approximation to the target concept. n Define a concept to be a boolean mapping. X is the input space. c(x)=1 indicates x is a positive example , i. e. the service provider can offer the “correct” service for challenge x. n Define an index function n Now define the error between the target concept c and the hypothesis h as.

Mathematical framework(cont’d) n The client can randomly pick m samples to PAC learn a hypothesis h about whether the service provider can offer the “correct” service. n Theorem 1(Blumer et. al. ) Let H be any hypothesis space of finite VC dimension d contained in , P be any probability distribution on X and the target concept c be any Borel set contained in X. Then for any , given the following m independent random examples of c drawn according to P , with probability at least , every hypothesis in H that is consistent with all of these examples has error at most.

Simplified results n Assuming that with regard to some concepts, all test cases have the same probability about whether the service provider can offer the “correct” service. n Theorem 2(Chernoff bounds): Consider independent identically distributed samples , from a Bernoulli distribution with expectation. Define the empirical estimate of based on these samples as Then for any the probability n , if the sample size. , then Corollary 2. 1: For the functional validation problem described above, given any , if the sample size , then the probability.

Simplified results(cont’d) n Given a target probability P, the client needs to know how many positive consecutive samples are required so that the next request to the service will be correct with probability P. n So probabilities n Formulate the sample size problem as the following nonlinear optimization problem: s. t. , and P have the following inequality: and

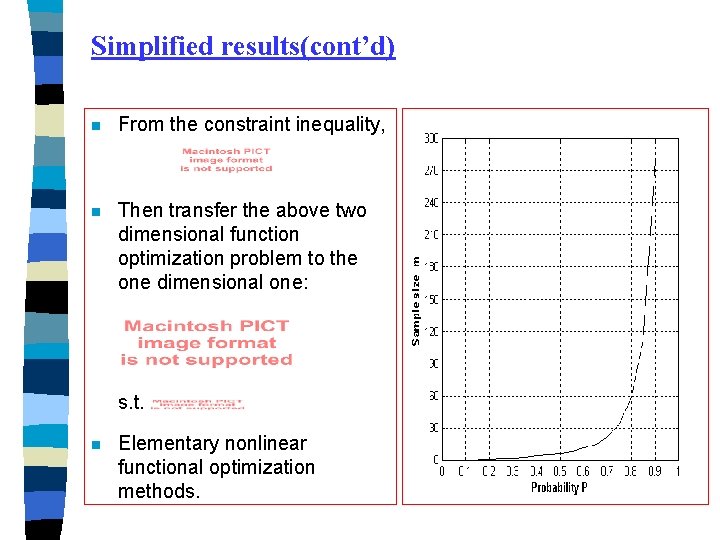
Simplified results(cont’d) n From the constraint inequality, n Then transfer the above two dimensional function optimization problem to the one dimensional one: s. t. n Elementary nonlinear functional optimization methods.

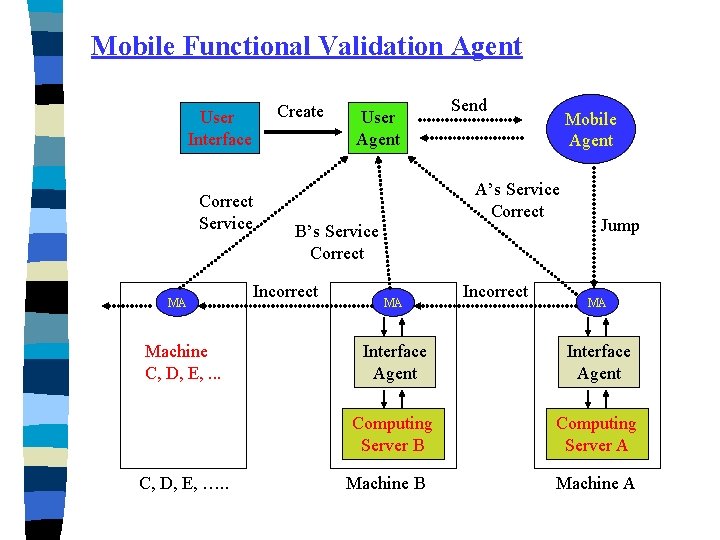
Mobile Functional Validation Agent User Interface Correct Service MA Machine C, D, E, . . . C, D, E, …. . Create User Agent Send Mobile Agent A’s Service Correct B’s Service Correct Incorrect MA Incorrect Jump MA Interface Agent Computing Server B Computing Server A Machine B Machine A

Future work and open questions n Integrate functional validation into grid computing infrastructure as a standard grid service. n Extend to other situations described(like zeroknowledge proofs, etc. ). n Formulate functional validation problems into more appropriate mathematical models. n Explore solutions for more difficult and complicated functional validation situations. n Thanks!!