Machine Learning and Data Mining via Mathematical Programming






























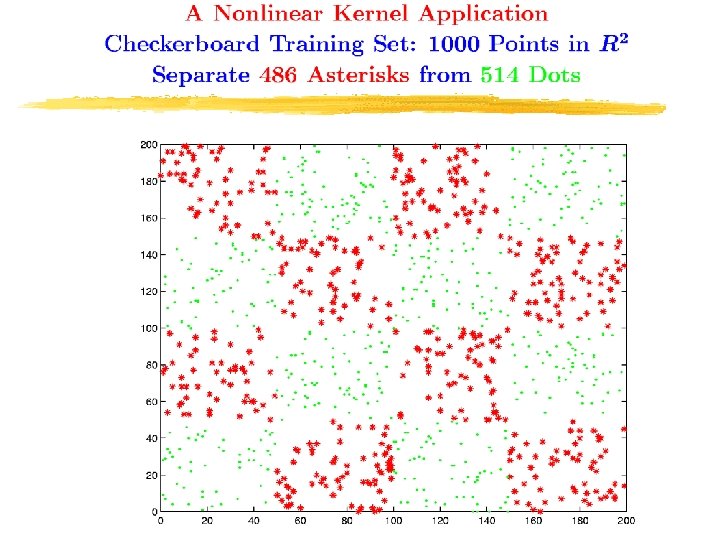



- Slides: 47

Machine Learning and Data Mining via Mathematical Programming Based Support Vector Machines Glenn M. Fung May 8, 2003 Ph. D. Dissertation Talk University of Wisconsin - Madison

Thesis Overview v Proximal support vector machines (PSVM) u Binary Classification u Multiclass Classification u Incremental Classification (massive datasets) v Knowledge based SVMs (KSVM) u Linear KSVM u Extension to Nonlinear KSVM v Sparse classifiers u Data selection for linear classifiers Ø Minimize # of support vectors u Minimal kernel classifiers u Feature selection Newton method for SVM. v Semi-Supervised SVMs v Finite Newton method for Lagrangian SVM classifiers

Outline of Talk v (Standard) Support vector machine (SVM) u Classify by halfspaces v Proximal support vector machine (PSVM) u Classify by proximity to planes v Incremental PSVM classifiers u Synthetic dataset consisting of 1 billion points in 10 dimensional input space classified in less than 2 hours and 26 minutes u. Knowledge based SVMs u Incorporate prior knowledge sets into classifiers v Minimal kernel classifiers v Reduce data dependence of nonlinear classifiers

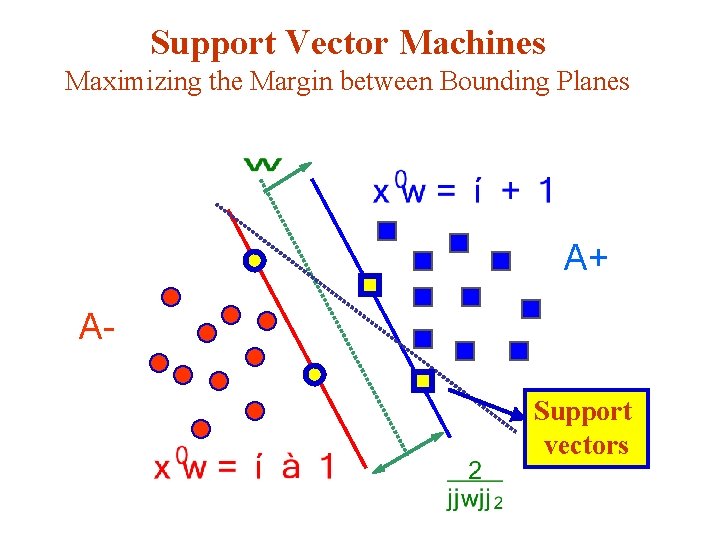
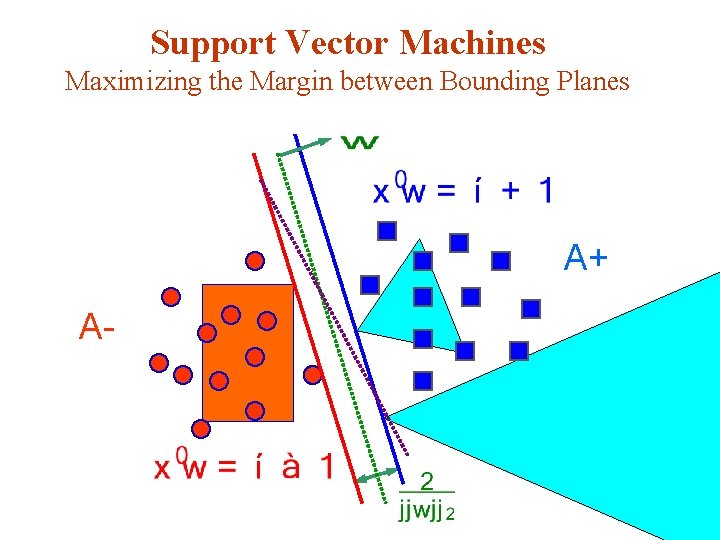
Support Vector Machines Maximizing the Margin between Bounding Planes A+ ASupport vectors

Standard Support Vector Machine Algebra of 2 -Category Linearly Separable Case v Given m points in n dimensional space v Represented by an m-by-n matrix A v Membership of each in class +1 or – 1 specified by: v An m-by-m diagonal matrix D with +1 & -1 entries v Separate by two bounding planes, v More succinctly: where e is a vector of ones.

Standard Support Vector Machine Formulation v Solve the quadratic program for some min (QP) s. t. where : , denotes or , membership. v Margin is maximized by minimizing

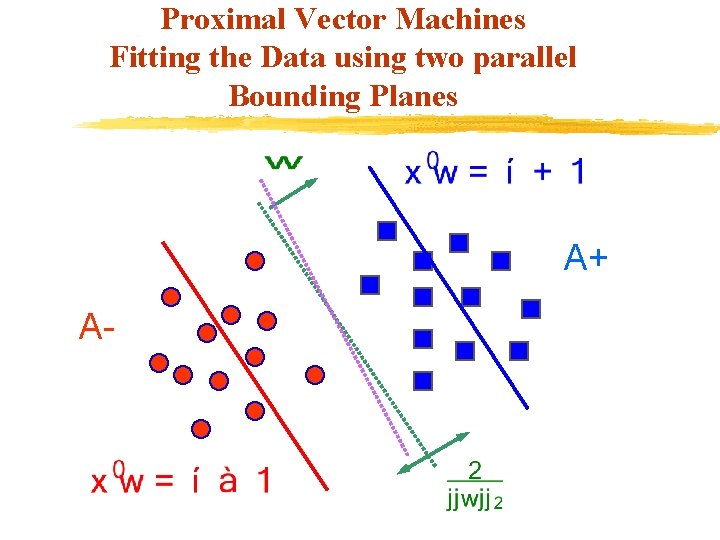
Proximal Vector Machines Fitting the Data using two parallel Bounding Planes A+ A-

PSVM Formulation We have from the QP SVM formulation: min (QP) s. t. Solving for in terms of and gives: min This simple, but critical modification, changes the nature of the optimization problem tremendously!!

Advantages of New Formulation v Objective function remains strongly convex v An explicit exact solution can be written in terms of the problem data v PSVM classifier is obtained by solving a single system of linear equations in the usually small dimensional input space v Exact leave-one-out-correctness can be obtained in terms of problem data

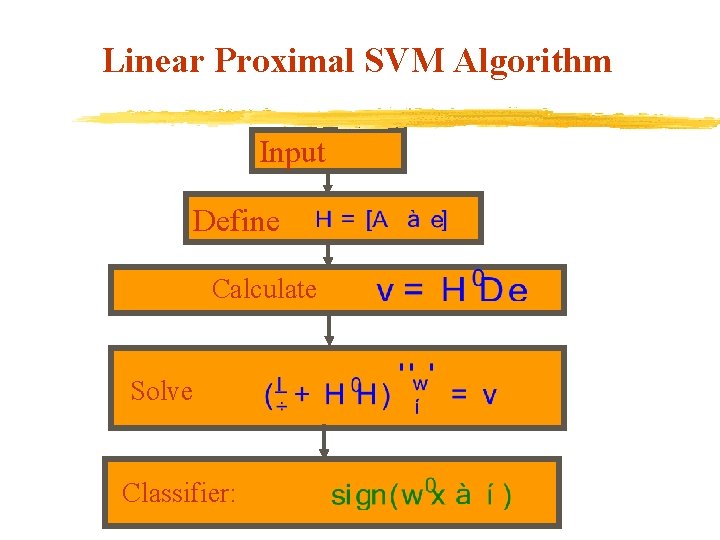
Linear PSVM We want to solve: min v. Setting the gradient equal to zero, gives a nonsingular system of linear equations. v. Solution of the system gives the desired PSVM classifier

Linear PSVM Solution Here, v The linear system to solve depends on: which is of the size v is usually much smaller than

Linear Proximal SVM Algorithm Input Define Calculate Solve Classifier:

Nonlinear PSVM Formulation v Linear PSVM: (Linear separating surface: min ) (QP) s. t. By QP “duality”, . Maximizing the margin in the “dual space” , gives: min v Replace min by a nonlinear kernel :

The Nonlinear Classifier v The nonlinear classifier: v Where K is a nonlinear kernel, e. g. : v Gaussian (Radial Basis) Kernel : Ø The -entry of of data points and represents the “similarity”

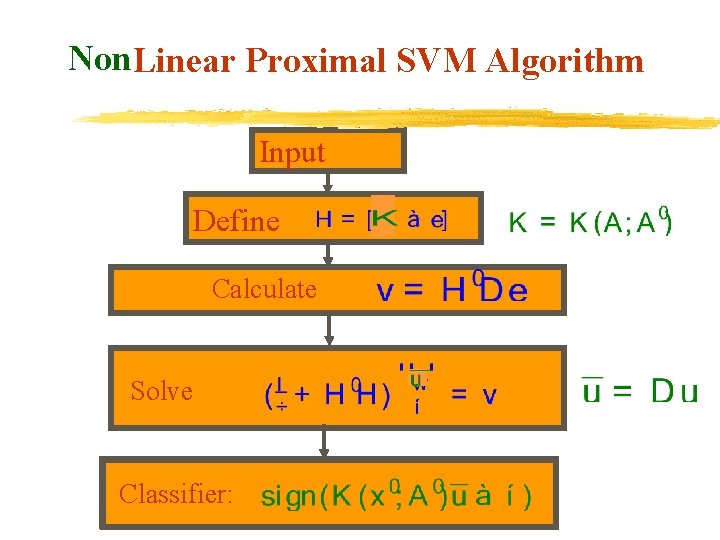
Nonlinear PSVM v Similar to the linear case, setting the gradient equal to zero, we obtain: Defining slightly different: v Here, the linear system to solve is of the size However, reduced kernel techniques can be used (RSVM) to reduce dimensionality.

Non. Linear Proximal SVM Algorithm Input Define Calculate Solve Classifier:

Incremental PSVM Classification v Suppose we have two “blocks” of data and v The linear system to solve depends on the compressed blocks: which are of the size

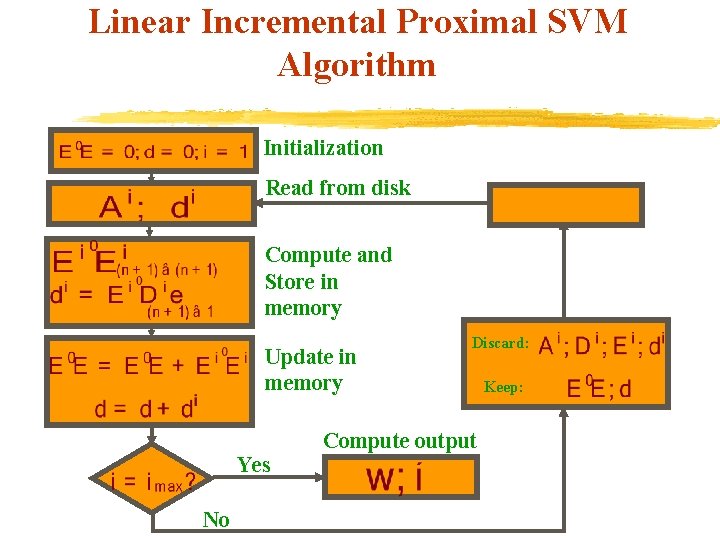
Linear Incremental Proximal SVM Algorithm Initialization Read from disk Compute and Store in memory Update in memory Yes No Discard: Compute output Keep:

Linear Incremental Proximal SVM Adding – Retiring Data v Capable of modifying an existing linear classifier by both adding and retiring data v Option of retiring old data is similar to adding new data u Financial Data: old data is obsolete v Option of keeping old data and merging it with the new data: u Medical Data: old data does not obsolesce.

Numerical experiments One-Billion Two-Class Dataset v Synthetic dataset consisting of 1 billion points in 10 dimensional input space v Generated by NDC (Normally Distributed Clustered) dataset generator v. Dataset divided into 500 blocks of 2 million points each. v. Solution obtained in less than 2 hours and 26 minutes v About 30% of the time was spent reading data from disk. v. Testing set correctness 90. 79%

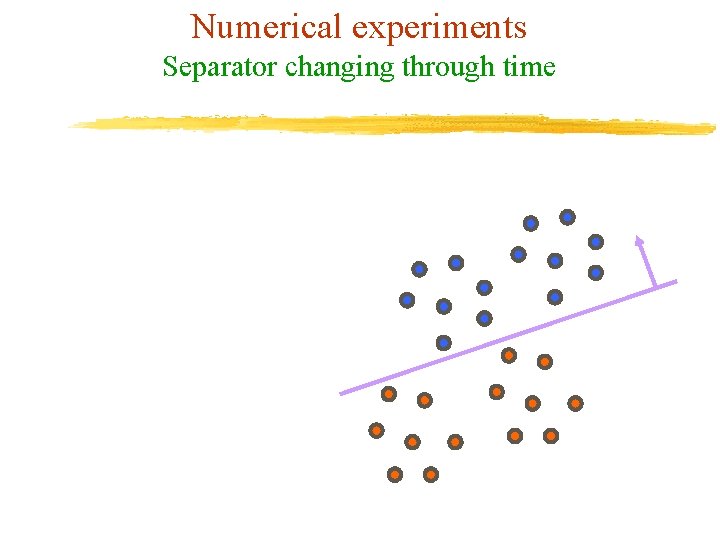
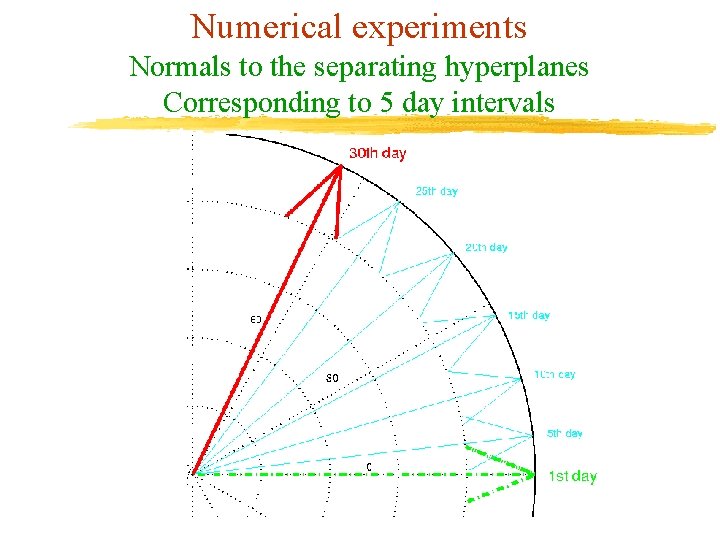
Numerical Experiments Simulation of Two-month 60 -Million Dataset v Synthetic dataset consisting of 60 million points (1 million per day) in 10 - dimensional input space v Generated using NDC v At the beginning, we only have data corresponding to the first month v Every day: u The oldest block of data is retired (1 Million) u A new block is added (1 Million) u A new linear classifier is calculated daily v Only an 11 by 11 matrix is kept in memory at the end of each day. All other data is purged.

Numerical experiments Separator changing through time

Numerical experiments Normals to the separating hyperplanes Corresponding to 5 day intervals

Support Vector Machines Linear Programming Formulation v Use the 1 -norm instead of the 2 -norm: min s. t. v This is equivalent to the following linear program: min s. t.

Support Vector Machines Maximizing the Margin between Bounding Planes A+ A-

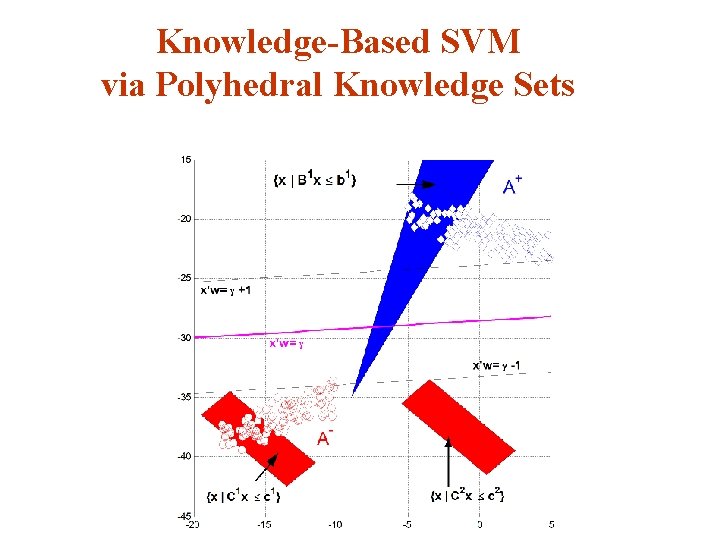
Incoporating Knowledge Sets Into an SVM Classifier v Suppose that the knowledge set: belongs to the class A+. Hence it must lie in the halfspace : v We therefore have the implication: v Will show that this implication is equivalent to a set of constraints that can be imposed on the classification problem.

Knowledge Set Equivalence Theorem

Knowledge-Based SVM Classification

Knowledge-Based SVM Classification v Adding one set of constraints for each knowledge set to the 1 -norm SVM LP, we have:

Knowledge-Based LP SVM with slack variables

Knowledge-Based SVM via Polyhedral Knowledge Sets

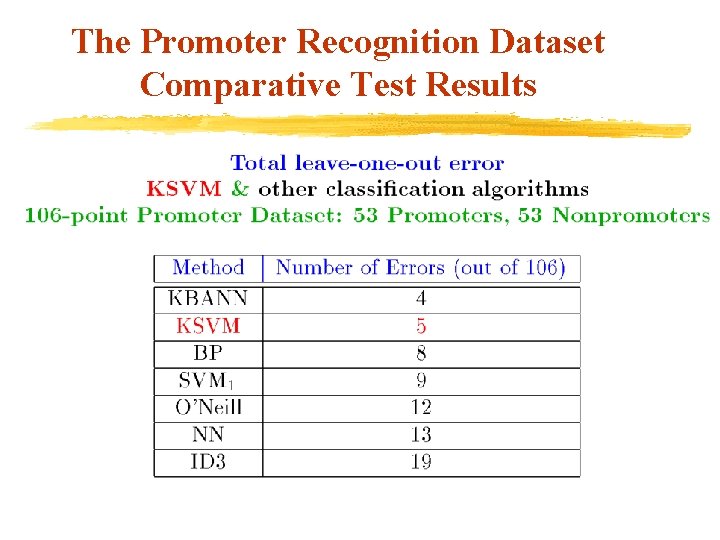
Numerical Testing The Promoter Recognition Dataset v Promoter: Short DNA sequence that precedes a gene sequence. v A promoter consists of 57 consecutive DNA nucleotides belonging to {A, G, C, T}. v Important to distinguish between promoters and nonpromoters v This distinction identifies starting locations of genes in long uncharacterized DNA sequences.

The Promoter Recognition Dataset Comparative Test Results

Minimal kernel Classifiers: Model Simplification v Goal #1: Generate a very sparse solution vector. u. Why? Minimizes number of kernel functions used. u Simplifies separating surface. u Reduces storage v Goal #2: Minimize number of active constraints. u. Why? Reduces data dependence. u Useful for massive incremental classification.

Model Simplification Goal #1 Simplifying Separating Surface v. The nonlinear separating surface: The separating surface does not depend explicitly on the datapoint v Minimize the number of nonzero

Model Simplification Goal #2 Minimize Data Dependence v By KKT conditions: Hence: v Minimize the number of nonzero

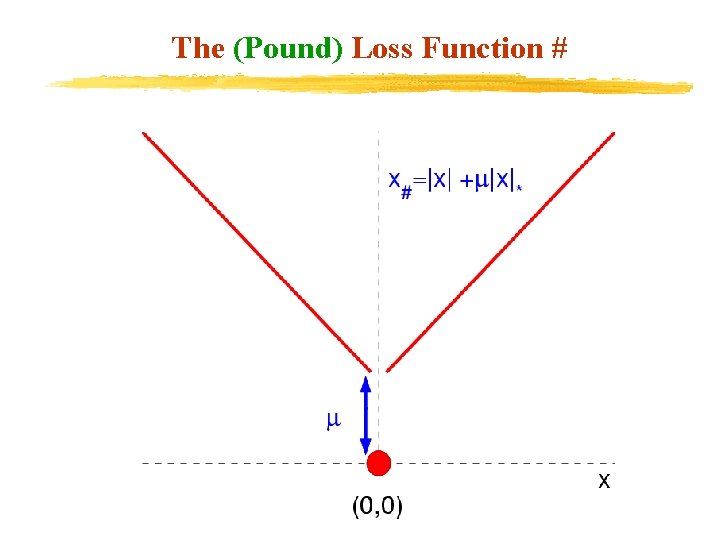
Achieving Model Simplification: Minimal Kernel Classifier Formulation min s. t. v Where is given by: v The new loss function # is given by:

The (Pound) Loss Function #

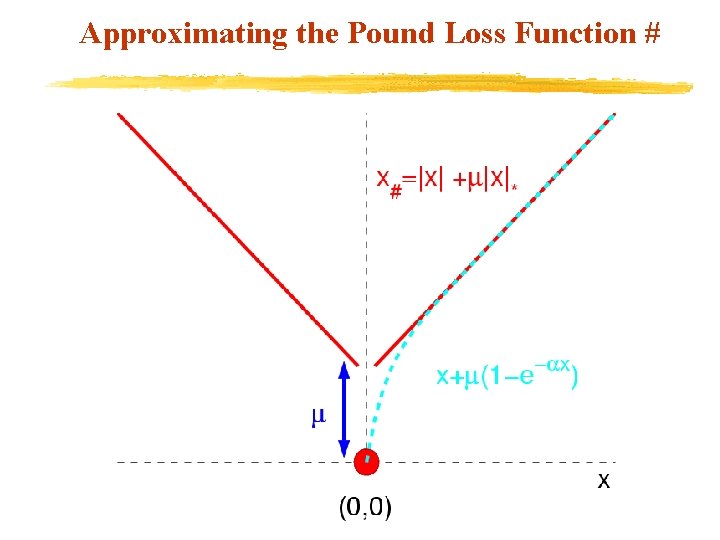
Approximating the Pound Loss Function #

Minimal Kernel Classifier as a Concave Minimization Problem min s. t. v For we have: v Problem can be effectively solved using the finite Successive Linearization Algorithm (SLA) (Mangasarian 1996)

Minimal Kernel Algorithm (SLA) v Start with: v Having by solving the LP: min s. t. v Stop when: determine

Minimal Kernel Algorithm (SLA) v Each iteration of the algorithm solves a Linear program. v. The algorithm terminates in a finite number of iterations (typically 5 to 7 iterations). v Solution obtained satisfies the Minimum Principle necessary optimality condition.


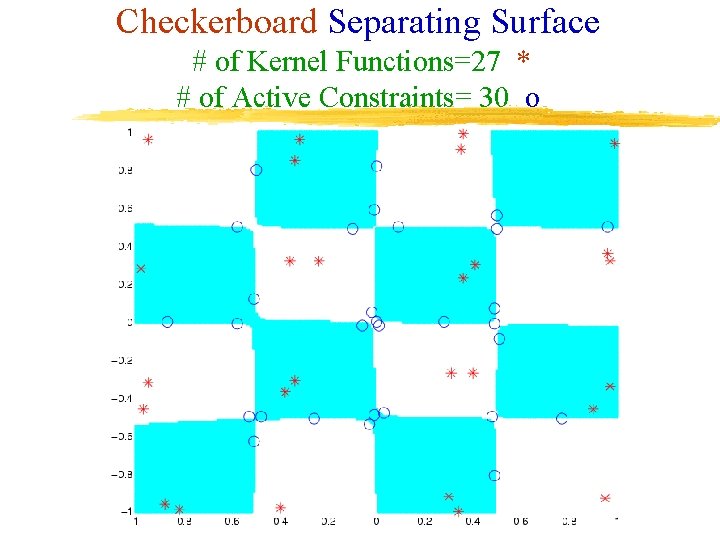
Checkerboard Separating Surface # of Kernel Functions=27 * # of Active Constraints= 30 o

Conclusions (PSVM) v PSVM is an extremely simple procedure for generating linear and nonlinear classifiers by solving a single system of linear equations v Comparable test set correctness to standard SVM v Much faster than standard SVMs : typically an order of magnitude less. v We also Proposed algorithm is an extremely simple procedure for generating linear classifiers in an incremental fashion for huge datasets. v The proposed algorithm has the ability to retire old data and add new data in a very simple manner. v Only a matrix of the size of the input space is kept in memory at any time.

Conclusions (KSVM) v Prior knowledge easily incorporated into classifiers through polyhedral knowledge sets. v Resulting problem is a simple LP. v Knowledge sets can be used with or without conventional labeled data. v In either case KSVM is better than most knowledge based classifiers.

Conclusions (Minimal Kernel Classifiers) v A finite algorithm that generates a classifier depending on a fraction of the input data only. u. Important for fast online testing of unseen data, e. g. fraud or intrusion detection. u. Useful for incremental training of massive data. v Overall algorithm consists of solving 5 to 7 LPs. v Kernel data dependence reduced up to 98. 8% of the data used by a standard SVM. u Testing time reduction up to: 98. 2%. v. MKC testing set correctness comparable to that of more complex standard SVM.