Machine Learning and Data Mining Linear regression adapted

+ Machine Learning and Data Mining Linear regression (adapted from) Prof. Alexander Ihler

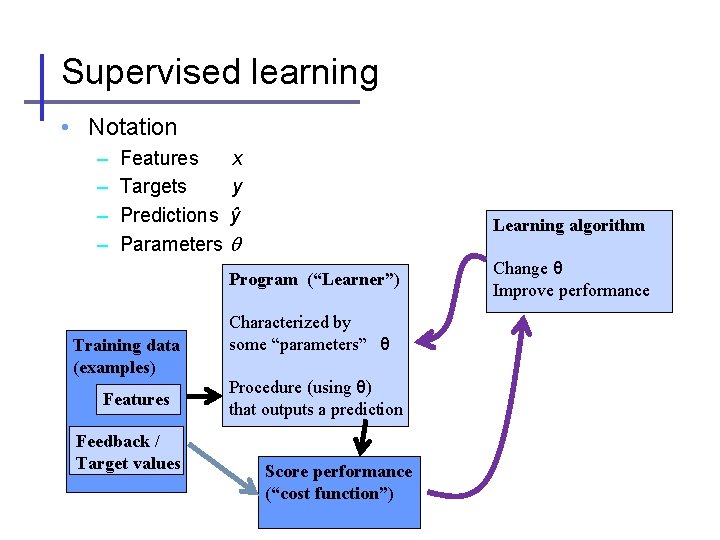
Supervised learning • Notation – – Features x Targets y Predictions ŷ Parameters q Learning algorithm Program (“Learner”) Training data (examples) Features Feedback / Target values Characterized by some “parameters” θ Procedure (using θ) that outputs a prediction Score performance (“cost function”) Change θ Improve performance

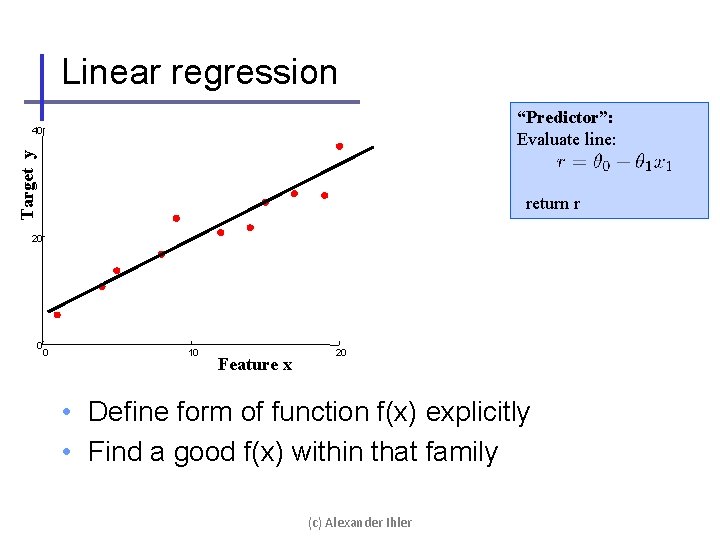
Linear regression “Predictor”: Evaluate line: Target y 40 return r 20 0 0 10 Feature x 20 • Define form of function f(x) explicitly • Find a good f(x) within that family (c) Alexander Ihler

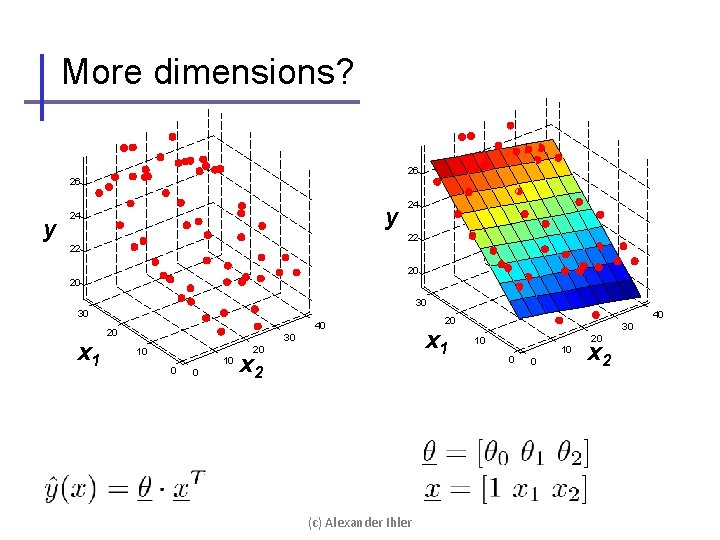
More dimensions? 26 26 y y 24 24 22 22 20 20 30 30 40 20 x 1 30 20 10 0 x 2 (c) Alexander Ihler 40 20 x 1 30 20 10 0 x 2

Notation Define “feature” x 0 = 1 (constant) Then (c) Alexander Ihler

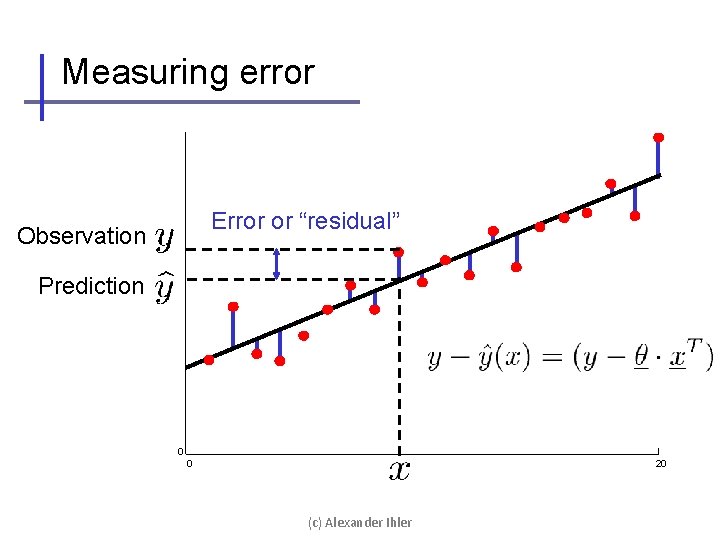
Measuring error Error or “residual” Observation Prediction 0 0 20 (c) Alexander Ihler

Mean squared error • How can we quantify the error? • Could choose something else, of course… – Computationally convenient (more later) – Measures the variance of the residuals – Corresponds to likelihood under Gaussian model of “noise” (c) Alexander Ihler

MSE cost function • Rewrite using matrix form (Matlab) >> e = y’ – th*X’; J = e*e’/m; (c) Alexander Ihler

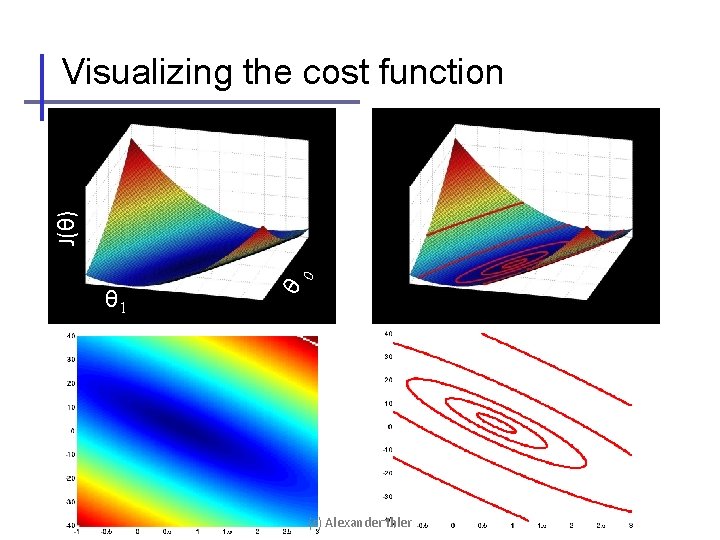
θ 1 θ 0 J(θ) Visualizing the cost function (c) Alexander Ihler

Supervised learning • Notation – – Features x Targets y Predictions ŷ Parameters q Learning algorithm Program (“Learner”) Training data (examples) Features Feedback / Target values Characterized by some “parameters” θ Procedure (using θ) that outputs a prediction Score performance (“cost function”) Change θ Improve performance

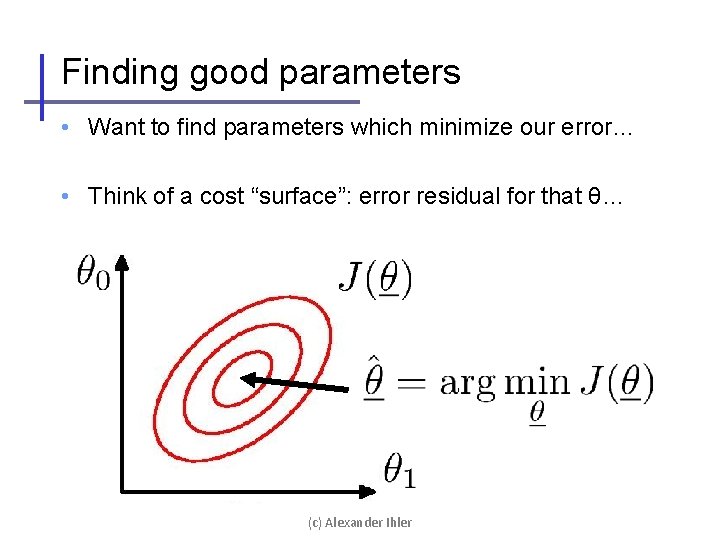
Finding good parameters • Want to find parameters which minimize our error… • Think of a cost “surface”: error residual for that θ… (c) Alexander Ihler

+ Machine Learning and Data Mining Linear regression: direct minimization (adapted from) Prof. Alexander Ihler

MSE Minimum • Consider a simple problem – One feature, two data points – Two unknowns: µ 0, µ 1 – Two equations: • Can solve this system directly: • However, most of the time, m > n – There may be no linear function that hits all the data exactly – Instead, solve directly for minimum of MSE function (c) Alexander Ihler

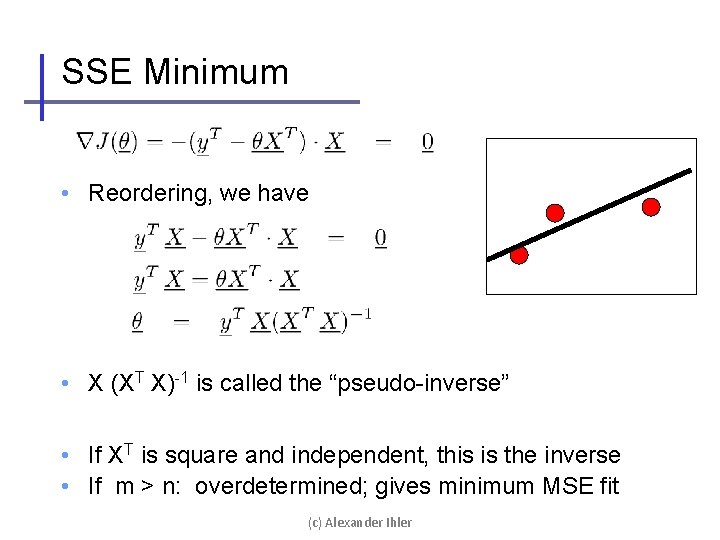
SSE Minimum • Reordering, we have • X (XT X)-1 is called the “pseudo-inverse” • If XT is square and independent, this is the inverse • If m > n: overdetermined; gives minimum MSE fit (c) Alexander Ihler

Matlab SSE • This is easy to solve in Matlab… % % y = [y 1 ; … ; ym] X = [x 1_0 … x 1_m ; x 2_0 … x 2_m ; …] % Solution 1: “manual” th = y’ * X * inv(X’ * X); % Solution 2: “mrdivide” th = y’ / X’; % th*X’ = y (c) Alexander Ihler => th = y/X’

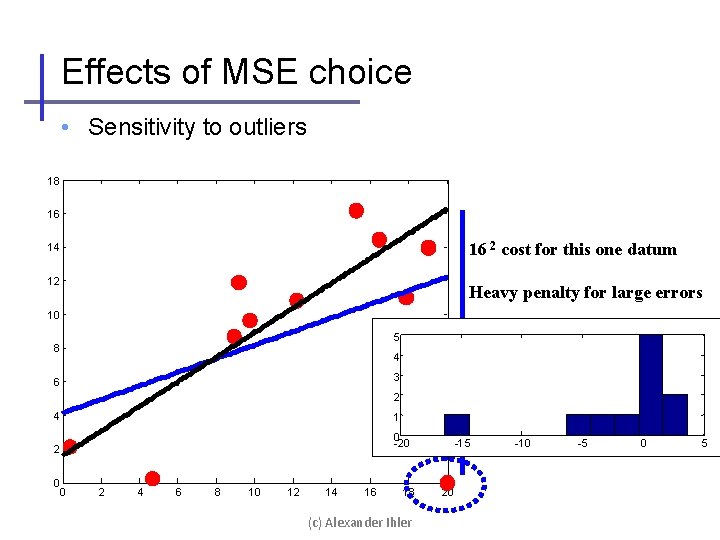
Effects of MSE choice • Sensitivity to outliers 18 16 16 2 cost for this one datum 14 12 Heavy penalty for large errors 10 5 8 4 3 6 2 4 1 0 -20 2 0 0 2 4 6 8 10 12 14 16 18 (c) Alexander Ihler -15 20 -10 -5 0 5

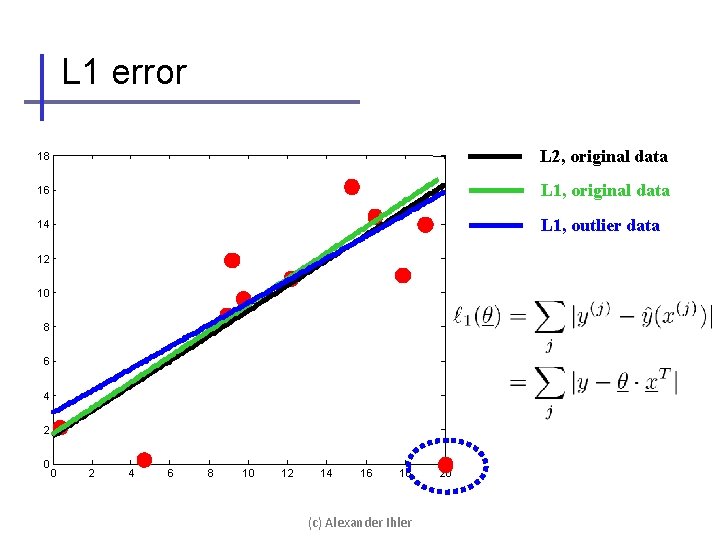
L 1 error 18 L 2, original data 16 L 1, original data 14 L 1, outlier data 12 10 8 6 4 2 0 0 2 4 6 8 10 12 14 16 18 (c) Alexander Ihler 20

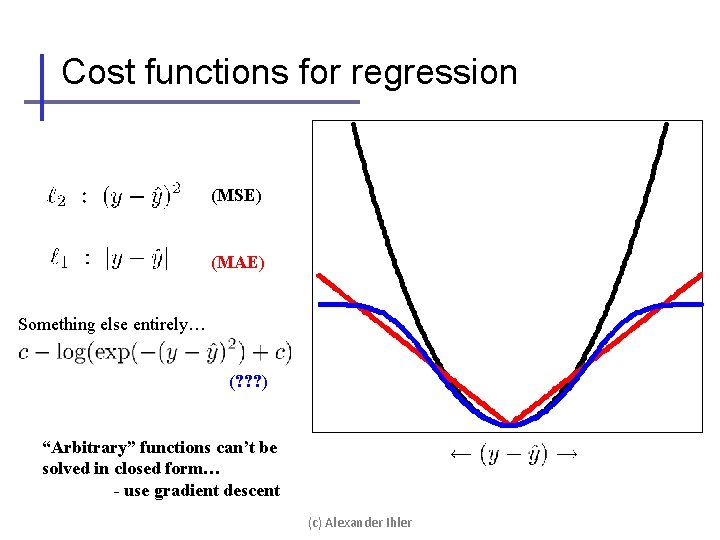
Cost functions for regression (MSE) (MAE) Something else entirely… (? ? ? ) “Arbitrary” functions can’t be solved in closed form… - use gradient descent (c) Alexander Ihler

+ Machine Learning and Data Mining Linear regression: nonlinear features (adapted from) Prof. Alexander Ihler

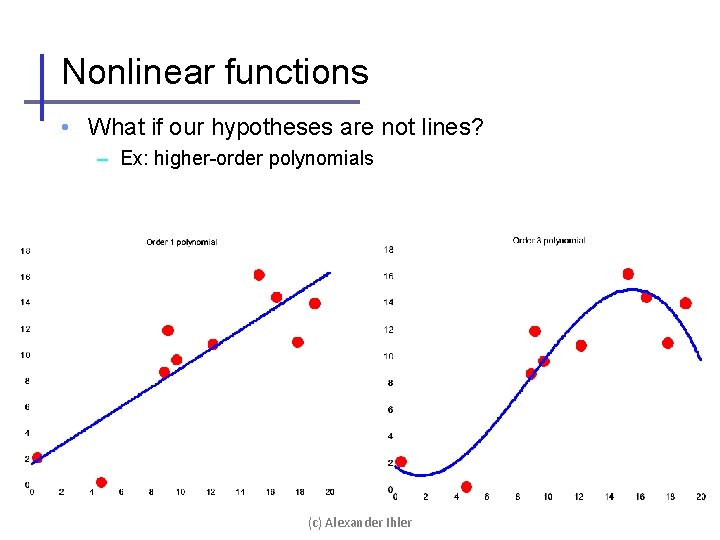
Nonlinear functions • What if our hypotheses are not lines? – Ex: higher-order polynomials (c) Alexander Ihler

Nonlinear functions • Single feature x, predict target y: Add features: Linear regression in new features • Sometimes useful to think of “feature transform” (c) Alexander Ihler

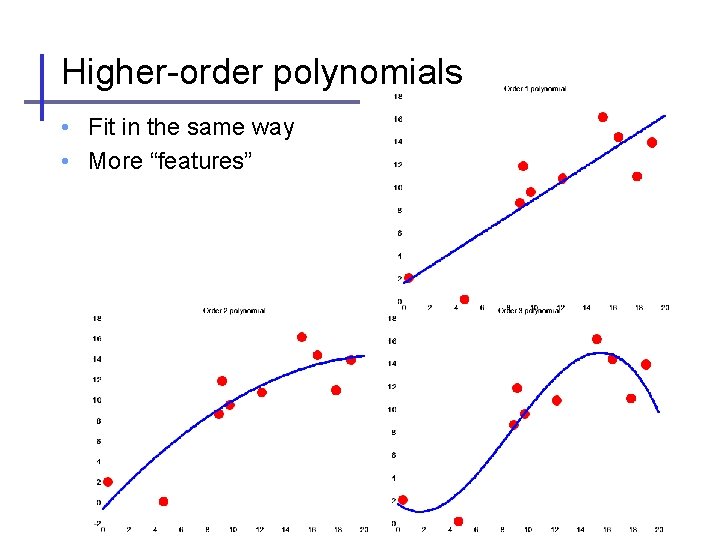
Higher-order polynomials • Fit in the same way • More “features”

Features • In general, can use any features we think are useful • Other information about the problem – Sq. footage, location, age, … • Polynomial functions – Features [1, x, x 2, x 3, …] • Other functions – 1/x, sqrt(x), x 1 * x 2, … • “Linear regression” = linear in the parameters – Features we can make as complex as we want! (c) Alexander Ihler

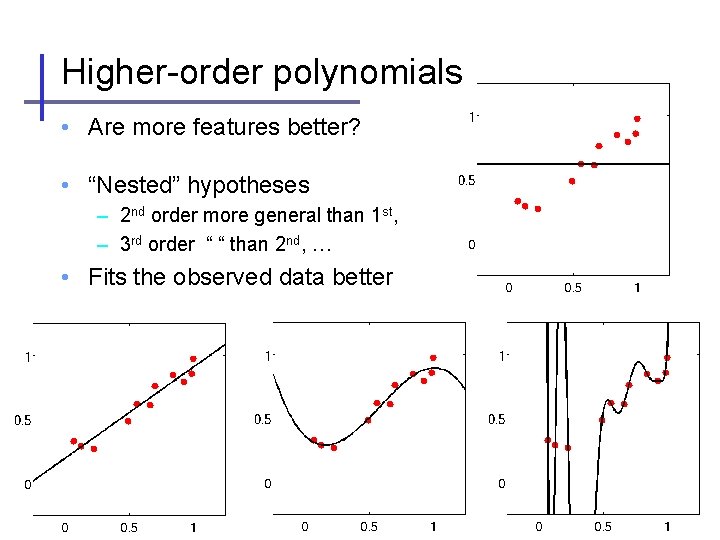
Higher-order polynomials • Are more features better? • “Nested” hypotheses – 2 nd order more general than 1 st, – 3 rd order “ “ than 2 nd, … • Fits the observed data better

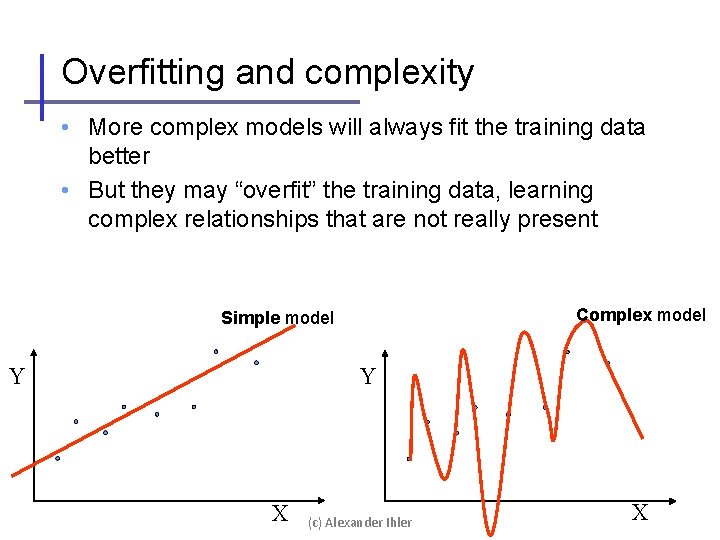
Overfitting and complexity • More complex models will always fit the training data better • But they may “overfit” the training data, learning complex relationships that are not really present Complex model Simple model Y Y X (c) Alexander Ihler X

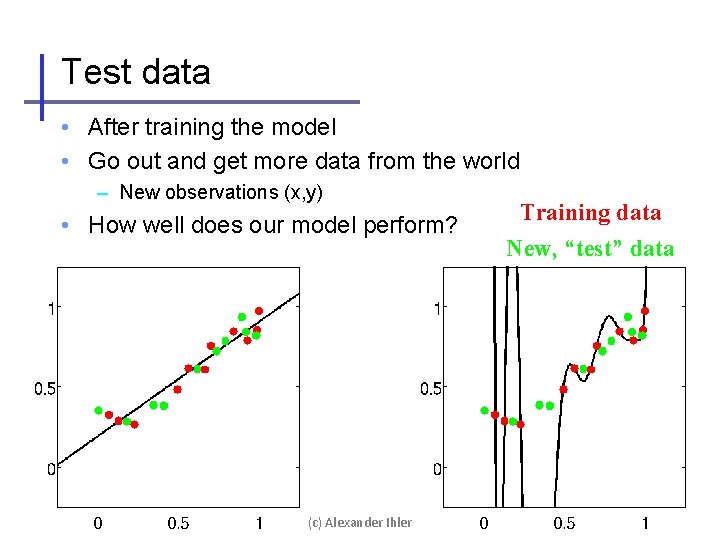
Test data • After training the model • Go out and get more data from the world – New observations (x, y) • How well does our model perform? (c) Alexander Ihler Training data New, “test” data

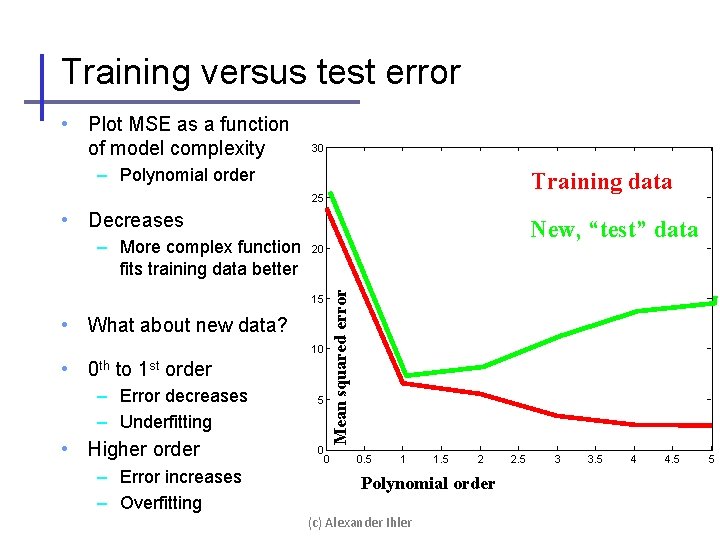
Training versus test error • Plot MSE as a function of model complexity 30 – Polynomial order Training data 25 • Decreases 20 15 • What about new data? 10 • 0 th to 1 st order – Error decreases – Underfitting • Higher order – Error increases – Overfitting 5 0 Mean squared error – More complex function fits training data better New, “test” data 0 0. 5 1 1. 5 2 Polynomial order (c) Alexander Ihler 2. 5 3 3. 5 4 4. 5 5