Machine Learning Algorithms and Theory of Approximate Inference

Machine Learning Algorithms and Theory of Approximate Inference Eric Xing Lecture 15, August 15, 2010 Reading: Eric Xing © Eric Xing @ CMU, 2006 -2010

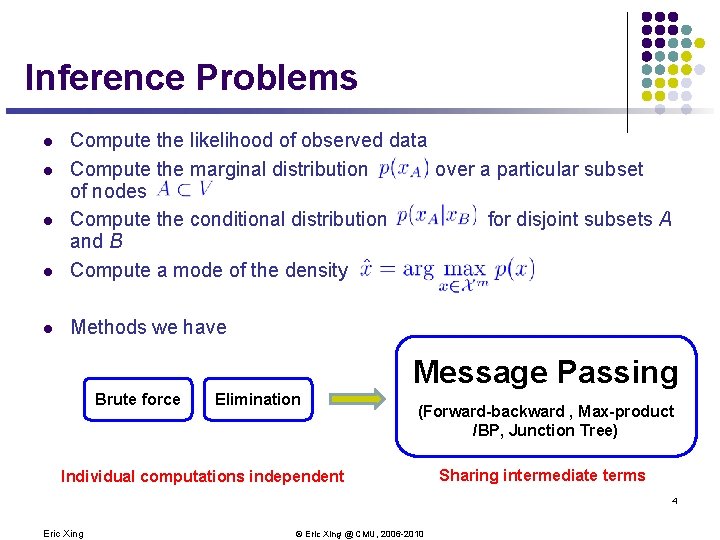
Inference Problems l l Compute the likelihood of observed data Compute the marginal distribution over a particular subset of nodes Compute the conditional distribution for disjoint subsets A and B Compute a mode of the density 2 Eric Xing © Eric Xing @ CMU, 2006 -2010

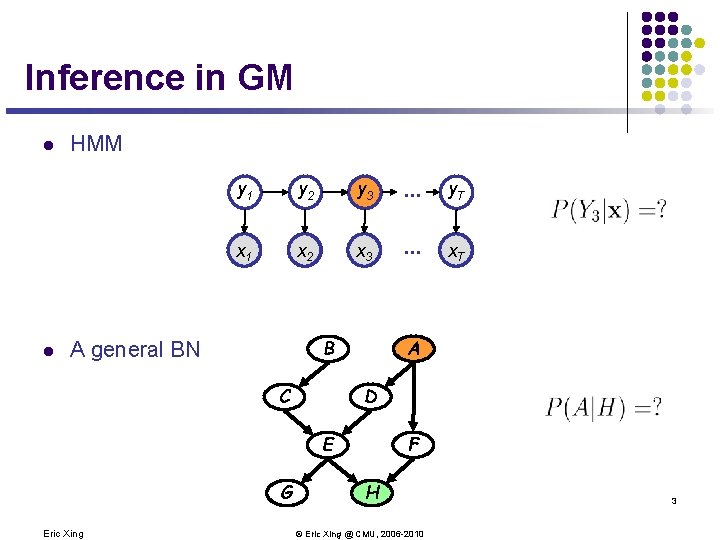
Inference in GM l l HMM y 1 y 2 y 3 . . . y. T x. A 1 x. A 2 x. A 3 . . . x. AT A B A general BN D C F E G Eric Xing H © Eric Xing @ CMU, 2006 -2010 3

Inference Problems l Compute the likelihood of observed data Compute the marginal distribution over a particular subset of nodes Compute the conditional distribution for disjoint subsets A and B Compute a mode of the density l Methods we have l l l Message Passing Brute force Elimination (Forward-backward , Max-product /BP, Junction Tree) Individual computations independent Sharing intermediate terms 4 Eric Xing © Eric Xing @ CMU, 2006 -2010

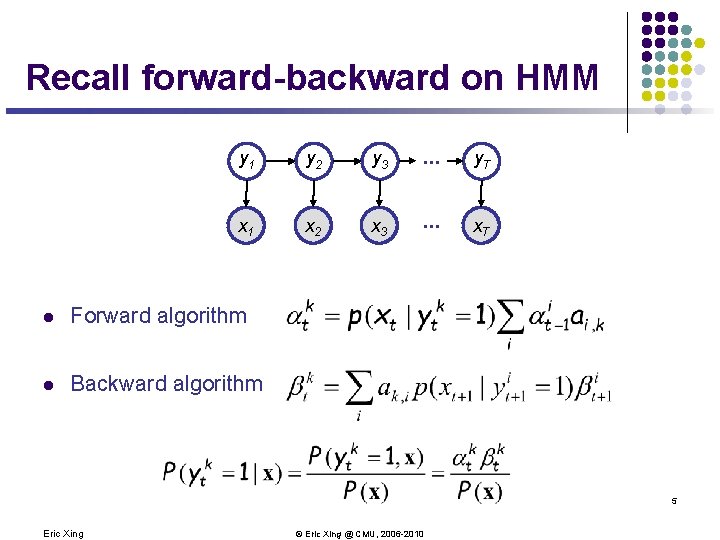
Recall forward-backward on HMM y 1 y 2 y 3 . . . y. T x. A 1 x. A 2 x. A 3 . . . x. AT l Forward algorithm l Backward algorithm 5 Eric Xing © Eric Xing @ CMU, 2006 -2010

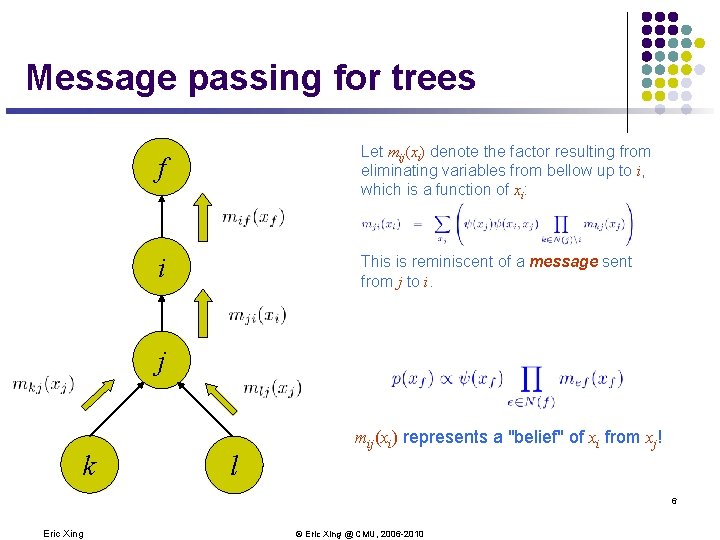
Message passing for trees f Let mij(xi) denote the factor resulting from eliminating variables from bellow up to i, which is a function of xi: i This is reminiscent of a message sent from j to i. j k l mij(xi) represents a "belief" of xi from xj! 6 Eric Xing © Eric Xing @ CMU, 2006 -2010

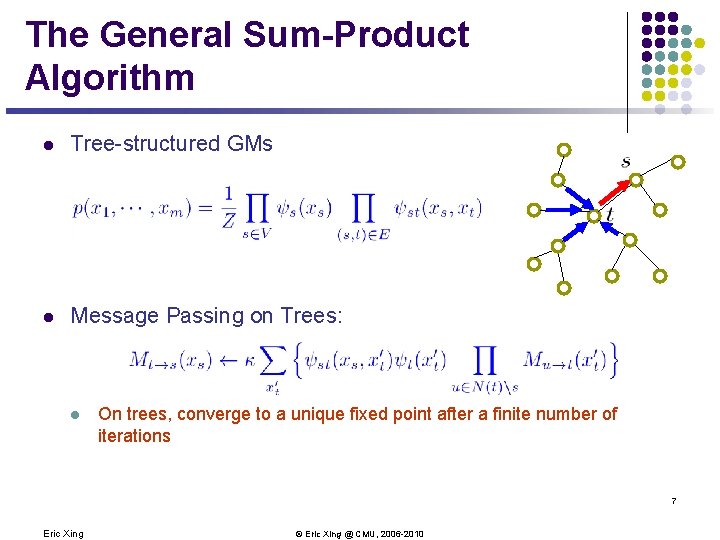
The General Sum-Product Algorithm l Tree-structured GMs l Message Passing on Trees: l On trees, converge to a unique fixed point after a finite number of iterations 7 Eric Xing © Eric Xing @ CMU, 2006 -2010

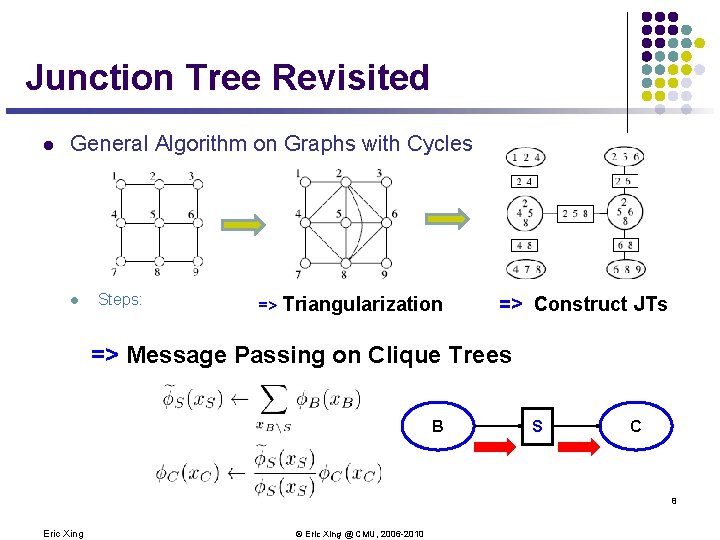
Junction Tree Revisited l General Algorithm on Graphs with Cycles l Steps: => Triangularization => Construct JTs => Message Passing on Clique Trees B S C 8 Eric Xing © Eric Xing @ CMU, 2006 -2010

Local Consistency l Given a set of functions with the cliques and separator sets associated l They are locally consistent if: l For junction trees, local consistency is equivalent to global consistency! 9 Eric Xing © Eric Xing @ CMU, 2006 -2010

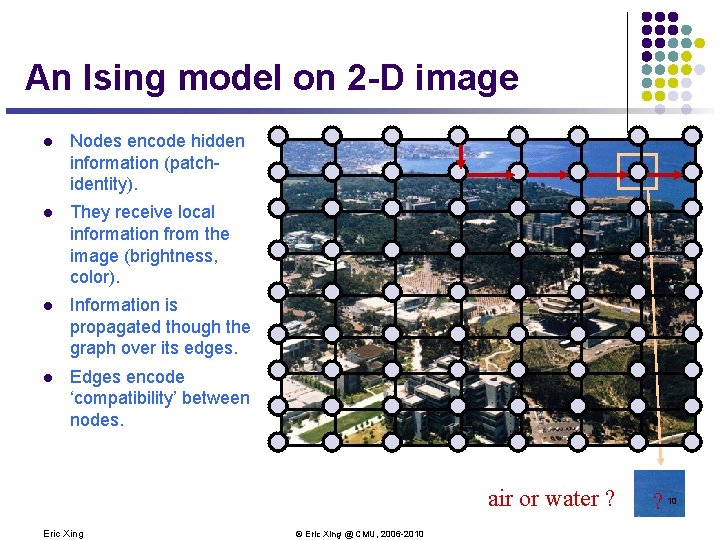
An Ising model on 2 -D image l Nodes encode hidden information (patchidentity). l They receive local information from the image (brightness, color). l Information is propagated though the graph over its edges. l Edges encode ‘compatibility’ between nodes. air or water ? Eric Xing © Eric Xing @ CMU, 2006 -2010 ? 10

Why Approximate Inference? l Why can’t we just run junction tree on this graph? l If Nx. N grid, tree width at least N l N can be a huge number(~1000 s of pixels) l Eric Xing If N~O(1000), we have a clique with 2100 entries © Eric Xing @ CMU, 2006 -2010 11

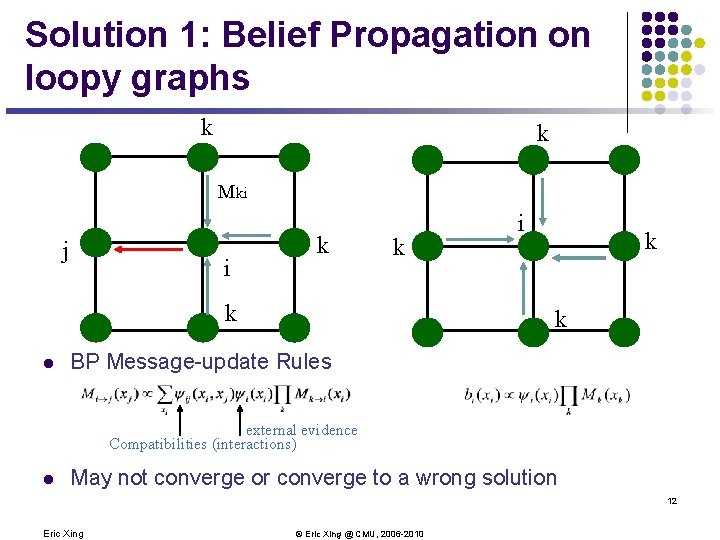
Solution 1: Belief Propagation on loopy graphs k k Mki j i k k k l i k k BP Message-update Rules external evidence Compatibilities (interactions) l May not converge or converge to a wrong solution 12 Eric Xing © Eric Xing @ CMU, 2006 -2010

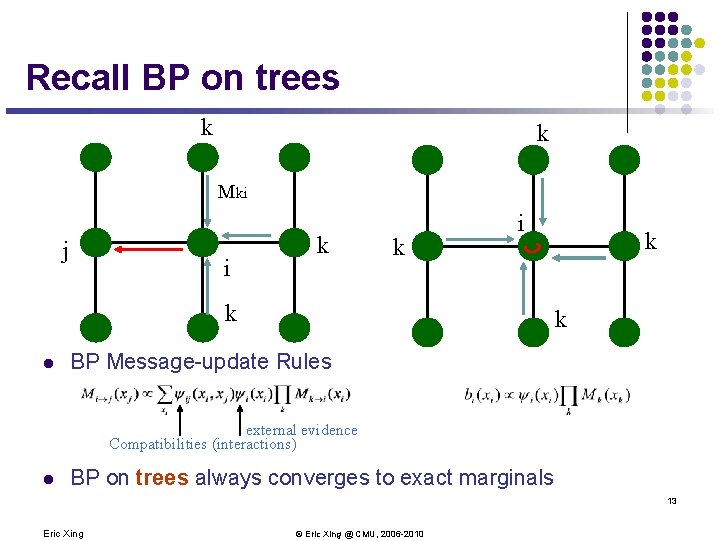
Recall BP on trees k k Mki j i k k i k l k k BP Message-update Rules external evidence Compatibilities (interactions) l BP on trees always converges to exact marginals 13 Eric Xing © Eric Xing @ CMU, 2006 -2010

Solution 2: The naive mean field approximation l Approximate p(X) by fully factorized q(X)=Piqi(Xi) l For Boltzmann distribution p(X)=exp{åi < j qij. Xi. Xj+qio. Xi}/Z : mean field equation: Xi § Áxjñq resembles a “message” sent from node j to i j § {áxjñq : j Î Ni} j Eric Xing forms the “mean field” applied to Xi from its neighborhood 14 © Eric Xing @ CMU, 2006 -2010

Recall Gibbs sampling l Approximate p(X) by fully factorized q(X)=Piqi(Xi) l For Boltzmann distribution p(X)=exp{åi < j qij. Xi. Xj+qio. Xi}/Z : Gibbs predictive distribution: Xi 15 Eric Xing © Eric Xing @ CMU, 2006 -2010

Summary So Far l Exact inference methods are limited to tree-structured graphs l Junction Tree methods is exponentially expensive to the treewidth l Message Passing methods can be applied for loopy graphs, but lack of analysis! l Mean-field is convergent, but can have local optimal l Where do these two algorithm come from? Do they make 16 sense? Eric Xing © Eric Xing @ CMU, 2006 -2010

Next Step … l Develop a general theory of variational inference l Introduce some approximate inference methods l Provide deep understandings to some popular methods 17 Eric Xing © Eric Xing @ CMU, 2006 -2010

Exponential Family GMs l Canonical Parameterization Canonical Parameters Sufficient Statistics Log-normalization Function l Effective canonical parameters l Regular family: l Minimal representation: l if there does not exist a nonzero vector constant such that is a 18 Eric Xing © Eric Xing @ CMU, 2006 -2010

Examples l Ising Model (binary r. v. : {-1, +1}) l Gaussian MRF 19 Eric Xing © Eric Xing @ CMU, 2006 -2010

Mean Parameterization l The mean parameter associated with a sufficient statistic is defined as l Realizable mean parameter set l A convex subset of Convex hull for discrete case l Convex polytope when l is finite 20 Eric Xing © Eric Xing @ CMU, 2006 -2010

Convex Polytope l Convex hull representation l Half-plane based representation l Minkowski-Weyl Theorem: l any polytope can be characterized by a finite collection of linear inequality constraints 21 Eric Xing © Eric Xing @ CMU, 2006 -2010

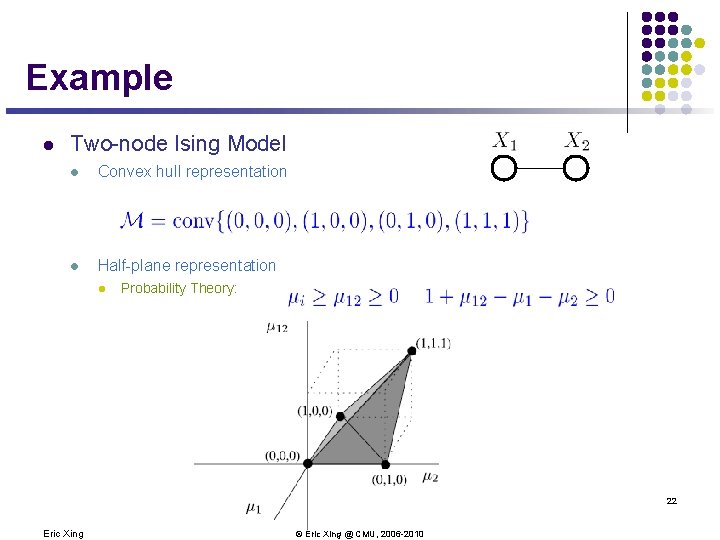
Example l Two-node Ising Model l Convex hull representation l Half-plane representation l Probability Theory: 22 Eric Xing © Eric Xing @ CMU, 2006 -2010

Marginal Polytope l Canonical Parameterization l Mean parameterization l Marginal distributions over nodes and edges l Marginal Polytope 23 Eric Xing © Eric Xing @ CMU, 2006 -2010

Conjugate Duality l l Duality between MLE and Max-Ent: l For all , a unique canonical parameter satisfying l The log-partition function has the variational form l For all , the supremum in (*) is attained uniquely at moment-matching conditions specified by the Bijection for minimal exponential family 24 Eric Xing © Eric Xing @ CMU, 2006 -2010

Roles of Mean Parameters l l Forward Mapping: l From to the mean parameters l A fundamental class of inference problems in exponential family models Backward Mapping: l Parameter estimation to learn the unknown 25 Eric Xing © Eric Xing @ CMU, 2006 -2010

Example l Bernoulli l If Unique! No gradient stationary point in the Opt. problem (**) l Reverse mapping: Unique! Eric Xing © Eric Xing @ CMU, 2006 -2010 26

Variational Inference In General l An umbrella term that refers to various mathematical tools for optimization-based formulations of problems, as well as associated techniques for their solution l General idea: l Express a quantity of interest as the solution of an optimization problem l The optimization problem can be relaxed in various ways l l l Approximate the functions to be optimized Approximate the set over which the optimization takes place Goes in parallel with MCMC 27 Eric Xing © Eric Xing @ CMU, 2006 -2010

A Tree-Based Outer-Bound to a l l Local Consistent (Pseudo-) Marginal Polytope l normalization l marginalization Relation to l holds for any graph l holds for tree-structured graphs 28 Eric Xing © Eric Xing @ CMU, 2006 -2010

A l Example A three node graph (binary r. v. ) 1 3 l For any l For l 2 , we have an exercise? 29 Eric Xing © Eric Xing @ CMU, 2006 -2010

Bethe Entropy Approximation l Approximate the negative entropy , which doesn’t has a closed-form in general graph. l Entropy on tree (Marginals) l l recall: l entropy Bethe entropy approximation (Pseudo-marginals) 30 Eric Xing © Eric Xing @ CMU, 2006 -2010

Bethe Variational Problem (BVP) l l We already have: l a convex (polyhedral) outer bound l the Bethe approximate entropy Combining the two ingredients, we have l l a simple structured problem (differentiable & constraint set is a simple polytope) Max-product is the solver! 31 Nobel Prize in Physics (1967) Eric Xing © Eric Xing @ CMU, 2006 -2010

Connection to Sum-Product Alg. l Lagrangian method for BVP: l Sum-product and Bethe Variational (Yedidia et al. , 2002) l For any graph G, any fixed point of the sum-product updates specifies a pair of such that l For a tree-structured MRF, the solution is unique, where correspond to the exact singleton and pairwise marginal distributions of the MRF, and the optimal value of BVP is equal to 32 Eric Xing © Eric Xing @ CMU, 2006 -2010

Proof 33 Eric Xing © Eric Xing @ CMU, 2006 -2010

Discussions l The connection provides a principled basis for applying the sum-product algorithm for loopy graphs l However, l l this connection provides no guarantees on the convergence of the sum-product alg. on loopy graphs l the Bethe variational problem is usually non-convex. Therefore, there are no guarantees on the global optimum l Generally, there are no guarantees that is a lower bound of However, however l the connection and understanding suggest a number of avenues for improving upon the ordinary sum-product alg. , via progressively better approximations to the entropy function and outer bounds on the marginal polytope! 34 Eric Xing © Eric Xing @ CMU, 2006 -2010

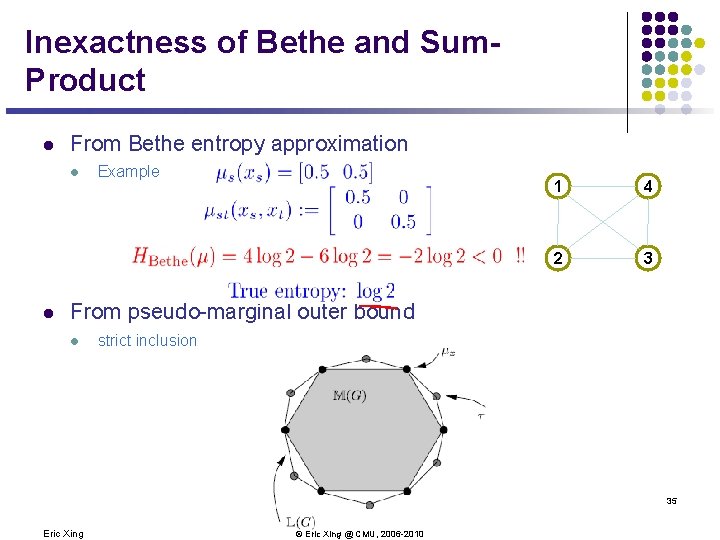
Inexactness of Bethe and Sum. Product l From Bethe entropy approximation l l Example 1 4 2 3 From pseudo-marginal outer bound l strict inclusion 35 Eric Xing © Eric Xing @ CMU, 2006 -2010

Summary of LBP l Variational methods in general turn inference into an optimization problem l However, both the objective function and constraint set are hard to deal with l Bethe variational approximation is a tree-based approximation to both objective function and marginal polytope l Belief propagation is a Lagrangian-based solver for BVP l Generalized BP extends BP to solve the generalized hyper-tree based variational approximation problem 36 Eric Xing © Eric Xing @ CMU, 2006 -2010

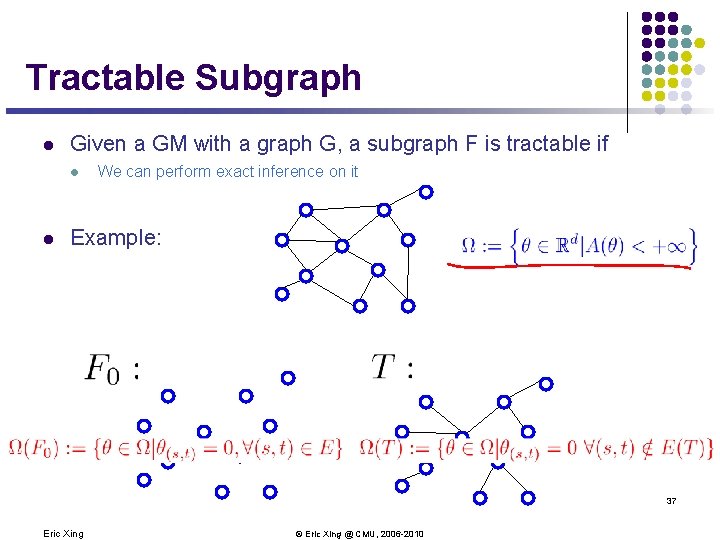
Tractable Subgraph l Given a GM with a graph G, a subgraph F is tractable if l l We can perform exact inference on it Example: 37 Eric Xing © Eric Xing @ CMU, 2006 -2010

Mean Parameterization l For an exponential family GM defined with graph G and sufficient statistics , the realizable mean parameter set l For a given tractable subgraph F, a subset of mean parameters is of interest l Inner Approximation 38 Eric Xing © Eric Xing @ CMU, 2006 -2010

Optimizing a Lower Bound l Any mean parameter partition function l yields a lower bound on the log- Moreover, equality holds iff and l Proof Idea: (Jensen’s Inequality) l Optimizing the lower bound gives l are dually coupled, i. e. , This is an inference! 39 Eric Xing © Eric Xing @ CMU, 2006 -2010

Mean Field Methods In General l However, the lower bound can’t explicitly evaluated in general l l Because the dual function typically lacks an explicit form Mean Field Methods l Approximate the lower bound l Approximate the realizable mean parameter set l The MF optimization problem l Still a lower bound? 40 Eric Xing © Eric Xing @ CMU, 2006 -2010

KL-divergence l Kullback-Leibler Divergence l For two exponential family distributions with the same STs: Primal Form Mixed Form Dual Form 41 Eric Xing © Eric Xing @ CMU, 2006 -2010

Mean Field and KL-divergence l Optimizing a lower bound l Equivalent to minimize a KL-divergence l Therefore, we are doing minimization 42 Eric Xing © Eric Xing @ CMU, 2006 -2010

Naïve Mean Field l Fully factorized variational distribution 43 Eric Xing © Eric Xing @ CMU, 2006 -2010

Naïve Mean Field for Ising Model l Sufficient statistics and Mean Parameters l Naïve Mean Field l Realizable mean parameter subset l Entropy l Optimization Problem 44 Eric Xing © Eric Xing @ CMU, 2006 -2010

Naïve Mean Field for Ising Model l Optimization Problem l Update Rule resembles “message” sent from node l l neighborhood forms the “mean field” applied to to from its 45 Eric Xing © Eric Xing @ CMU, 2006 -2010

Non-Convexity of Mean Field l Mean field optimization is always non-convex for any exponential family in which the state space is finite l Finite convex hull contains all the extreme points l l l If is a convex set, then Mean field has been used successfully 46 Eric Xing © Eric Xing @ CMU, 2006 -2010

Structured Mean Field l Mean field theory is general to any tractable sub-graphs l Naïve mean field is based on the fully unconnected sub-graph l Variants based on structured sub-graphs can be derived 47 Eric Xing © Eric Xing @ CMU, 2006 -2010

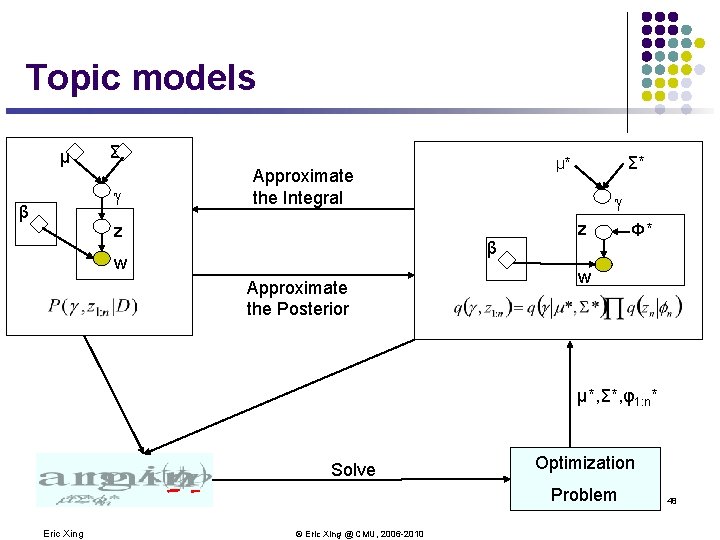
Topic models μ Σ g β z g β w Approximate the Posterior Σ* μ* Approximate the Integral z Φ* w μ*, Σ*, φ1: n* Solve Optimization Problem Eric Xing © Eric Xing @ CMU, 2006 -2010 48

Variational Inference With no Tears [Ahmed and Xing, 2006, Xing et al 2003] μ l Fully Factored Distribution Σ g z β e l Fixed Point Equations μ Σ g β z e Laplace approximation 49 Eric Xing © Eric Xing @ CMU, 2006 -2010

Summary of GMF l Message-passing algorithms (e. g. , belief propagation, mean field) are solving approximate versions of exact variational principle in exponential families l There are two distinct components to approximations: l Can use either inner or outer bounds to l Various approximation to the entropy function l BP: polyhedral outer bound and non-convex Bethe approximation l MF: non-convex inner bound and exact form of entropy l Kikuchi: tighter polyhedral outer bound and better entropy approximation 50 Eric Xing © Eric Xing @ CMU, 2006 -2010 2005 -2009