Machine interference problem introduction 1 N machines 1

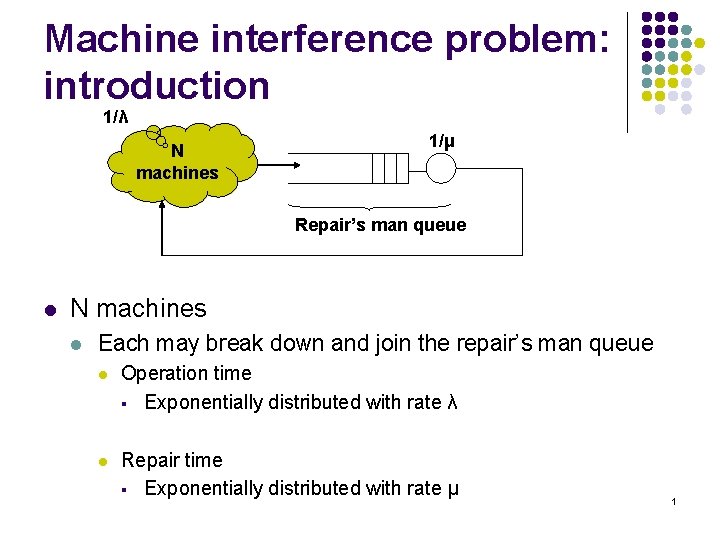
Machine interference problem: introduction 1/λ N machines 1/μ Repair’s man queue l N machines l Each may break down and join the repair’s man queue l Operation time § Exponentially distributed with rate λ l Repair time § Exponentially distributed with rate μ 1

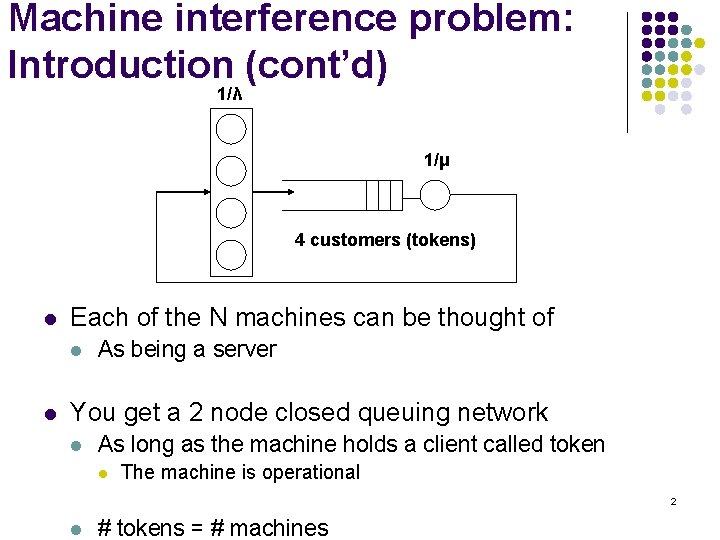
Machine interference problem: Introduction (cont’d) 1/λ 1/μ 4 customers (tokens) l Each of the N machines can be thought of l l As being a server You get a 2 node closed queuing network l As long as the machine holds a client called token l The machine is operational 2 l # tokens = # machines

Machine interference problem: history l Early computer systems l l Multiple terminals sharing a computer (CPU) l Jobs are shifted to the computer l Jobs run according to a Time Sharing idea Main performance issue l l How many terminals can I support so that § Response time is in the order of ms => machine interference problem l Operational => either thinking or typing l Hitting the return key => machine breaks down 3

Machine interference problem: assumptions l Problem (assumptions) l Operative l l Repair time l l Mean = 1/μ Repair queue l l Mean = 1/λ FIFO Finite population of customers 4

Machine interference problem: solution l Birth and death equations l What about P 0? 5

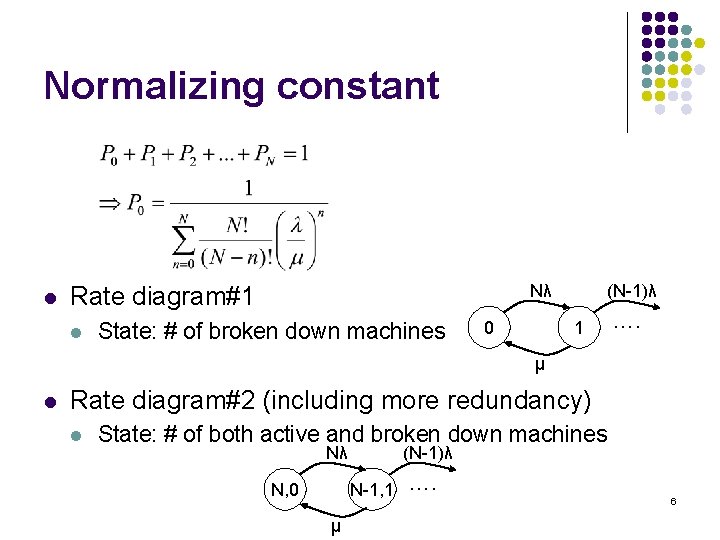
Normalizing constant l Nλ Rate diagram#1 l State: # of broken down machines 0 (N-1)λ 1 …. μ l Rate diagram#2 (including more redundancy) l State: # of both active and broken down machines Nλ N, 0 (N-1)λ N-1, 1 μ …. 6

Machine interference problem: performance measures l Mean repair’s man queue length l Mean # customers in the entire system l Mean waiting time (Little’s theorem) l What is the arrival rate to the repair’s man queue? W 7

Arrival rate to repair’s man queue and waiting time l Arrival rate to repair’s man queue l Mean waiting time in repair’s man queue l Mean waiting in the entire repair’s man system 8

Single machine: analysis l Cycle thru which goes a machine Operational Repair Wait l Mean cycle time l Rate at which a machine completes a cycle l Rate at which all machines complete their cycle 9

Production rate l # of repairs per unit time l Production rate l = rate at which you see machines l Going in front of you 10

Mean repair’s man queue length Lq 11

Normalized mean waiting time l W (mean waiting time) is given by l r = average operation time/average repair time l Normalized mean waiting time l W = 30 min, 1/μ=10 min => l normalized WT = 3 repair times 12

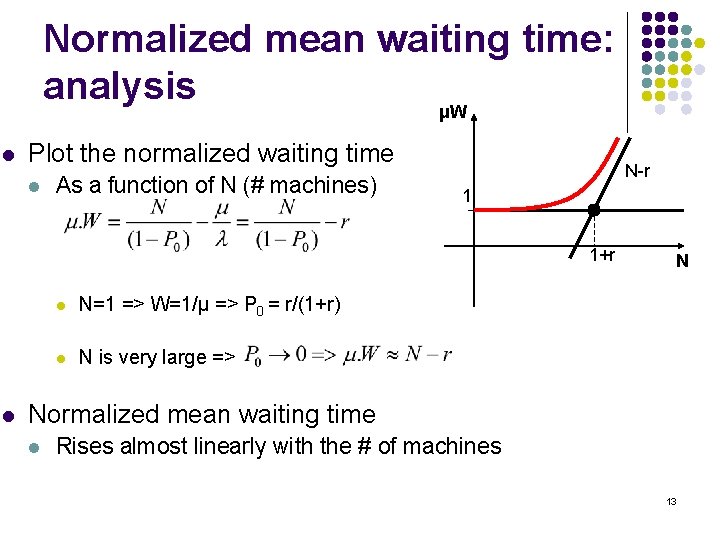
Normalized mean waiting time: analysis μW l Plot the normalized waiting time l As a function of N (# machines) N-r 1 1+r l l N=1 => W=1/μ => P 0 = r/(1+r) l N is very large => N Normalized mean waiting time l Rises almost linearly with the # of machines 13

Mean number of machines in the system L l Plot L as a function of N l N=1 => P 0 = r/(1+r) l l => L = 1/(1+r) L N is very large l L = N - r N-r 1/(1+r) N 14

Examples l Find the z-transform for l l Binomial, Geometric, and Poisson distributions And then calculate l The expected values, second moments, and variances l For these distributions 15

Z-transform: application in queuing systems l 16

Binomial distribution l 17

Geometric distribution l 18

Poisson distribution l 19

Problem I l 20

Problem I (cont’d) l Find the average number of customers in system 21

Problem II l In a networking conference l Each speaker has 15 min to give his talk l l Given that time to give a presentation is exponential l l Otherwise, he is rudely removed from podium With mean 10 min What is the probability a speaker will not finish his talk? l E[X] = 1/λ = 10 minutes => λ = 1/10 l Let T be the time required to give a presentation: a speaker will not manage § to finish his presentation if T exceeds 15 minutes. 22 l P(T>15) = e-1. 5

Problem III l Jobs arriving to a computer l require a CPU time l l exponentially distributed with mean 140 msec. The CPU scheduling algorithm is quantum-oriented l job not completing within 100 msec will go to back of queue l What is the probability that an arriving job will be forced to wait for a second quantum? l Of the 800 jobs coming per day, how many l Finish within the first quantum> 23

Problem IV l A taxi driver provides service in two zones of a city. l Customers picked up in zone A will have destinations l l Customers picked up in zone B will have destinations in l l zone A with probability 0. 3 or in zone B with probability 0. 7. The driver’s expected profit l l in zone A with probability 0. 6 or in zone B with probability 0. 4. for a trip entirely in zone A is 6$; for a trip in zone B is 8$; and for a trip involving both zones is 12$. Find the taxi driver’s average profit per trip. l Hint: condition on whether the trip is entirely in zone A, zone B, or 24 in both zones.

Problem V l Suppose a repairman has been assigned l l The responsibility of maintaining 3 machines. For each machine l The probability distribution of running time l l The repair time is also exponential l l Is exponential with a mean of 9 hours With a mean of 12 hrs Calculate the pdf and expected # of machines not running 25

Problem V (continued) l As a crude approximation l It could be assumed that the calling population is infinite l l => input process is Poisson with mean arrival rate of 3 / 9 hrs Compare the results of part 1 to those obtained from l M/M/1 model and an M/M/1/3 model l Which one is a better approximation? 26