Machine Coordinates Systems Lab 2 Absolute vs Incremental

Machine Coordinates Systems Lab 2: Absolute vs Incremental

Coordinate Worksheets l Provide to each student – – 3 Graph Sheets 1 Coordinate Worksheet

X and Y Co-ordinate Calculation Absolute and Incremental Co-ordinates l Absolute Co-ordinates – The G-code G 90 is used to select this type of programming. Before programming commences the points on the path to be machined are defined relative to the work piece datum: l l l G-code: text used for machining that defines machine movements Datum: a reference point from which ALL other points are referenced Examples of these co-ordinates are shown in the following graph The Z axis is the vertical axis and the datum used is normally the surface of the work, for the Boxford machines to recognize where the material first needs to be cut (machine slows feed rate to cut material). Z is positive when moving away from the surface and negative when moving towards or into the surface.

Absolute Co-ordinate System 1. Identify the co-ordinates of the origin in 3 dimensions 2. Assume the Datum is located at the origin 3. Create a table of X, Y, and Z co-ordinates of each letter labeled point; assume z=0 for all lettered positions

Absolute Co-ordinate Worksheet The Datum for X and Y are the origin (0, 0) The format for expressing X, Y, & Z is (x, y, z) so “Point A” = (5, 4, 0) when the datum is located at the origin Instructor: Go Back One Page for Students Datum A X 0 5 Y 0 4 Z 0 0 Point B C D E F G H

Answers to Absolute Co-ordinates The Datum for X, Y, and Z is the origin (0, 0, 0) So “Point B” = (10, 5, 0) relative to the Datum, “Point B” is NOT relative to “Point A” Point Datum A B C D E F G H X 0 5 10 -4 -9 -7 -4 7 5 Y 0 4 5 5 7 -3 -6 -5 -2 Z 0 0 0 0 0

Incremental Co-ordinates l Incremental Co-ordinates The G-code G 91 is used to select this type of programming. The points on the path to be machined are defined relative to the previous position. Identify the sequence of point coordinates needed to describe the points in the following table moving alphabetically, beginning at the Datum (0, 0, 0). The Z axis is again the vertical axis, and the points are defined relative to the previous position; positive when moving away from the surface and negative when moving towards or into the surface. For the problem, assume all Z co-ordinates equal zero.

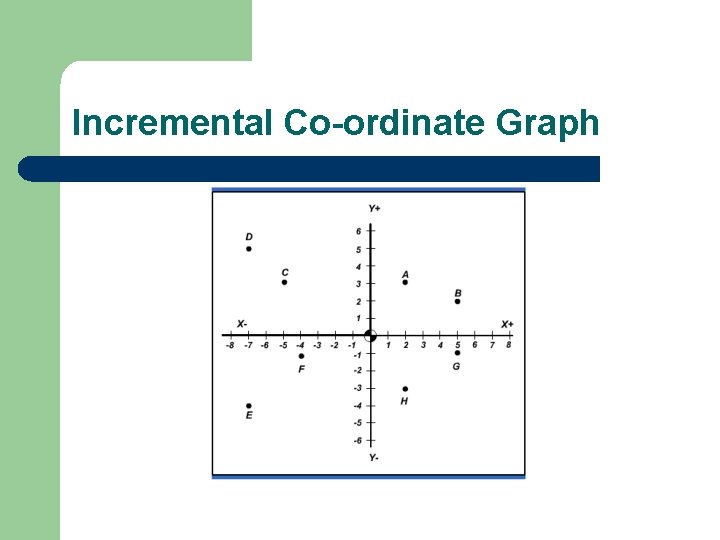
Incremental Co-ordinate Graph

Incremental Co-ordinate Worksheet The Datum for X, Y, and Z is the origin (0, 0, 0) so “Point A” = (2, 3, 0) in an incremental move from the datum Instructor: Go Back One Page for Students Datum A X 0 2 Y 0 3 Z 0 0 Point B C D E F G H

Answers to Incremental Co-ordinates The sequence specified moving “alphabetically”, therefore the following table represents incremental movements. Datum A B C D E F G H X 0 2 3 -10 -2 0 3 9 -3 Y 0 3 -1 1 2 -9 2 0 -3 Point Notice that the co-ordinate numbers associated with each lettered position would be completely different had the sequence been Datum, C, A, D, B, F, H, E, G So if one lettered position is in error, ALL subsequent positions will be in error

Incremental Co-ordinate Offset 1. If the Datum is moved to (0, 0, 1), and A is the first position to move to from the Datum, what happens to the incremental x and y values for position A? 2. If the Datum is moved from (0, 0, 0) to (0, 1, 0), what happens to the absolute x and y values for the actual desired position A? 3. If the Datum is moved to (1, 0, 0) from (0, 0, 0), what happens to the absolute positions of the lettered positions of the previous table? Instructor: Stop Here for Students

Answers 1. Only the z-axis of the Datum changed, therefore neither of the x or y values change. 2. X values are unchanged, however, subtract 1 from all y values. 3. The x, y, and z values are unaffected because the absolute values do not change. l As you can see, the concepts are simple, but one must be very careful when changing between absolute and incremental co-ordinate systems

Playing with G-codes l l G-codes are used to tell the CNC machines how to move from point to point Each line of G-code is numbered – – – l N 001 N 002 … The code following each line number is G-code – N 001 G 20 G 90 X 0. Y 0. Z 0. l l l Translation: move direct to Absolute coordinates (0, 0, 0) G 20 (direct to) and G 90 (absolute coordinates) A period is required within all G-code numbers

Playing with G-codes l l l IF G 90 says all following commands are in Absolute Coordinates AND G 91 says all following commands are in Incremental Coordinates THEN On a piece of graph paper mark a line between coordinates that show the toolpath that the following code describes – – use a heavy dot to mark each coordinate assume all transitions are in straight lines between coordinates

Playing with G-codes l l l l l N 001 G 20 G 90 X 0. Y 0. Z 0. N 002 G 20 G 90 X-1. Y-1. Z 0. N 003 G 20 G 91 X 0. Y 0. Z 0. N 004 G 20 G 91 X 2. Y 2. Z 0. N 005 G 20 G 91 X 0. Y-5. Z 0. N 006 G 20 G 91 X-5. Y 0. Z 0. N 007 G 20 G 90 X-4. Y-4. Z 0. N 008 G 20 G 91 X 4. Y 4. Z 0. N 009 G 20 G 90 X 0. Y 0. Z 0. Instructor: Stop Here for Students to make graph

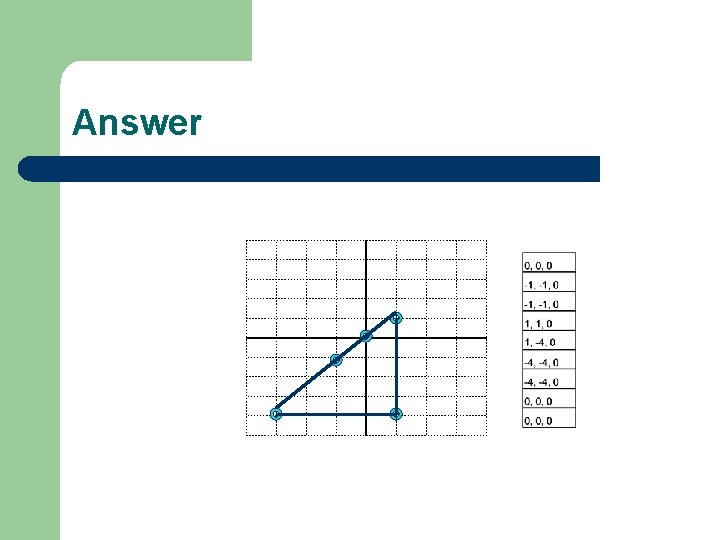
Answer

Including the Z-axis Adding the Z-axis complicates how we mentally move things in our minds However, if you haven’t noticed by now, incremental movements are very much related to addition and subtraction The following table provides a simple method of keeping track of coordinates when switching back and forth between coordinate systems; notice the simple addition and subtraction Remember: The table of the CNC machine is always in absolute coordinates

Including the Z-axis

Efficiency Means Money l In the G-code example presented, certain G-code statements had no effect upon the toolpath movement – l Basically, wasted statements Where time is money; what other manufacturing conditions can you imagine would cost money without providing significant useful result? – In corporate America it is estimated that at least 30% of all revenue is spent in the support of inefficient processes l l For example: parts being machined to tolerances tighter than necessary Think about this as you proceed through this lab series