Machine arithmetic and associated errors Introduction to error

Machine arithmetic and associated errors Introduction to error analysis Class II

Last time: • We discussed what the course is and is not • The place of computational science among other sciences • Class web site, computer setup, etc.

Today’s class. Background • Taylor Series: the workhorse of numerical methods. • F(x + h) =~ F(x) + h*F’(x) + h^2*F’’(x)/2! • • for x=0, sin(x+h) =~ h - (h^3)/3!, works very well for h << 1, OK for h < 1.

What is the common cause of these disasters/mishaps? Patriot Missile Failure, 1 st Gulf war, 1991 28 dead.

Numerical math != Math

Errors: Absolute and Relative Two numbers: X_exact and X_approx 1. 2. Absolute error of X_approx : |X_exact - X_approx | Relative error of X_approx (usually more important): (|X_exact - X_approx | / |X_exact|) x 100% Example: Suppose the exact number is X 1 = 0. 001, but we only have its approximation, X 2=0. 002. Then the relative error is: ((0. 002 - 0. 001)/0. 001)*100% = 100%. (Even though the absolute error is only 0. 001!)

A hands-on example: num_derivative. cc Let’s compute a numerical derivative of the function F(x) at x=1. 0 F(x) = exp(x) Use the definition of a derivative:

A hands-on example: numderivative. cc Let’s compute a numerical derivative of the function F(x) at x=1. 0 F(x) = exp(x) Use the definition of a derivative: F’(x) = d. F/dx = lim_{h-->0} (F(x+h)-F(x)) / h Where do the errors come from?

Defining functions in: numderivative. cc PRECISION f (PRECISION x ) { return exp(x); // function of interest } PRECISION exact_derivative (PRECISION x ) { return exp(x); // its exact analytical derivative } PRECISION num_derivative (PRECISION x, PRECISION h ) { return (f(x + h) - f(x))/h; // its numerical derivative }

Show the output from numderivative. cc

Where do the errors come from?

Two types of errors expected: 1. Truncation error. In our example - from using only the first two terms of Taylor series. (We will discuss this later) 2. Round-off error which leads to “loss of significance”.

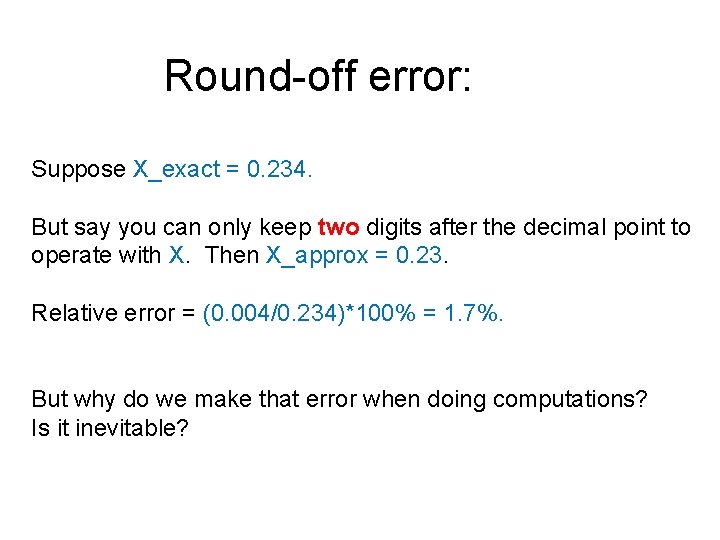
Round-off error: Suppose X_exact = 0. 234. But say you can only keep two digits after the decimal point to operate with X. Then X_approx = 0. 23. Relative error = (0. 004/0. 234)*100% = 1. 7%. But why do we make that error when doing computations? Is it inevitable?

The very basics of the floating point representation Real numbers in decimal form: 314. 159265 0. 00123654789 299792458. 00023 Normalized scientific notation (also called normalized floating-point representation): 0. 314159265 x 10^3 0. 123654789 x 10^(-2) 0. 29979245800023 x 10^9

Real numbers in decimal form: X=(+/-)0. d 1 d 2…. x 10^n where (d 1 != 0), n = integer. d 1, d 2 , … 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 (0 - not for d 1) Or X= (+/-) R x 10^n where 1/10 =< R < 1 R – normalized mantissa, n - exponent The floating-point representation of a real number in the binary system: X=(+/-)0. b 1 b 2 …. . x 2^k where b 1= 1, others 0 or 1, k = integer. Example: 1/10 = (0. 1100110011…. . ) x 2^(-3) (infinite series) Due to a finite length of mantissa in computers: MOST REAL NUMBERS CAN NOT BE REPRESENTED EXACTLY

Machine real number line has holes. -----|-------------------------- > 0 Example: Assume only 3 significant digits are allowed for a binary mantissa, that is possible numbers are X = (+/-)(0. b 1 b 2 b 3) x 2^k and k are allowed to be only k= +1, 0, or -1 What is smallest number above zero ?

Machine real number line has holes. -----|-------------------------- > 0 Example: Assume only 3 significant digits are allowed for a binary mantissa, that is possible numbers are X = (+/-)(0. b 1 b 2 b 3) x 2^k and k are allowed to be only k= +1, 0, or -1 What is smallest number above zero ? 0. 001 x 2^{-1} = 1/16 Largest = ?

Machine real number line has holes. -----|-------------------------- > 0 Example: Assume only 3 significant digits are allowed for a binary mantissa, that is possible numbers are X = (+/-)(0. b 1 b 2 b 3) x 2^k and k are allowed to be only k= +1, 0, or -1 What is smallest number above zero ? 0. 001 x 2^{-1} = 1/16 Largest = 0. 111 x 2^{1} = 7/4

Allowing only normalized floating-point numbers (b 1 = 1) we cannot represent 1/16 2/16 = 1/8 3/16 -|------------o--------o--------+-----0 1/4 | the first positive machine number = 0. 100 x 2^{-1} We have a relatively wide gap known as the hole at zero or underflow to zero. The numbers in this range are treated as 0. The number above 7/4 or below -7/4 would overflow to machine +/- infinity resulting in a fatal error.

How many bits of computer memory do we need to store the discussed above normalized floating-point numbers?

Realistic machine representation uses 32 bit or 4 bytes Float-point number = (+/-)q x 2^m. (IEEE-754 standard) (IEEE ("I triple E”) - The Institute of Electrical and Electronics Engineers) Single-precision floating-point numbers Mantissa q 23 bits Sign of q 1 bit Exponent integer |m| 8 bits Largest positive number ~ 2^128 ~ 3. 4 x 10^38 Smallest positive number ~ 10 ^-38 MACHINE EPSILON: smallest (+) e such that 1 + e > 1. e = 2^(-24) ~ 5. 96 x 10^(-8) ~ 10^(-7)

Errors in numerical approximations: Exact Solution -> Approximate Solution -> Numerical approximation No error Truncation Error Round-off Error Total error = truncation error + round-off error. Example worked out in class: numerical derivative, F’(x) ≈ [F(x + h) – F(x)] / h Total error ~ | F"(x)|max* h + |F(x)|max* emach / h. due to truncating the next term in Taylor expansion of F(x+h) [Decrease error with decreasing h] due to the round off error in the difference [F(x + h) – F(x)] [Increase error with further decrease of h ]

Errors in numerical approximations: Total error ~ | F"(x)|max* h + |F(x)|max* emach / h. Assuming that the function F(x) is not pathological, F” ~ F ~ 1 at x of interest, as in our example with F(x)=exp(x), minimum total error occurs at h ~ sqrt (emach ). For single precision, emach ~ 10^(-7) resulting in minimum total error of the F’(x) in our example at h ~ 10^(-3). For pathological functions, | F’’| or |F| may be very large, leading to large errors (and the minimum at a different spot).