Macchine di Turing 1 Il modello di base

Macchine di Turing (1) Il modello di base ha un controllo finito, un nastro di input diviso in celle e una testa di lettura che esamina una cella alla volta. a 1 a 2 . . . ai … an B B … Controllo finito Il numero di simboli di input è finito. L’input è nelle n celle più a sinistra (n finito). Nelle celle rimanenti c’è un simbolo speciale blank che non è un simbolo di input. In una mossa in funzione del simbolo esaminato dalla testa di lettura e dallo stato del controllo la macchina può: 1. Cambiare stato 2. Stampare un simbolo nella cella letta sostituendo il simbolo presente 3. Muovere la testa di lettura di una posizione a destra o a sinistra

Macchine di Turing (2) Una macchina di Turing (TM) è M = (Q, S, D, d, q 0, B, F) dove: Q insieme finito degli stati, d : Q G {L, R}, G insieme dei simboli di nastro, q 0 stato di partenza, B blank, F Q insieme degli stati finali, S G-B insieme dei simboli di input Una descrizione istantanea (ID) di una TM M è a 1 qa 2 dove q stato corrente, a 1 a 2 stringa in G * contenuto del nastro (da sinistra e fino a un blank a destra). La testa di lettura sta leggendo il simbolo più a sinistra di a 2 oppure blank se a 2 = e. Sia la ID x 1 x 2. . . xi-1 q xi. . . xn. Se d(q, xi) = (p, y, L) per i>1 allora x 1 x 2. . . xi-1 q xi. . . xn |-M x 1 x 2. . . xi-2 p xi-1 Y xi+1. . . xn Se d(q, xi) = (p, y, R) allora x 1 x 2. . . xi-1 q xi. . . xn |-M x 1 x 2. . . xi-1 Y p xi+1. . . xn.

Macchine di Turing (3) Una TM M = (Q, S, G, d, q 0, B, F) accetta il linguaggio {w | w in S* e q 0 w |-M* a 1 p a 2 per p F, a 1, a 2 G*} Il linguaggio accettato da una TM è detto ricorsivamente enumerabile (r. e. ). Esempio. Una TM che accetta L = {0 n 1 n| n >= 1}, Idea: M sostituisce lo 0 più a sinistra con X, poi muove a destra fino all’ 1 più a sinistra e lo sostituisce con Y, muove a sinistra per trovare la X più a destra e muove a destra per trovare uno 0 e ripete il ciclo.

Macchine di Turing (4) Allora M = ({q 0, q 1, q 2, q 3, q 4}, {0, 1, X, Y, B}, d, q 0, B, { q 4}) dove d è data dalla tabella seguente: q 0 q 1 q 2 q 3 q 4 0 (q 1, X, R) (q 1, 0, R) (q 2, 0, L) 1 (q 2, Y, L) (q 0, X, R) - X - - Y (q 3, Y, R) (q 1, Y, R) (q 2, Y, L) (q 3, Y, R) - B - (q 4, B, R) - Una computazione possibile è: q 0 0 0 1 1 |- X q 1 0 1 1 |- X 0 q 1 1 1 |- X q 2 0 Y 1 |- q 2 X 0 Y 1 |- X q 0 0 Y 1 |- X X q 1 Y 1 |- X X Yq 1 1 |- X X q 2 YY |- X q 2 XYY |- XX q 0 YY |- XXYq 3 Y |- XXYY q 3 |- XXYY q 4

Macchine di Turing (5) Una macchina di Turing con un nastro infinito a due vie assume che ci sia un’infinità di blank a sinistra e a destra della porzione scritta. La relazione |-M differisce da quella della TM a una via perché se d(q, X) = (p, Y, L) allora q X a |-M p BY a (mentre nel modello a una via non si può fare nessuna mossa) e se d(q, X) = (p, B, R) allora q X a |-M p a (non segna un blank a sinistra perché ce ne possono essere infiniti). Teorema. L è riconosciuto da una macchina di Turing con nastro due vie se e solo se è riconosciuto da una macchina di Turing con nastro a una via

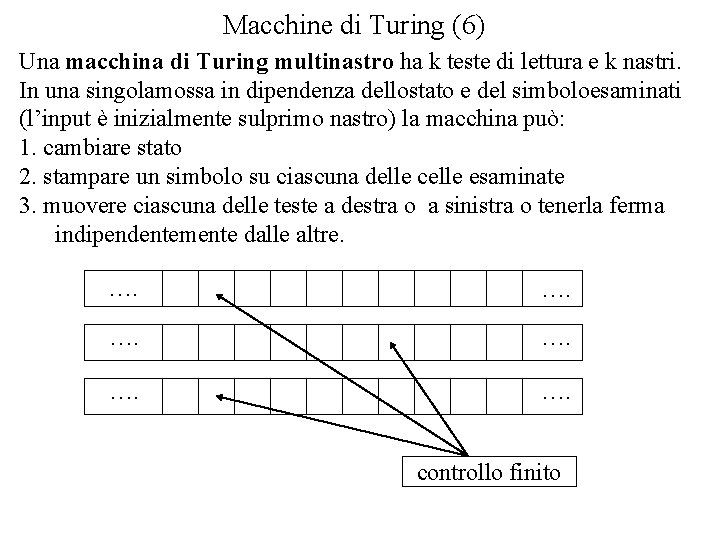
Macchine di Turing (6) Una macchina di Turing multinastro ha k teste di lettura e k nastri. In una singolamossa in dipendenza dellostato e del simboloesaminati (l’input è inizialmente sulprimo nastro) la macchina può: 1. cambiare stato 2. stampare un simbolo su ciascuna delle celle esaminate 3. muovere ciascuna delle teste a destra o a sinistra o tenerla ferma indipendentemente dalle altre. …. …. …. controllo finito

Macchine di Turing (7) Teorema. Se un linguaggio L è accettato da una macchina di Turing multinastro è accettato da una macchina di Turing a un solo nastro. Esempio. L = {ww. R | w in (0+1)*} è accettato in tempo proporzionale alla lunghezza dell’input da una macchina di Turing a due nastri. L’input è copiato sul secondo nastro e le due teste sono mosse in direzioni opposte confrontando i simboli letti da ciascuna.

Macchine di Turing (8) Una TM non deterministica può avere piú di una scelta in uno stato per un simbolo letto. Teorema. Se un linguaggio L è accettato da una TM non deterministica M 1 allora è accettato da una TM deterministica M 2. Prova. La macchina M 2 ha tre nastri. Il primo contiene l’input. Per ogni stato e simbolo letto c’è un numero finito di scelte per la mossa Successiva e una sequenza finita di scelte può essere rappresentata da una sequenza di cifre 1, 2, … , r. La macchina M 2 genera sequenze in modo sistematico sul secondo nastro, copia l’input sul terzo nastro e simula M 1 sul terzo nastro secondo le mosse indicate sul secondo nastro. Se c’è una sequenza che porta all’accettazione dell’input prima o poi compare sul secondo nastro e l’input è accettato. Teorema (della fermata). Data una TM M e un input w è indecidibile se M accetta w.

Decidibilità (1) Un linguaggio è ricorsivamente enumerabile (r. e. ) se le parole del linguaggio possono essere enumerate. Se questo avviene in modo che le parole si seguano in ordine crescente il linguaggio è ricorsivo. Istanze di problemi possono essere codificate come parole di un linguaggio. Esempio. Il problema se una TM accetta la stringa vuota è codificato come il linguaggio di tutte le codifiche di TM che accettano la parola vuota. Poiché il linguaggio è ricorsivamente enumerabile ma non ricorsivo, il problema se una TM data accetta la parola vuota è indecidibile.

Decidibilità (2) Teorema. Il complemento di un linguaggio ricorsivo è ricorsivo. Teorema. L’unione di due linguaggi r. e. è r. e. . L’unione di due linguaggi ricorsivi è ricorsiva. Teorema. Se un linguaggio L e il suo complemento sono r. e. allora L è ricorsivo. Teorema. Il linguaggio universale Lu= {<M, w> | una TM M accetta la stringa w} è r. e. ma non ricorsivo. Nota. Lu è detto universale perché la domanda se una particolare stringa w’ è accettata da una macchina di Turing M’ è equivalente alla domanda se <M’, w’> è in Lu. Il complemento di non è neanche r. e. .

Decidibilità (3) Teorema. Sono indecidibili le seguenti proprietà degli insiemi r. e. : vuotezza, finitezza, regolarità, noncontestualità. Corollario. Per CFG arbitrarie G 1 e G 2 è indecidibile se L(G 1) L(G 2) è vuoto. Prova. Si dimostra che l’insieme delle computazioni valide di una TM è l’intersezione di due linguaggi noncontestuali L 1 e L 2 e che grammatiche L 1 e L 2 si possono costruire effettivamente da TM. Se allora decidessimo la vuotezza decideremmo la vuotezza degli insiemi r. e. .

Decidibilità (4) Teorema. Per grammatiche noncontestuali arbitrarie sono indecidibili i problemi seguenti: 1. L(G) = S* 2. L(G 1) = L(G 2) 3. L(G 1) = R 4. R L(G 1) Prova. 1. Data una TM M l’insieme delle computazioni non valide è un CFL. Allora dalla TM possiamo costruire una CFG G tale che L(G) = S* se e solo se L(M) = . Allora se decidessimo L(G) = S* decideremmo la vuotazza dei linguaggi r. e. . 2. -3. -4. si riconducono all’indecidibilità di L(G) = S*.

Gerarchia di Chomsky (1) Una CFG è lineare destra se tutte le produzioni sono della forma A w. B oppure A w con A, B nonterminali e w stringa di terminali (eventualmente vuota). Analogamente si definisce una CFG lineare sinistra. Grammatiche lineari destre e sinistre sono dette regolari. Teorema. Se L ha una grammatica regolare è un linguaggio regolare. Prova. Sia L= L(G) per una grammatica lineare destra G = (V, T, P, S). Costruiamo un NFA con e-transizioni M = (Q, T, d, [S], {[e]}) dove: - Q è l’insieme degli stati [a] dove a è un suffisso di lato destro di produzione in P - d([A], e) = {[a] | A a in P} - se a T*V allora d([aa], a) = {[a]}. Per induzione sulla lunghezza delle sequenze di derivazione si vede che d([S], w) contiene a se e solo se S Þ* x. A Þ xya dove A ya in P e xy=w oppure a = S e w = e. Poiché [e] è l’unico stato finale M accetta w se e solo se S Þ* x. A Þ w.

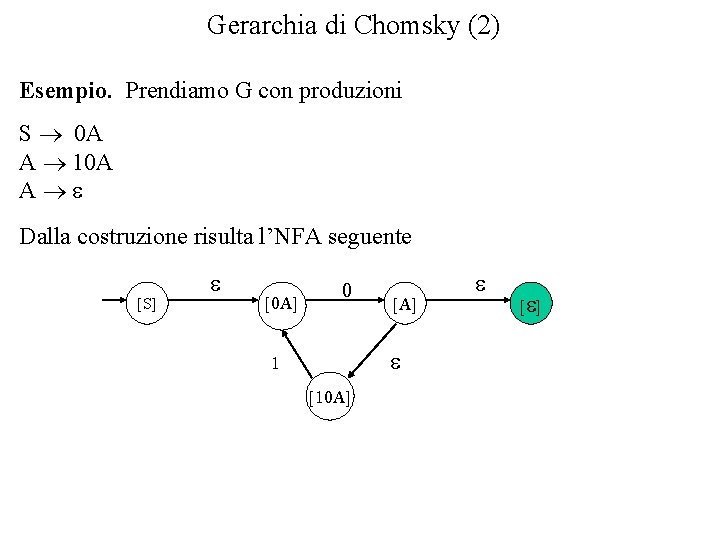
Gerarchia di Chomsky (2) Esempio. Prendiamo G con produzioni S 0 A A 10 A A e Dalla costruzione risulta l’NFA seguente [S] e [0 A] 0 [A] e 1 [10 A] e [e ]

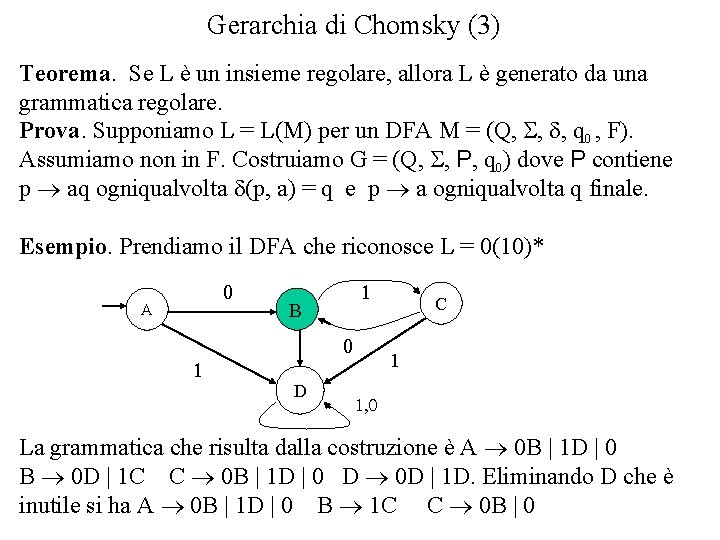
Gerarchia di Chomsky (3) Teorema. Se L è un insieme regolare, allora L è generato da una grammatica regolare. Prova. Supponiamo L = L(M) per un DFA M = (Q, S, d, q 0 , F). Assumiamo non in F. Costruiamo G = (Q, S, P, q 0) dove P contiene p aq ogniqualvolta d(p, a) = q e p a ogniqualvolta q finale. Esempio. Prendiamo il DFA che riconosce L = 0(10)* 0 A 1 1 B 0 D C 1 1, 0 La grammatica che risulta dalla costruzione è A 0 B | 1 D | 0 B 0 D | 1 C C 0 B | 1 D | 0 D 0 D | 1 D. Eliminando D che è inutile si ha A 0 B | 1 D | 0 B 1 C C 0 B | 0

Gerarchia di Chomsky (4) Una grammatica è non ristretta o di tipo 0 se è G = (V, T, P, S) dove le produzioni sono della forma a b con stringhe arbitrarie di simboli e a non è e. Esempio. G = ({S, A, B, C, D, E}, {a}, P, S) dove P è: S ACa. B Ca aa. C CB DB CB E a. D Da AD AC a. E Ea AE e L(G)= {ai | i potenza positiva di 2}. Teorema. Se L è L(G) per una grammatica non ristretta allora è un linguaggio r. e. . Prova. Si costruisce una macchina di Turing a due nastri non deterministica che riconosce L.

Gerarchia di Chomsky (5) Una grammatica non ristretta con produzioni a b con la condizione |a| £ |b| è chiamata grammatica contestuale (CSG) e il linguaggio che genera è chiamato linguaggio contestuale (CSL). Una formanormale per le grammatiche contestuali ha regole della forma a 1 Aa 2 a 1 ba 2 con b non e. Un LBA è una macchina di Turing ristretta alla porzione di nastro su cui è l’input piú due celle che contengono i marcatori terminali # e $. Un LBA è M = (Q, S, G, d, &, $, F). Il linguaggio accettato da M è {w | w in (S-{#, $})* e q 0#w$ |-M* a q b per q F}. Teorema. Se L è un CSL allora L è accettato da un LBA.

Gerarchia di Chomsky (6) Esempio. L = {aibici | i 1} è generato dalla CSG G = ({S, S’, S”’} {a, b, c}, P, S) con P S abc. S’ S’c b. S’ S’b a. S’ aa. S” S”b bb. S’” S”’b b. S’” S”’c cc. S’ S”’c cc Teorema. Ogni CSL è ricorsivo. Prova. Data una CSG G = (V, T, P, S) e una parola w in S* di lunghezza n costruiamo un grafo i cui vertici sono le parole in (V T)* di lunghezza n o meno. Poniamo un arco da a a b se a Þ b. Allora w è in L(G) se e solo se c’è un cammino dal vertice per S al vertice per w. Per rispondere a questo usiamo un algoritmo di ricerca di cammini.

Gerarchia di Chomsky (7) Teorema. Esiste un linguaggio ricorsivo che non è un CSL. Teorema. I CSL sono chiusi per - unione - concatenazione - intersezione - sostituzione - omomorfismo inverso - chiusura positiva. Teorema. Per i CSL sono indecidibili le seguenti proprietà: - il CSL è vuoto - il CSL è uguale a S+.

Gerarchia di Chomsky (8) Teorema (teorema della gerarchia). 1. Gli insiemi regolari sono contenuti propriamente nei CFL. 2. I CFL non contenenti la stringa vuota sono contenuti propriamente nei CSL. 3. I CSL sono contenuti propriamente nei linguaggi r. e. . Prova. 1. Dal fatto che ogni grammatica regolare è una CFG e che {anbn | n 1} non è regolare per il pumping lemma. 2. Dal fatto che ogni CFG in Chomsky Normal Form è una CSG e e che {anbncn | n 1} è un CSL che non è un CFL per il pumping lemma. 3. Segue dal fatto che una CSG è una grammatica ristretta e che i CSL sono ricorsivi.