Lyt og lr Vibration Theory Overview Severity levels

Lyt og lær Vibration Theory

Overview • • Severity levels Filters Detectors (RMS, peak-peak, Crest factor) Frequency analysis Displacement, Velocity Acceleration Resonances Different signal types (in time domain) – Harmonics – Pulses – Random noise

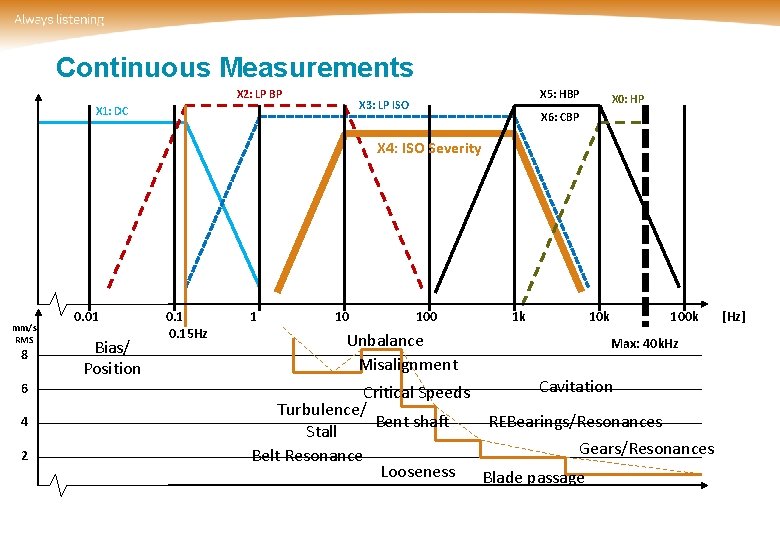
Continuous Measurements X 2: LP BP X 5: HBP X 3: LP ISO X 1: DC X 0: HP X 6: CBP X 4: ISO Severity mm/s RMS 8 6 4 2 0. 01 Bias/ Position 0. 15 Hz 1 10 100 Unbalance Misalignment 1 k 100 k Max: 40 k. Hz Cavitation Critical Speeds Turbulence/ Bent shaft REBearings/Resonances Stall Gears/Resonances Belt Resonance Looseness Blade passage [Hz]

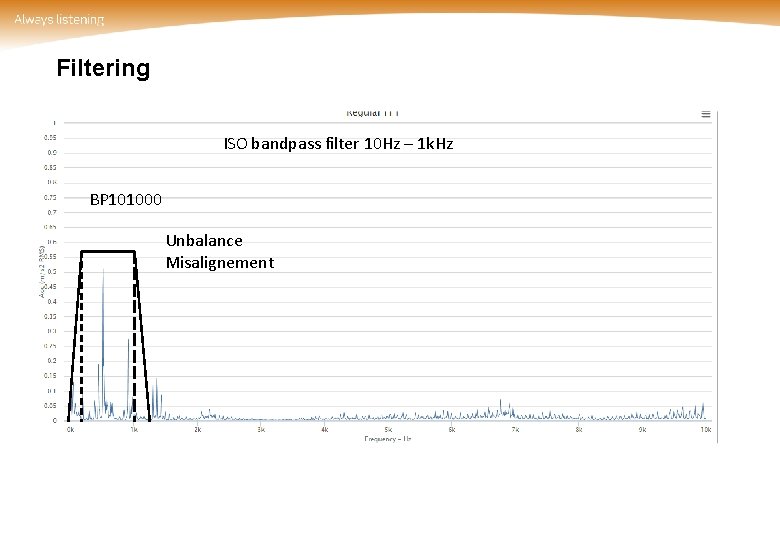
Filtering ISO bandpass filter 10 Hz – 1 k. Hz BP 101000 Unbalance Misalignement

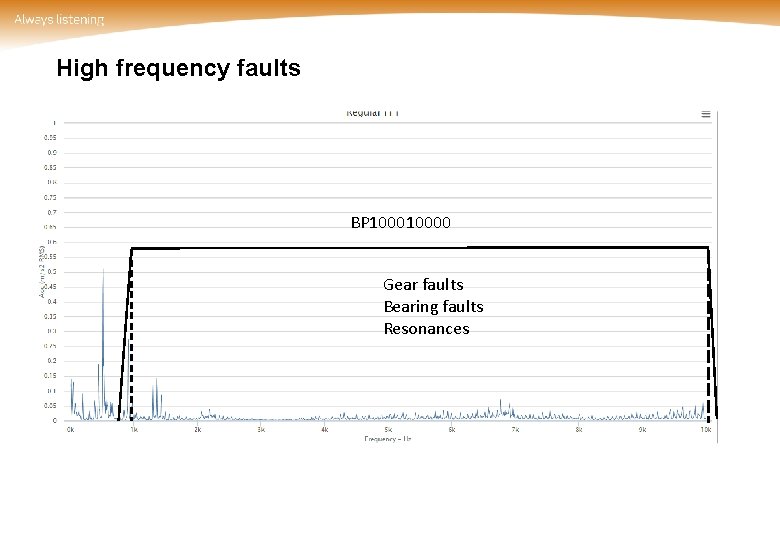
High frequency faults BP 10000 Gear faults Bearing faults Resonances

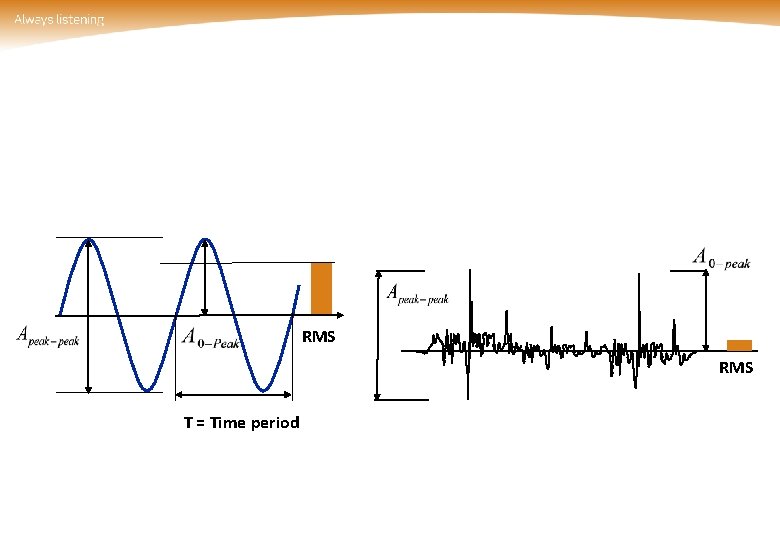
RMS T = Time period

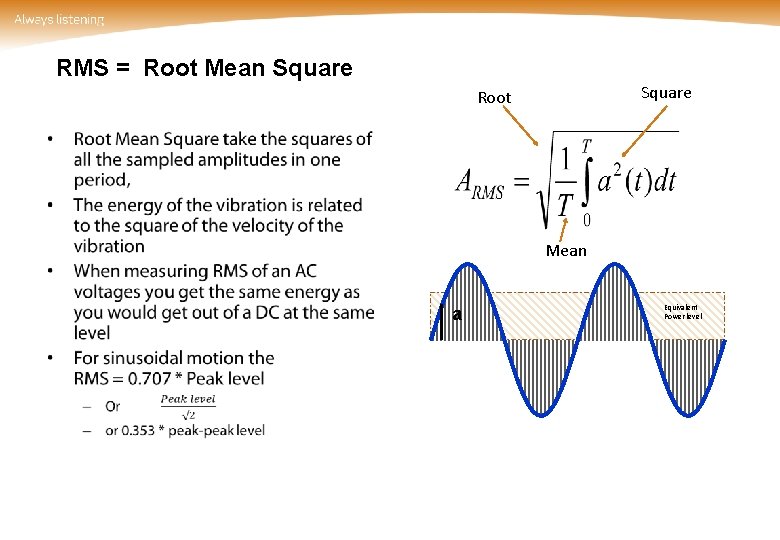
RMS = Root Mean Square Root • Mean a Equivalent Power level

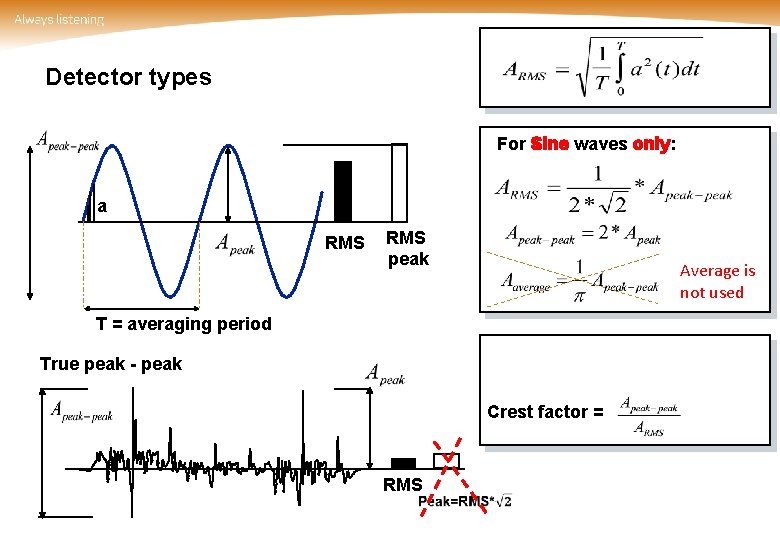
Detector types For Sine waves only: a RMS peak Average is not used T = averaging period True peak - peak Crest factor = RMS

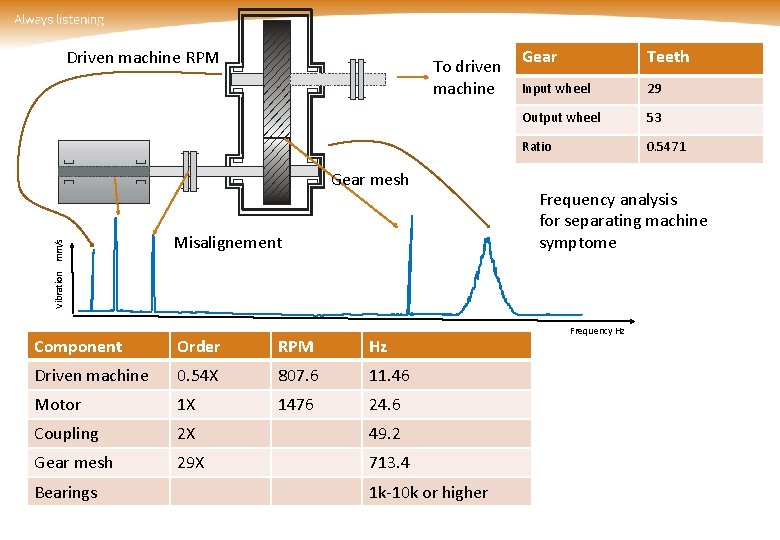
Driven machine RPM To driven machine Vibration mm/s Gear mesh Misalignement Component Order RPM Hz Driven machine 0. 54 X 807. 6 11. 46 Motor 1 X 1476 24. 6 Coupling 2 X 49. 2 Gear mesh 29 X 713. 4 Bearings 1 k-10 k or higher Gear Teeth Input wheel 29 Output wheel 53 Ratio 0. 5471 Frequency analysis for separating machine symptome Frequency Hz

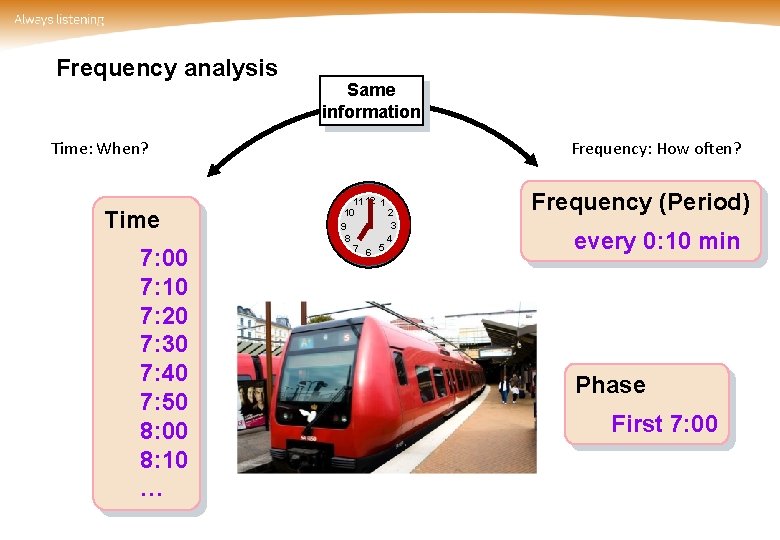
Frequency analysis Same information Time: When? Time 7: 00 7: 10 7: 20 7: 30 7: 40 7: 50 8: 00 8: 10 … Frequency: How often? 11 12 1 10 2 3 9 4 8 7 6 5 Frequency (Period) every 0: 10 min Phase First 7: 00

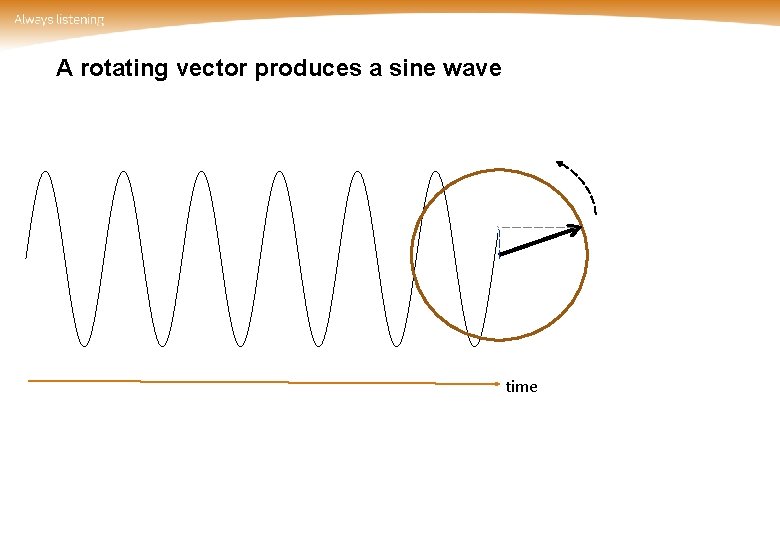
A rotating vector produces a sine wave time

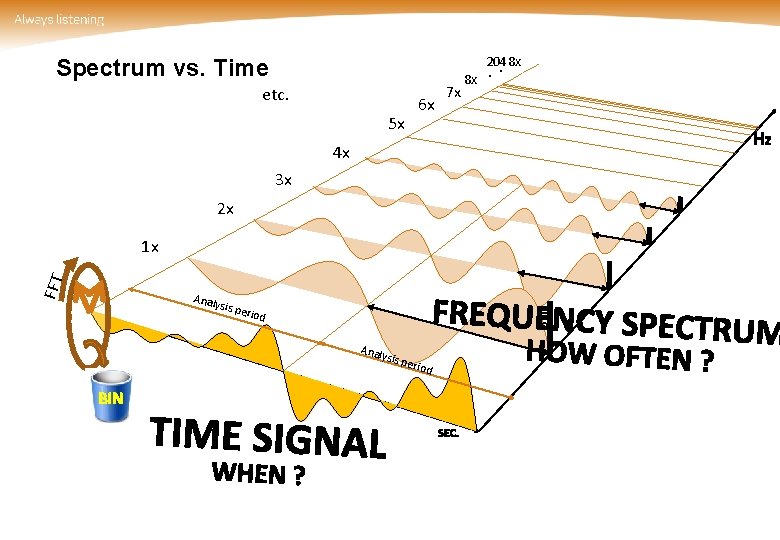
Spectrum vs. Time etc. 5 x 6 x 7 x 8 x 2048 x. . 4 x 3 x 2 x FFT 1 x Analy sis pe Bin riod Anal ys is pe riod BIN

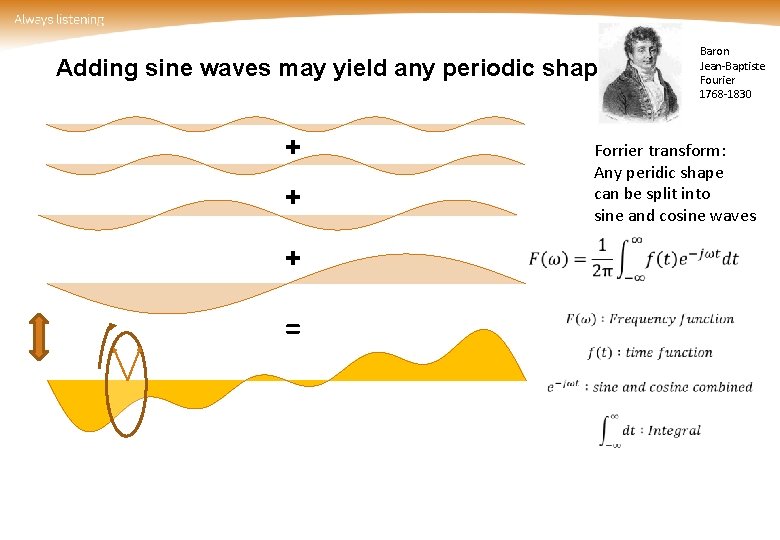
Adding sine waves may yield any periodic shape + Forrier transform: Any peridic shape can be split into sine and cosine waves + + = Baron Jean-Baptiste Fourier 1768 -1830

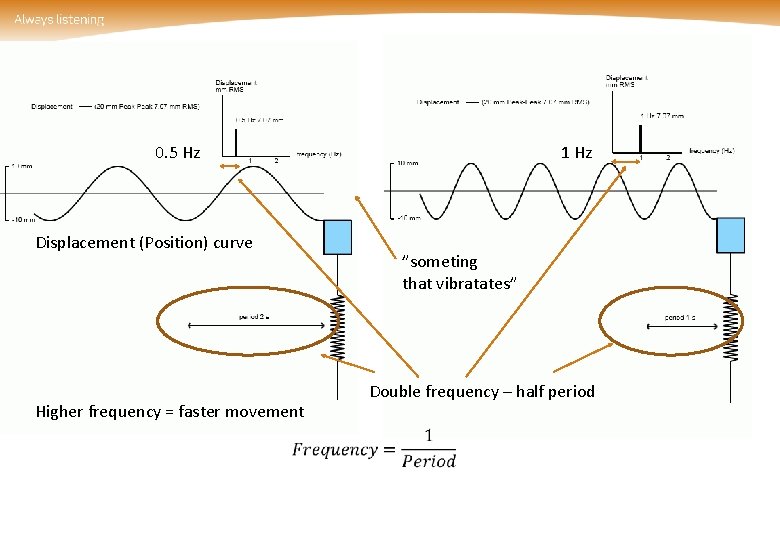
0. 5 Hz Displacement (Position) curve Higher frequency = faster movement 1 Hz ”someting that vibratates” Double frequency – half period

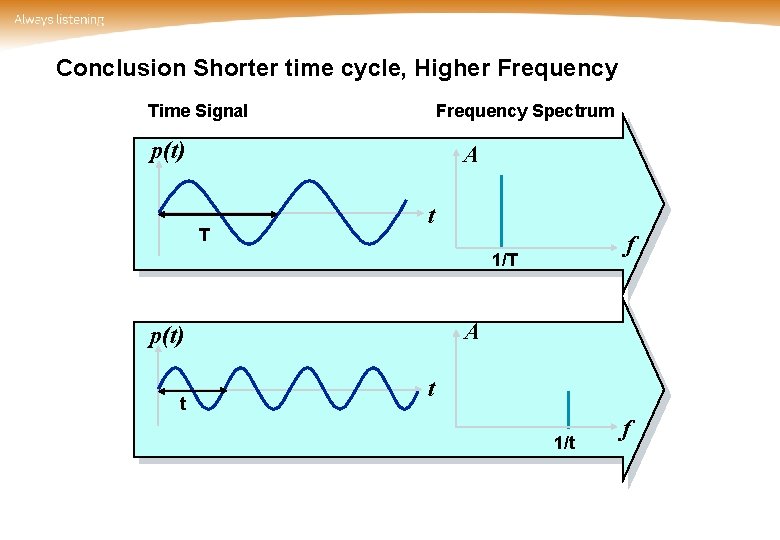
Conclusion Shorter time cycle, Higher Frequency Time Signal Frequency Spectrum p(t) A T t f 1/T A p(t) t t 1/t f

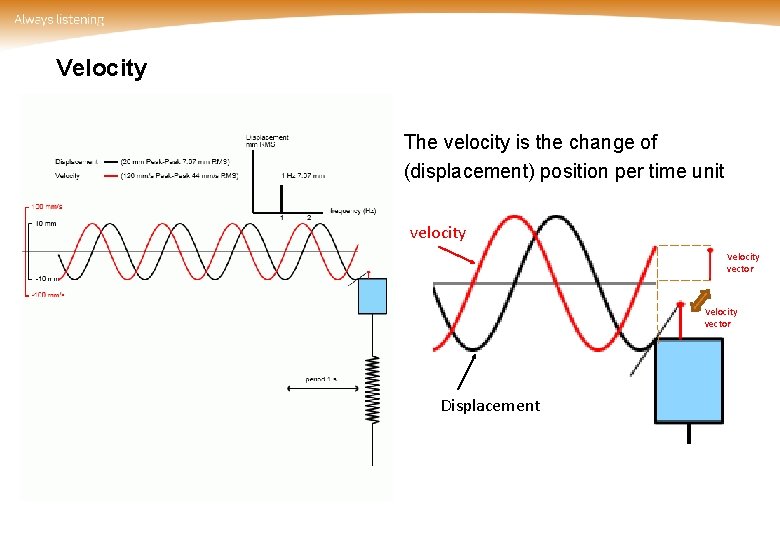
Velocity The velocity is the change of (displacement) position per time unit velocity Velocity vector Displacement

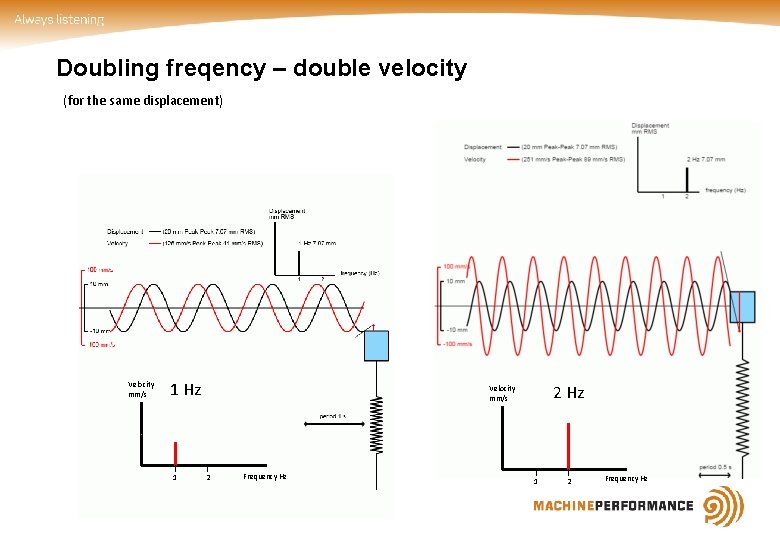
Doubling freqency – double velocity (for the same displacement) Velocity mm/s 1 Hz 1 2 Hz Velocity mm/s 2 Frequency Hz 1 2 Frequency Hz

Acceleration = Change of velocity with time Constant Acceleration (of ball only) Constant speed (of ball and car)

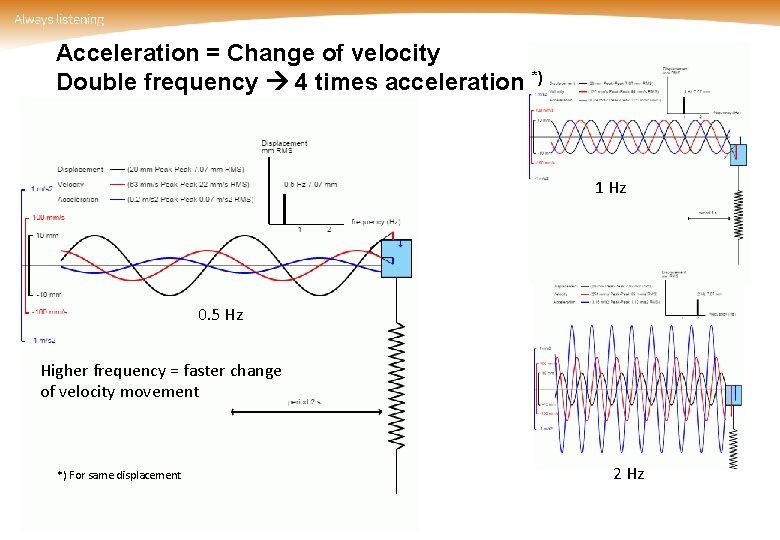
Acceleration = Change of velocity Double frequency 4 times acceleration *) 1 Hz 0. 5 Hz Higher frequency = faster change of velocity movement *) For same displacement 2 Hz

Sensors measure Acceleration, Velocity or Displacement sensor Velocity sensor ÷ The design contain moving parts ÷ Limited frequency range + Accelerometer Most versatile for vibration meaurements The acceleration signal may be integrated to velocity and displacement Good signal Measure the distance from bearing to shaft Used in journal bearing machines and for tacho application

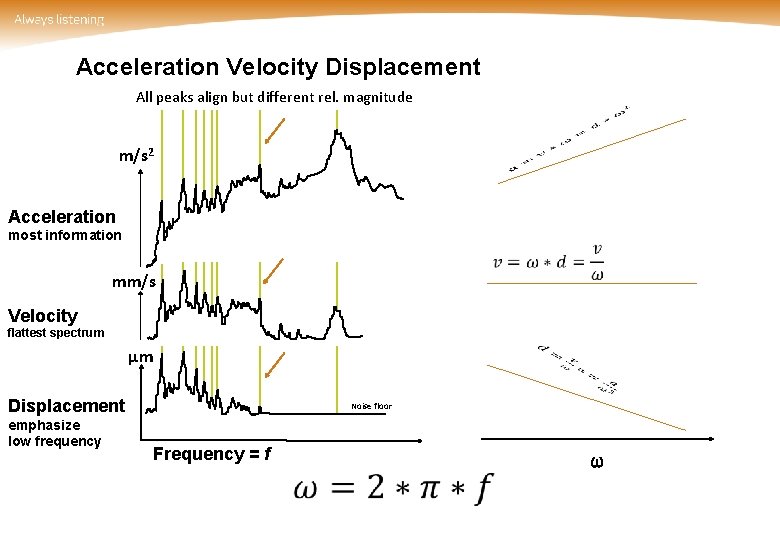
Acceleration Velocity Displacement All peaks align but different rel. magnitude m/s 2 Acceleration most information mm/s Velocity flattest spectrum µm Displacement emphasize low frequency Noise floor Frequency = f ω

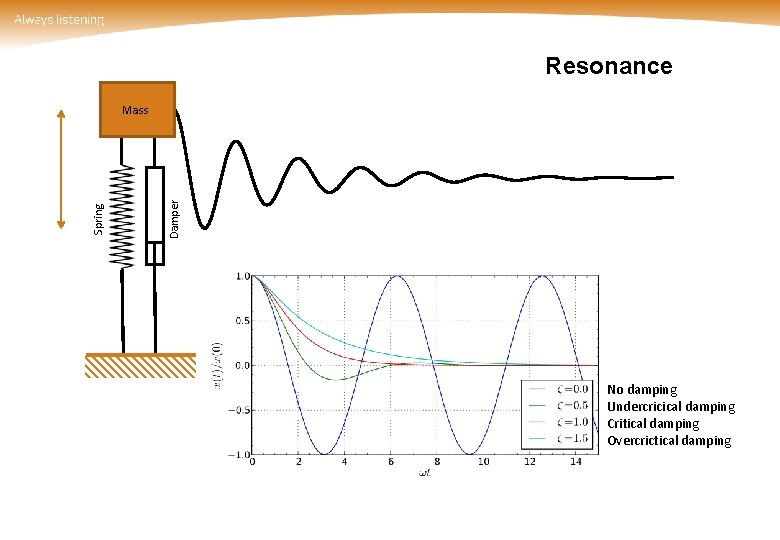
Resonance Damper Spring Mass No damping Undercricical damping Critical damping Overcrictical damping

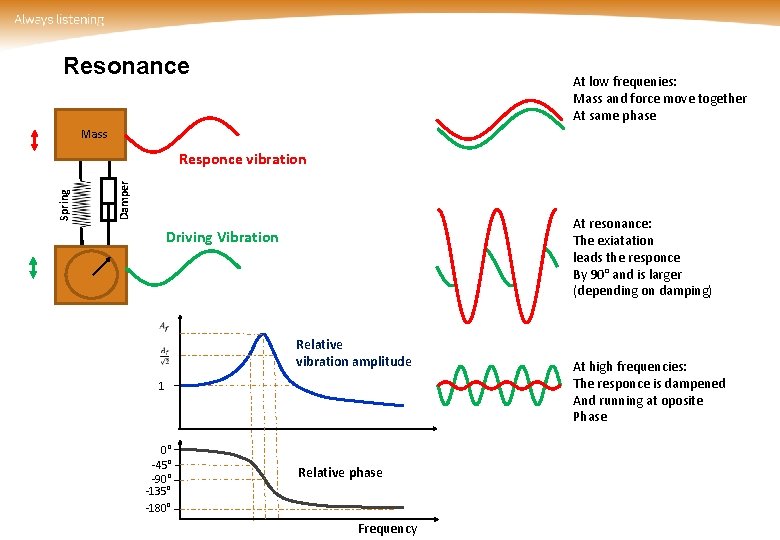
Resonance At low frequenies: Mass and force move together At same phase Mass Damper Spring Responce vibration At resonance: The exiatation leads the responce By 90° and is larger (depending on damping) Driving Vibration Relative vibration amplitude 1 0° -45° -90° -135° -180° Relative phase Frequency At high frequencies: The responce is dampened And running at oposite Phase

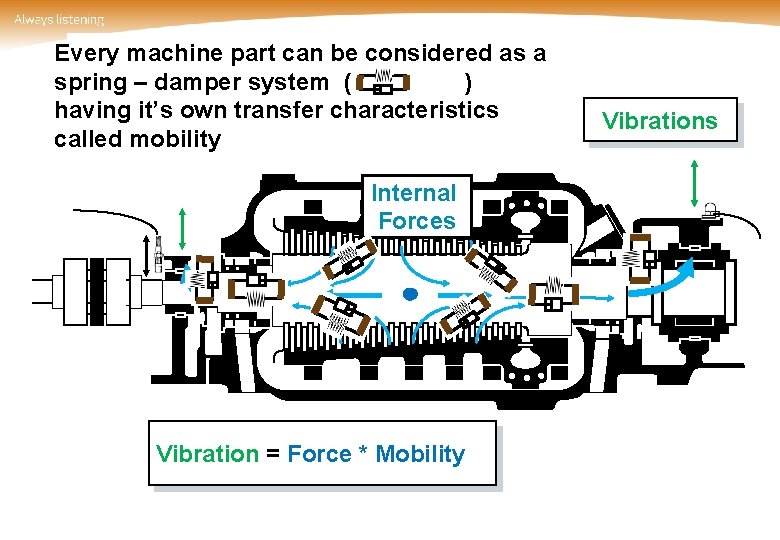
Every machine part can be considered as a spring – damper system ( ) having it’s own transfer characteristics called mobility Internal Forces Vibration = Force * Mobility Vibrations

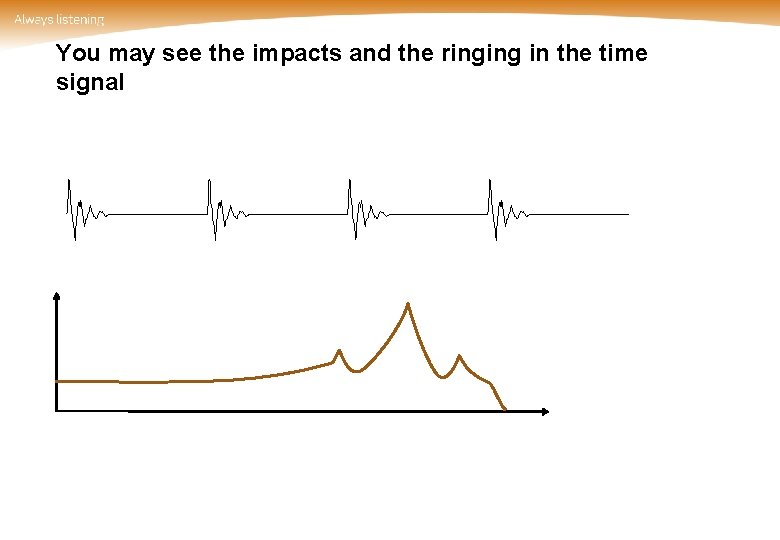
You may see the impacts and the ringing in the time signal

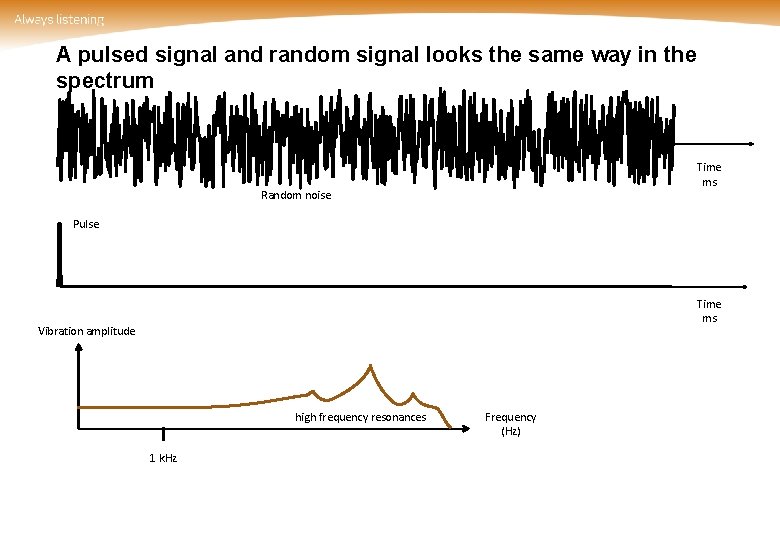
A pulsed signal and random signal looks the same way in the spectrum Time ms Random noise Pulse Time ms Vibration amplitude high frequency resonances 1 k. Hz Frequency (Hz)

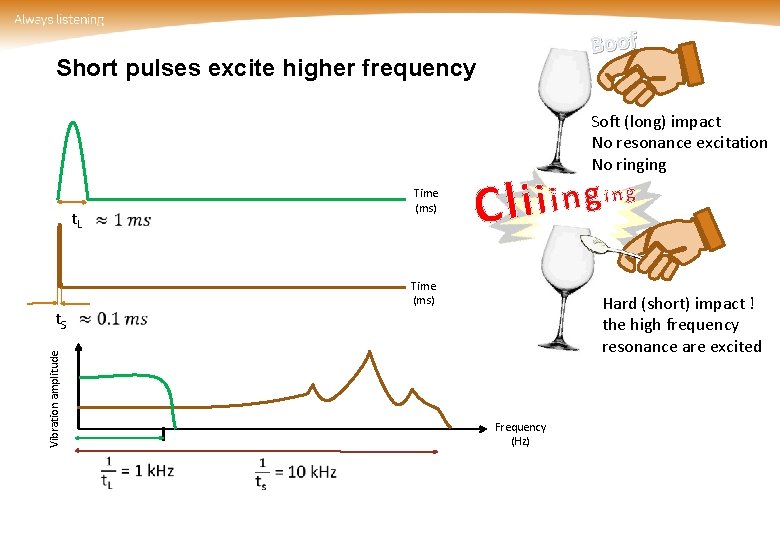
Boof Short pulses excite higher frequency Soft (long) impact No resonance excitation No ringing Time (ms) t. L ing g n i Clii Time (ms) Vibration amplitude t. S Hard (short) impact ! the high frequency resonance are excited Frequency (Hz)

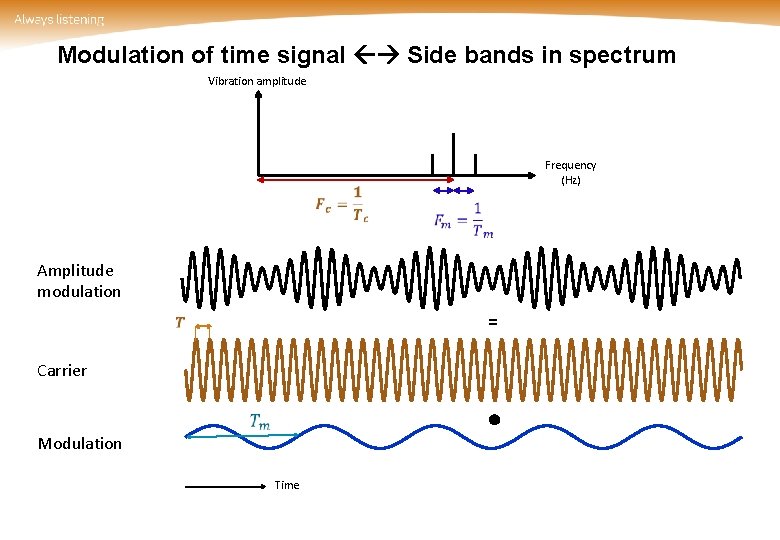
Modulation of time signal Side bands in spectrum Vibration amplitude Frequency (Hz) Amplitude modulation = Carrier Modulation Time

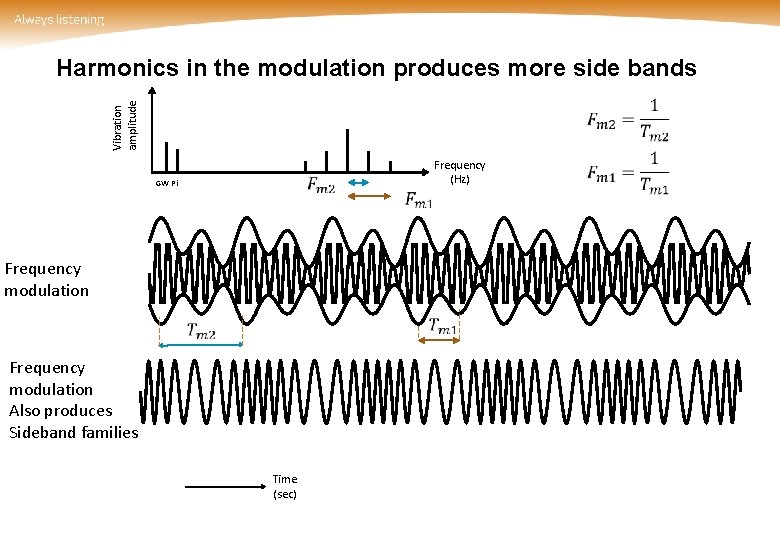
Harmonics in the modulation produces more side bands Vibration amplitude GW Pi Frequency (Hz) Frequency modulation Also produces Sideband families Time (sec)

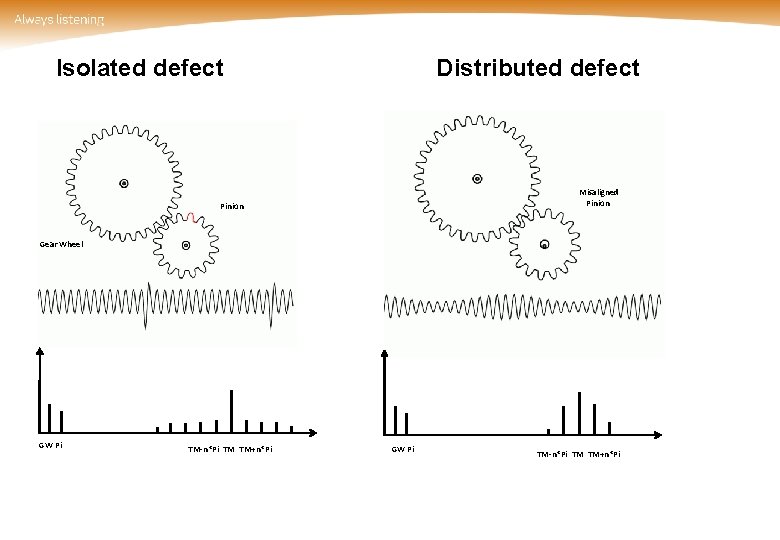
Isolated defect Distributed defect Misaligned Pinion Gear Wheel GW Pi TM-n*Pi TM TM+n*Pi

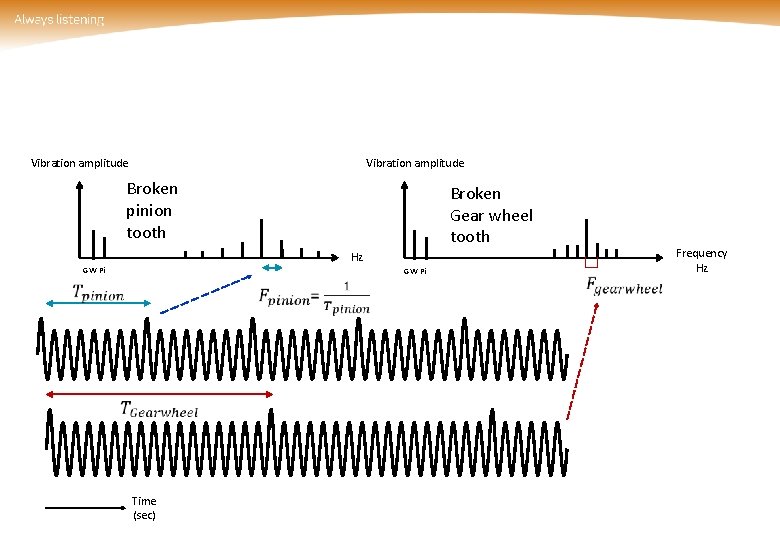
Vibration amplitude Broken pinion tooth Broken Gear wheel tooth Hz GW Pi Time (sec) Frequency Hz

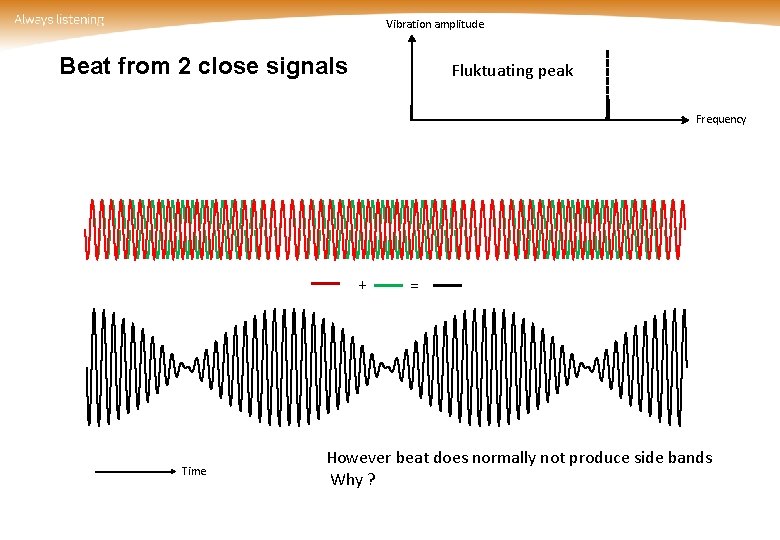
Vibration amplitude Beat from 2 close signals Fluktuating peak Frequency + Time = However beat does normally not produce side bands Why ?

Bearings produces unique bearing frequencies • Outer race faults – 1 – 6 month from detection to critical • Inner race faults – 1 – 4 weeks from detection to critical • Ball faults – 1 hour – 1 day from detection to critical