LUKUALUEET Luonnolliset luvut N 0 1 2 3











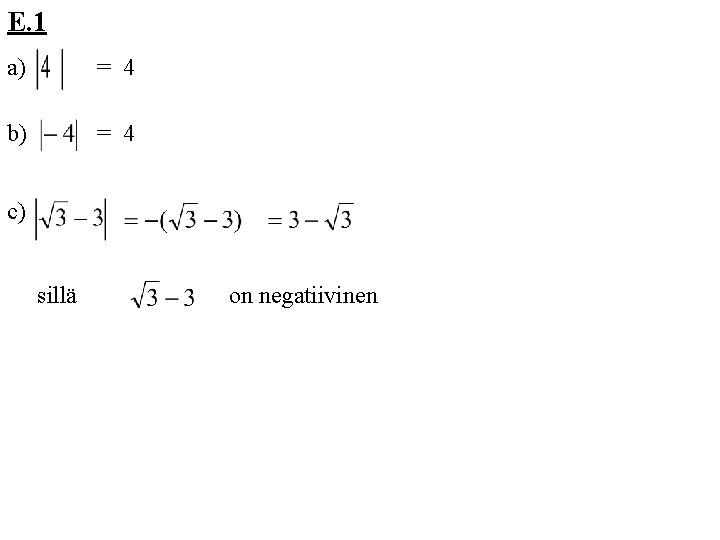



























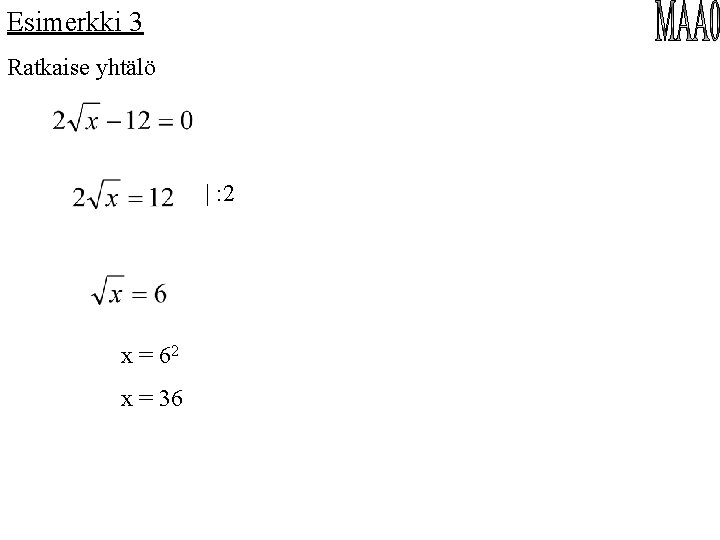


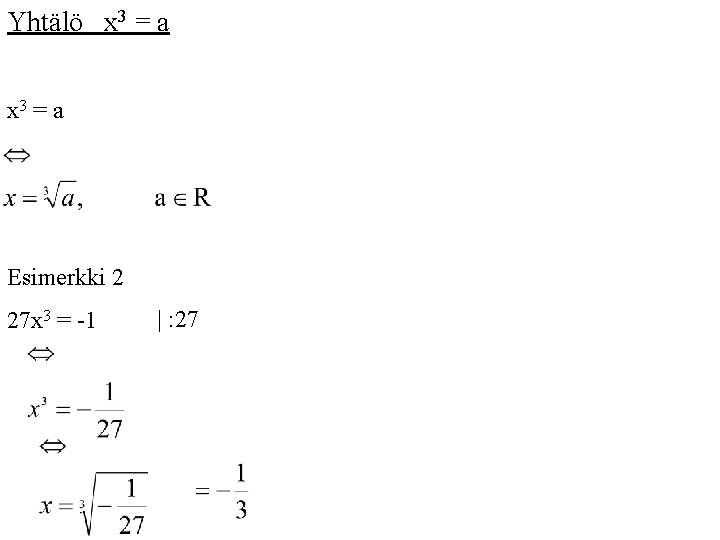

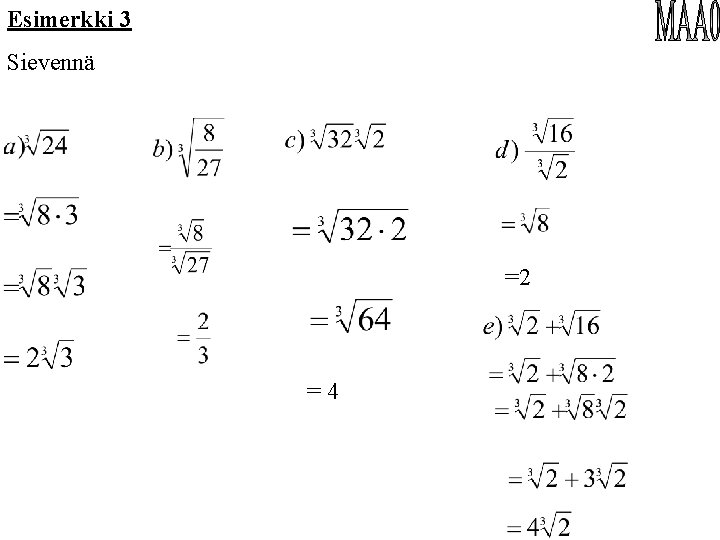





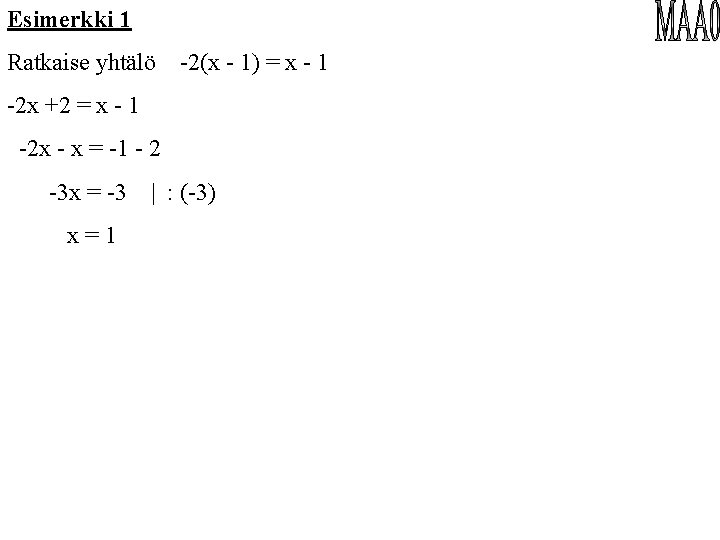




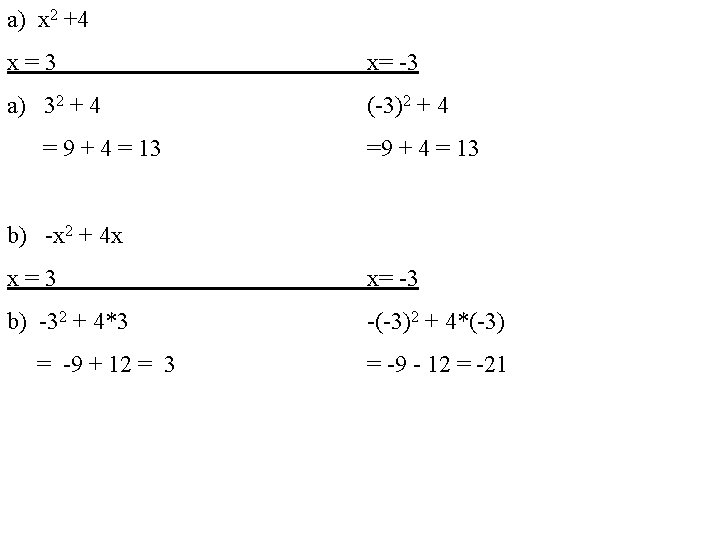
- Slides: 57

LUKUALUEET Luonnolliset luvut N = 0, 1, 2, 3, … Kokonaisluvut Z = … , -3, -2, -1, 0, 1, 2, 3, … Merkinnät: x kuuluu luonnollisten lukujen joukkoon x ei kuulu luonnollisten lukujen joukkoon

Rationaaliluvut Q luvut, jotka voidaan esittää murtolukuina Jokainen kokonaisluku Päättyvä desimaaliluku Päättymätön jaksollinen desimaaliluku Esimerkki 2 Esitä x supistettuna murtolukuna, kun x = 0, 444… x = 0, 444. . . 10 x = 4, 444… 10 x - x = 4, 444… - 0, 444… 9 x = 4 |: 9 x = 4/9

1. 1. 3 - 4. Laskutoimituksia rationaaliluvuilla 1. Laventaminen Osoittaja ja nimittäjä kerrotaan samalla luvulla. 2. Supistaminen Osoittaja ja nimittäjä jaetaan samalla luvulla. E. 1. Lavenna luvulla 4 E. 2. Supista

3. Kertolasku Sekamurtoluvut muutetaan ensin varsinaisiksi murtoluvuiksi. Tulon osoittajaksi osoittajien tulo ja nimittäjäksi nimittäjien tulo. Lopuksi supistetaan, jos voidaan. (Supistaa voi jo tekijöitäkin!) 4. Jakolasku Jaettava kerrotaan jakajan käänteisluvulla. Jatko kuten edellä 3: ssa E. 3. a)Laske b) E. 4. Laske

5. Yhteenlasku Murtolukuja saa laskea yhteen ja vähentää, kun niillä on sama nimittäjä. Tarvittaessa lavennetaan. Tällöin osoittajaksi tulee osoittajien summa (erotus) ja nimittäjäksi yhteinen nimittäjä E. 5. a)Laske

Laskulait Vaihdantalait Liitäntälait Osittelulaki a+b=b+a ab = ba (a + b) + c = a + (b + c) (ab)c = a(bc) a(b + c) =ab + ac Tulon nollasääntö 2(3 x+1) = 2∙ 3 x + 2∙ 1 =6 x + 2 ab = 0, jos ja vain jos a = 0 tai b = 0

Vastaluku Luvun a vastaluku on -a Vastalukujen summa on nolla: a + (-a) = 0 Käänteisluku Luvun a käänteisluku on 1/a (a 0) Käänteislukujen tulo on yksi: a ∙ 1/a = 1, a 0 Esimerkki 4 Määritä a) Luvun -8 vastaluku b) 2/3 käänteisluku a) 8, sillä -8 + 8 = 0. Siis -(-8) = 8 b) 3/2, sillä

Vastaluvun ominaisuuksia -(-a) = a -(a + b) = -a - b = a + (-b) a(-b) = (-a)b = -ab (-a)(-b) = ab a(b - c) = ab - ac Esimerkki 5 a) 2 * (-4) *(-5) = 40 b) 6(2 x - 4) = 12 x - 24 c) (-2)4 = 16 d) (-2)5 = -32

Likiarvot Merkitseviä numeroita Kaikki muut paitsi desimaaliluvun alussa olevat nollat Kokonaisluvun lopussa olevien nollien merkitsevyys riippuu asiayhteydestä Esimerkki 6 Kuinka monta merkitsevää numeroa on a) 2001 4 b) 0, 0023 2 c) 32 000 2 / 5, esimerkiksi asukasluku / pankkilaina

Laskeminen likiarvoilla Tulos ilmoitetaan niin monen merkitsevän numeron tarkkuudella kuin niitä on epätarkimmassa lähtöarvossa Jos kyse ainoastaan yhteen- tai vähennyslaskusta, vastaus ilmoitetaan niin monen desimaalin tarkkuudella kuin niitä on epätarkimmassa lähtöarvossa Esimerkki 7 Likiarvoille a) 1, 03 * 2, 5 = 2, 575 2, 6 b) 2, 30 + 120, 1 122, 4

1. 2. 3. Itseisarvo *luvun etäisyys nollasta Siis • positiivisen luvun itseisarvo on luku itse • negatiivisen luvun itseisarvo on luvun vastaluku • nollan itseisarvo on nolla
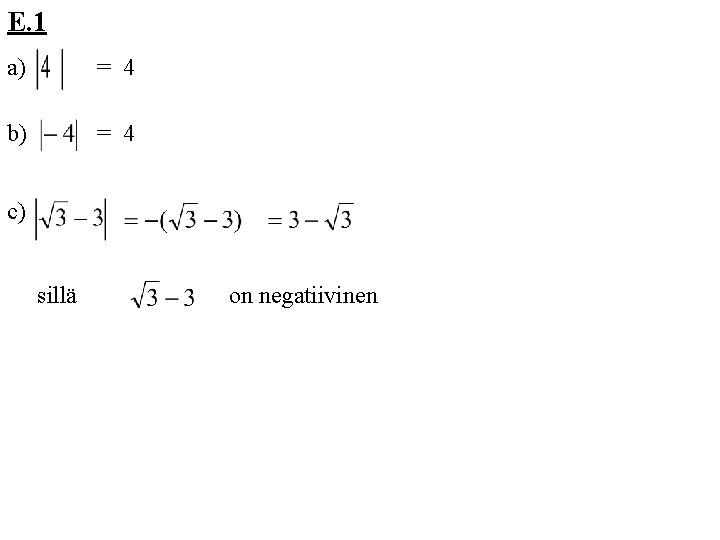
E. 1 a) = 4 b) = 4 c) sillä on negatiivinen

PROSENTTILASKUJA PROSENTTI 1%= PROMILLE = 0, 01 1) p% luvusta a 1‰= = 0, 001

Esimerkki 1 Pesuaineessa on 8 % fosforia? Kuinka paljon sitä on 1500 grammassa? tai 0, 08 * 1500 g = 120 g Muunnetaan p% desimaaliluvuksi Kerrotaan luku a tällä desimaaliluvulla

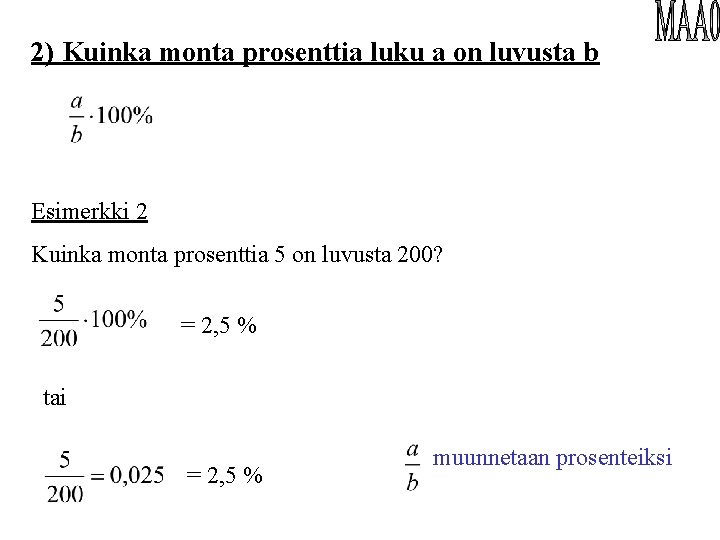
2) Kuinka monta prosenttia luku a on luvusta b Esimerkki 2 Kuinka monta prosenttia 5 on luvusta 200? = 2, 5 % tai = 2, 5 % muunnetaan prosenteiksi

3) p% lukua a suurempi luku Esimerkki 3 Mikä luku on 4 % suurempi kuin 25? 1, 04 * 25 = 26

4) p% lukua a pienempi luku Esimerkki 4 Mikä luku on 4 % pienempi kuin 25? 0, 96 * 25 = 24

5) Kuinka monta prosenttia luku a on suurempi kuin luku b a>b>0 Esimerkki 5 Kuinka monta prosenttia luku 15 on suurempi kuin 12? 15 -12 = 3

6) Kuinka monta prosenttia luku b on pienempi kuin luku a a>b>0 Esimerkki 6 Kuinka monta prosenttia luku 12 on pienempi kuin 15? 15 -12 = 3

Esimerkki 7 Vaaleissa erästä puoluetta kannatti 12 % Edellisellä kerralla kannatus oli ollut 8 %. Kuinka monta prosenttiyksikköä kannatus oli muuttunut? 12 - 8 = 4 4 prosenttiyksikköä

Esimerkki 8. Korko 4, 5 % Kuinka suuri talletuksen on oltava, jotta korko olisi 180 € vuodessa? x = talletuksen määrä 0, 045 * x = 180 : 0, 045 x = 4000 V: 4000 €

Kirjan esimerkki Lääkeliuoksen väkevyys 10%. Litra liuosta Kuinka paljon vettä on lisättävä, jotta saadun liuoksen väkevyys 4 % x = lisättävän veden määrä Liuos Väkevyys Määrä (l) Lääkkeen määrä Vanha 10 % 1 0, 1 1+x 0, 04(1+x) Uusi 4% 0, 04(1+x) = 0, 1 0, 04 + 0, 04 x = 0, 1 -0, 04 x = 0, 06 | : 0, 04 x = 1, 5 (l)

Kirjan esimerkki Työntekijöiden palkkoja korotettiin 10 % Tämän jälkeen palkkoja alennettiin 10 % Työntekijöiden alkuperäinen palkka = 100 a I: 1, 1* 100 a = 110 a II: 0, 9 * 110 a = 99 a Tämä on 99 % alkuperäisestä palkasta, joten palkka ei ole sama kuin alussa vaan 1 % pienempi (10 % otettiin eri luvuista!!!!!)

Suoraan verrannollisuus * Suureiden suhde pysyy vakiona ts. suureet muuttuvat samassa suhteessa x y x 1 y 1 x 2 y 2 kerrotaan ristiin x 1 y 2 = x 2 y 2 Jos muuttujat y ja x suoraan verrannollisia, niin y = kx (k = verrannollisuuskerroin) kuvaaja origon kautta kulkeva suora

Esimerkki 1 Ratkaise verranto 2 x = 3*5 2 x = 15 |: 2 x = 7½

Esimerkki 2 15 kg porkkanoita maksaa 34, 50 mk. a) Kuinka paljon maksaa 11 kg porkkanoita b) Muodosta porkkanoiden määrän x ja hinnan y välinen yhtälö a) 15 11 = 34, 50 y 15 y = 11 *34, 50 15 y = 379, 50 : 15 y = 25, 30 V: 25, 30 mk b) 15 x = 34, 50 y 15 y = 34, 50 x |: 15 y = 2, 3 x

Esimerkki 3 Auton jarrutusmatka on suoraan verrannollinen nopeuden neliöön. Auto pysähtyi nopeudesta 80 km/h 35 metrin matkalla. Kuinka pitkä jarrutusmatka vähintään tarvitaan pysäyttämään nopeudesta 50 km/h? 802 x = 502 *35 6400 x = 87500 |: 6400 x 14 V: 14 m

Kääntäen verrannollisuus * Suureet muuttuvat käänteisessä suhteessa * Suureiden tulo pysyy vakiona x y x 1 y 1 x 2 y 2 ELI x 1 y 1 =x 2 y 2 Jos muuttujat x ja y ovat kääntäen verrannollisia, niin y= (k = verrannollisuuskerroin) kuvaaja hyperbeli

Esimerkki 4 Viisi maalaria maalasi talon seitsemässä tunnissa. Kuinka monta maalaria tarvitaan, jotta työ valmistuisi kahdessa tunnissa? Työn kesto (h) maalareiden lukumäärä 7 5 2 x 7 2 = x 5 2 x = 35 : 2 x = 17, 5 V: 18 maalaria

POTENSSIT eksponentti kantaluku an = a ·a · ·a n Z+ n kpl Esim 1 a) 34 = 3 · 3 · 3 = 81. b) (-2)4 = (-2) ·(-2) = 16 c) -24 = -(2 · 2 · 2) = -16 d) (-2)3 = -2 · (-2) ·(-2) = -8 e) 31 =3 f) 05 =0

POTENSSIN LASKUSÄÄNTÖJÄ 1) am ∙ an = am+n Esimerkki 2 a) x 3 · x 2 = x 3+2 = x 5 3) (ab)n = an bn c) (2 x)3 = 23 x 3 = 8 x 3 5) (am)n = amn e) (x 3)4 = x 12

Esimerkki 3 = 6 x 2 Käytetään kaavaa (ab)n = an bn käänteiseen suuntaan c) 0, 01999 · 100999 =(0, 01 · 100)999 =1999 = x 9 -7 = x 2 =1

Nollas ja negatiivinen potenssi a 0 = 1, a 0 siis 00 ei ole määritelty

Esimerkki 4 a) 50 =1 b) 2 -3 c) 4 -1 Eli kun luku korotetaan potenssiin -1, niin saadaan luvun käänteisluku Kun eksponentti on 0 tai negatiivinen, niin potenssin laskulait säilyvät

Kymmenpotenssimuoto a· 10 n, missä 1 a 10 ja n Z Kerroin on ykkösen ja kymmenen välillä sekä eksponentti kokonaisluku Esimerkki 1 Tarkista laskin a) 320 000 000 290 1, 24 · 1027 = 3, 2 · 1011 b) 0, 000 232 = 2, 32 · 10 -7 2 -90 8, 08 · 10 -28 32 000 000 / 16 000 000 = 2000 3, 2 EXP 13 / 1, 6 EXP 10 3, 2 x 1013 / 1, 6 x 1010

Neliöjuuri Luvun a neliöjuuri: Juurrettava a ei saa olla negatiivinen

Esimerkki 1 Laske neliön sivun pituus. a) b) A=9 m 2 A=14, 6 m 2 Esimerkki 2 = 0, 3 4 0 42 = 16 Ei ratkaisua reaalilukujen joukossa

Esimerkki Tutki neliöjuuren määritelmän avulla, onko i) 1234 0 ii) 12342 = 1522756 1522766 Vastaus: ei ole

Yhtälö x 2 = a Jos a < 0, niin yhtälöllä ei ole ratkaisua Jos a=0, niin yhtälön ratkaisu on x=0

Esimerkki 1 Ratkaise yhtälö a) x 2 = 9 c) 4 x 2 + 16 = 0 x = 3 b) x 2 - 121 = 0 x 2=121 x = 11 4 x 2 = -16 |: 4 x 2 = -4 ei ratkaisua reaalilukujoukossa
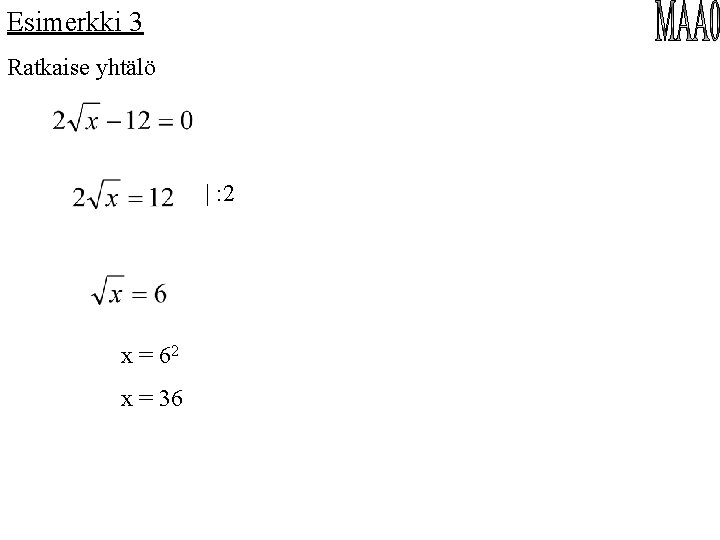
Esimerkki 3 Ratkaise yhtälö | : 2 x = 62 x = 36

Kuutio ja kuutiojuuri Luvun a kuutiojuuri: Huom. Juurrettava voi olla myös negatiivinen Siis luvun a kuutiojuuri on se luku, jonka kolmas potenssi eli kuutio on a

Esimerkki 1 23 = 8 (-3)3 = -27
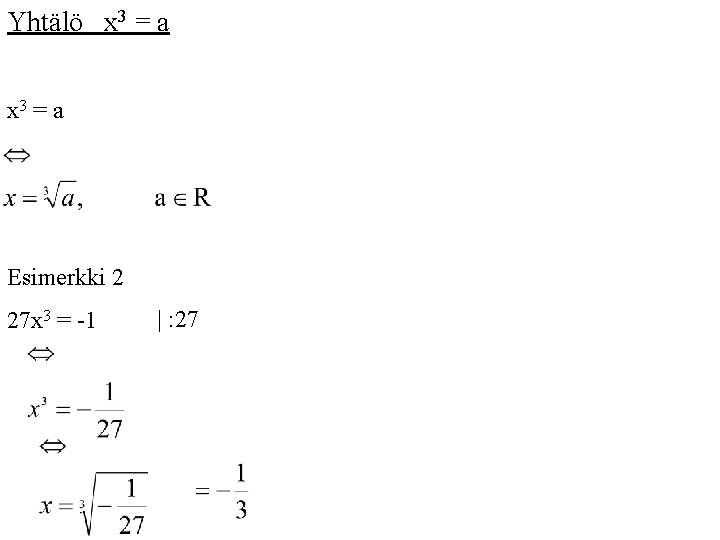
Yhtälö x 3 = a Esimerkki 2 27 x 3 = -1 | : 27

Kuutiojuuren laskusääntöjä 1. 2. 3. 4.
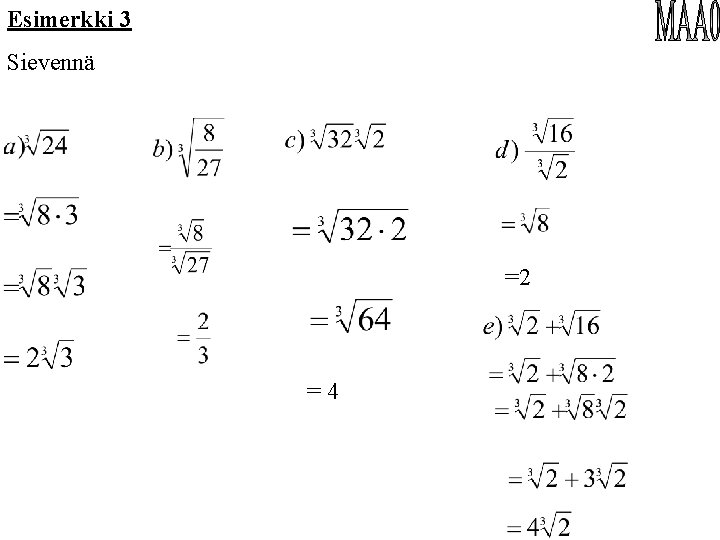
Esimerkki 3 Sievennä =2 =4

Muut juuret Parilliset juuret luetaan: n: s juuri a: sta tarkoittaa yhtälön xn = a ei negatiivista ratkaisua Parittomat juuret tarkoittaa yhtälön xn = a ratkaisua

Esimerkki 4 = 2, ei määritelty = -2, sillä 24 25 = -32 = 16 ja 2 0

Yleinen potenssi Murtopotenssi Huom. Murtopotenssit vain ei-negatiivisille kantaluvuille Murtopotenssi

Esimerkki 1 Esitä murtopotenssina Esimerkki 2 Esitä juurena

Esimerkki 3 Kirjoita luvun 2 potenssina Laske Esitä a: n potenssina =33 =27
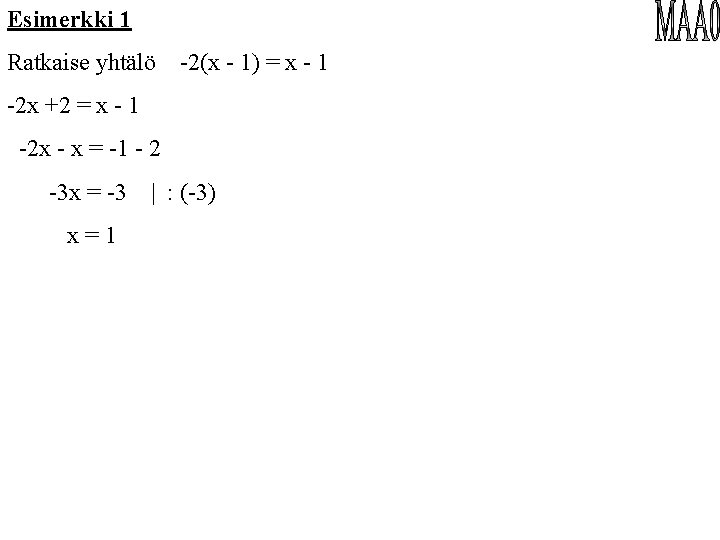
Esimerkki 1 Ratkaise yhtälö -2(x - 1) = x - 1 -2 x +2 = x - 1 -2 x - x = -1 - 2 -3 x = -3 x=1 | : (-3)

Nimittäjien poistaminen *) | 6 2(2 x - 1) - 3(4 x -2) = -6 x - 6 4 x - 2 - 12 x + 6 = -6 x - 6 4 x - 12 x + 6 x = -6 + 2 - 6 -2 x = -10 x=5 | : (-2) Tarkistus sijoitetaan x = 5 *) vasen puoli = 3 - 9 = -6 oikea puoli = -5 - 1 = -6

Onglmanratkaisu yhtälöllä Esimerkki Kolmen peräkkäisen kokonaisluvun summa on 1998. Mikä on suurin luvuista? Luvut: x x+1, x+2 x + (x+1) + (x+2) = 1998 3 x + 3 = 1998 3 x = 1998 - 3 3 x = 1995 | : 3 x = 665 Suurin luvuista: 665 + 2 = 667

Lineaarinen yhtälö ax = b, a = 0 jos a = 0, niin ratkaisuja ovat kaikki reaaliluvut tai yhtälöllä ei ole yhtään ratkaisua Esimerkki 1 Osoita, että yhtälö x(x+1) -x 2 = x toteutuu kaikilla x: n arvoilla eli on identtisesti tosi x(x+1) - x 2 = x x 2 + x -x 2 = x x-x =0 0 x = 0 0=0

Esimerkki 2 Osoita, että yhtälö x(x+1) -x 2 = x + 1 ei toteudu millään x: n arvolla eli on identtisesti epätosi x(x+1) - x 2 = x + 1 x 2 + x -x 2 = x + 1 x-x =1 0 x = 1 0=1
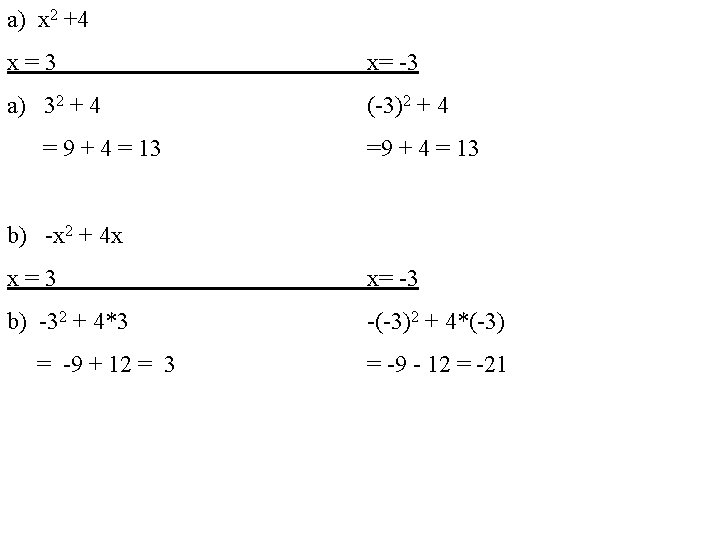
a) x 2 +4 x=3 x= -3 a) 32 + 4 (-3)2 + 4 = 9 + 4 = 13 =9 + 4 = 13 b) -x 2 + 4 x x=3 x= -3 b) -32 + 4*3 -(-3)2 + 4*(-3) = -9 + 12 = 3 = -9 - 12 = -21