LucasLehmer Primality Tester Presentation 2 Architecture Proposal February

Lucas-Lehmer Primality Tester Presentation 2: Architecture Proposal February 1, 2006 Team: W-4 Nathan Stohs W 4 -1 Brian Johnson W 4 -2 Joe Hurley W 4 -3 Marques Johnson W 4 -4 Design Manager: Prateek Goenka Overall Objective: The Testing of Prime numbers

Status • Finished – Project Chosen – C simulations – Behavioral Verilog • To Do – Floor Plan – Schematic Design – Layout – Simulaitons

Applications • Lucas-Lehmer is a test used to search for Mersenne Primes. • Mersenne Primes are primes of the form 2 p – 1 • Given p, will conclusively determine primality after p-2 iterations of the algorithm. • Computationally heavy, but numbers tested independently, so easily distributable. • Difficultly lies in choosing an implementation www. mersenne. org

Application • Mersenne primes (found with this test) are the largest prime numbers we know of today. • A pool of over 70, 000 computers currently run an implementation of this algorithm, with aggregate performance peaking at 14 Teraflops. • This is not intended to be a commercial product. • Our goal is to build a chip that uses less power

C-Code #include <stdio. h> unsigned int mod_square(int value, int mod, int p) { unsigned int mod_square(int value, int mod, int p); int acc, i; int main(int argv, char** argc) { for(acc=-2, i=0; i<(sizeof(int)*8 -1); i++) { int a = (value >> i) & 1; int temp; if (argv != 2) { printf("Usage: %s pn", argc[0]); exit(0); } if (a) { if (i-p > 0) temp = value << (i-p); else temp = value >> (p-i); int p = atoi(argc[1]); int value = 4; int i; int mod = (2 << (p-1)) - 1; for (i=1; i<=(p-2); i++) { int oldval = value; value = mod_square(value, mod, p); printf("round %d: (%d * %d - 2) mod %d = %dn", i, oldval, mod, value); } if (value == 0) printf("2^%d-1 is primen", p); else printf("2^%d-1 is not primen", p); return 0; } acc = acc + temp + ((value << i) & ((1 << p) - 1)); } if (acc >= mod) acc = acc - mod; } return acc; }

Simulation Results • Fully simulates Mersenne Primes up to 30 Using the algorithm below • Numbers above 230 make the code overflow because of the squaring in the algorithm 2 P-1 is prime if and only if Sp-2 is zero in this sequence: S 0 = 4, SN = (SN-12 - 2) mod (2 P-1) So for 27 -1: S 0 = 4 S 1 = (4 * 4 - 2) mod 127 = 14 S 2 = (14 * 14 - 2) mod 127 = 67 S 3 = (67 * 67 - 2) mod 127 = 42 S 4 = (42 * 42 - 2) mod 127 = 111 S 5 = (111 * 111 - 2) mod 127 = 0 Result says it is prime

Design Decisions • What type of adder will we use? • Should we broaden the scope of our project? • Do we get into mod multiply and mod add for (2 p+1)?

Significance of (2 p+1) • As previously stated (2 p-1) finds Mersenne Primes • (2 p+1) however, can be used to find Fermat numbers • This form is also used for encryption

Adder Options • Parallel-prefix Adders – Serial-Prefix, which is the smallest but slowest – Sklansky parallel-prefix, which is the fastest but lager • End-around Carry-Adders – Some take 2 propagations in series, which is slow – Faster ones require two adders and a multiplexer, which is big

Modulo Multiply (2 n-1) • Has to do with partial products • The algorithm calls for a Mod every time that there is a chance • Example: Mod 127 23 X 56 Leave 18 Leave 120 150 Mod 1000 Mod

Verilog Code module mod_square( value, mod, p, newvalue ); input [31: 0] value, mod, newvalue; input [4: 0] p; reg [31: 0] acc=-2; reg [31: 0] temp; reg a; acc=-2; initial begin for(i=0; i<31; i = i + 1) begin a = (value >> i) & 1; if (a) begin if (i-p > 0) temp = value << (i-p); else temp = value >> (p-i); acc = acc + temp + ((value << i) & ((1 << p) - 1)); end if (acc >= mod) acc = acc - mod; end

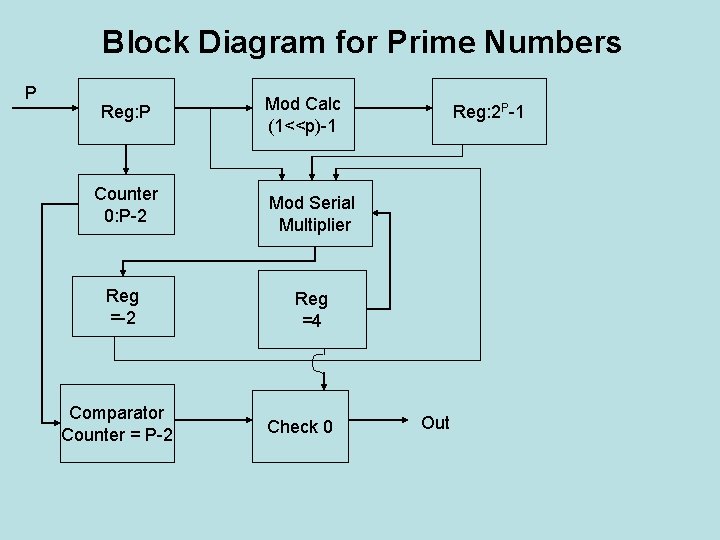
Block Diagram for Prime Numbers P Reg: P Mod Calc (1<<p)-1 Counter 0: P-2 Mod Serial Multiplier Reg =-2 Reg =4 Comparator Counter = P-2 Check 0 Reg: 2 P-1 Out

Simulation Results • Fully simulates Mersenne Primes up to 30 Using the algorithm below • Numbers above 230 make the code overflow because of the squaring in the algorithm 2 P-1 is prime if and only if Sp-2 is zero in this sequence: S 0 = 4, SN = (SN-12 - 2) mod (2 P-1) So for 27 -1: S 0 = 4 S 1 = (4 * 4 - 2) mod 127 = 14 S 2 = (14 * 14 - 2) mod 127 = 67 S 3 = (67 * 67 - 2) mod 127 = 42 S 4 = (42 * 42 - 2) mod 127 = 111 S 5 = (111 * 111 - 2) mod 127 = 0 Result says it is prime

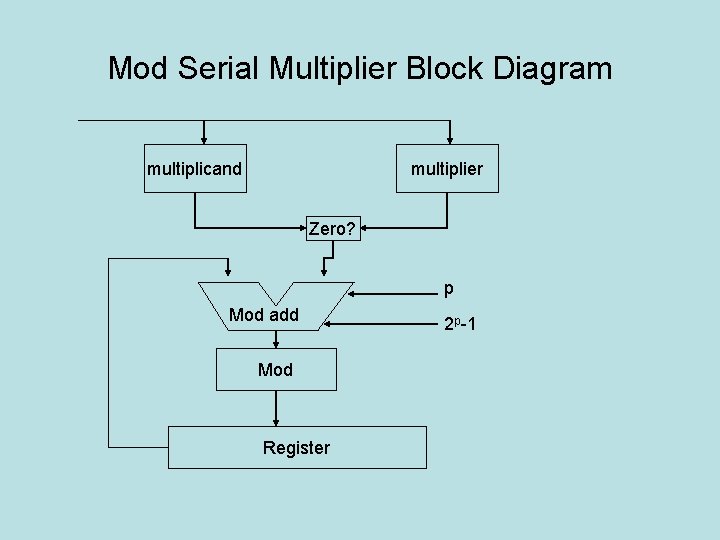
Mod Serial Multiplier Block Diagram multiplicand multiplier Zero? p Mod add Mod Register 2 p-1

What’s Next • Continue researching adders • Choose which adder to use • Decide if we will broaden the scope of our project • Start doing layout

Problems • Prime numbers do not get interesting until P is in the thousands • Up to P=32 we could use Registers • If we want to take this to the next level we need to use SRAM but will that make this too big of a project?

Questions?