LucasKanade Image Alignment Iain Matthews Paper Reading Simon

Lucas-Kanade Image Alignment Iain Matthews

Paper Reading Simon Baker and Iain Matthews, Lucas-Kanade 20 years on: A Unifying Framework, Part 1 http: //www. ri. cmu. edu/pub_files/pub 3/baker_simon_2002_3. pdf And Project 3 Description

Recall - Image Processing Lecture • Some operations preserve the range but change the domain of f : What kinds of operations can this perform? • Still other operations operate on both the domain and the range of f.

Face Morphing

Applications of Image Alignment • Ubiquitous computer vision technique • • • Mosaicing Tracking Parametric and layered motion estimation Image registration and alignment Face coding / parameterization Super-resolution

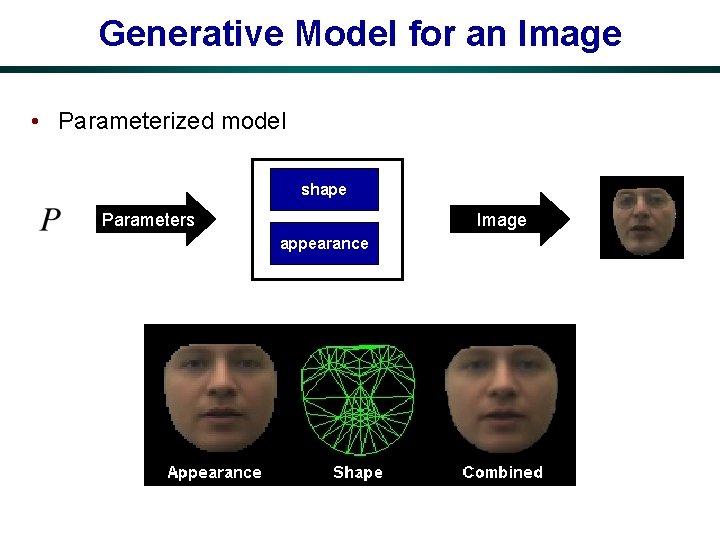
Generative Model for an Image • Parameterized model shape Parameters Image appearance

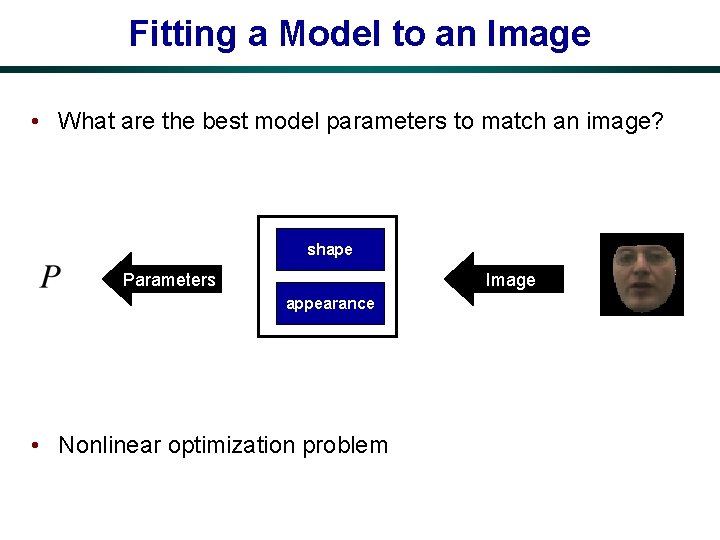
Fitting a Model to an Image • What are the best model parameters to match an image? shape Parameters Image appearance • Nonlinear optimization problem

Active Appearance Model Shape Landmarks Appearance Warp to reference Region of interest • Cootes, Edwards, Taylor, 1998

Image Alignment Template, T(x) Warp, W(x; p+ p) Warp, W(x; p) Image coordinates x = (x, y)T Warp parameters, p = (p 1, p 2, …, pn)T Image, I(x)

Want to: Minimize the Error • Warp image to get Template, T(x) Warped, I(W(x; p)) T(x) - I(W(x; p)) compute

How to: Minimize the Error Minimise SSD with respect to p, Generally a nonlinear optimisation problem Solution: solve for increments to current estimate, =

Linearize Taylor series expansion, linearize function f about x 0: For image alignment:

Gradient Descent Solution Least squares problem, solve for p Solution, Error Image Gradient Hessian Jacobian

Gradient Images • Compute image gradient W(x; p) Ix I(W(x; p)) Iy

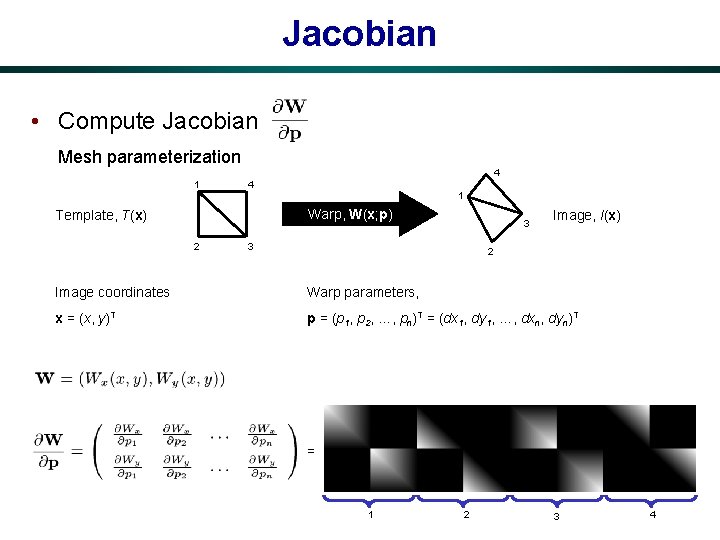
Jacobian • Compute Jacobian Mesh parameterization 4 1 Warp, W(x; p) Template, T(x) 2 3 3 Image, I(x) 2 Image coordinates Warp parameters, x = (x, y)T p = (p 1, p 2, …, pn)T = (dx 1, dy 1, …, dxn, dyn)T = 1 2 3 4

Lucas-Kanade Algorithm 1. Warp I with W(x; p) I(W(x; p)) 2. Compute error image T(x) - I(W(x; p)) 3. Warp gradient of I to compute I 4. Evaluate Jacobian 5. Compute Hessian 6. Compute p 7. Update parameters p p + p - =

Fast Gradient Descent? • To reduce Hessian computation: 1. Make Jacobian simple (or constant) 2. Avoid computing gradients on I

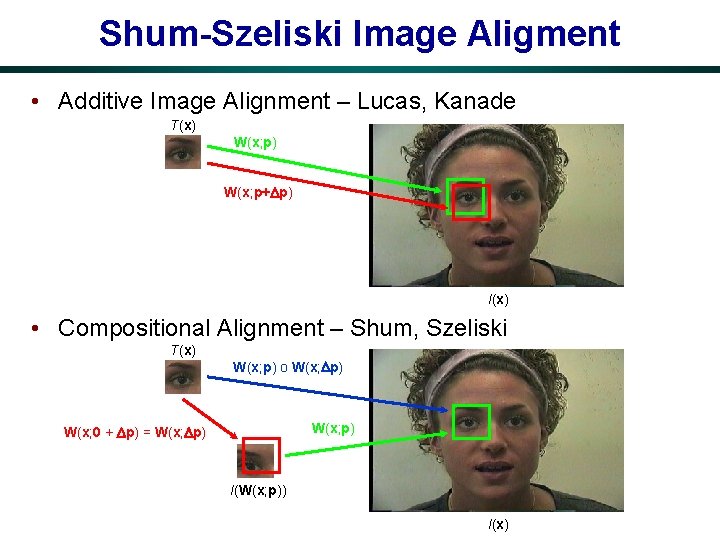
Shum-Szeliski Image Aligment • Additive Image Alignment – Lucas, Kanade T(x) W(x; p+ p) I(x) • Compositional Alignment – Shum, Szeliski T(x) W(x; p) o W(x; p) W(x; 0 + p) = W(x; p) I(W(x; p)) I(x)

Compositional Image Alignment Minimise, T(x) W(x; p) o W(x; p) I(W(x; p)) I(x) Jacobian is constant, evaluated at (x, 0) “simple”.

Compositional Algorithm 1. Warp I with W(x; p) I(W(x; p)) 2. Compute error image T(x) - I(W(x; p)) 3. Warp gradient of I to compute I 4. Evaluate Jacobian 5. Compute Hessian 6. Compute p 7. Update W(x; p) o W(x; p) - =

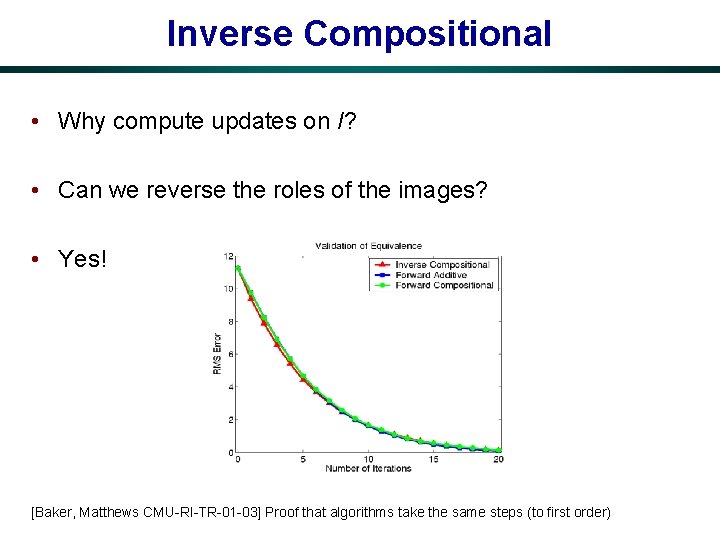
Inverse Compositional • Why compute updates on I? • Can we reverse the roles of the images? • Yes! [Baker, Matthews CMU-RI-TR-01 -03] Proof that algorithms take the same steps (to first order)

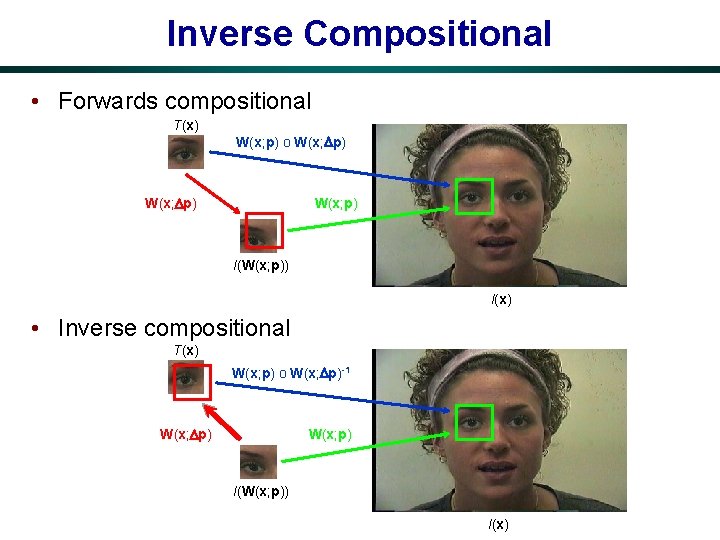
Inverse Compositional • Forwards compositional T(x) W(x; p) o W(x; p) I(W(x; p)) I(x) • Inverse compositional T(x) W(x; p) o W(x; p)-1 W(x; p) I(W(x; p)) I(x)

Inverse Compositional • Minimise, • Solution • Update

Inverse Compositional • Jacobian is constant - evaluated at (x, 0) • Gradient of template is constant • Hessian is constant • Can pre-compute everything but error image!

Inverse Compositional Algorithm 1. Warp I with W(x; p) I(W(x; p)) 2. Compute error image T(x) - I(W(x; p)) 3. Warp gradient of I to compute I 4. Evaluate Jacobian 5. Compute Hessian 6. Compute p 7. Update W(x; p) o W(x; p)-1 - =

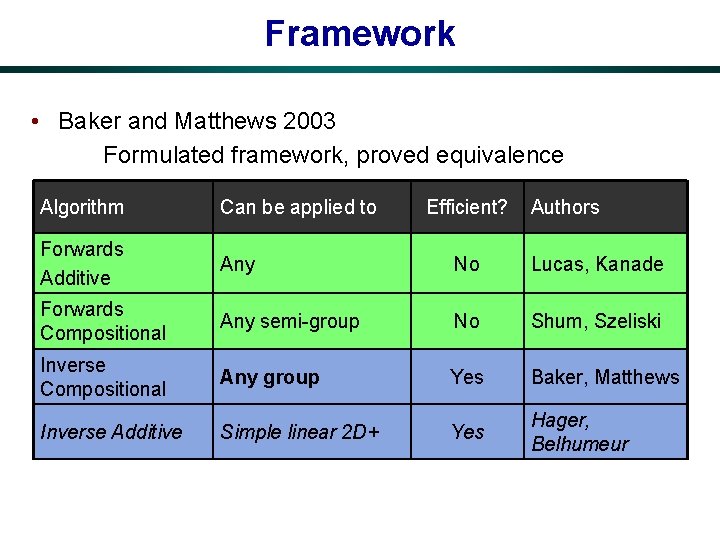
Framework • Baker and Matthews 2003 Formulated framework, proved equivalence Algorithm Can be applied to Efficient? Authors Forwards Additive Any No Lucas, Kanade Forwards Compositional Any semi-group No Shum, Szeliski Inverse Compositional Any group Yes Baker, Matthews Inverse Additive Simple linear 2 D+ Yes Hager, Belhumeur

Example