LShaped RST Routing n Perform LRST using node

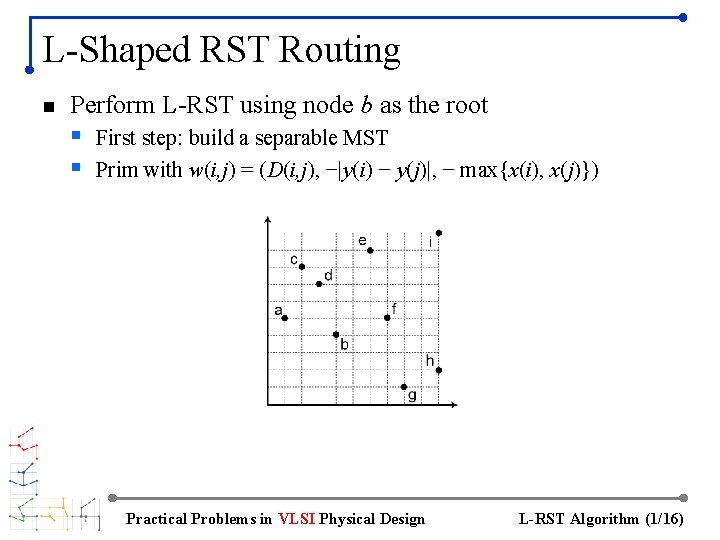
L-Shaped RST Routing n Perform L-RST using node b as the root § First step: build a separable MST § Prim with w(i, j) = (D(i, j), −|y(i) − y(j)|, − max{x(i), x(j)}) Practical Problems in VLSI Physical Design L-RST Algorithm (1/16)

First Iteration Practical Problems in VLSI Physical Design L-RST Algorithm (2/16)

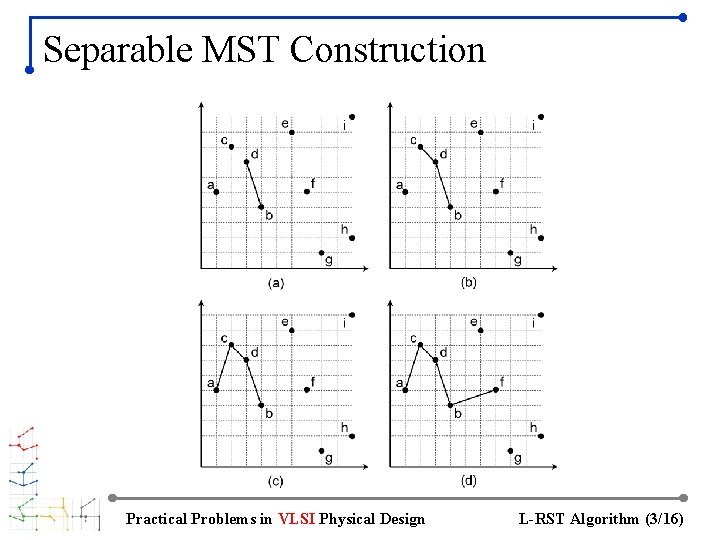
Separable MST Construction Practical Problems in VLSI Physical Design L-RST Algorithm (3/16)

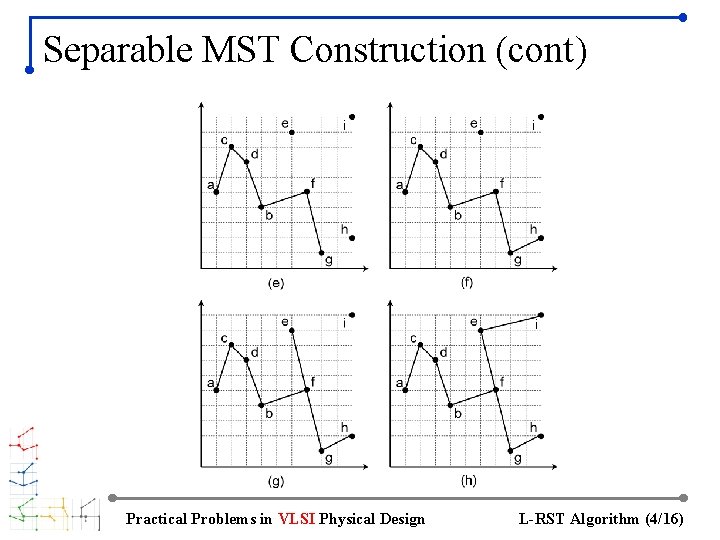
Separable MST Construction (cont) Practical Problems in VLSI Physical Design L-RST Algorithm (4/16)

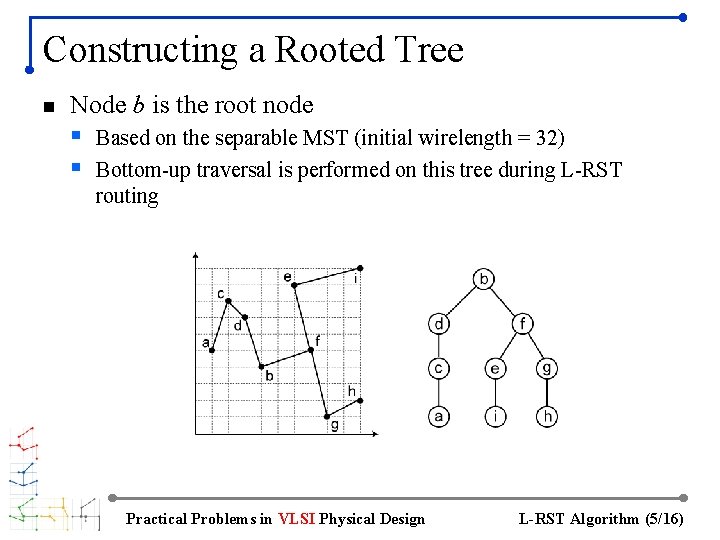
Constructing a Rooted Tree n Node b is the root node § Based on the separable MST (initial wirelength = 32) § Bottom-up traversal is performed on this tree during L-RST routing Practical Problems in VLSI Physical Design L-RST Algorithm (5/16)

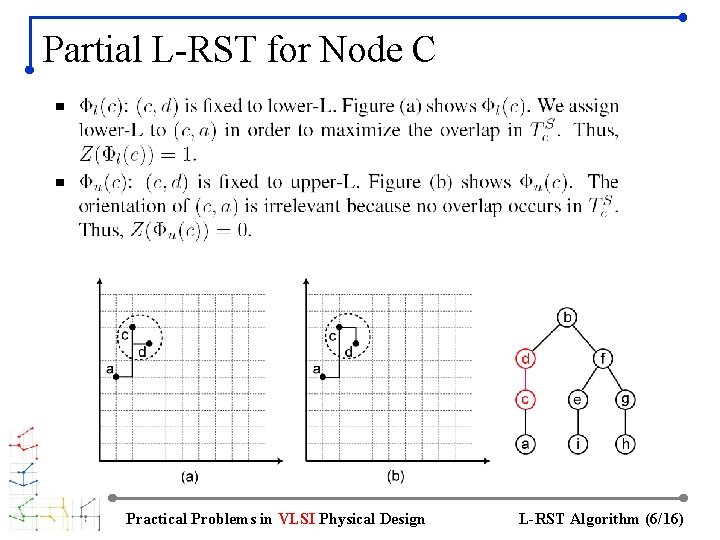
Partial L-RST for Node C Practical Problems in VLSI Physical Design L-RST Algorithm (6/16)

Partial L-RST for Node E Practical Problems in VLSI Physical Design L-RST Algorithm (7/16)

Partial L-RST for Node G Practical Problems in VLSI Physical Design L-RST Algorithm (8/16)

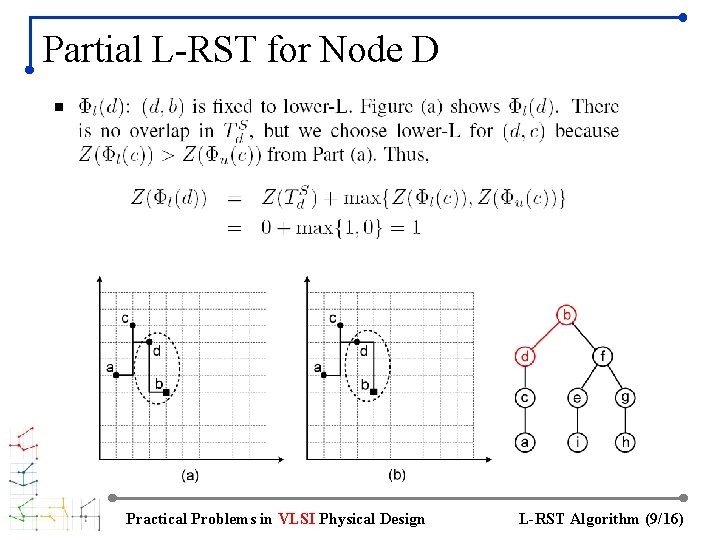
Partial L-RST for Node D Practical Problems in VLSI Physical Design L-RST Algorithm (9/16)

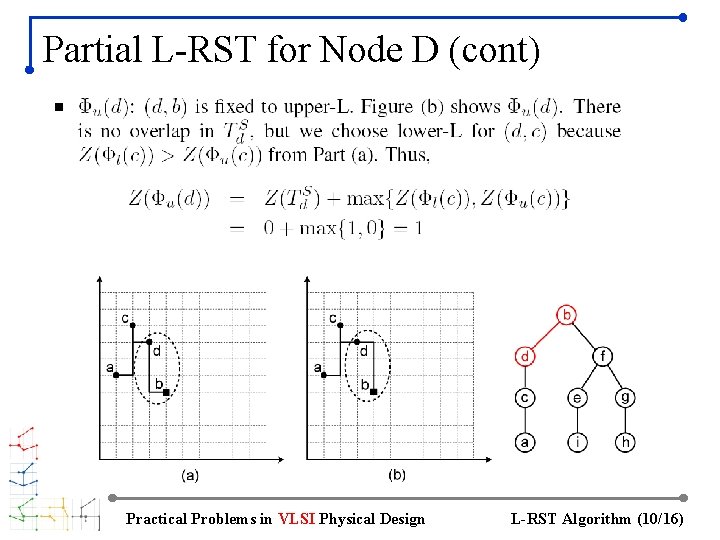
Partial L-RST for Node D (cont) Practical Problems in VLSI Physical Design L-RST Algorithm (10/16)

Partial L-RST for Node F best case Practical Problems in VLSI Physical Design L-RST Algorithm (11/16)

Partial L-RST for Node F (cont) best case Practical Problems in VLSI Physical Design L-RST Algorithm (12/16)

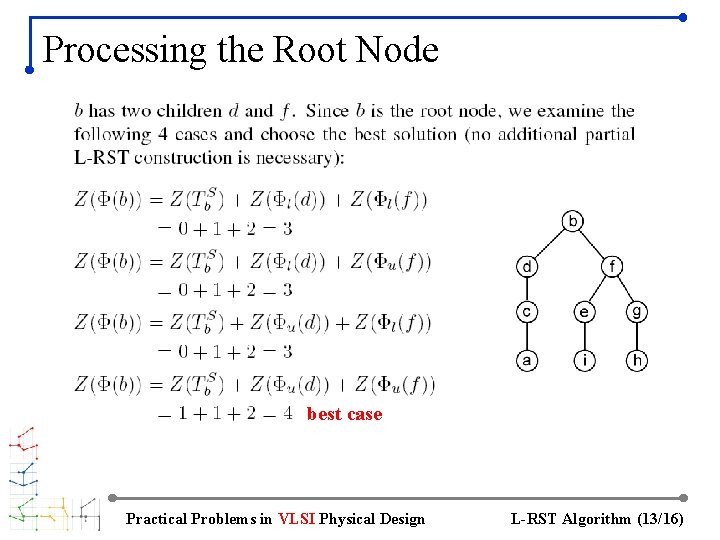
Processing the Root Node best case Practical Problems in VLSI Physical Design L-RST Algorithm (13/16)

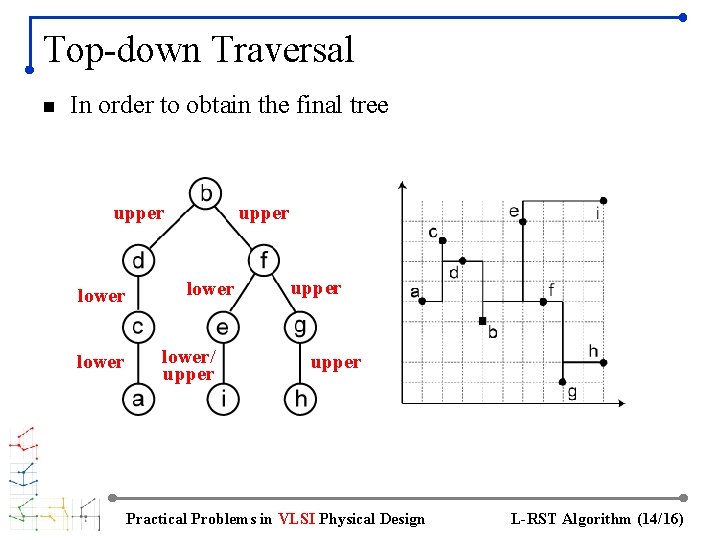
Top-down Traversal n In order to obtain the final tree upper lower/ upper Practical Problems in VLSI Physical Design L-RST Algorithm (14/16)

Final Tree n Wirelength reduction § Initial wirelength − total overlap = 32 − 4 = 28 Practical Problems in VLSI Physical Design L-RST Algorithm (15/16)

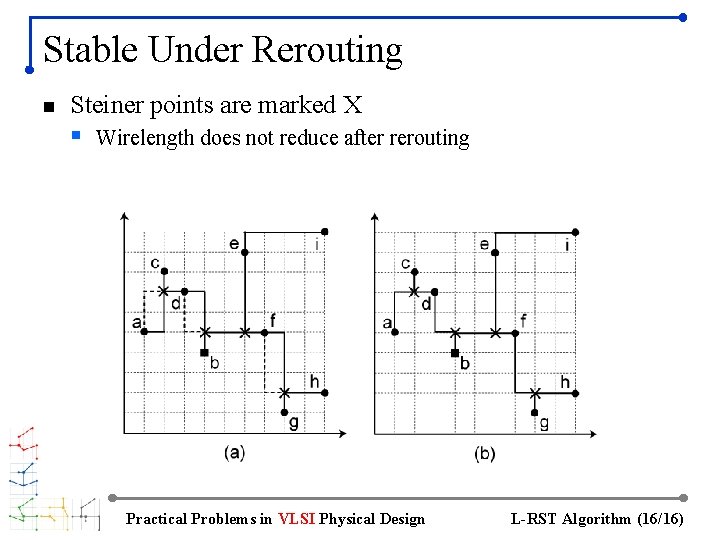
Stable Under Rerouting n Steiner points are marked X § Wirelength does not reduce after rerouting Practical Problems in VLSI Physical Design L-RST Algorithm (16/16)