Lringsml i relation til linere funktioner ved overgang

Læringsmål i relation til lineære funktioner ved overgang fra grundskole til gymnasium Morten Blomhøj IMFUFA, INM, RUC Overgangsprojektet Roskilde 30. oktober 2018

Plan 1. Lineære funktioner – et vigtigt emne 2. Hvad kan forskningen bidrag med? 3. Undersøgende matematikundervisning som middel til udvikling af begrebsforståelse 4. Opsamling - begrebskort 5. Spørgsmål og diskussion – også gerne undervejs

1. Lineære funktioner - vigtigt i emne for sammenhængen • Det er her eleverne for første gang møde formalisering af sammenhænge mellem variable (7. kl. ). • Der bygges videre på begreber om variabel, ligning og koordinatsystem. • Der arbejdes for første gang med kontinuerte variable. • Der arbejdes med algebraiske repræsentationer i form af ligninger med to variable (y = ax + b) , og deres sammenhænge med tabeller, grafer og sproglige repræsentationer. • Funktionsbegrebet introduceres, repræsenteres symbolsk (y = f(x)) og anvendes i forskellige sammenhænge.

• Emnet giver mulighed for, at eleverne kan arbejde med matematisk problemløsning og modellering. • Lineære funktioner har mange anvendelser i andre fag og kan forbindes til elevernes erfaringer i mange situationer. • Det rummer rige muligheder for at arbejde med generelle digitale matematikværktøjer. • Emnet er vigtigt som grundlag for den fortsatte teoriopbygning i matematik. Det gælder i særlig grad i forhold til funktionsbegrebet generelt og som grundlag for differential- og integralregning. • Lineære funktioner volder eleverne læringsmæssige vanskeligheder ved overgangen fra grundskole til ungdomsuddannelserne – måske især de gymnasiale.

Trinmål 7. -9. klasse for algebra og funktioner Fase 3 (Ligninger): Eleven kan opstille og løse enkle ligningssystemer og har viden om grafisk løsning af enkle ligningssystemer. Fase 3 (Formler og algebra): Eleven kan sammenligne algebraiske udtryk og har viden om regler for regning med reelle tal. Fase 1 (Funktioner): Eleven kan anvende lineære funktioner til at beskrive sammenhænge og forandringer og har viden om repræsentationer for lineære funktioner Fase 2 (Funktioner): Det samme for (simple) ikke-lineære funktioner! www. emu. dk

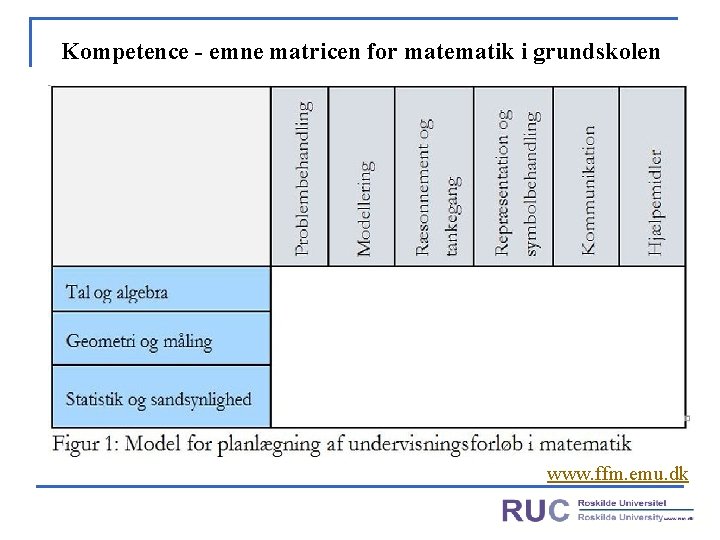
Kompetence - emne matricen for matematik i grundskolen www. ffm. emu. dk

Nogle resultater fra en undersøgelse i en 9. klasse y = x + 5 Hvad kan du sige om x i forhold til y? 6 ud af 22 svarede rigtigt. 7 besvarelser angav, at x er 5 større end y som i disse tre: (1) x er altid 5 større end y. Hvis man tegner en graf vil linjen gå igennem +5. (2) x 0 1 2 y 5 6 7 x er altid 5 større end y. (3) x er altid 5 et eller andet højere, større eller flere end y. Eller x er altid = y+5 (Blomhøj, 1997)

Alle 7 elever med besvarelser, der indeholder udsagnet ”x er 5 større end y” havde besvaret følgende opgave helt korrekt: Tegn grafen for funktionen givet ved ligningen: y = 2 x + 3. Der findes elever, der kan løse førstegradsligninger enten i hånden eller med CAS uden, at de derefter er i stand til at afgøre om en given værdi af x er en løsning til den ligning de lige selv har løst! • Løs ligningen: 7 x – 3 = 13 x + 15 • Er 10 en løsning til ligningen: 7 x – 3 = 13 x + 15

1. hovedsætning i matematikkens didaktik For den enkelte elev/studerende får et matematisk begreb ikke større anvendelsesdomæne eller flere relationer til andre begreber end det domæne og de relationer, der udspændes af den pågældendes personlige erfaringer med begrebet. Og det gælder uanset hvilke formelle begrebsdefinitioner eleven/studenten undervises i. (Niss, 1999)

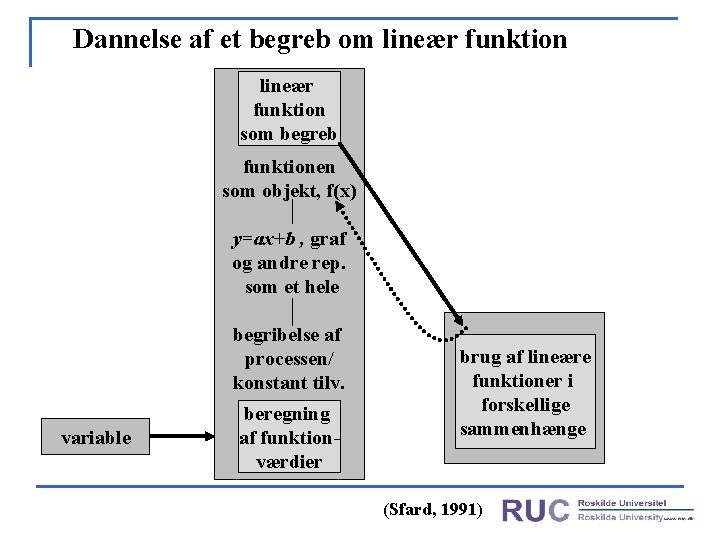
En model for dannelse af matematiske begreber Udviklet af Anna Sfard (1991). A. Procesforståelse går forud for objektforståelse. B. Processen forløber gennem tre faser: (1) Internalisering, (2) Kondensering og (3) Tingsliggørelse. C. Tilegnelse af et matematisk begreb omfatter både proces og objekt forståelse og muligheden for at skifte mellem dem. Proces og objekt aspekterne kan ikke udvikles samtidig, men kan opfattes som komplementære i læreprocessen.

Dannelse af et begreb om lineær funktion som begreb funktionen som objekt, f(x) y=ax+b , graf og andre rep. som et hele begribelse af processen/ konstant tilv. variable beregning af funktionværdier brug af lineære funktioner i forskellige sammenhænge (Sfard, 1991)

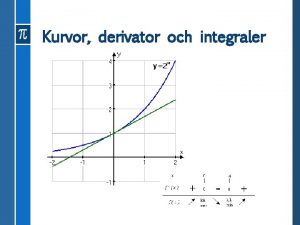
Matematiske begreber og deres repræsentationer Dens repræsentation (tegn/symbol) En lineær funktion: (objekt) y = -2 x+5, x R Lineær funktion (begreb) (Steinbring, 2005)

Proces og objekt repræsentationer af lineære funktioner Repræsenta- Sproglig tionsform Numerisk Proces Jeg er fem år ældre end min bror. y-værdien fås f(x+1)=f(x)+1 ved at lægge 5 f(0)=5 til x-værdien. y fås ved at gange med a og lægger b til. y er funktion f(x+ x)= af x og y=f(x) + a x; fås ved at ind- f(x 0)=y 0 sætte x-værdi. Objekt Punkter (x, y), x 0 1 2 3 hvor y er 5 y 5 6 7 8 større end x. En lineær kombination En funktionsmed konstant tabel sum. Algebraisk y=x+5 y=f(x) y = ax + b y-y 0=a(x-x 0) ux+vy=w Grafisk

Sammenhængen mellem rette linjer og lineære funktioner Funktioner med forskriften f(x) = ax + b har en ret linje som graf. a er linjens hældning og (0, b) er linjens skæringspunkt med 2. aksen. f(x+1) = a(x+1)+b = f(x) + a (y) 1 b * a * (x, y) * (x 0, y 0) En linje har samme hældning overalt: a = (y – y 0)/(x – x 0), x ≠ x 0 y – y 0= a (x – x 0) y = ax – ax 0 + y 0 y = ax + b, med b = y 0 – ax 0 er altså en generel ligning for en ikke-lodret linje, hvor a er hældningen og b skæring med 2. aksen. Ret linje (x) D 10

Opgaver der udfordre forståelse af lineær funktioner 1. Givet ligningen y = x + 5, hvad kan du sige om xværdien i forhold til y-værdien for et punkt på linjen? 2. Marker punkter i koordinatsystemet, hvor summen af punktets koordinater giver 10. (a) Tegn en graf gennem punkterne – hvad ser du? (b) Opskriv en ligning, der svarer til grafen. 3. Marker punkter i koordinatsystemet, hvor y-koordinaten er 5 større end x-koordinaten (b) Tegn en graf gennem punkterne, og angiv en ligning for sammenhængen. 4. tal, Hvis man kender summen og differensen mellem to hvordan finder man så tallene? Er der altid et entydigt svar? Opskriv ligninger og tegn grafer der forklarer svarene.

Opgaver der udfordre forståelse af lineær funktioner 5. Fremstil billeder som disse eller tilsvarende ved hjælp af et passende program. 6. Find funktionsforskrifter for fire linjer, der danne et kvadrat som ikke er parallelt med koordinatakserne. 7. Hvordan ser graferne ud for rette linjer givet ved ligningen: y = 2 x + b? (a) Sæt x=0 ind i ligningen og fortolk resultatet. (b) Sæt b=0 ind i ligningen og fortolk resultatet. 8. Hvordan ser graferne ud for rette linjer giver ved ligningen: y = ax + 3? (a) Sæt x=0 ind i ligningen og fortolk resultatet. (b) Sæt a=0 ind i ligningen og fortolk resultatet.

Opgaver der udfordre forståelse af lineær funktioner 9. Grafen for linjen med ligningen y = -2 x +3 er tegnet i et koordinatsystem, og ligningen er angivet. (a) Ligger punktet (0. 001, 3) på linjen? (b) Hvis punktet (2, a) ligger på linjen, hvilken værdi har a så? (c) Hvis punktet (z, 5) ligger på linjen, hvilken værdi har z så? (d) Hvis (3, y) ligger over linjen, hvad kan du så sige om værdien af y? 10. Kan 3 x+3=y-7 være ligningen for en ret linje? 11. Kan 3 a =-b+10 være ligningen for en ret linje? 12. Bestem ligninger for fire linjer, der tilsammen danner et kvadrat, der ikke er parallelt med koordinatakserne.

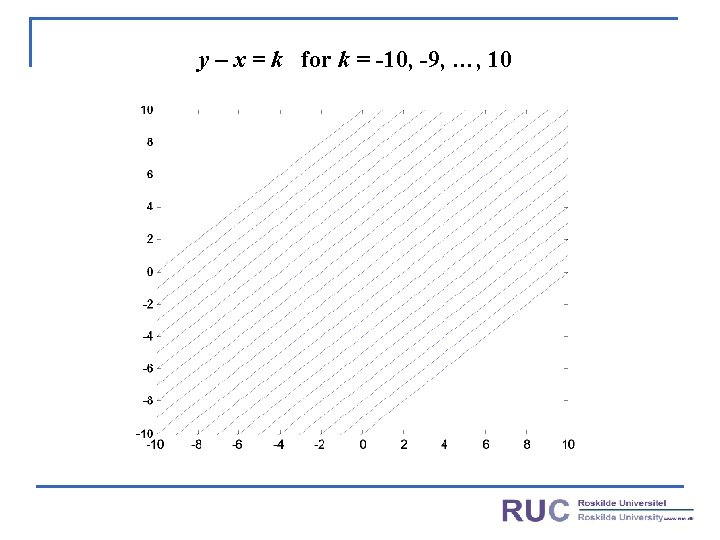
y – x = k for k = -10, -9, …, 10

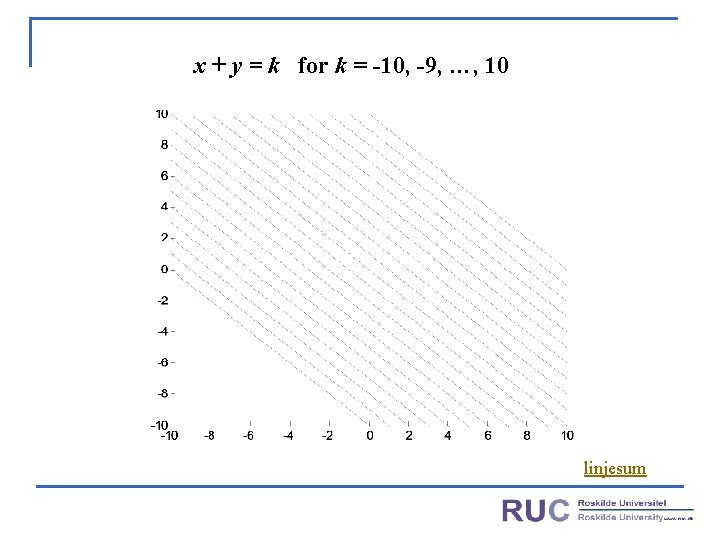
x + y = k for k = -10, -9, …, 10 linjesum

y = ax for a = tan (p�� /10) for p = 1, 2, . . , 10 D 10

Mortens brusebad: Vandforbrug som funktion af badetid 3 l koldt 6 l/min ”y = 6 x + 3. x er minutter jeg er i bad, og y er hvor mange liter vand jeg bruger. På 10 min. bruger jeg 63 l. Brusebad

Modellering af alkoholforbrænding og nedbrydning af THC For alkohol: Ind(t) A(t) [g] c [g/time] A(0) = A 0 Hvis Ind(t)=0 og A(0)=A 0, så er A(t) = A 0 – c t Det fås også af: A’(t) = - c => A(t) = A 0 – c t For THC: Ind(t) THC(t) [mg] a THC(t) [mg/time] THC(0) = THC 0 Hvis Ind(t)=0, THC’(t) = - a THC(t) => THC(t) = THC 0 e(-a t)

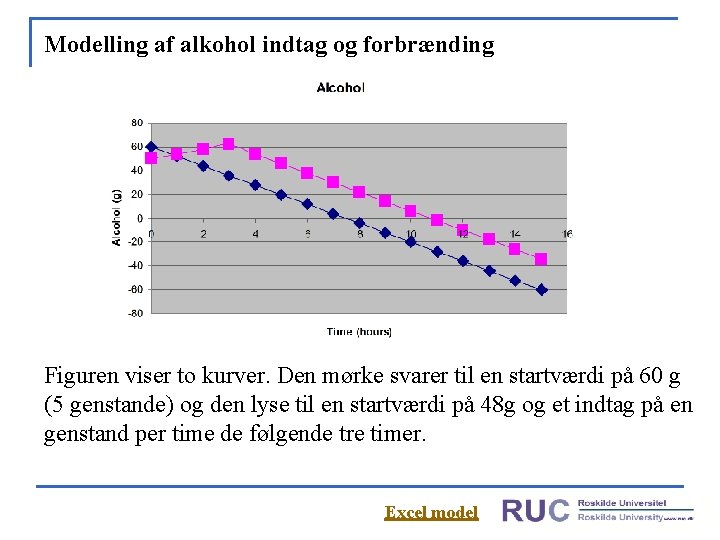
Modelling af alkohol indtag og forbrænding Figuren viser to kurver. Den mørke svarer til en startværdi på 60 g (5 genstande) og den lyse til en startværdi på 48 g og et indtag på en genstand per time de følgende tre timer. Excel model

Modellen kan repræsenteres med stykvise lineære funktioner efter “ind – ud” princippet: =>

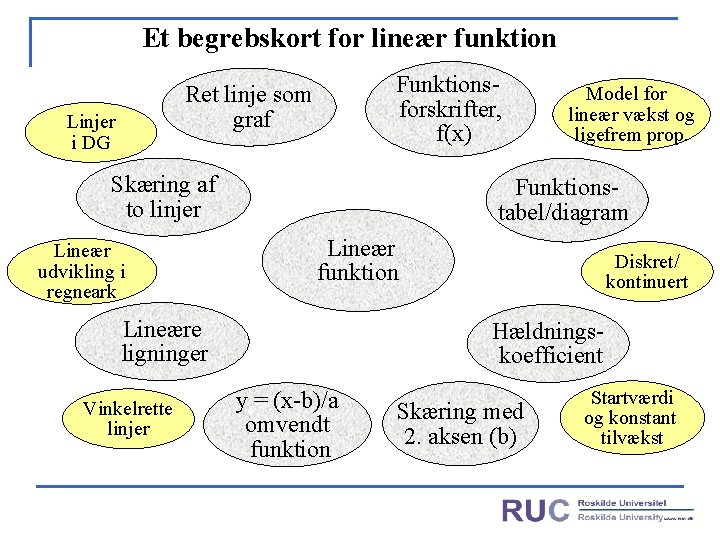
Et begrebskort for lineær funktion Funktions- forskrifter, f(x) Ret linje som graf Linjer i DG Skæring af to linjer Lineær udvikling i regneark Funktionstabel/diagram Lineær funktion Lineære ligninger Vinkelrette linjer Model for lineær vækst og ligefrem prop. Diskret/ kontinuert Hældnings koefficient y = (x-b)/a omvendt funktion Skæring med 2. aksen (b) Startværdi og konstant tilvækst

Referencer Alrø, H. og O. Skovsmose (2006 a). Undersøgende samarbejde i matematikundervisningen - udvikling af IC-modellen. I (Skovsmose og Blomhøj, 2006). Alrø, H. og O. Skovsmose (2006 b). Læring mellem dialog, intention, refleksion og kritik. I (Skovsmose og Blomhøj, 2006). Alrø, H. and O. Skovsmose (2002). Dialogue and learning in mathematics education: Intention, reflection, critique. Dordrecht: Kluwer. Alrø, H. , Blomhøj, M. , Bødtkjer, H. , Skovsmose, O. og Skånstrøm, M. : Farlige små tal – almendannelse i et risikosamfund. I (Skovsmose og Blomhøj, 2006). Artigue, M. og M. Blomhøj (2013). Conceptualising inquiry based education in mathematics. ZDM - The International Journal of Mathematical Education, 45(6) Arcavi, A. , 1994: Symbol sense: Informal sense-making in formal mathematics. For the Learning of Mathematics, 14, 3 (Nov. ), 24 -35. Bodin, A. , 1993: What does to assess mean? The case of assessing mathematical knowledge. I M. Niss (ed. ): Investigations into assessment in mathematics education, 113 -142. Dordrecht, Kluwer.

Blomhøj, M. (2016). Fagdidaktik i matematik. København: Frydenlund. Blomhøj, M. and T. Højgaard Jensen (2007). SOS-projektet – didaktisk modellering af et sammenhængsproblem. MONA, 3, s. 25 -53. Blomhøj, M. and Kjeldsen, T. H. (2010). Learning mathematics through modelling-the case of the integral concept. In First Sourcebook on Nordic Research in Mathematics Education. Information Age Publishing, incorporated. Blomhøj, M. and Kjeldsen, T. H. (2013). Students’ Mathematical Learning in Modelling Activities. In Stillman, G. , Kaiser, Blum, W. , Brown, J. (eds. ) Teaching mathematical modelling: Connecting to Research and Practice. International Perspectives on the Teaching and Learning. Dordrecht, Springer, 141 -151. Blomhøj, M. og Kjeldsen, T. H. (2014). Brug af didaktisk teori i læreres udvikling af modelleringsprojekter i matematik. MONA (2), 42 -63. Blomhøj, M. og M. Skånstrøm (2006). Matematik Morgener – matematisk modellering i praksis. I (Skovsmose og Blomhøj, 2006). Brousseau, G. , (1997): Theory of didactical situations in mathematics. Dordrecht, Kluwer. Dubinsky, E. & M. A. Mcdonald (2001): APOS: A constructivist theory of learning in undergraduate mathematics education research. I Holton, D. (Ed. ): The teaching and learning of mathematics at university level: An ICMI-study, 275 -282, Dordrecht, Kluwer.

Gravemeijer, K. , & Doorman, L. M. (1999). Context problems in realistic mathematics education: A calculus course as an example. Educational Studies in Mathematics, 39(1– 3), 111– 129. Hartmann Jensen, M. (2013). Students’ conceptual understanding of functions at upper secondary level. Speciale fra matematik på RUC. IMFUFA-tekst nr. . 496. Niss, M. (1993). Centrale problemstillinger i matematikkens didaktik i 1990’erne. I Andersen, 15. Nordiske LMFK-kongres (11 -47). Konferencerapport. Århus, LMFK. Niss, M. & Højgaard Jensen, T. (2002): Kompetencer og matematiklæring. Ideer og inspiration til udvikling af matematikundervisning i Danmark. Uddannelsesstyrelsens temahæfteserie nr. 18. Olsson, J. (2017). Geo. Gebra, Enhancing Creative Mathematical Reasoning. Doctoral thesis. Umeå University. Sfard, A. , (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational Studies in Mathematics, 22, 1 -36. Skovsmose, O. og M. Blomhøj (red. ) (2006): Kunne det tænkes? – om matematik-læring. København: Maling Beck. Skovsmose, O. (2006). Kritisk forskning – pædagogisk udforskning. I (Skovsmose og Blomhøj, 2006).

Steinbring, H. (2005). The construction of new mathematical knowledge in classroom interaction: An epistemological perspective (Vol. 38). Springer Science & Business Media. Steinbring, H. (1989). Routine and meaning in the mathematics classroom. For the Learning of Mathematics, 9(1), 24 -33. Tall, D. , 1996: Functions and Calculus. I International handbook of mathematics education, A. J. Bishop et al. (eds. ), 289 -325, Dordrecht, Kluwer, . Tall, D. & Vinner, S. , 1981: Concept image and concept definition in mathematics, with particular reference to limits and continuity. Educational Studies in Mathematics, 12, 151 -169.