LR Parsing Compiler Baojian Hua bjhuaustc edu cn

LR Parsing Compiler Baojian Hua bjhua@ustc. edu. cn

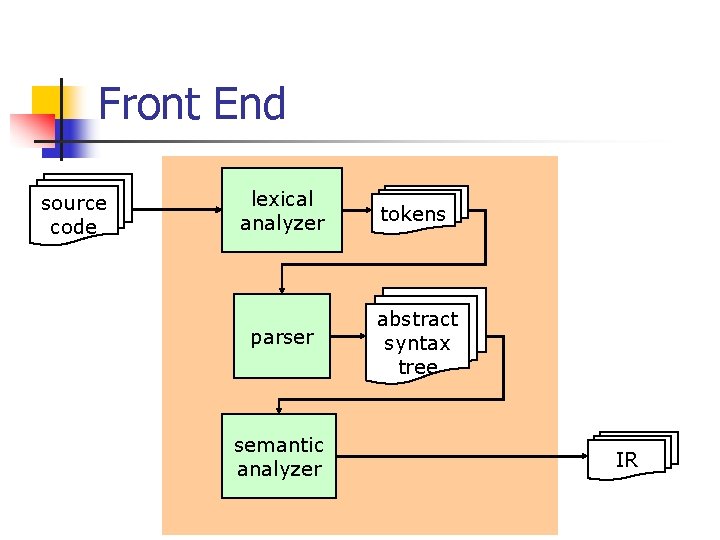
Front End source code lexical analyzer tokens parser abstract syntax tree semantic analyzer IR

Parsing n The parser translates the token sequence into abstract syntax trees n Token sequence: n n abstract syntax trees: n n returned from the lexer compiler internal data structures Must take account of the program syntax

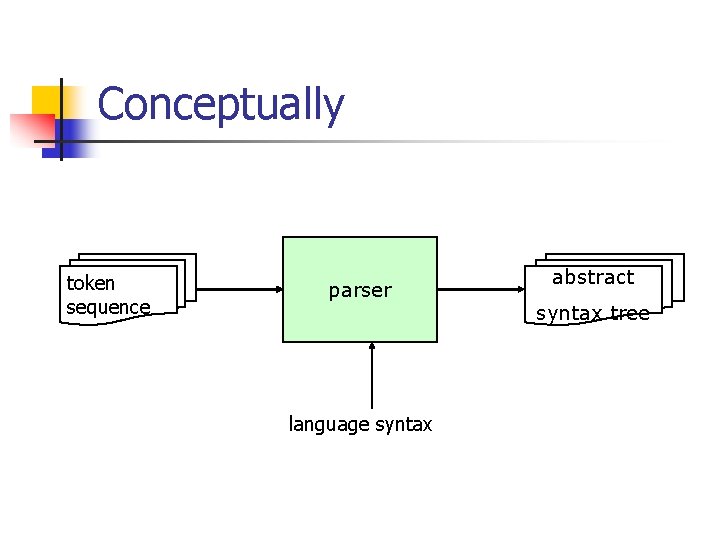
Conceptually token sequence parser language syntax abstract syntax tree

Predicative Parsing n n Grammars encode enough information on how to choose production rules, when input terminals are seen LL(1) pros: n n n simple, easy to implement efficient Cons: n n grammar rewriting ugly

Today’s Topic n Bottom-up Parsing n n a. k. a. shift-reduce parsing, LR parsing This is the predominant algorithm used by automatic YACC-like parser generators n YACC, bison, CUP, C#yacc, etc.

Bottom-up Parsing 1 S : = 2 exp : = term 3 exp : = term 4 term : = factor 5 term : = 6 factor 7 factor exp + 2 + 3 * 4 factor + 3 * 4 term * exp + 3 * 4 exp + factor * 4 factor : = ID : = INT A reverse of rightmost derivation! exp + term * 4 exp + term * factor exp + term exp S

Dot notation n As a convenient notation, we will mark how much of the input we have consumed by using a • symbol exp + 3 * 4 consumed remaining input

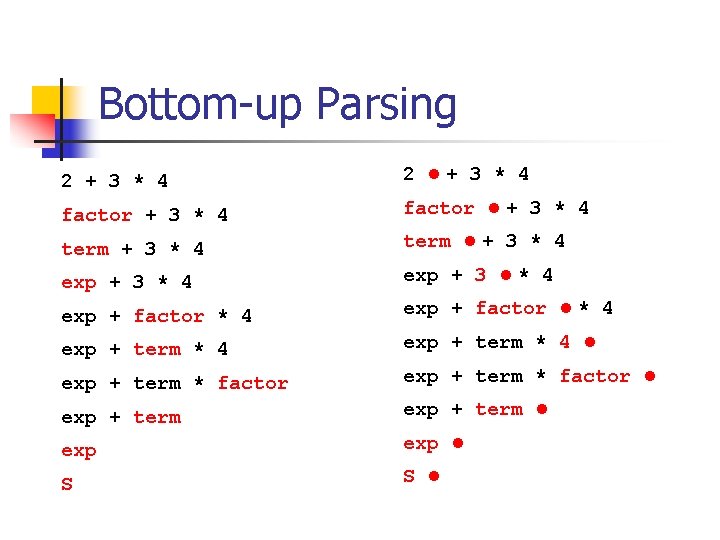
Bottom-up Parsing 2 + 3 * 4 factor + 3 * 4 term + 3 * 4 exp + 3 * 4 exp + factor * 4 exp + term * 4 exp + term * factor exp + term exp S S

Another View 2 + 3 * 4 2 + 3 * 4 factor + 3 * 4 term + 3 * 4 exp + 3 * 4 exp + factor * 4 exp + term * factor exp + term exp S S exp term factor : = : = exp + term * factor ID INT What’s the data structure of the left?

Producing a rightmost derivation in reverse n We do two things: n n n When we reduce by a production A : : = n n n shift a token (terminal) onto the stack, or reduce the top n symbols on the stack by a production is on the top of the stack, pop and push A Key problem: when to shift or reduce?

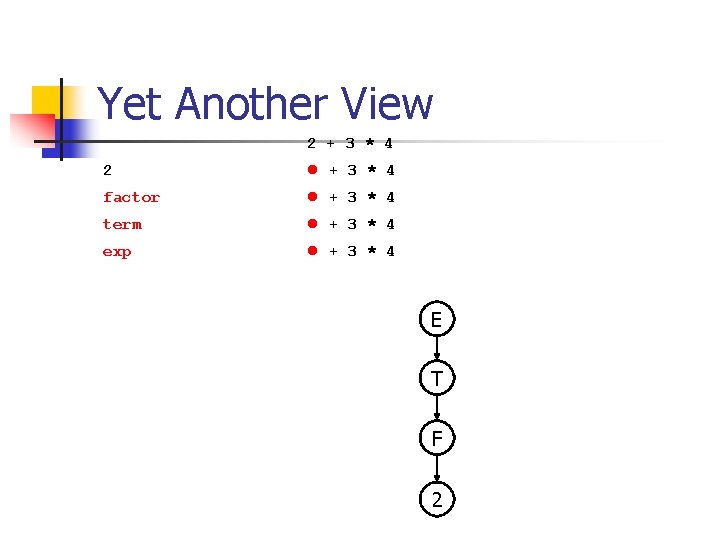
Yet Another View 2 + 3 * 4 2 + 3 * 4 factor + 3 * 4 term + 3 * 4 exp + 3 * 4 E T F 2

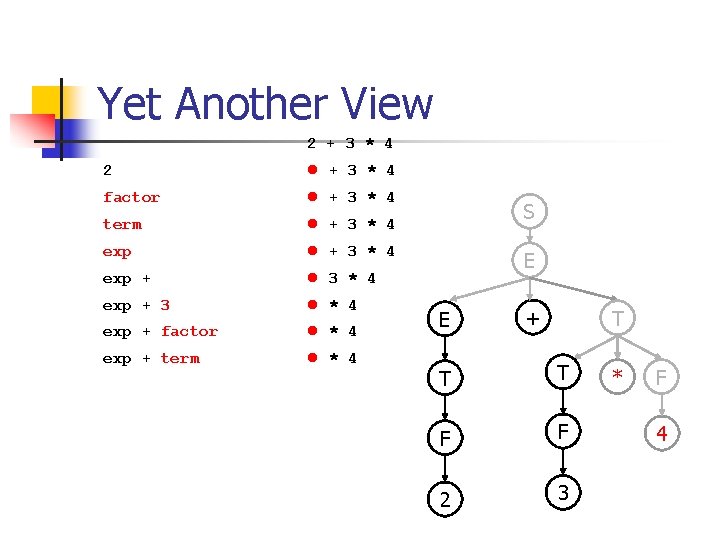
Yet Another View 2 + 3 * 4 2 + 3 * 4 factor + 3 * 4 term + 3 * 4 exp + 3 * 4 exp + factor * 4 exp + term * 4 S E E + T T T F F 2 3 * F 4

A shift-reduce parser n Two components: n n n Stack: holds the viable prefixes Input stream: holds remaining source Four actions: n n shift: push token from input stream onto stack reduce: right-end ( of A : = ) is at top of stack, pop , push A accept: success error: syntax error discovered

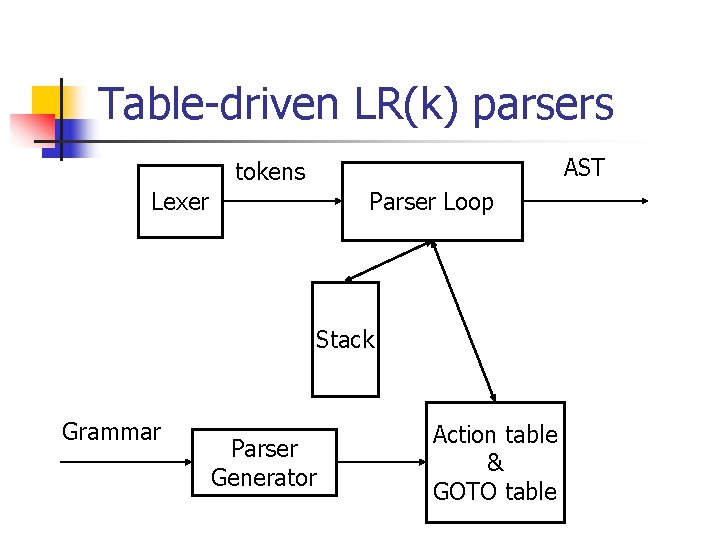
Table-driven LR(k) parsers AST tokens Lexer Parser Loop Stack Grammar Parser Generator Action table & GOTO table

An LR parser n Put S on stack in state s 0 Parser configuration is: n do forever: n (S, s 0, X 1, s 1, X 2, s 2, … Xm, sm; ai ai+1 … an $) n n n read ai. if (action[ai, sm] is shift s then (S, s 0, X 1, s 1, X 2, s 2, … Xm, sm, ai, s; ai+1 … an $) if (action[ai, sm] is reduce A: = then (S, s 0, X 1, s 1, X 2, s 2, … Xm-| |, sm-| |, A, s; ai ai+1 … an $) where s = goto[sm-| |, A] if (action[ai, sm] is accept, DONE if (action[ai, sm] is error, handle error

Generating LR parsers n n n In order to generate an LR parser, we must create the action and GOTO tables Many different ways to do this We will start here by the simplest approach, called LR(0) n Left-to-right parsing, Rightmost derivation, 0 lookahead

Item n n LR(0) items have the form: [production-with-dot] For example, X -> A B C has 4 forms of items n n [X [X : = : = ABC AB C ABC ] ]

What items mean? n [X : = ] n n input is consistent with X : = and we have already recognized [X : = ] n input is consistent with X : = and we can reduce to X

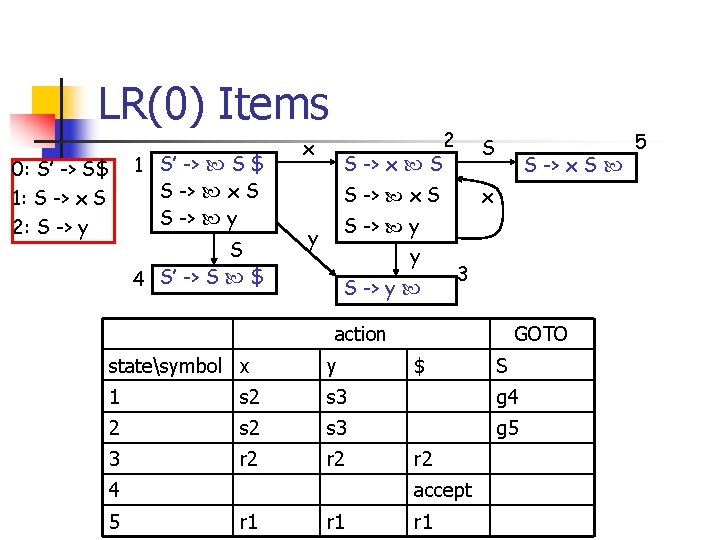
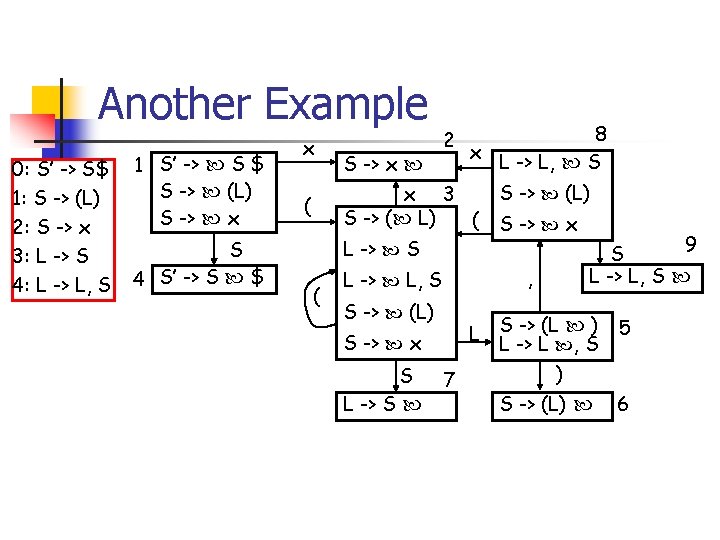
LR(0) Items 1 S’ -> S $ S -> x S S -> y 0: S’ -> S$ 1: S -> x S 2: S -> y S 4 S’ -> S $ x 2 S -> x S S S -> x S -> y y y S -> y S -> x S 3 action GOTO statesymbol x y 1 s 2 s 3 g 4 2 s 3 g 5 3 r 2 4 5 $ r 2 accept r 1 r 1 S 5

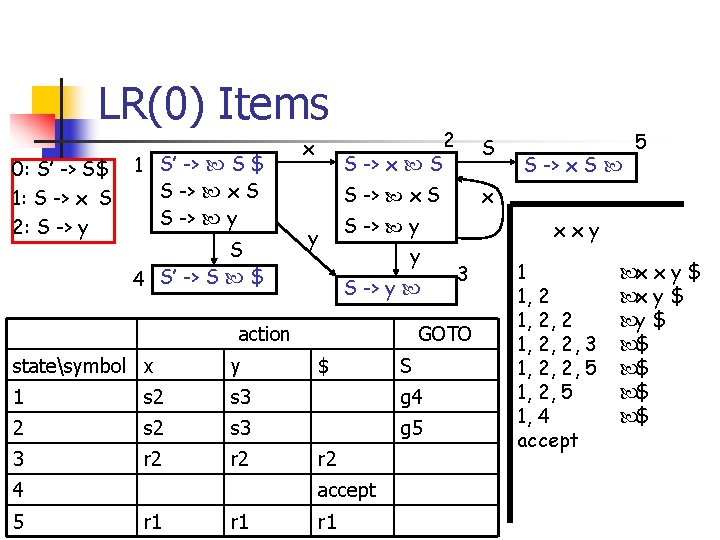
LR(0) Items 0: S’ -> S$ 1: S -> x S 2: S -> y 1 S’ -> S $ S -> x S S -> y S 4 S’ -> S $ x 2 S -> x S S S -> x S -> y y y S -> y action y 1 s 2 s 3 g 4 2 s 3 g 5 3 r 2 4 5 $ r 2 accept r 1 xxy 3 GOTO statesymbol x r 1 S S -> x S 5 1 1, 2, 2, 3 1, 2, 2, 5 1, 4 accept x x y $ y $ $ $

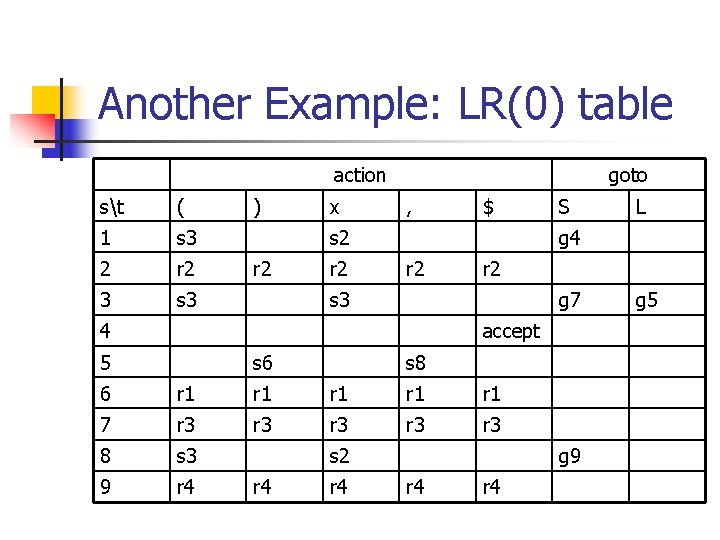
Another Example: LR(0) table action st ( 1 s 3 2 r 2 3 s 3 ) x goto , $ s 2 r 2 S g 4 r 2 s 3 g 7 4 accept 5 s 6 s 8 6 r 1 r 1 r 1 7 r 3 r 3 r 3 8 s 3 9 r 4 s 2 r 4 L g 9 r 4 g 5

LR(0) table construction n Construct LR(0) Items Item Ii becomes state i Parsing actions at state i are: n n n [ A : = a ] Ii and goto(Ii, a) = Ij then action[i, a] = “shift j” [ A : = ] Ii and A S’ then action[i, a] =“reduce by A : = ” [ S’ : = S ] Ii then action[i, $] =“accept”

LR(0) table construction, cont’d n GOTO table for non-terminals: GOTO[i, A] = j if GOTO(Ii, A) = Ij Empty entries are “error” n Table-driven LR-parsing algorithm: n n figure 4. 36 on text

Problems with LR(0) n For every item of the form: X -> n n blindly reduce to X, followed with a “goto” which may not miss any error, but may postpone the detection of some errors n n try “x x y x” on our first example Another problem with LR(0) is that some grammar may have conflicts

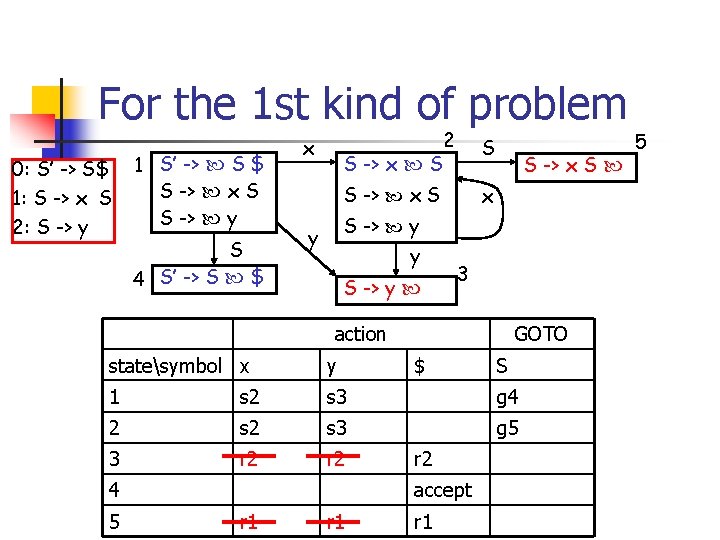
For the 1 st kind of problem 0: S’ -> S$ 1: S -> x S 2: S -> y 1 S’ -> S $ S -> x S S -> y S 4 S’ -> S $ x 2 S -> x S S S -> x S -> y y y S -> y S -> x S 3 action GOTO statesymbol x y 1 s 2 s 3 g 4 2 s 3 g 5 3 r 2 4 5 $ r 2 accept r 1 r 1 S 5

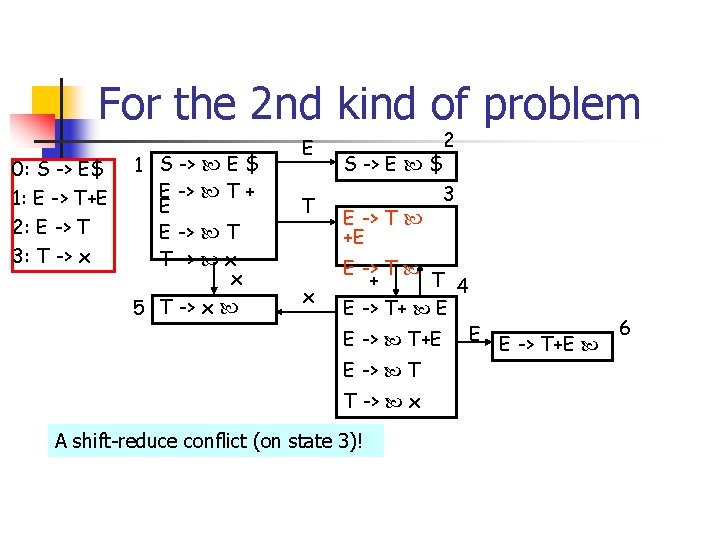
For the 2 nd kind of problem 0: S -> E$ 1: E -> T+E 2: E -> T 3: T -> x 1 S -> E $ E -> T + E E -> T T -> x x 5 T -> x E T x 2 S -> E $ E -> T +E 3 E -> T + T 4 E -> T+ E E -> T+E E E -> T T -> x A shift-reduce conflict (on state 3)! E -> T+E 6

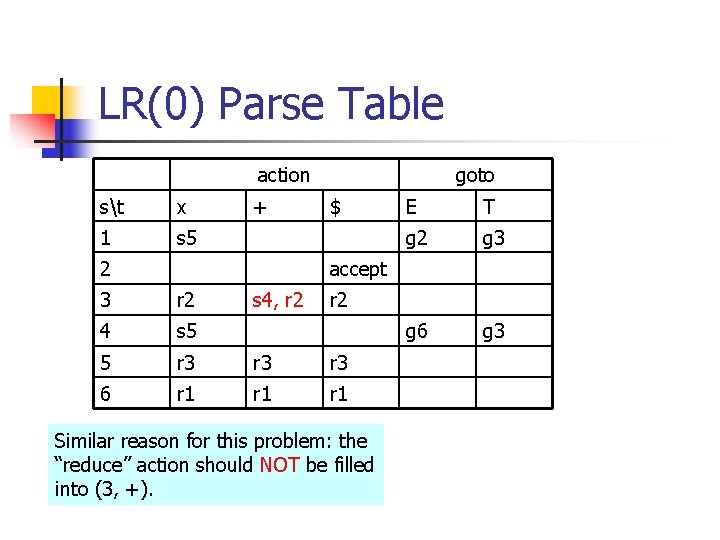
LR(0) Parse Table action st x 1 s 5 + 2 goto $ E T g 2 g 3 g 6 g 3 accept 3 r 2 s 4, r 2 4 s 5 5 r 3 r 3 6 r 1 r 1 Similar reason for this problem: the “reduce” action should NOT be filled into (3, +).

SLR table construction n Construct LR(0) Items Item Ii becomes state i Parsing actions at state i are: n n [ A : = a ] Ii and goto(Ii, a) = Ij then action[i, a] = “shift j” [ A : = ] Ii and A S’ then action[i, a] =“reduce by A : = ” only for all a FOLLOW(A) [ S’ : = S ] Ii then action[i, $] =“accept” GOTO table as before

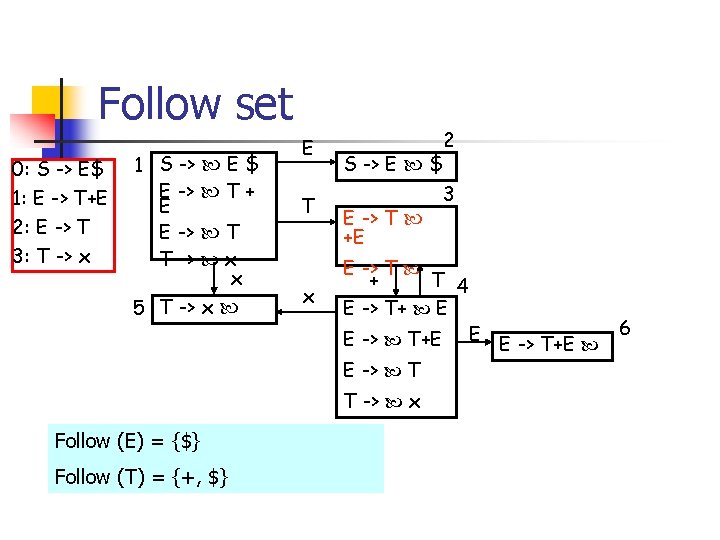
Follow set 0: S -> E$ 1: E -> T+E 2: E -> T 3: T -> x 1 S -> E $ E -> T + E E -> T T -> x x 5 T -> x E T x 2 S -> E $ E -> T +E E -> T + T 4 E -> T+ E E -> T+E E E -> T T -> x Follow (E) = {$} Follow (T) = {+, $} 3 E -> T+E 6

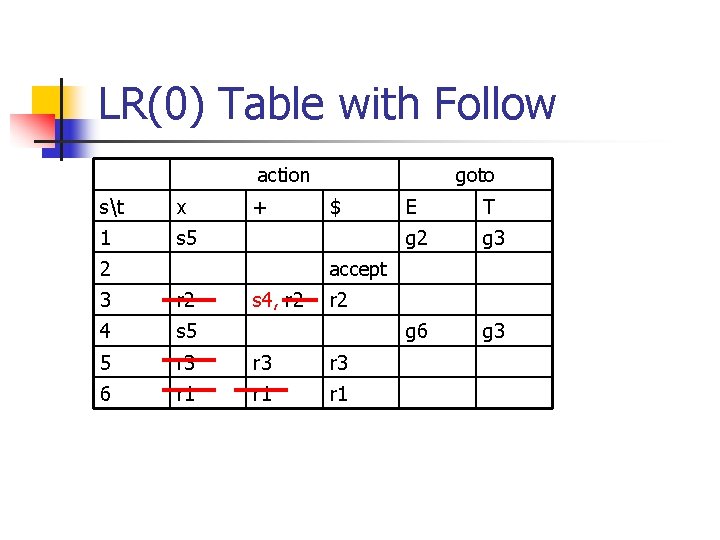
LR(0) Table with Follow action st x 1 s 5 + 2 goto $ E T g 2 g 3 g 6 g 3 accept 3 r 2 s 4, r 2 4 s 5 5 r 3 r 3 6 r 1 r 1

Problems with SLR n For every item of the form: X -> n n n only reduce when the next token tin Follow(X) sometimes, this resolves conflicts such as shift-reduce presented above However, there exist conflicts that can NOT be resolved by SLR

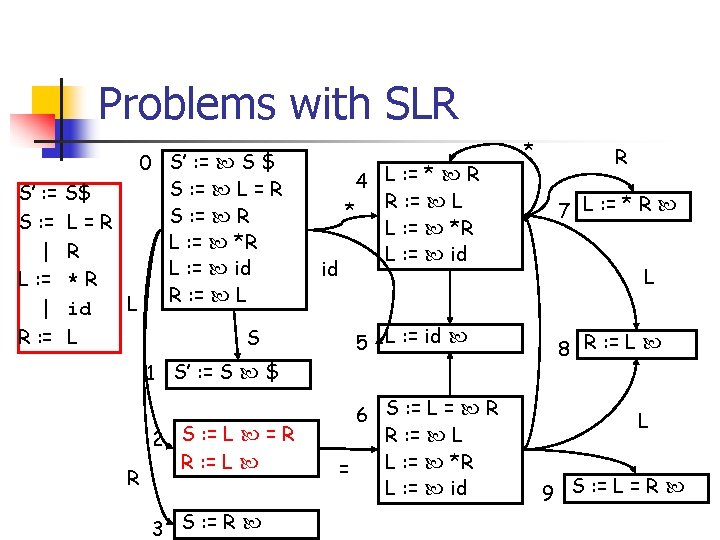
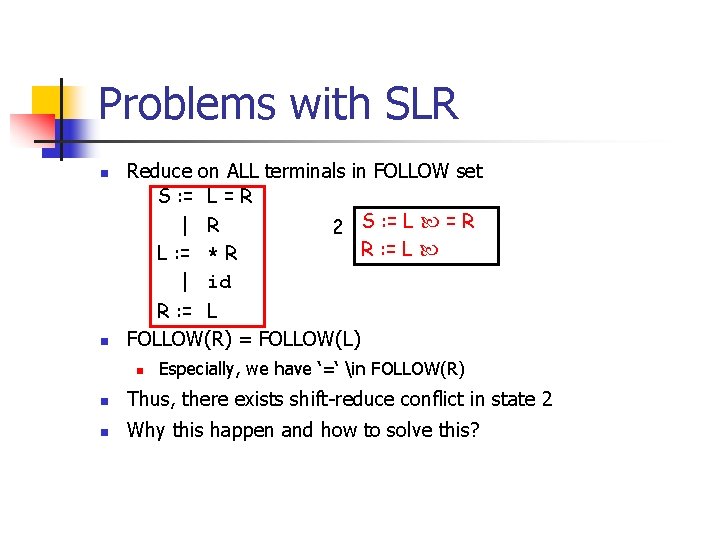
Problems with SLR n n Reduce on ALL terminals in FOLLOW set S : = L = R | R 2 S : = L = R R : = L L : = * R | id R : = L FOLLOW(R) = FOLLOW(L) n Especially, we have ‘=‘ in FOLLOW(R) n Thus, there exists shift-reduce conflict in state 2 n Why this happen and how to solve this?

LR(1) Items n [X : = , a] means n n is at top of stack Input string is derivable from a In other words, when we reduce X : = , a had better be the look ahead symbol. Or, put ‘reduce by X : = ’ in action[s, a] only

LR(1) table construction n n Construct LR(1) Items Item Ii becomes state i Parsing actions at state i are: n [ A : = a , b] Ii and goto(Ii, a) = Ij then action[i, a] = “shift j” n [ A : = , b] Ii and A S’ then action[i, a] =“reduce by A : = ” for b n [ S’ : = S , $] Ii then action[i, $] =“accept” GOTO table as before Initial state is from Item containing [S’ : = S , $]

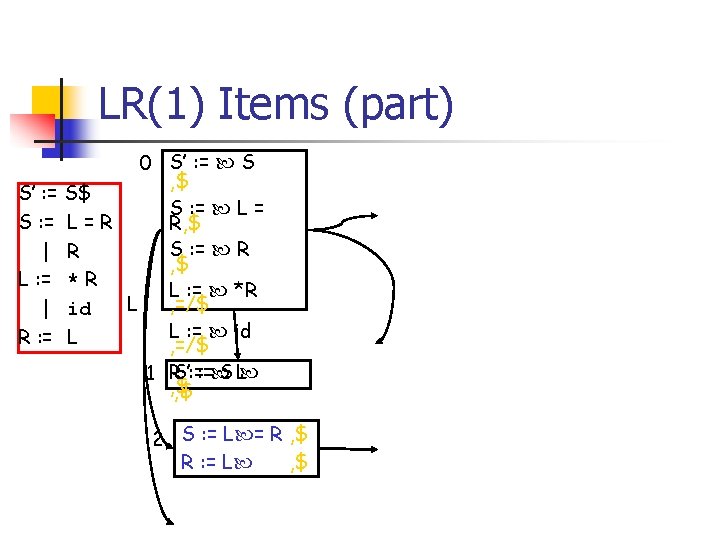
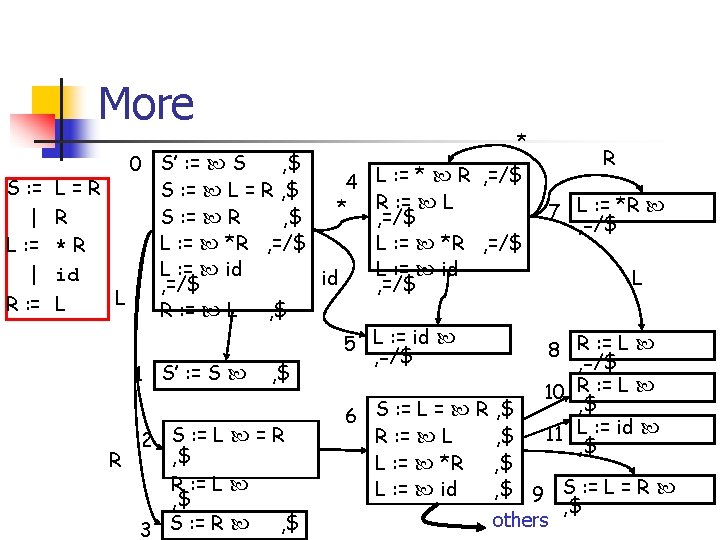
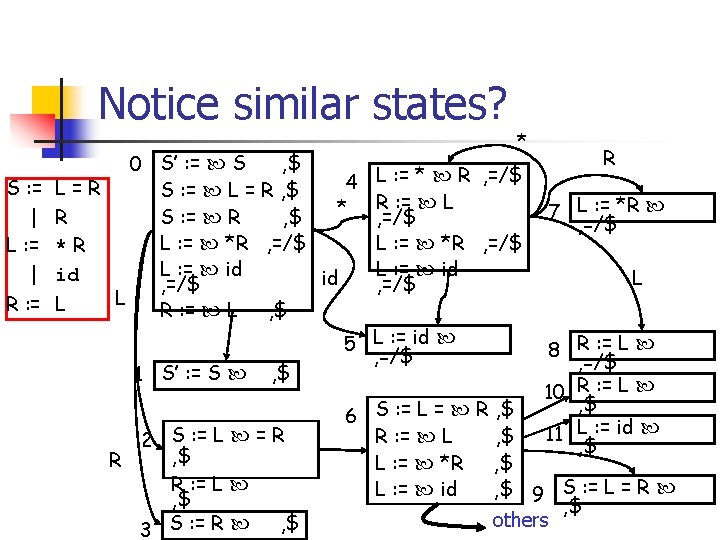
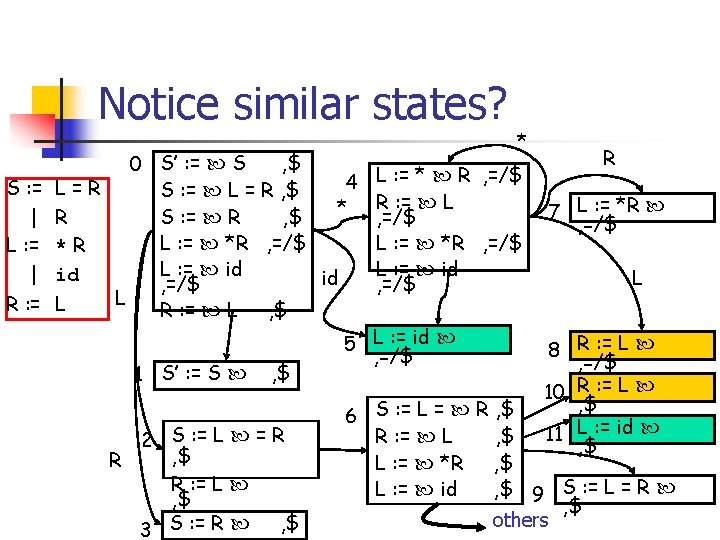
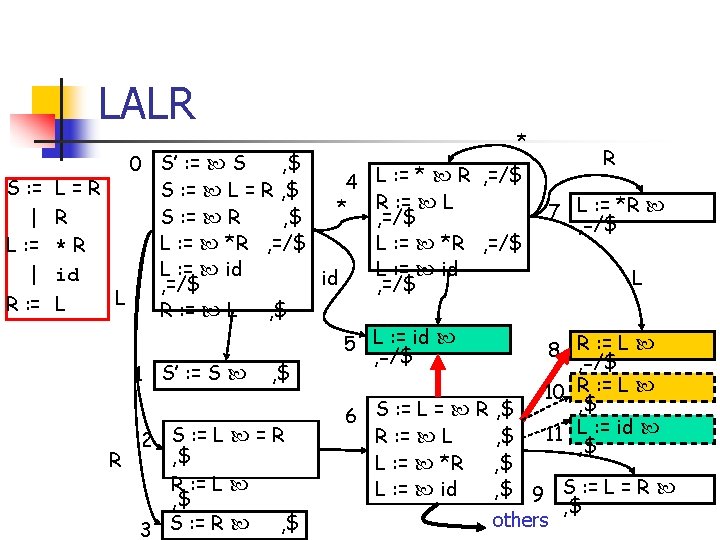
LALR Construction n n Merge items with common cores Change GOTO table to reflect merges Can introduce reduce/reduce conflicts Cannot introduce shift/reduce conflicts

Ambiguous Grammars n No ambiguous grammars can be LR(k) n n hence can not be parsed bottom-up Nevertheless, some of the ambiguous grammar are well-understood, and can be parsed by LR(k) with some tricks n n n precedence associativity dangling-else

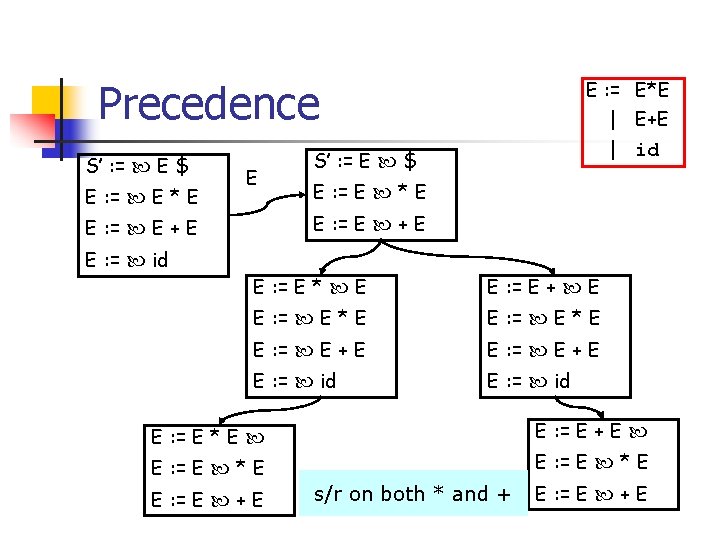
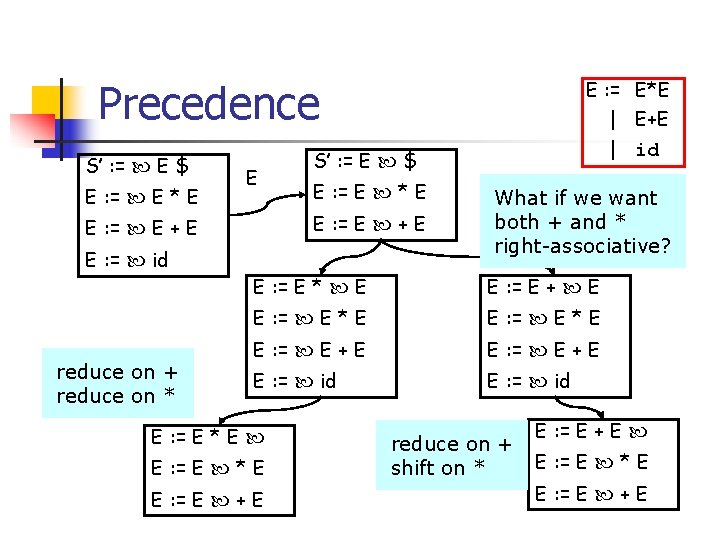
E : = E*E | E+E | id Precedence S’ : = E $ E : = E * E E reduce on + reduce on * E : = E * E E : = E + E E : = E + E E : = id S’ : = E $ What if we want both + and * right-associative? E : = E * E E : = E + E E : = E * E E : = E + E E : = id E : = E * E E : = E * E E : = E + E reduce on + shift on * E : = E + E E : = E * E E : = E + E

Parser Implementation n Implementation Options: n Write a parser by hand, from scratch n n n Use an automatic parser generator n not as boring as writing a lexer recall the dragon compiler Very general & robust. sometimes not quite as efficient as hand-written parsers. good for rapid prototyping. Both are used extensively in production compilers

Yacc Tool semantic analyzer specification parser Yacc Creates a parser from a declarative specification involving a context-free grammar

Brief History n n n YACC stands for Yet Another Compiler It was first developed by Steve Johnson in 1975 for Unix There have been many later versions of YACC (e. g. , GNU Bison), each offering minor improvements Ported to many languages YACC is now a standard tool, defined in IEEE Posix standard P 1003. 2

Yacc User code and Yacc decleartions: declare values available in the rule actions %% Grammar rules: parser specified by CFG rules and associated semantic action that generate abstract syntax %% User code: other code

ML-Yacc Definitions (preliminaries) n Specify type of positions %pos int * int n Specify terminal and nonterminal symbols %term IF | THEN | ELSE | PLUS | MINUS. . . %nonterm prog | exp | stm n Specify end-of-parse token %eop EOF n Specify start symbol (by default, non terminal in LHS of first rule) %start prog

Example %% %term ASSIGN | ID | PLUS |NUM | SEMICOLON | TIMES %nonterm s | e %pos int %start p %eop EOF %left PLUS %left TIMES %% p -> -> s -> e -> | | | s SEMICOLON p () () ID ASSIGN e () e PLUS e () e TIMES e () ID () NUM ()

Summary n Bottom-up parsing n n reverse order of derivations LR grammars are more powerful n n n use of stacks and parse tables yet more complex Bonus: tools do the hard work for you, read the online Yacc manual