LPP Simplex Method Simplex method Introduction Simplex method

Simplex method Introduction – �Simplex method through an iterative process progressively approaches and ultimately

Ø Basic terms 1. Standard form. All constraints are written as equalities. 2. Slack

6. Zj Row. Represents total contribution of outgoing profit when one unit of non

Q- A plant is engaged in production of 2 products which are processed through

Ø Solution- Max Z = 60 A + 40 B Subject to Constraints 7

Cj 60 40 0 Minimum ratio CB Basic variable Solution values A B(=Xb) B

�Working notes� 1. Zj (for A )= 0*7 + 0*8 + 0*15 = 0

�Since 60 is highest vertically , it becomes pivot column, and we divide pivot

Cj 60 40 0 CB Basic Solution variable values B(=Xb) A B S 1

�Now we replace the s 3 column 0, 0, 1 with A in table

�For b row wise- (8 -7 i. e-B-A from table 1) &(16/15 from table

�Now for Zj= table 2 Cb*A = 0*0 + 60*1 = 60 Cb* B

Slides: 14

Download presentation

LPP : Simplex Method

Simplex method Introduction – �Simplex method through an iterative process progressively approaches and ultimately reaches to the maximum or minimum values of the objective function. �Helps the decision maker to identify unbounded solution, multiple solution and infeasible problem Definition“Simplex method is suitable for solving linear programming problems with a larger number of variables. ”

Ø Basic terms 1. Standard form. All constraints are written as equalities. 2. Slack variable. A variable added to the left hand side of a less than or equal to constraint to convert the constraint into an equality. 3. Surplus variable. Variable subtracted from the left hand side of the greater than or equal to constraint, to convert the constraint into an equality. 4. Basic solutions. A solution obtained by setting(n-m) variables equal to zero and solving for remaining m variables. 5. Optimal solution. Any basic feasible solution which optimizes(minimizes or maximizes)the objective function of general L. P problem is called optimal solution.

6. Zj Row. Represents total contribution of outgoing profit when one unit of non basic variable is introduced into the basis variable place. 7. Cj-Zj(or Net Evaluation or Index)Row. The row containing net profit(or net loss)that will result from introducing one unit of the variable indicated in that column in the solution. 8. Pivot column. The column with largest positive number(maximization) or largest negative number(minimization)in the net evaluation row. 9. Pivot row. The row corresponding to the variable that will leave the basis in order to make room for the variable entering. smallest positive ratio.

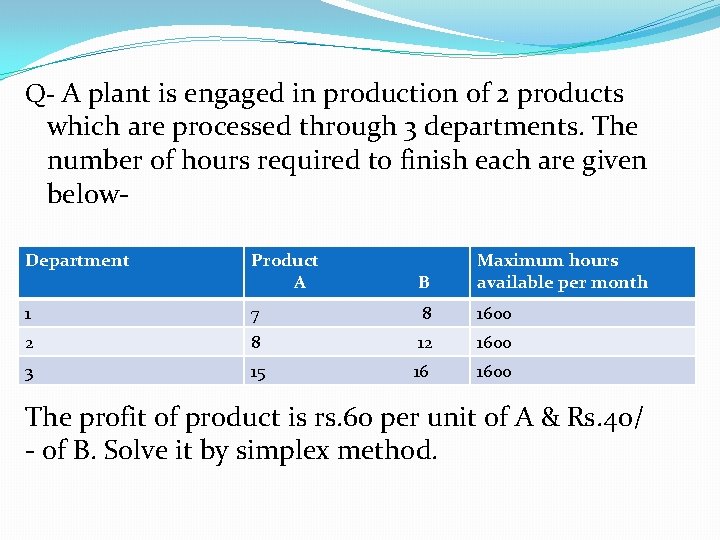
Q- A plant is engaged in production of 2 products which are processed through 3 departments. The number of hours required to finish each are given below- Department Product A B Maximum hours available per month 1 7 8 1600 2 8 12 1600 3 15 16 1600 The profit of product is rs. 60 per unit of A & Rs. 40/ - of B. Solve it by simplex method.

Ø Solution- Max Z = 60 A + 40 B Subject to Constraints 7 A + 8 B ≤ 1600 8 A+ 12 B ≤ 1600 15 A + 16 B ≤ 1600 A, B ≥ 0 Z = 60 A + 40 B + 0 S 1 + 0 S 2 + 0 S 3 7 A+ 8 B+ S 1+ 0 S 2+ 0 S 3= 1600 8 A+ 12 B+ 0 S 1+ S 2+ 0 S 3= 1600 15 A+ 16 B+ 0 S 1 + 0 S 2+ S 3= 1600 A, B, S 1, S 2, S 3 ≥ 0

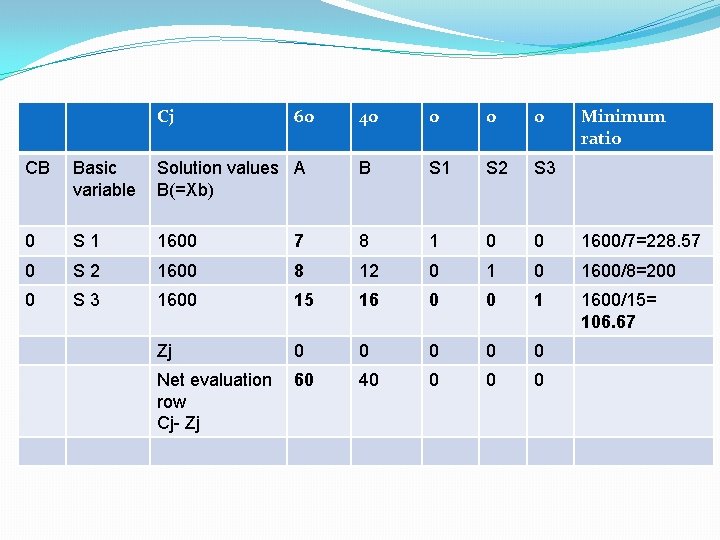
Cj 60 40 0 Minimum ratio CB Basic variable Solution values A B(=Xb) B S 1 S 2 S 3 0 S 1 1600 7 8 1 0 0 1600/7=228. 57 0 S 2 1600 8 12 0 1600/8=200 0 S 3 1600 15 16 0 0 1 1600/15= 106. 67 Zj 0 0 0 Net evaluation row Cj- Zj 60 40 0

�Working notes� 1. Zj (for A )= 0*7 + 0*8 + 0*15 = 0 (A*CB) (for B)= 0*8 + 0*12 + 0*16 = 0 (B*CB) (for S 1)=0*1+ 0*0 = 0 (S 1*CB) same for S 2 & S 3. � 2. Net evaluation row- Cj- Zj= A= 60 -0 =6 B= 40 -0=40 S 1= 0 -0=0 S 2= 0 -0=0 S 3= 0 -0=0

�Since 60 is highest vertically , it becomes pivot column, and we divide pivot column to CJ to get minimum ratios. �Here the minimum is 106. 67 row wise, so that row gets out.

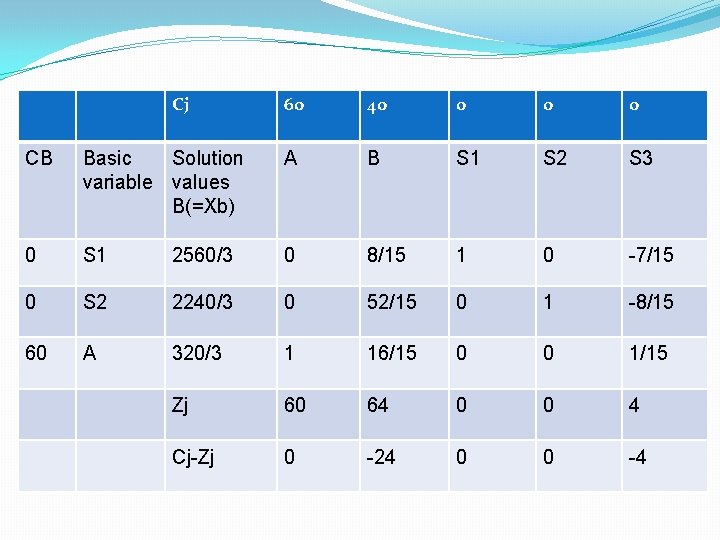
Cj 60 40 0 CB Basic Solution variable values B(=Xb) A B S 1 S 2 S 3 0 S 1 2560/3 0 8/15 1 0 -7/15 0 S 2 2240/3 0 52/15 0 1 -8/15 60 A 320/3 1 16/15 0 0 1/15 Zj 60 64 0 0 4 Cj-Zj 0 -24 0 0 -4

�Now we replace the s 3 column 0, 0, 1 with A in table 2. �To make 15 to 1, we have to divide 15 to whole “row”. Cj = 1600/15= i. e 320/3 A =15/15= 1 B=16/15 S 1 =0/15=0 S 2 =0/15=0 S 3 =1/15 Now for S 1 row=(consider the first and second table values) 1600 -7 *320 = 1600*3 - 7*320 = 4800 – 2240 =2560 3 3 3 �Now for S 2 row= 1600 -8*320 = 1600*3 - 8*320 = 4800 -2560 = 2240 3 3 3

�For b row wise- (8 -7 i. e-B-A from table 1) &(16/15 from table 2) 8 - 7*16 =`15*8 – 7*16 = 120 -112 = 8 15 15 � For S 212 - 8*16 = 180 -128 = 52 15 15 15 �Now, �For s 3=(0 -7 i. e- s 3 -A from table 1)&(1/15 we got from slide form slide 11) 0 - 7*1 = 15*0 -7 = -7 15 15 0 - 8* 1 = -8 15 15

�Now for Zj= table 2 Cb*A = 0*0 + 60*1 = 60 Cb* B = 0* 8/15 + 0*52/15 + 60*16/15 = 64 S 1= 0*1 + 0*0 + 60*0 = 0. same for S 2 S 3= 0* -7/15 + 0*- 8/15 + 60*1/15 = 4 Cj- zj = A= 60 -60=0 B = 40 -64 = -24 S 1 = 0 - 0 =0 , same for s 2 s 3= 0 - 4= -4 , , since all cj-zj appears in negative and zero, solution is optimal. so, �Max Z = 60 A + 40 B � =60(320/3) + 40 (0) � = 6400